Solution des exercices : Introduction à la géométrie - Le plan et ses parties - 6e
Classe:
Sixième
Exercice 1
Donnons un objet qui à la forme :
$-\ $ D'un parallélépipède rectangle : paquet de sucre en morceaux

$-\ $ D'un cube : dés cubiques

$-\ $ D'un cylindre : pot de lait

$-\ $ D'une sphère : ballon de basket

Exercice 2
1) Marquons deux points $A\ $ et $\ C$ puis traçons la droite $(AC)$ avec la règle.
2) Marquons le point $M$ tel que $M$ n'appartient pas à la droite $(AC).$
3) Traçons les droites $(AM)\ $ et $\ (CM).$
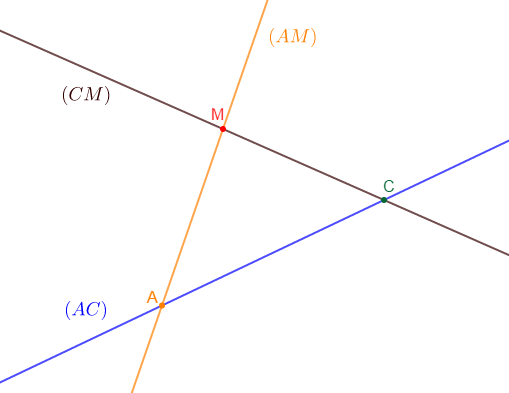
4) Nommons les demi-droites d'extrémité $M.$
Les demi-droites d'extrémité $M$ sont :
$$[AM)\;,\ [CM)\;,\ [MC)\quad\text{et}\quad [MA)$$
5) Nommons tous les segments.
Les segments obtenus sont :
$$[AM]\;,\ [CM]\quad\text{et}\quad[AC]$$
On peut aussi les noter par :
$[MA]\;,\ [MC]\ $ et $\ [CA]$
Exercice 3
1) Reproduisons la figure
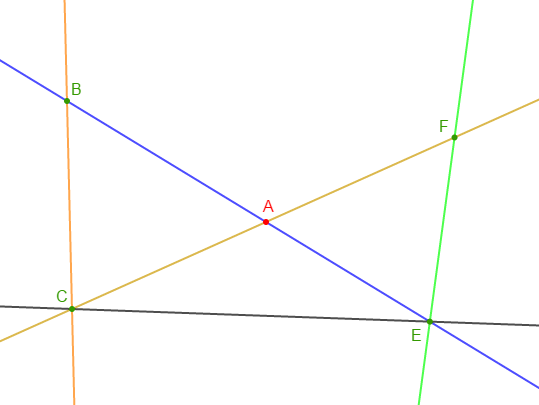
2) Complétons les pointillés par $\in$ ou $\notin .$
$$A\in(BE)\;;\quad A\notin(CE)\;;\quad B\notin(AC)\;;\quad B\in(AE)$$
La droite $(BE)$ passe par le pont $A$ donc, $A\in(BE)$
Le point $A$ n'est pas sur la droite $(CE)$ donc, $A\notin(CE)$
Comme la droite $(AC)$ ne passe pas par $B$ alors, $B\notin(AC)$
La droite $(AE)$ passe par le pont $B$ donc, on peut dire $B\in(AE)$
3) On constate que les droites $(BE)\ $ et $\ (CF)$ se coupent au point $A.$
Donc, on peut dire que $A$ est le point de rencontre ou encore le point d'intersection des droites $(BE)\ $ et $\ (CF)$
4) Traçons les droites $(BC)\ $ et $\ (EF).$
Exercice 4
1) Marquons les points $A\;,\ B\ $ et $\ E$ sur une droite $(d).$
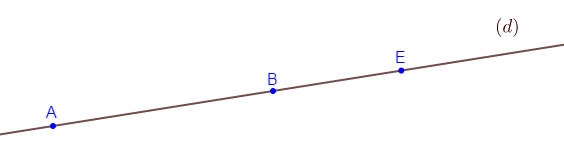
2) a) Deux autres noms de la droite $(d)$ sont :
$$(AB)\ \text{ et }\ (AE)$$
b) Les demi-droites d'origine $B$ sont :
$$[BA)\ \text{ et }\ [BE)$$
3) Nommons tous les segments qui sont sur la figure.
$$[AB]\;,\ [BE]\ \text{ et }\ [AE]$$
Exercice 5
1) Marquons les points $A\;,\ B\ $ et $\ E$ sur une droite $(d).$
2) Marquons un point $F$ tel que : $F\notin\;(d).$
3) Traçons les droites $(AF)\;,\ (BF)\ $ et $\ (EF).$
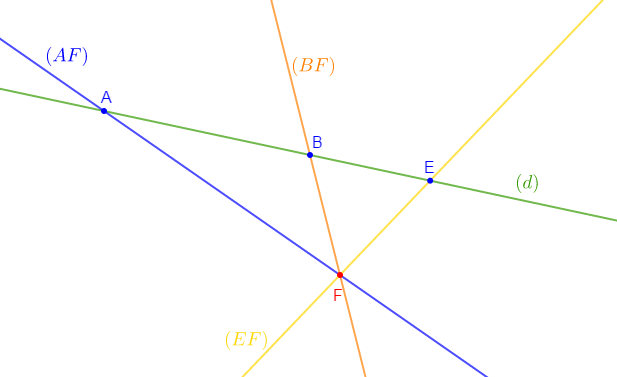
4) Déterminons les points d'intersections des droites
a) $(AF)\ $ et $\ (EF)$
Les droites $(AF)\ $ et $\ (EF)$ se coupent en $F$ donc, $F$ est le point d'intersection des droites $(AF)\ $ et $\ (EF)$
b) $(BF)\ $ et $\ (AE)$
Comme les droites $(BF)\ $ et $\ (AE)$ se coupent en $B$ alors, $B$ est le point d'intersection des droites $(BF)\ $ et $\ (AE)$
5) Nommons tous les segments
$$[AF]\;,\ [AB]\;,\ [AE]\;,\ [BE]\;,\ [BF]\;,\ [EF]$$
Exercice 6
1) Construisons quatre points alignés $M\;,\ N\;,\ P\ $ et $\ Q$ sur une droite $(d)$ dans cet ordre.
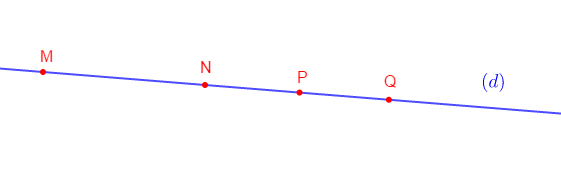
2) Trois autres noms de la droite $(d)$ sont :
$$(MN)\;,\ (NP)\;,\ (PQ)$$
3) Les demi-droites d'origine $P$ sont :
$$[PM)\;,\ [PN)\;,\ [PQ)$$
4) Nommons quatre segments dans cette figure.
$$[MN]\;,\ [MP]\;,\ [NQ]\;,\ [PQ]$$


Exercice 11
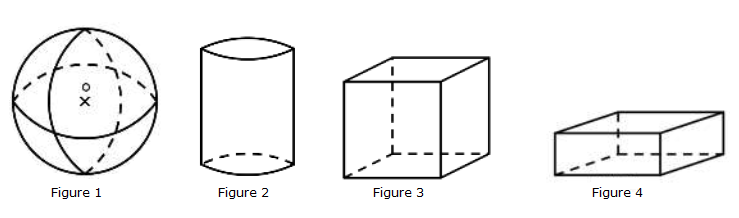
Donnons le nom de chacune des figures ci-dessous :

$-\ $ Figure $1$ : une sphère
$-\ $ Figure $2$ : un cylindre
$-\ $ Figure $3$ : un cube
$-\ $ Figure $4$ : un parallélépipède rectangle
Exercice 12
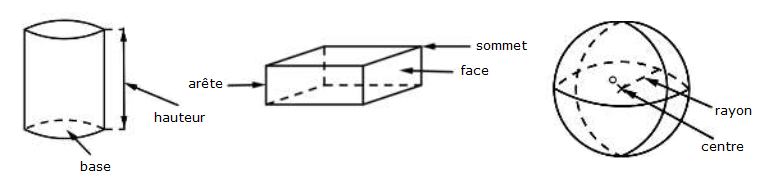
Reproduisons chacune des figures ci-dessous, puis écrivons pour chaque flèche le nom correspondant à la partie désignée.

Exercice 13
Pour chaque énoncé, écrivons le numéro puis choisissons la bonne réponse.
$$\begin{array}{|l|c|c|c|}\hline\qquad\qquad\text{Enoncés}&\text{Réponse A}&\text{Réponse B}&\text{Réponse C}\\\hline\text{1. Le nombre d'arêtes}&6&8&12\\\quad \text{d'un parallélépipède est}&&&\\\hline\text{2. Le nombre de sommets}&6&8&12\\\quad \text{d'un cube est}&&&\\\hline\text{3. Le nombre de faces}&6&8&12\\\quad \text{d'un parallélépipède est}&&&\\\hline\text{4. Un parallélépipède a pour face}&\text{un carré}&\text{un losange}&\text{un rectangle}\\\hline\end{array}$$
Nous obtenons alors les correspondances suivantes :
$$\begin{array}{rcl} 1.&\longleftrightarrow&\text{Réponse C}\\\\2.&\longleftrightarrow&\text{Réponse B}\\\\3.&\longleftrightarrow&\text{Réponse A}\\\\4.&\longleftrightarrow&\text{Réponse C}\end{array}$$
Ce qui donne donc :
1. Le nombre d'arêtes d'un parallélépipède est : $12$
2. Le nombre de sommets d'un cube est : $8$
3. Le nombre de faces d'un parallélépipède est : $6$
4. Un parallélépipède a pour face un rectangle
Exercice 14
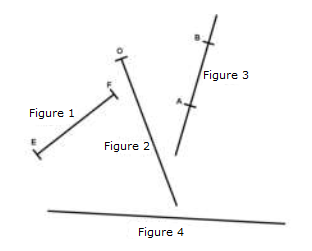
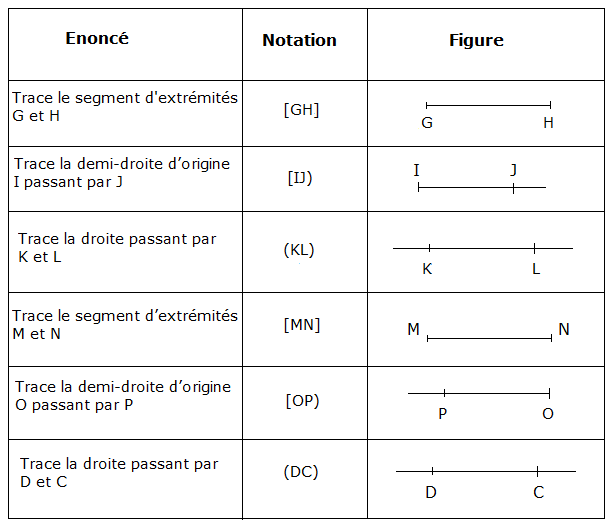
On donne les figures ci-dessous. Pour chaque figure, recopions le numéro et indiquons s'il s'agit d'une droite, d'une demi-droite ou d'un segment.

$-\ $ Figure $1$ : une segment
$-\ $ Figure $2$ : une demi-droite
$-\ $ Figure $3$ : une droite
$-\ $ Figure $4$ : une droite
Exercice 15
Recopions puis complétons les phrases ci-dessous avec les mots :
droite, demi-droite, segment, origine, extrémités ou points.
$[AB]$ est un segment ; les points $A\ $ et $\ B$ sont ses extrémités.
$(CD)$ est une droite ; elle passe par les points $C\ $ et $\ D.$
$[EF)$ est une demi-droite ; le point $E$ est son origine.
Exercice 16
1) Par un point donné, il passe une infinité de droites
2) Par deux points distincts, il passe une et une seule droite
Exercice 17
1) Reproduisons puis complétons le tableau suivant :

2) Reproduisons puis complétons le tableau suivant :

Exercice 22
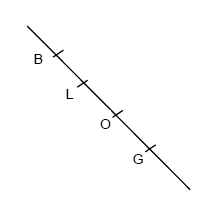
On considère la figure ci-dessous. Les points $B\;,\ L\;,\ O\ $ et $\ G$ sont alignés.

Recopions et complétons par $\in$ ou par $\notin$
$O\in[BG]\quad O\notin[BL]\quad O\in[GL]$
$G\in[LO)\quad G\notin[OL)\quad G\in[BL)$
$L\in[GO)\quad L\notin[GO]\quad G\in(LO)$
Exercice 23
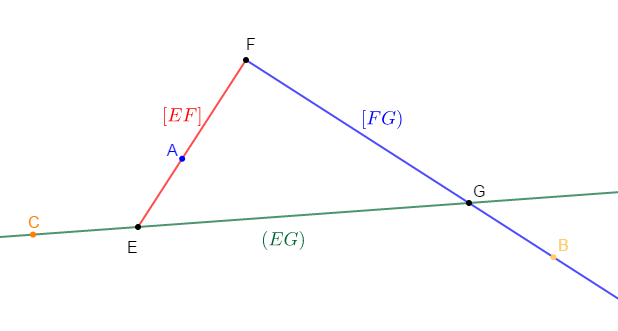
1) Plaçons trois points $E\;,\ F\ $ et $\ G$ non alignés.
2. a) Traçons le segment $[EF]$ en rouge.
b) Traçons la demi-droite $[FG)$ en bleu.
c) Traçons la droite $(EG)$ en vert.
3) Plaçons un point $A$ tel que $A\in[EF].$
4) Plaçons un point $B$ tel que $B\in[FG)\;,\ B\notin [FG].$
$B$ est donc sur la demi-droite $[FG)$ mais hors du segment $[FG]$
5) Plaçons un $C$ point tels que $C\in(EG)\;,\ C\notin[EG).$
$C$ n'est pas donc sur la demi-droite $[EG)$ mais il est sur l'autre partie de la droite $(EG)$

Exercice 24
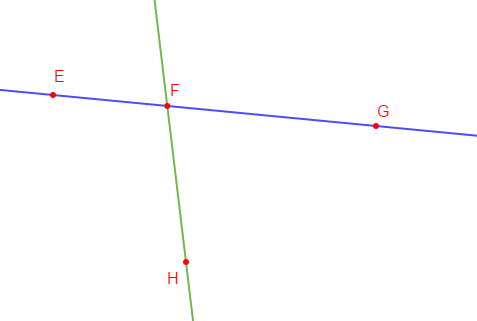
1) Plaçons quatre points $E\;,\ F\;,\ G\ $ et $\ H$ tels que :
$\centerdot\ \ E\;,\ F\ $ et $\ G$ soient alignés dans cet ordre ;
$\centerdot\ \ E\;,\ F\ $ et $\ H$ ne soient pas alignés.

2) En utilisant les symboles $\in$ ou $\notin$ recopions et complétons
$E\in(FG)\quad E\in[EF]\quad E\notin[FG]\quad E\in[EG)$
$F\in[EG)\quad H\notin(FG)\quad H\in[FH]\quad G\in[FG).$
Exercice 25
On donne la figure ci-dessous

1) Remplaçons les pointillés par $\in$ ou $\notin$
$A\in(xy)\quad B\in(AE)\quad E\in(AB)\quad A\in(AB)$
$B\in[AE)\quad E\notin[CB]\quad A\notin[CB]\quad B\notin[CE)$
$A\in[EB)\quad C\in[EA]\quad H\notin(D)$
2) Trois noms de la droite $(xy)$ sont :
$$(AB)\;,\ (AE)\;,\ (BC)$$
3) Les noms de la demi- droite $[BE)$ sont :
$$[BC)\;,\ [BE)\;,\ [By)$$
Exercice 28
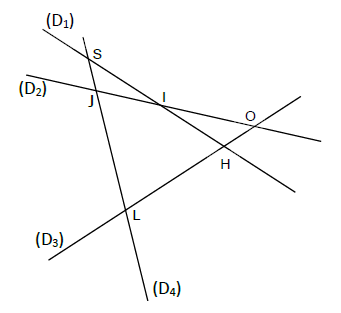
A l'aide de la figure ci-dessous complétons :

$-\ $ les droite $(D_{1})\ $ et $\ (D_{2})$ se coupent en $I$
$-\ \ I$ est le point d'intersection des droites $(D_{1})\ $ et $\ (D_{2})$
$-\ $ les droites $(IJ)\ $ et $\ (OL)$ sont sécantes en $O$
$-\ $ les droites $(D_{4})\ $ et $\ (OH)$ se coupent en $L$
$-\ \ H$ est le point d'intersection des droites $(LH)\ $ et $\ (SI)$
Exercice 29
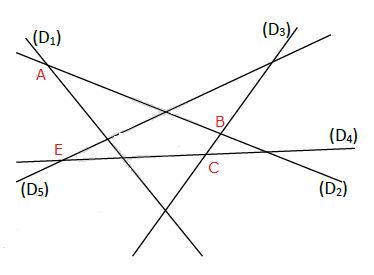
Reproduisons la figure ci-dessous.
$A$ est le point d'intersection de $(D_{1})\ $ et $\ (D_{2}).$
Les droites $(D_{2})\ $ et $\ (D_{3})$ se coupent en $B.$
Les droites $(D_{4})\ $ et $\ (D_{3})$ se coupent en $C.$
Les droites $(D_{4})\ $ et $\ (D_{5})$ se coupent en $E.$
Plaçons les points $A\;,\ B\;,\ C\ $ et $\ E.$

Auteur:
Diny Faye

Commentaires
(non vérifié)
mer, 11/08/2023 - 21:06
Permalien
mais ça ne serait pas de la
Eleve (non vérifié)
mer, 11/08/2023 - 21:07
Permalien
Merci ça aide
Eleve (non vérifié)
mer, 11/08/2023 - 21:07
Permalien
Merci ça aide
Diariatou (non vérifié)
ven, 11/10/2023 - 21:06
Permalien
C'est une très bonne
Anonyme (non vérifié)
jeu, 11/20/2025 - 17:22
Permalien
Wallahi est une très bonne
Ajouter un commentaire