Théorème de Thalès - 3e
Classe:
Troisième
I. Activité
Soient $(\Delta)$ et $(\Delta')$ deux droites sécantes en $O$, $A\;,\ B$ et $C$ trois points de $(\Delta)$ et $A'\;,\ B'$ et $C'$ trois points de $(\Delta')$ tels que $(AA')\parallel(BB')\parallel(CC').$
Soient $I\;,\ J$ et $K$ les projetés orthogonaux respectifs du point $O$ sur les droites $(AA')\;,\ (BB')$ et $(CC').$
a) Démontrer que $\widehat{OAI}=\widehat{OBJ}=\widehat{OCK}$ et $\widehat{OA'I}=\widehat{OB'J}=\widehat{OC'K}$
b) Calculer $\sin\widehat{OAI}\;,\ \sin\widehat{OBJ}\;,\ \sin\widehat{OA'I}$ et $\sin\widehat{OB'J}$
Démontrer que $\dfrac{OA}{OB}=\dfrac{OA'}{OB'}$
En déduire que $\dfrac{OA}{OC}=\dfrac{OA'}{OC'}$ et $\dfrac{OB}{OC}=\dfrac{OB'}{OC'}$
c) Démontrer que $\dfrac{AB}{AC}=\dfrac{A'B'}{A'C'}\;;\ \dfrac{AB}{BC}=\dfrac{A'B'}{B'C'}\;;\ \dfrac{BC}{AC}=\dfrac{B'C'}{A'C'}$
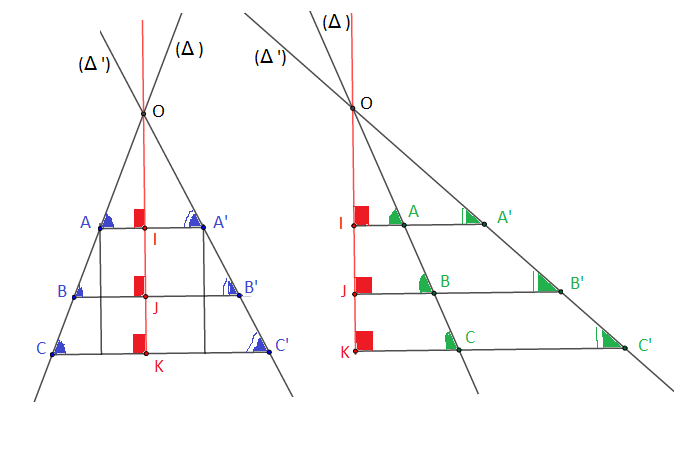
a) Démontrons que $\widehat{OAI}=\widehat{OBJ}=\widehat{OCK}$ et $\widehat{OA'I}=\widehat{OB'J}=\widehat{OC'K}$
On a : $(AA')\parallel(BB')\;;\ (\Delta)\cap(AA')=A$ et $(\Delta)\cap(BB')=B$
Alors, $\widehat{OAA'}=\widehat{OBB'}$
Or, $\widehat{OAA'}=\widehat{OAI}$ et $\widehat{OBB'}=\widehat{OBJ}$
Donc, $\widehat{OAI}=\widehat{OBJ}$
De même on aura : $\widehat{OAI}=\widehat{OCK}$
D'où, $\widehat{OAI}=\widehat{OBJ}=\widehat{OCK}$
De manière alignée on aura : $\widehat{OA'I}=\widehat{OB'J}=\widehat{OC'K}$
b) On a : $\sin\widehat{OAI}=\dfrac{OI}{OA}\;,\ \sin\widehat{OBJ}=\dfrac{OJ}{OB}\;,\ \sin\widehat{OA'I}=\dfrac{OI}{OA'}$ et $\sin\widehat{OB'J}=\dfrac{OJ}{OB'}$
Démontrons que $\dfrac{OA}{OB}=\dfrac{OA'}{OB'}$
On a : $\sin\widehat{OAI}=\dfrac{OI}{OA}\;,\ \sin\widehat{OBJ}=\dfrac{OJ}{OB}$ et $\widehat{OAI}=\widehat{OBJ}$
Alors, $\dfrac{OI}{OA}=\dfrac{OJ}{OB}$
Donc, $\dfrac{OI}{OJ}=\dfrac{OA}{OB}$
De même on a : $\sin\widehat{OA'I}=\dfrac{OI}{OA'}\;,\ \sin\widehat{OB'J}=\dfrac{OJ}{OB'}$ et $\widehat{OA'I}=\widehat{OB'J}$
Alors, $\dfrac{OI}{OA'}=\dfrac{OJ}{OB'}$
Donc, $\dfrac{OI}{OJ}=\dfrac{OA'}{OB'}$
D'où, $$\boxed{\dfrac{OA}{OB}=\dfrac{OA'}{OB'}}$$
Déduisons que $\dfrac{OA}{OC}=\dfrac{OA'}{OC'}$ et $\dfrac{OB}{OC}=\dfrac{OB'}{OC'}$
Par analogie à la démonstration de $\dfrac{OA}{OB}=\dfrac{OA'}{OB'}$
on aura : $$\boxed{\dfrac{OA}{OC}=\dfrac{OA'}{OC'}\;\text{ et }\;\dfrac{OB}{OC}=\dfrac{OB'}{OC'}}$$
c) Démontrons que $\dfrac{AB}{AC}=\dfrac{A'B'}{A'C'}$
On a : $\sin\widehat{ABJ}=\dfrac{IJ}{AB}\;,\ \sin\widehat{ACK}=\dfrac{IK}{AC}$ et $\widehat{ABJ}=\widehat{ACK}$
Alors, $\dfrac{IJ}{AB}=\dfrac{IK}{AC}$
Donc, $\dfrac{IJ}{IK}=\dfrac{AB}{AC}$
De même on a : $\sin\widehat{A'B'J}=\dfrac{IJ}{A'B'}\;,\ \sin\widehat{A'C'K}=\dfrac{IK}{A'C'}$ et $\widehat{A'B'J}=\widehat{A'C'K}$
Alors, $\dfrac{IJ}{A'B'}=\dfrac{IK}{A'C'}$
Donc, $\dfrac{IJ}{IK}=\dfrac{A'B'}{A'C'}$
D'où, $$\boxed{\dfrac{AB}{AC}=\dfrac{A'B'}{A'C'}}$$
Démontrons que $\dfrac{AB}{BC}=\dfrac{A'B'}{B'C'}$
On a : $\sin\widehat{ABJ}=\dfrac{IJ}{AB}\;,\ \sin\widehat{BCK}=\dfrac{IK}{BC}$ et $\widehat{ABJ}=\widehat{BCK}$
Alors, $\dfrac{IJ}{AB}=\dfrac{IK}{BC}$
Donc, $\dfrac{IJ}{IK}=\dfrac{AB}{BC}$
De même on a : $\sin\widehat{A'B'J}=\dfrac{IJ}{A'B'}\;,\ \sin\widehat{B'C'K}=\dfrac{IK}{B'C'}$ et $\widehat{A'B'J}=\widehat{B'C'K}$
Alors, $\dfrac{IJ}{A'B'}=\dfrac{IK}{B'C'}$
Donc, $\dfrac{IJ}{IK}=\dfrac{A'B'}{B'C'}$
D'où, $$\boxed{\dfrac{AB}{BC}=\dfrac{A'B'}{B'C'}}$$
Démontrons que $\dfrac{BC}{AC}=\dfrac{B'C'}{A'C'}$
On a : $\sin\widehat{BCK}=\dfrac{JK}{BC}\;,\ \sin\widehat{ACK}=\dfrac{IK}{AC}$ et $\widehat{BCK}=\widehat{ACK}$
Alors, $\dfrac{JK}{BC}=\dfrac{IK}{AC}$
Donc, $\dfrac{JK}{IK}=\dfrac{BC}{AC}$
De même on a : $\sin\widehat{B'C'K}=\dfrac{IJ}{B'C'}\;,\ \sin\widehat{A'C'K}=\dfrac{IK}{A'C'}$ et $\widehat{B'C'K}=\widehat{A'C'K}$
Alors, $\dfrac{IJ}{B'C'}=\dfrac{IK}{A'C'}$
Donc, $\dfrac{IJ}{IK}=\dfrac{B'C'}{A'C'}$
D'où, $$\boxed{\dfrac{BC}{AC}=\dfrac{B'C'}{A'C'}}$$
II. Théorème de Thalès
II.1 Énoncé du théorème
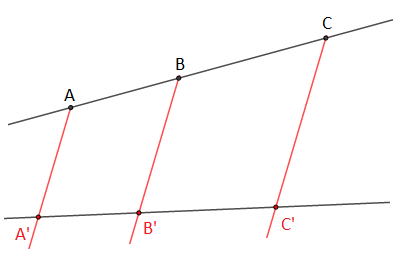
Si on coupe deux droites sécantes par trois droites parallèles alors on obtient sur les deux droites sécantes des segments de longueurs correspondants proportionnelles.
Traduction mathématique :
$$\text{Si }\left\lbrace\begin{array}{lll} A\;,\ B\;\text{ et } C\;\ \text{ alignés }\qquad\qquad\ \dfrac{AB}{AC}=\dfrac{A'B'}{A'C'}\quad (1)\\ \\ A'\;,\ B'\;\text{ et } C'\;\ \text{ alignés },\text{ alors }\;\;\dfrac{AB}{BC}=\dfrac{A'B'}{B'C'}\quad (2)\\ \\ (AA')\parallel(BB')\parallel(CC')\qquad\qquad\dfrac{BC}{AC}=\dfrac{B'C'}{A'C'}\quad (3)\end{array}\right.$$
II.2 Application du théorème de Thalès aux triangles
II.2.1 Activité
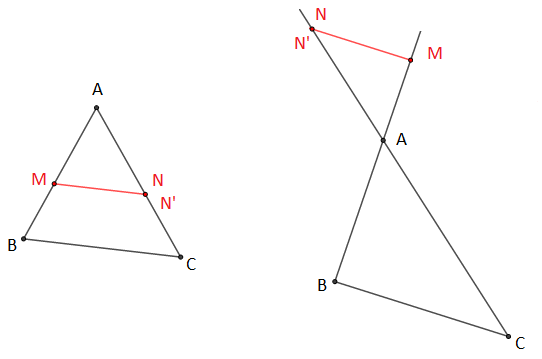
Soient $AMN$ et $ABC$ deux triangles obtenus en coupant deux droites sécantes en $A$ par deux droites parallèles $(MN)$ et $(BC).$
Soit $N'$ le projeté de $N$ sur la droite $(BC)$ parallèlement à la droite $(AB).$
Démontrons que $\dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{MN}{BC}$
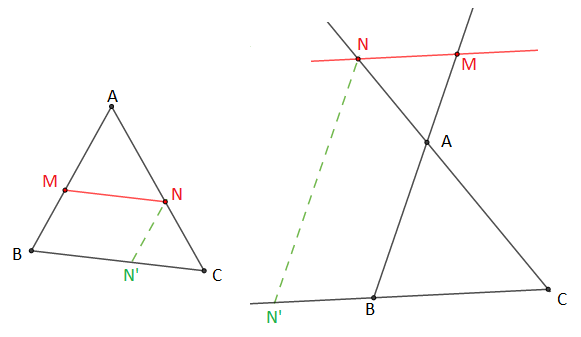
On a : les droites sécantes $(AB)$ et $(AC)$ coupées par les parallèles $(MN)$ et $(BC)$, alors $AMN$ et $ABC$ sont deux triangles en position de Thalès.
D'après le théorème de Thalès on aura : $\dfrac{AM}{AB}=\dfrac{AN}{AC}$
De même on a : les droites sécantes $(CA)$ et $(CB)$ coupées par les parallèles $(NN')$ et $(AB)$, alors $CNN'$ et $CAB$ sont deux triangles en situation de Thalès.
D'après le théorème de Thalès on aura : $\dfrac{AN}{AC}=\dfrac{BN'}{BC}$
Or, on a $BMNN'$ un parallélogramme, alors $MN=BN'$
Donc, $\dfrac{AN}{AC}=\dfrac{MN}{BC}$
D'où, $$\boxed{\dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{MN}{BC}}$$
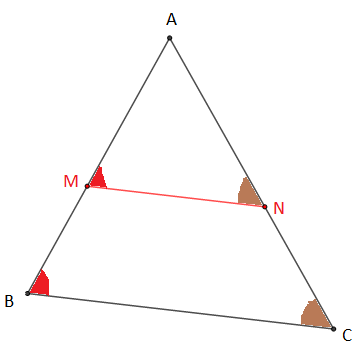
II.2.2 Énoncé du théorème
Si deux triangles sont en position de Thalès alors les longueurs des cotés correspondants sont proportionnelles.
$$\text{Si }\left\lbrace\begin{array}{lll}\left\lbrace\begin{array}{lll} M\in\;[AB] \\ N\in\;[AC] \end{array}\right.\quad\text{ou}\quad\left\lbrace\begin{array}{lll} A\in\;[BM] \\ A\in\;[CN]\end{array}\right.\quad\qquad\ \dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{MN}{BC}\quad\ (1)\\ \\ \qquad\qquad\qquad\qquad\quad\qquad\qquad\qquad\qquad\text{ alors }\;\;\dfrac{AM}{MB}=\dfrac{AN}{NC}\qquad\qquad (2)\\ \\ (MN)\parallel(BC)\qquad\qquad\qquad\qquad\qquad\qquad\qquad\dfrac{MB}{AB}=\dfrac{NC}{AC}\qquad\qquad (3)\end{array}\right.$$
II.2.3 Propriétés : agrandissement et réduction
Si deux triangles sont en position de Thalès alors l'un est un agrandissement (ou réduction) de l'autre.
Si le coefficient d'agrandissement (ou de réduction) est $k$ alors le coefficient d'agrandissement des aires est $k^{2}.$
On a $ABC$ un agrandissement de $AMN$.
Si $AB=k\times AM$ alors $\mathcal{A}(ABC)=k^{2}\mathcal{A}(AMN)$
III. Réciproque du théorème de Thalès
III.1 Activité
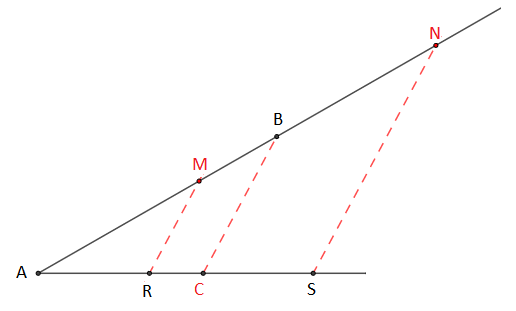
Soient $A\;,\ M$ et $B$ trois points alignés d'une part, $A\;,\ N$ et $C$ trois points alignés d'autre part, dans le même ordre tels que $\dfrac{AM}{AB}=\dfrac{AN}{AC}.$
Démontrons que $(MN)\parallel(BC)$
Soit $N'$ le projeté du point $M$ sur $[AC]$ parallèlement à $(BC).$
On aura $AMN$ et $ABC$ deux triangles en position de Thalès.
D'après le théorème de Thalès on aura $\dfrac{AM}{AB}=\dfrac{AN'}{AC}.$
Or, on a $\dfrac{AM}{AB}=\dfrac{AN}{AC}$, alors $AN'=AN$
Donc, $N=N'$
D'où, $(MN)\parallel(BC)$
III.2 Énoncé de la réciproque
Si $A\;,\ M$ et $B$ trois points alignés d'une part, $A\;,\ N$ et $C$ trois points alignés d'autre part, dans le même ordre tels que $\dfrac{AM}{AB}=\dfrac{AN}{AC}\;\left(\text{ ou }\;\dfrac{AM}{MB}=\dfrac{AN}{NC}\;\text{ ou }\;\dfrac{MB}{AB}=\dfrac{NC}{AC}\right)$ alors, les droites $(MN)$ et $(BC)$ sont parallèles.
IV. Application au construction
Soit $[AB]$ un segment de longueur $5\;cm$, $M$ un point de ce segment, $N$ un point de la demi-droite $[AB)$ tels que $AM=\dfrac{2}{3}AB$ et $AN=\dfrac{5}{3}AB.$
Plaçons les points $M$ et $N$
Auteur:
Abdoulaye Ba

Commentaires
Abdoulaye Ba (non vérifié)
sam, 09/29/2018 - 09:45
Permalien
Contribution
mndiaye
dim, 09/30/2018 - 00:03
Permalien
Je vous remercie de votre
Je vous remercie de votre commentaire. On va en prendre compte pour mieux améliorer. Pour les figures, on va regarder pour améliorer.
Sur quel support vous vous connectez au site? Smartphone ou ordinateur?
Sall (non vérifié)
lun, 11/05/2018 - 00:43
Permalien
Un grand merci pour le
Diatta (non vérifié)
sam, 01/30/2021 - 02:10
Permalien
Comment télécharger les cours
Diatta (non vérifié)
sam, 01/30/2021 - 02:14
Permalien
Sont bonnes
Diatta (non vérifié)
sam, 01/30/2021 - 02:12
Permalien
Télécharger gratuitement
Anonyme (non vérifié)
ven, 11/24/2023 - 20:35
Permalien
je n'ai pas très bien compris
Fatima solly (non vérifié)
ven, 07/19/2024 - 23:23
Permalien
Extraordinaire
Ajouter un commentaire