Solution des exercices : Inéquation et système d'inéquations du premier degré à une inconnue - 4e
Classe:
Quatrième
Exercice 1
Dans chacun des cas suivants, représentons graphiquement puis écrivons l'ensemble des solutions des inéquations suivantes.
Pour cet exercice, les parties hachurées constituent l'ensemble des solutions.
a) $x>-2$
Donc, on doit représenter sur un axe l'ensemble des nombres strictement supérieurs à $-2.$
Ainsi, $-2$ ne fera pas partie de la solution.
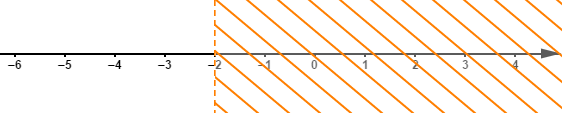
$$S=\left]-2\;;\ +\infty\right[$$
b) $x<+3$
On doit alors représenter sur un axe l'ensemble des nombres strictement inférieurs à $+3.$
Donc, $+3$ ne fera pas partie de la solution.

$$S=\left]-\infty\;;\ +3\right[$$
c) $x\geq -4$
Pour cela, on va représenter sur un axe l'ensemble des nombres supérieurs ou égaux à $-4.$
Ce qui signifie que, $-4$ fera partie de la solution.

$$S=\left[-4\;;\ +\infty\right[$$
d) $x>0$
On doit alors représenter sur un axe l'ensemble des nombres strictement positifs.

$$S=\left]0\;;\ +\infty\right[$$
e) $x\leq 6$
Pour cela, On représente sur un axe l'ensemble des nombres inférieurs ou égaux à $6$
Donc, $6$ fera partie de la solution.

$$S=\left]-\infty\;;\ 6\right]$$
f) $x\geq 0$
C'est l'ensemble des nombres positifs ou nuls.

$$S=\left[0\;;\ +\infty\right[$$
g) $x\leq -\dfrac{2}{3}$
On doit alors représenter sur un axe l'ensemble des nombres inférieurs ou égaux à $-\dfrac{2}{3}$
Ce qui signifie que $-\dfrac{2}{3}$ fera partie de la solution.

$$S=\left]-\infty\;;\ -\dfrac{2}{3}\right]$$
k) $x<-\dfrac{5}{3}$
C'est l'ensemble des nombres strictement inférieurs à $-\dfrac{5}{3}.$
Ainsi, $-\dfrac{5}{3}$ ne fait pas partie de la solution.

$$S=\left]-\infty\;;\ -\dfrac{5}{3}\right[$$
l) $x>\dfrac{17}{3}$
On représente alors, sur un axe l'ensemble des nombres strictement supérieurs à $\dfrac{17}{3}$
Ce qui signifie que $\dfrac{17}{3}$ ne fera pas partie de la solution.

$$S=\left]\dfrac{17}{3}\;;\ +\infty\right[$$
m) $x\geq -\dfrac{4}{5}$
C'est la représentation de l'ensemble des nombres supérieurs ou égaux à $-\dfrac{4}{5}.$
Donc, $-\dfrac{4}{5}$ fait partie de la solution.

$$S=\left[-\dfrac{4}{5}\;;\ +\infty\right[$$
o) $x\geq\dfrac{19}{7}$
On doit alors représenter sur un axe l'ensemble des nombres inférieurs ou égaux à $\dfrac{19}{7}$
Ce qui signifie que $\dfrac{19}{7}$ fera partie de la solution.

$$S=\left[\dfrac{19}{7}\;;\ +\infty\right[$$
p) $x>-\dfrac{103}{6}$
Pour cela, on représente sur un axe l'ensemble des nombres strictement supérieurs à $-\dfrac{103}{6}$
Ainsi, $-\dfrac{103}{6}$ ne fera pas partie de la solution.

$$S=\left]-\dfrac{103}{6}\;;\ +\infty\right[$$
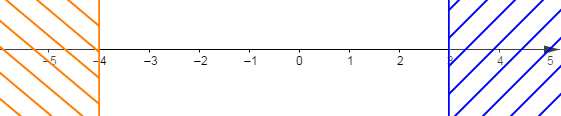



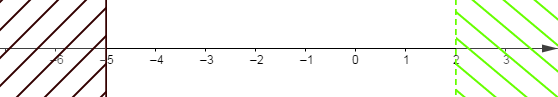


Exercice 5
On considère les deux cercles $\zeta_{1}(A\;;\ 2.3\;cm)\ $ et $\ \zeta_{2}(B\;;\ 5.4\;cm)$ tel que $AB=x+2.$
1) Donner toutes les valeurs entières possibles de $x$ pour que les cercles $\zeta_{1}$ et $\zeta_{2}$ soient sécants.
Les deux cercles sont sécants si, et seulement si, $|5.4-2.3|<AB<5.4+2.3$
En remplaçant $AB$ par $x+2$, on obtient :
$\zeta_{1}\ $ et $\ \zeta_{2}$ sont sécants si, et seulement si, $|3.1|<x+2<7.7$
Ce qui peut encore s'écrire :
$3.1<x+2\ $ et $\ x+2<7.7$
En résolvant ces inéquations, on obtient :
$3.1-2<x\ $ et $\ x<7.7-2$
Ce qui donne, $x>1.1\ $ et $\ x<5.7$
Donc, pour que les cercles $\zeta_{1}\ $ et $\ \zeta_{2}$ soient sécants, il faut que $x$ prenne des valeurs supérieures à $1.1$ et inférieures à $5.7$
Or, les valeurs entières supérieures à $1.1$ et inférieures à $5.7$ sont : $2\;;\ 3\;;\ 4\ $ et $\ 5$
Par conséquent, les valeurs entières possibles de $x$ pour que les cercles $\zeta_{1}\ $ et $\ \zeta_{2}$ soient sécants sont données par :
$$2\;;\ 3\;;\ 4\;;\ 5$$
2) Donnons la valeur de $x$ pour que les cercles $\zeta_{1}\ $ et $\ \zeta_{2}$ soient tangents extérieurement.
Les cercles $\zeta_{1}\ $ et $\ \zeta_{2}$ sont tangents extérieurement si, et seulement si, $AB=2.3+5.4$
C'est à dire ; $x+2=7.7$
En résolvant cette équation, on obtient :
$\begin{array}{rcrcl} x+2=7.7&\Leftrightarrow&x&=&7.7-2\\\\&\Leftrightarrow&x&=&5.7\end{array}$
Ainsi, les cercles $\zeta_{1}\ $ et $\ \zeta_{2}$ soient tangents extérieurement si $x=5.7$
3) Donnons toutes les valeurs de $x$ pour que les cercles $\zeta_{1}\ $ et $\ \zeta_{2}$ soient disjoints.
En effet, les cercles $\zeta_{1}\ $ et $\ \zeta_{2}$ soient disjoints signifie qu'ils sont soit disjoints extérieurement, soit disjoints intérieurement.
$-\ $ Les cercles $\zeta_{1}\ $ et $\ \zeta_{2}$ sont disjoints extérieurement si, et seulement si, $AB>2.3+5.4$
Donc, en remplaçant $AB$ par $x+2$, on obtient : $x+2>7.7$
Résolvons l'inéquation obtenue :
$\begin{array}{rcrcl} x+2>7.7&\Leftrightarrow&x&>&7.7-2\\\\&\Leftrightarrow&x&>&5.7\end{array}$
Donc, les valeurs de $x$ pour lesquelles $\zeta_{1}\ $ et $\ \zeta_{2}$ soient disjoints extérieurement sont données par :
$$S_{1}=]5.7\;;\ +\infty[$$
$-\ $ Les cercles $\zeta_{1}\ $ et $\ \zeta_{2}$ sont disjoints intérieurement si, et seulement si, $AB<|5.4-2.3|$
Ce qui donne : $x+2<3.1$
Résolvons cette inéquation :
$\begin{array}{rcrcl} x+2<3.1&\Leftrightarrow&x&<&3.1-2\\\\&\Leftrightarrow&x&<&1.1\end{array}$
Donc, les valeurs de $x$ pour lesquelles $\zeta_{1}\ $ et $\ \zeta_{2}$ soient disjoints intérieurement sont données par :
$$S_{2}=[0\;;\ 1.1[$$
Par suite, l'ensemble des valeurs de $x$ pour lesquelles $\zeta_{1}\ $ et $\ \zeta_{2}$ soient disjoints sont donné par :
$$S=S_{2}\cup S_{1}=[0\;;\ 1.1[\cup]5.7\;;\ +\infty[$$
Exercice 6
Dans chacun des cas suivants, représentons graphiquement puis écrivons l'ensemble des solutions des systèmes d'équations suivants.
Dans cet exercice, les parties non hachurées sont représentent les solutions du système.
1) $\left\lbrace\begin{array}{rcl} x&\geq&-4\\ x&\leq&3\end{array}\right.$
Sur une même droite graduée on représente les solutions de chaque inéquation.
On obtient alors :
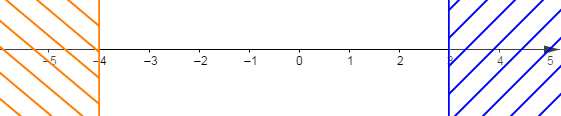
$$S=[-4\;;\ 3]$$
En effet, soit $S_{1}$ l'ensemble des solutions de la première inéquation et $S_{2}$ celui de la deuxième inéquation.
On a alors : $S_{1}=[-4\;;\ +\infty[\ $ et $\ S_{2}=]-\infty\;;\ 3]$
Par suite, l'ensemble des solutions du système est donné par :
$$S=S_{1}\cap S_{2}=[-4\;;\ 3]$$
2) $\left\lbrace\begin{array}{rcl} x&<&2\\ x&\geq&3 \end{array}\right.$
En représentant graphiquement les solutions de chaque inéquation sur une même droite graduée, on obtient :

$$S=\emptyset$$
On remarque qu'il n'existe pas de parties non hachurée.
Par conséquent, l'ensemble des solutions de ce système est l'ensemble vide ; noté :
$$S=\emptyset$$
3) $\left\lbrace\begin{array}{rcl} x&\leq&-4\\ x&\leq&-3 \end{array}\right.$
Représentons graphiquement les solutions de chaque inéquation du système sur une même droite graduée.
On obtient alors :

$$S=]-\infty\;;\ -4]$$
En effet, soit $S_{1}$ l'ensemble des solutions de la première inéquation et $S_{2}$ celui de la deuxième inéquation.
On a alors : $S_{1}=]-\infty\;;\ -4]\ $ et $\ S_{2}=]-\infty\;;\ -3]$
Par conséquent, l'ensemble des solutions du système est donné par :
$$S=S_{1}\cap S_{2}=]-\infty\;;\ -4]$$
4) $\left\lbrace\begin{array}{rcl} x&<&-1\\ x&\geq&4 \end{array}\right.$
On représente sur une même droite graduée les solutions de chaque inéquation.
On obtient alors :

$$S=\emptyset$$
On constate que toutes les parties sont hachurées. Ce qui signifie qu'il n'y a pas de solutions pour ce système.
D'où, $$S=\emptyset$$
5) $\left\lbrace\begin{array}{rcl} x&<&2\\ x&\geq&-5 \end{array}\right.$
En représentant graphiquement les solutions des deux inéquations du système sur une même droite graduée, on obtient :
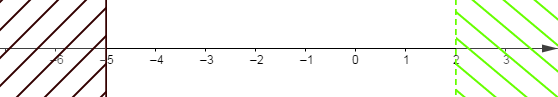
$$S=[-5\;;\ 2[$$
En effet, soit $S_{1}$ l'ensemble des solutions de la première inéquation et $S_{2}$ celui de la deuxième inéquation.
On a alors : $S_{1}=]--\infty\;;\ 2[\ $ et $\ S_{2}=[-5\;;\ +\infty[$
Ainsi, l'ensemble des solutions du système est donné par :
$$S=S_{1}\cap S_{2}=[-5\;;\ 2[$$
6) $\left\lbrace\begin{array}{rcl} x&\geq&-\dfrac{2}{3}\\ \\ x&\leq&\dfrac{2}{5} \end{array}\right.$
En représentant graphiquement les solutions des deux inéquations du système sur une même droite graduée, on obtient :

$$S=\left]-\dfrac{2}{3}\;;\ \dfrac{2}{5}\right]$$
En effet, soit $S_{1}$ l'ensemble des solutions de la première inéquation et $S_{2}$ celui de la deuxième inéquation.
On a alors : $S_{1}=\left[-\dfrac{2}{3}\;;\ +\infty\right[\ $ et $\ S_{2}=\left]-\infty\;;\ \dfrac{2}{5}\right]$
Par conséquent, l'ensemble des solutions du système est donné par :
$$S=S_{1}\cap S_{2}=\left]-\dfrac{2}{3}\;;\ \dfrac{2}{5}\right]$$
7) $\left\lbrace\begin{array}{rcl} x&>&-\dfrac{1}{2}\\ \\ x&\leq&+4 \end{array}\right.$
La représentation graphique des deux inéquations du système sur une même droite graduée donne :

$$S=\left]-\dfrac{1}{2}\;;\ 4\right]$$
En effet, soit $S_{1}$ l'ensemble des solutions de la première inéquation et $S_{2}$ celui de la deuxième inéquation.
On a alors : $S_{1}=\left]-\dfrac{1}{2}\;;\ +\infty\right[\ $ et $\ S_{2}=\left]-\infty\;;\ 4\right]$
D'où, l'ensemble des solutions du système est donné par :
$$S=S_{1}\cap S_{2}=\left]-\dfrac{1}{2}\;;\ 4\right]$$
Auteur:
Diny Faye

Commentaires
baye maguette diaw (non vérifié)
mer, 03/22/2023 - 14:26
Permalien
c'est bon
Anonyme (non vérifié)
sam, 05/18/2024 - 14:19
Permalien
Oui
Dorreus Medjina (non vérifié)
mer, 12/13/2023 - 22:00
Permalien
Bonsoir, ou est la correction
Anonyme (non vérifié)
dim, 04/13/2025 - 19:20
Permalien
c'est aussi ma question
Anonyme (non vérifié)
lun, 03/04/2024 - 21:04
Permalien
La solution des exercices n
Modou (non vérifié)
jeu, 04/25/2024 - 18:54
Permalien
MATHS
MARIAMA SARR (non vérifié)
jeu, 05/30/2024 - 20:45
Permalien
ORDINATEUR
Seynabou (non vérifié)
mar, 06/17/2025 - 22:49
Permalien
Où est la question de l
Ajouter un commentaire