Vous êtes ici

Corrigé devoir n° 2 maths - 3e

Classe:

Troisième

Exercice 1

On donne :

$A=3-\sqrt{2}\;,\quad B=\dfrac{5\sqrt{2}-1}{\sqrt{2}+1}\$ et

$\ C=\dfrac{1}{11-6\sqrt{2}}$

1) Montrons que

$B\$ et

$\ C$ sont des inverses.

On sait que :

$B\$ et

$\ C$ sont des inverses si, et seulement si,

$B\times C=1.$

Donc, calculons le produit

$B\times C$

Soit alors :

$\begin{array}{rcl} B\times C&=&\left(\dfrac{5\sqrt{2}-1}{\sqrt{2}+1}\right)\times\left(\dfrac{1}{11-6\sqrt{2}}\right)\\\\&=&\dfrac{5\sqrt{2}-1}{(\sqrt{2}+1)(11-6\sqrt{2})}\\\\&=&\dfrac{5\sqrt{2}-1}{11\sqrt{2}-12+11-6\sqrt{2}}\\\\&=&\dfrac{5\sqrt{2}-1}{5\sqrt{2}-1}\\\\&=&1\end{array}$

D'où,

$B\times C=1.$ Ce qui montre que

$B\$ et

$\ C$ sont des inverses.

2) Calculons

$A^{2}$ puis donnons une écriture simplifiée de

$\sqrt{C}$

Soit :

$A=3-\sqrt{2}$

Alors,

$\begin{array}{rcl} A^{2}&=&(3-\sqrt{2})^{2}\\\\&=&9-6\sqrt{2}+2\\\\&=&11-6\sqrt{2}\end{array}$

D'où,

$\boxed{A^{2}=11-6\sqrt{2}}$

Donnons une écriture simplifiée de

$\sqrt{C}$

Soit :

$C=\dfrac{1}{11-6\sqrt{2}}$

Or,

$11-6\sqrt{2}=A^{2}$

Donc, en remplaçant

$11-6\sqrt{2}$ par

$A^{2}$ , on obtient :

$C=\dfrac{1}{A^{2}}$

Par suite,

$\begin{array}{rcl} \sqrt{C}&=&\sqrt{\dfrac{1}{A^{2}}}\\\\&=&\dfrac{\sqrt{1}}{\sqrt{A^{2}}}\\\\&=&\dfrac{1}{|A|}\\\\&=&\dfrac{1}{|3-\sqrt{2}|}\end{array}$

Donc,

$\sqrt{C}=\dfrac{1}{|3-\sqrt{2}|}$ , mais on sait que

$(3-\sqrt{2})>0.$

Déterminons alors le signe de

$(3-\sqrt{2}).$

On a :

$3\$ et

$\ \sqrt{2}$ sont tous positifs et

$3^{2}=9$ est supérieur à

$(\sqrt{2})^{2}=2.$ Par conséquent,

$3$ est supérieur à

$\sqrt{2}.$ Par suite,

$(3-\sqrt{2})>0.$

Ainsi,

$\sqrt{C}=\dfrac{1}{|3-\sqrt{2}|}=\dfrac{1}{3-\sqrt{2}}$

Donc, en rendant rationnel le dénominateur, on obtient :

$\begin{array}{rcl} \sqrt{C}&=&\dfrac{1}{3-\sqrt{2}}\\\\&=&\dfrac{3+\sqrt{2}}{(3-\sqrt{2})(3+\sqrt{2})}\\\\&=&\dfrac{3+\sqrt{2}}{3^{2}-(\sqrt{2})^{2}}\\\\&=&\dfrac{3+\sqrt{2}}{9-2}\\\\&=&\dfrac{3+\sqrt{2}}{7}\end{array}$

D'où,

$\boxed{\sqrt{C}=\dfrac{3+\sqrt{2}}{7}}$

3) Donnons un encadrement de

$\sqrt{C}$ à

$10^{-2}$ près.

Comme

$1.414<\sqrt{2}<1.415$ alors, on a :

$\begin{array}{rcccl} 3+1.414&<&3+\sqrt{2}&<&3+1.415\\\\4.414&<&3+\sqrt{2}&<&4.415\\\\\dfrac{4.414}{7}&<&\dfrac{3+\sqrt{2}}{7}&<&\dfrac{4.415}{7}\\\\0.6305&<&\dfrac{3+\sqrt{2}}{7}&<&0.6307\\\\0.6305&<&\sqrt{C}&<&0.6307\end{array}$

Ainsi, un encadrement de

$\sqrt{C}$ à

$10^{-2}$ près sera donné par :

$0.63<\sqrt{C}<0.64$

Exercice 2

Soit

$X=\dfrac{\dfrac{3\sqrt{2}}{2}-2}{\sqrt{3}-2}-\left(4-3\sqrt{\dfrac{3}{2}}\right)\$ et

$\ Y=30-12\sqrt{6}$

1) Montrons que

$X$ peut s'écrire sous la forme

$a\sqrt{2}+b\sqrt{3}$ où

$a\$ et

$\ b$ sont des entiers relatifs.

On a :

$\begin{array}{rcl} X&=&\dfrac{\dfrac{3\sqrt{2}}{2}-2}{\sqrt{3}-2}-\left(4-3\sqrt{\dfrac{3}{2}}\right)\\\\&=&\dfrac{\dfrac{3\sqrt{2}-4}{2}}{\sqrt{3}-2}-4+3\dfrac{\sqrt{3}}{\sqrt{2}}\\\\&=&\dfrac{3\sqrt{2}-4}{2(\sqrt{3}-2)}-4+3\dfrac{\sqrt{3}\times\sqrt{2}}{2}\\\\&=&\dfrac{(3\sqrt{2}-4)(\sqrt{3}+2)}{2(\sqrt{3}-2)(\sqrt{3}+2)}-4+\dfrac{3\sqrt{6}}{2}\\\\&=&\dfrac{3\sqrt{6}+6\sqrt{2}-4\sqrt{3}-8}{2(3-4)}-4+\dfrac{3\sqrt{6}}{2}\\\\&=&\dfrac{3\sqrt{6}+6\sqrt{2}-4\sqrt{3}-8}{-2}-4+\dfrac{3\sqrt{6}}{2}\\\\&=&\dfrac{-3\sqrt{6}-6\sqrt{2}+4\sqrt{3}+8}{2}-4+\dfrac{3\sqrt{6}}{2}\\\\&=&-\dfrac{3\sqrt{6}}{2}-\dfrac{6\sqrt{2}}{2}+\dfrac{4\sqrt{3}}{2}+4-4+\dfrac{3\sqrt{6}}{2}\\\\&=&-3\sqrt{2}+2\sqrt{3}\end{array}$

Donc,

$\boxed{X=2\sqrt{3}-3\sqrt{2}}$

2) Déduisons une écriture plus simplifiée de

$X^{2}$

On a :

$X=2\sqrt{3}-3\sqrt{2}$

Alors,

$\begin{array}{rcl} X^{2}&=&(2\sqrt{3}-3\sqrt{2})^{2}\\\\&=&(2\sqrt{3})^{2}-12\sqrt{6}+(-3\sqrt{2})^{2}\\\\&=&12-12\sqrt{6}+18\\\\&=&30-12\sqrt{6}\end{array}$

Ainsi,

$\boxed{X^{2}=30-12\sqrt{6}}$

3) Calculons

$\sqrt{Y}$

Soit :

$Y=30-12\sqrt{6}$

Alors, on constate que

$Y=X^{2}$

Donc,

$\sqrt{Y}=\sqrt{X^{2}}=|X|$

Déterminons alors le signe de

$X$

On a :

$(2\sqrt{3})\$ et

$\ (3\sqrt{2})$ sont tous positifs.

Alors,

$(2\sqrt{3})^{2}=12\$ et

$\ (3\sqrt{2})^{2}=18$

$12<18$ donc,

$(2\sqrt{3})$ est inférieur à

$(3\sqrt{2})$

Par suite,

$X<0$

Ainsi,

$\sqrt{Y}=|X|=-X$

D'où,

$\boxed{\sqrt{Y}=-2\sqrt{3}+3\sqrt{2}}$

4) On pose :

$Z=\dfrac{X}{Y}$

Donnons une écriture simplifiée puis un encadrement de

$Z$ à

$10^{-3}$ près, sachant que

$1.414<\sqrt{2}<1.415\$ et

$\ 1.732<\sqrt{3}<1.733$

On a :

$Z=\dfrac{X}{Y}=\dfrac{2\sqrt{3}-3\sqrt{2}}{30-12\sqrt{6}}$

On sait que :

$Y=30-12\sqrt{6}=X^{2}$

Donc, en remplaçant, on obtient :

$\begin{array}{rcl} Z&=&\dfrac{X}{X^{2}}\\\\&=&\dfrac{X}{X\times X}\\\\&=&\dfrac{1}{X}\\\\&=&\dfrac{1}{2\sqrt{3}-3\sqrt{2}}\\\\&=&\dfrac{2\sqrt{3}+3\sqrt{2}}{(2\sqrt{3}-3\sqrt{2})(2\sqrt{3}+3\sqrt{2})}\\\\&=&\dfrac{2\sqrt{3}-3\sqrt{2}}{12-18}\\\\&=&\dfrac{2\sqrt{3}-3\sqrt{2}}{-6}\\\\&=&\dfrac{3\sqrt{2}-2\sqrt{3}}{6}\end{array}$

D'où,

$\boxed{Z=\dfrac{3\sqrt{2}-2\sqrt{3}}{6}}$

Donnons un encadrement de

$Z$ à

$10^{-3}$ près.

Comme

$1.732<\sqrt{3}<1.733$ alors, en multipliant par

$2$ on a :

$2\times 1.732<2\times\sqrt{3}<2\times 1.733\ \Rightarrow\ 3.464<2\sqrt{3}<3.466$

En multipliant cette dernière relation par

$-1$ , les inégalités changent de sens.

Ainsi :

$-3.466<-2\sqrt{3}<-3.464\quad(1)$

Par ailleurs, comme

$1.414<\sqrt{2}<1.415$ alors, en multipliant par

$3$ on obtient :

$3\times 1.414<3\times\sqrt{2}<3\times 1.415$

Ce qui donne :

$4.242<3\sqrt{2}<4.245\quad(2)$

En additionnant membre à membre les inégalités

$(1)\$ et

$\ (2)$ , on obtient :

$4.242-3.466<3\sqrt{2}-2\sqrt{3}<4.245-3.464\ \Rightarrow\ 0.776<3\sqrt{2}-2\sqrt{3}<0.781$

En divisant par

$6$ , on trouve :

$\dfrac{0.776}{6}<\dfrac{3\sqrt{2}-2\sqrt{3}}{6}<\dfrac{0.781}{6}\ \Rightarrow\ 0.129<\dfrac{3\sqrt{2}-2\sqrt{3}}{6}<0.130$

Donc, un encadrement de

$Z$ à

$10^{-3}$ près sera donné par :

$0.129<Z<0.130$

Exercice 3

Soit

$A=\sqrt{\left(x-\dfrac{3}{2}\right)^{2}}-\dfrac{1}{2}$

1) Donnons une écriture plus simplifiée de

$A$

On a :

$\begin{array}{rcl} A&=&\sqrt{\left(x-\dfrac{3}{2}\right)^{2}}-\dfrac{1}{2}\\\\&=&\left|x-\dfrac{3}{2}\right|-\dfrac{1}{2}\end{array}$

Alors,

$\boxed{A=\left|x-\dfrac{3}{2}\right|-\dfrac{1}{2}}$

2) Soit

$f$ une application affine définie dans

$\mathbb{R}$ par :

$f(x)=\left|x-\dfrac{3}{2}\right|-\dfrac{1}{2}$

Montrons que

$f$ est une application affine par intervalles

On a :

$x-\dfrac{3}{2}=0$ si, et seulement si,

$x=\dfrac{3}{2}$

Soit alors, le tableau de signe suivant :

$\begin{array}{|c|lclcr|}\hline x&-\infty&&\dfrac{3}{2}&&+\infty\\\hline\text{signe de : } x-\dfrac{3}{2}& &-&0&+&\\\hline f(x)&&-x+\dfrac{3}{2}-\dfrac{1}{2}&|&x-\dfrac{3}{2}-\dfrac{1}{2}&\\\hline\end{array}$

D'après le tableau ci-dessus, on a :

$-\$ si

$x\in\;\left]-\infty\;;\ \dfrac{3}{2}\right]\;,\ \ f(x)=-x+\dfrac{2}{2}=-x+1$

$-\$ si

$x\in\;\left[\dfrac{3}{2}\;;\ +\infty\right[\;,\ \ f(x)=x-\dfrac{4}{2}=x-2$

Ce qui montre que

$f$ est une application affine par intervalle.

3) Représentons graphiquement

$f(x)$ dans l'intervalle

$\left[-\dfrac{3}{2}\;;\ \dfrac{3}{2}\right]$

Lorsque

$x$ appartient à l'intervalle

$\left[-\dfrac{3}{2}\;;\ \dfrac{3}{2}\right]$ alors, on a :

$f(x)=-x+1$

Ainsi, représenter graphiquement

$f$ dans

$\left[-\dfrac{3}{2}\;;\ \dfrac{3}{2}\right]$ c'est représenter :

$(\Delta)\;:\ y=-x+1$ dans

$\left[-\dfrac{3}{2}\;;\ \dfrac{3}{2}\right]$

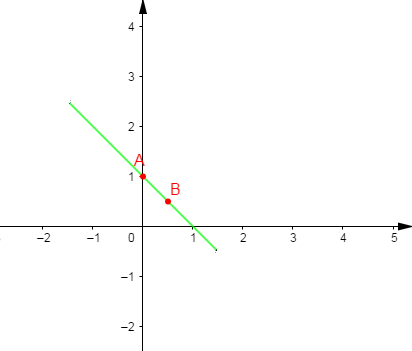
Soit alors deux points

$A\$ et

$\ B$ appartenant à

$(\Delta).$

On a :

$\begin{array}{|c|c|c|}\hline&A&B\\\hline x&0&\dfrac{1}{2}\\\hline y&1&\dfrac{1}{2}\\\hline\end{array}$

Plaçons alors les points

$A\$ et

$\ B$ dans un repère

$(O\;,\ \vec{i}\;,\ \vec{j})$ et traçons la droite

$(\Delta)$ passant par ces deux points et délimitée dans l'intervalle

$\left[-\dfrac{3}{2}\;;\ \dfrac{3}{2}\right].$

4) Déduisons la solution de l'équation

$\left|x-\dfrac{3}{2}\right|=\dfrac{1}{2}$ sur l'intervalle

$\left[-\dfrac{3}{2}\;;\ \dfrac{3}{2}\right].$

On a :

$\left|x-\dfrac{3}{2}\right|=\dfrac{1}{2}$ si, et seulement si,

$\left|x-\dfrac{3}{2}\right|-\dfrac{1}{2}=0$

C'est à dire ;

$f(x)=0$

Or, dans l'intervalle

$\left[-\dfrac{3}{2}\;;\ \dfrac{3}{2}\right]$ , on a :

$f(x)=-x+1$

Donc,

$\begin{array}{rcl} f(x)=0&\Leftrightarrow&-x+1=0\\\\&\Leftrightarrow&-x=-1\\\\&\Leftrightarrow&x=1\end{array}$

D'où,

$\boxed{S=\{1\}}$

Exercice 4

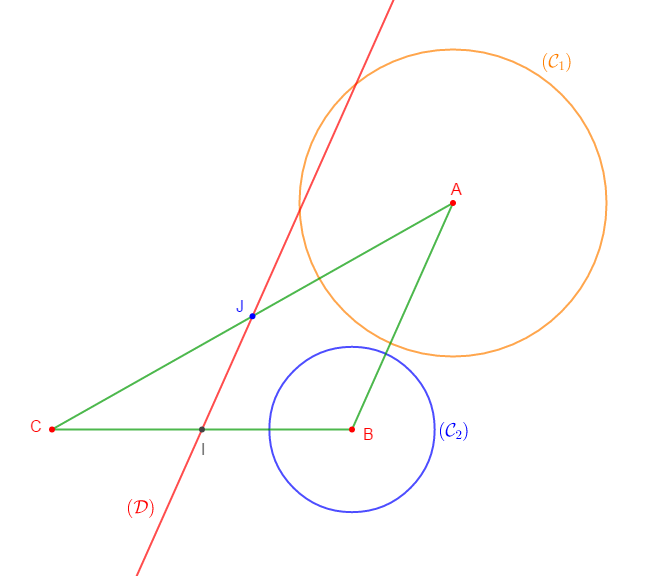
On considère un triangle

$ABC$ tel que :

$AB=c\;,\ AC=b\ \text{ et }\ BC=6\;cm$

1) Traçons deux cercle

$\mathcal{C}_{1}\left(A\;,\ \dfrac{b}{3}\right)\$ et

$\ \mathcal{C}_{2}\left(B\;,\ \dfrac{c}{3}\right)$

2) Soit

$I$ milieu de

$[BC]$ , la droite

$(\mathcal{D})$ passant par

$I$ et parallèle à

$(AB)$ coupe

$(AC)$ en

$J.$

Montrons que

$J$ est milieu de

$[AC]$

On a :

$ABC$ un triangle et la droite

$(\mathcal{D})$ passant par

$I$ milieu de

$[BC]$ parallèlement à

$(AB)$ coupe le troisième côté de ce triangle en

$J.$

Or, d'après le théorème de la droite des milieux, la droite

$(\mathcal{D})$ passe par le milieu de

$[AC].$

D'où,

$J$ est le milieu de

$[AC].$

Auteur:

Diny Faye

Commentaires

Amy thiam (non vérifié)

lun, 01/09/2023 - 07:44

Permalien

Étudie

Les cours sont très bien

répondre

BOLOL (non vérifié)

dim, 12/17/2023 - 16:13

Permalien

EXELLENT

répondre

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Corrigé devoir n° 2 maths - 3e

Formulaire de recherche

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Commentaires

Étudie

EXELLENT

Ajouter un commentaire

Plain text