Vous êtes ici

Série d'exercices sur la Cinétique chimique - Ts

Classe:

Terminale

Exercice 1

La réaction de décomposition de l'eau oxygénée $H_{2}O_{2}$ se fait suivant l'équation :

$$2H_{2}O_{2}\quad\rightarrow\quad O_{2}\ +\ 2H_{2}O$$

pour étudier la cinétique de cette réaction, on réalise l'expérience sur un volume $V=10\,cm^{3}$ de solution d'eau oxygénée de concentration molaire $C_{0}=6\cdot 10^{-2}mol^{-1}.$

(Durant l'expérience $V$ est constant et le volume molaire d'un gaz est $V_{M}=24\,L\cdot mol^{-1}.$

On note à divers instants $t$ le volume $V_{O_{2}}$ de dioxygène dégagé.

On établit le tableau suivant :

$$\begin{array}{|c|c|c|c|c|c|c|} \hline t(min)&0&5&10&15&20&30\\ \hline V_{O_{2}}\left(10^{-3}L\right)& &1.56& &3.65& &5.26\\ \hline C=\left[H_{2}O_{2}\right]\left(10^{-2}mol/L\right)&6& &3.7& &2.3&\\ \hline \end{array}$$

1) Montrer que la concentration molaire de l'eau oxygénée restante est donnée par :

$$\left[H_{2}O_{2}\right]=C=C_{0}-\dfrac{2V_{O_{2}}}{V\cdot V_{M}}$$

2) Reproduire et compléter le tableau.

3) Tracer la courbe $C=f(t).$

4) Définir la vitesse instantanée de disparition de $H_{2}O_{2}$ et déterminer sa valeur maximale.

5) Tracer sur le même graphique la courbe obtenue si l'expérience est réalisée à une température supérieur à celle de la première expérience.

Exercice 2

Des tubes à essais fermés contenant chacun $0.6\,g$ d'un alcool primaire $A$ de formule $C_{3}H_{7}OH$ et $0.6\,g$ d'acide éthanoique $CH_{3}COOH$ sont placés à la date $t=0$ dans l'eau bouillante.

1) Écrire l'équation de la réaction et donner le nom de l'ester formé.

2) A la date $t=2\,min$, on fait sortir un tube et on dose l'acide éthanoique restant par $V_{B}=21.7\,cm^{3}$ d'une solution de soude $\left(NaOH\right)$ de concentration molaire $C_{B}=0.4\,mol\cdot L^{-1}.$

a) Indiquer le mode opératoire du dosage.

b) Déterminer la composition du mélange à cette date

3) On répété les mêmes opérations et on obtient le tableau suivant :

$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline t(min)&0&5&10&15&20&40&60&80&100&120&150&180&200\\ \hline n_{ester}\left(10^{-3}mol\right)&0&2.5&3.7&4.5&4.9&5.7&6&6.4&6.5&6.6&6.7&6.7&6.7\\ \hline \end{array}$$

a) Tracer la courbe $n_{ester}=f(t)$ et interpréter ces différentes parties.

b) Déterminer la vitesse moyenne de formation de l'ester entre $t_{1}=10\,min\text{ et }t_{2}=50\,min$

c) Déterminer le rendement d'estérification

d) Déterminer la constante d'équilibre, relative à la réaction d'estérification.

e) Peut-on utiliser un catalyseur pour :

$-\ $ Augmenter la vitesse de la réaction

$-\ $ Augmenter le rendement de la réaction

Exercice 3

A $t=0\,s$, on introduit un volume $V_{1}=200\,mL$ d'une solution $(S_{1})$ d'iodure de potassium $KI$ de concentration molaire $C_{1}$, un volume $V_{2}=300\,mL$ d'une solution $(S_{2})$ de péroxodisulfate de potassium $K_{2}S_{2}O_{8}$ de concentration molaire $C_{2}=10^{-2}mol\cdot L^{-1}$ et quelques gouttes d'empois d'amidon.

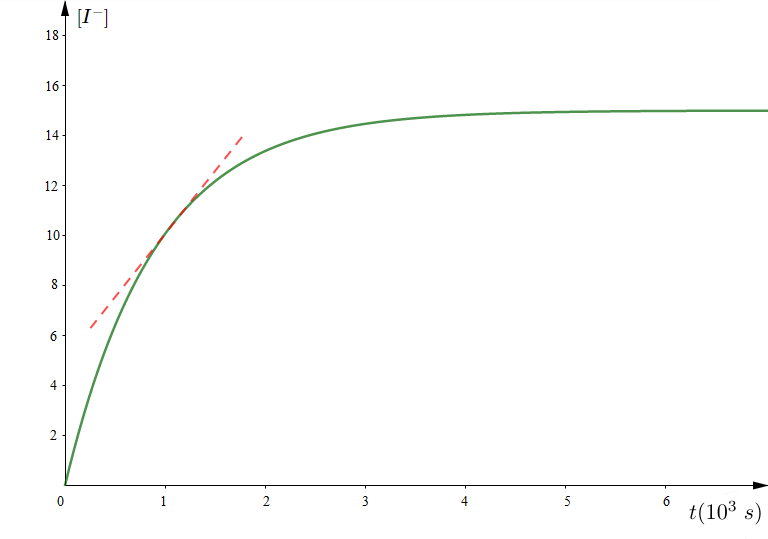
Une étude expérimentale a permis de tracer la courbe des variations de la concentration de l'ion iodure $I^{-}$ en fonction du temps (voir figure).

1) Écrire l'équation de la réaction chimique symbolisant la réaction d'oxydoréduction supposée lente et totale.

Préciser les couples rédox mis en jeu.

2) a) Définir la vitesse de la réaction à la date $t.$

b) Montrer que son expression s'écrit sous la forme $v=-\dfrac{V}{2}\dfrac{d\left[I^{-}\right]}{dt}.$

Avec $V$ volume du mélange réactionnel.

c) Comment varie cette vitesse au cours du temps ?

Justifier.

Déterminer sa valeur maximale

3) a) Définir la vitesse moyenne $v_{moy}$ de la réaction.

Donner son expression en fonction de $\dfrac{\Delta\left[I^{-}\right]}{\Delta t}$ ou $\Delta\left[I^{-}\right]$ est la variation de la concentration des ions $I^{-}$ pendant la durée $\Delta t.$

b) Calculer sa valeur entre les instants $t_{1}=0\text{ et }t_{2}=4\,min.$

4) a) Dresser le tableau descriptif d'évolution du système chimique.

b) En utilisant le graphe, déterminer la quantité de matière initiale $n_{0}\left(I^{-}\right)$ dans le mélange.

Déduire la valeur de $C_{1}.$

c) Définir le temps de demi - réaction $(t_{1/2}).$

Sachant que $t_{1/2}=4\,min$, déterminer l'avancement final (maximal) de la réaction.

d) Quel est le réactif limitant ?

e) Compléter la courbe de $[I^{-}]=f(t)$ sachant que la réaction se termine à la date $t_{1}=32\,min$ (voir figure).

Exercice 4

A température constante on étudie la cinématique de décomposition de l'eau oxygénée.

L'équation bilan est la suivante :

$$2H_{2}O_{2_{(Iq)}}\quad\rightarrow\quad 2H_{2}O_{(g)}\ +\ O_{2_{(g)}}$$

au début de l'expérience, la concentration en eau oxygénée est de $8\cdot10^{-2}mol\cdot L^{-1}.$

(L'expérience est réalisée avec $1\,L$ d'eau oxygénée et ce volume est considéré comme constant au cours de l'expérience).

On mesure le volume de dioxygène dégagé au cours du temps. (voir le tableau de mesure ci-dessous) le volume molaire des gaz à cette température est $V_{m}=24\,L\cdot mol^{-1}.$

1) exprimer la quantité de matière en dioxygène formée à l'instant $t$ (notée $n\left(O_{2}\right)t$) en fonction de $V\left(O_{2}\right)t$ et de $V_{m}.$

2) Dresser le tableau d'avancement pour cette réaction.

Calculer la valeur de l'avancement maximal.

3) Compléter le tableau de mesures suivant.

$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|} \hline t(min)&0&5&10&15&20&25&30&40&60\\ \hline V_{O_{2}}(L)&0&0.2&0.31&0.40&0.48&0.54&0.58&0.65&0.72\\ \hline x\left(10^{-2}mol\right)& & & & & & & & &\\ \hline \end{array}$$

4) Tracer la courbe $x=f(t).$

5) Calculer la vitesse moyenne de la réaction entre les instants $t_{1}=10\,min\text{ et }t_{2}=25\,min.$

6) Définir la vitesse instantanée $v$ de la réaction et la déterminer graphiquement à $t=20\,min.$

Comment évolue cette vitesse au cours du temps ?

7) Déterminer graphiquement le temps de demi réaction $t_{1/2}$ et déduire le taux d'avancement $\left(\tau=\dfrac{x\left(t_{1/2}\right)}{x_{max}}\right)$ à cette date.

Exercice 5

Pour étudier la cinétique de la réaction d'oxydation des ions iodures $I^{-}$ par les ions peroxodisulfate $S_{2}O_{8}^{2-}$, on réalise à $t_{0}=0\,s$ et à une température $T$ constante, un mélange de deux solutions $(S_{1})$ et $(S_{2}).$

$(S_{1})$ : solution d'iodure de potassium $KI$ de volume $V_{1}=30\,mL$ et de concentration $C_{1}.$

$(S_{2})$ : de peroxodisulfate de potassium $K_{2}S_{2}O_{8}$ de volume $V_{2}=30\,mL$ et de concentration $C_{2}=0.05 mol\cdot L^{-1}.$

La réaction produite dans le mélange est totale et lente d'équation :

$$2I^{-}\quad +\quad S_{2}O_{8}^{2-}\quad\rightarrow\quad I_{2}\quad +\quad 2SO_{4}^{2-}$$

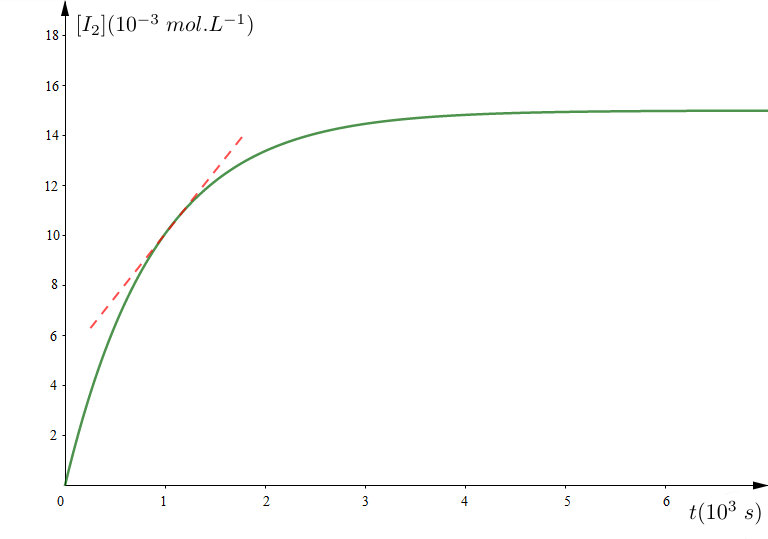
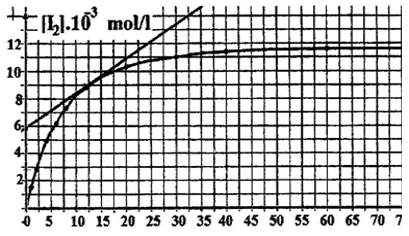
La courbe de la figure 1 donne la variation de la concentration molaire de diiode en fonction du temps.

1) a) Calculer la concentration initiale du mélange en ions peroxodisulfate : $\left[S_{2}O_{8}^{2-}\right]0.$

b) Dresser le tableau d'avancement et déduire que $I^{-}$ est le réactif limitant.

c) Déterminer la concentration initiale de $I^{-}$ dans le mélange : $[I^{-}]0.$

d) En déduire $C_{1}.$

2) Déterminer, en $mol\cdot L^{-1}$, la composition du mélange à l'instant $t_{1}=1000\,s.$

3) Déterminer la vitesse volumique moyenne de la réaction entre les dates $t_{0}=0\,s\text{ et }t_{1}=1000\,s.$

4) a) Définir la vitesse instantanée de la réaction.

b) Comment varie cette vitesse au cours du temps ?

Justifier à l'aide du graphique.

c) Déterminer la valeur de la vitesse volumique de la réaction à la date $t_{1}=1000\,s.$

5) La courbe $[I_{2}]=f(t)$ est obtenue en dosant à différentes dates des prélèvements du mélange par une solution $(S)$ de thiosulfate de sodium $Na_{2}S_{2}O_{3}$ de concentration molaire $C.$

a) Écrire l'équation de la réaction du dosage.

b) Calculer $C$ sachant que $5\,mL$ du mélange sont dosés à la date $t_{1}=1000\,s$ par $v=2\,mL$ de la solution $(S).$

Exercice 6

L'eau oxygénée $H_{2}O_{2}$ se décompose lentement à la température ambiante et en présence d'un catalyseur suivant l'équation :

$$2H_{2}O_{2(l)}\quad\rightarrow\quad 2H_{2}O_{(g)}\ +\ O_{2(g)}$$

Pour étudier la cinétique de cette réaction on prépare des prélèvements identiques de volume $V_{p}$ chacun et on dose la quantité de $H_{2}O_{2}$ restante par une solution de permanganate de potassium $KM_{n}O_{4}$ en milieu acide de concentration molaire $C=0.5\,mol\cdot L^{-1}.$

Soit $V$ : le volume de la solution de $KMnO_{4}$ nécessaire pour obtenir l'équivalence.

L'équation de la réaction de dosage s'écrit :

$$5H_{2}O_{2}\ +\ 2MnO_{4}^{-}\ +\ 6H^{+}\quad\rightarrow\quad 5O_{2}\ +\ 2Mn^{2+}\ +\ 8H_{2}O.$$

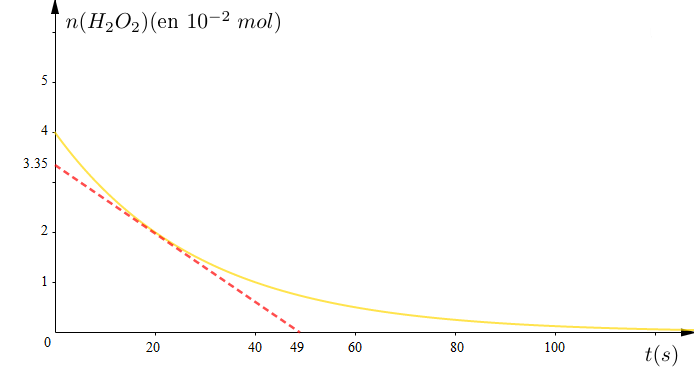
On donne la courbe $n\left(H_{2}O_{2}\right)=f(t).$

1) Dresser le tableau d'avancement de la réaction étudiée.

Quel est l'avancement maximal.

2) a) Définir la vitesse instantanée de la réaction étudiée.

b) Déterminer sa valeur à la date $t=20\,min.$

c) Comment évolue cette vitesse au cours du temps ?

Exprimer.

3) Définir la vitesse moyenne et la calculer entre $t_{1}=0\,min\text{ et }t_{2}=40\,min.$

4) a) Quel est le volume $V$ de la solution de $KMnO_{4}$ nécessaire pour le dosage à la date $t=20\,min.$

b) Déterminer la date à laquelle disparait $75\%$ de la quantité initiale de $H_{2}O_{2}.$

Quel est la valeur du taux d'avancement de la réaction à cette date.

Exercice 7

1) Les ions peroxodisulfate $S_{2}O_{8}^{2-}$ oxydent lentement les ions iodures $I^{-}.$

Établir l'équation bilan de cette réaction.

2) A la date $t=0$, et à une température constante, on mélange :

$-\ $ Un volume $V_{1}=50\,mL$ d'une solution aqueuse de peroxdisulfate d'ammonium $\left(NH_{4}\right)_{2}S_{2}O_{8}$ de concentration molaire $C_{1}=5\cdot 10^{-2}mol\cdot L^{-1}.$

$-\ $ Un volume $V_{2}=50\,mL$ d'une solution aqueuse d'iodure de potassium $KI$ de concentration molaire $C_{2}=16\cdot 10^{-2}mol\cdot L^{-1}.$

$-\ $ Quelques gouttes d'une solution d'empois d'amidon fraichement préparé (on rappelle que l'empois d'amidon colore en bleu nuit une solution contenant du diiode $I_{2}$ même en faible quantité).

A une date $t$, on prélève, du mélange réactionnel, un volume $V=10\,mL$ qu'on lui ajoute de l'eau glacée et on dose la quantité de diiode $I_{2}$ formée par une solution de thiosulfate de sodium $NaS_{2}O_{3}$ selon la réaction rapide et totale d'équation :

$$2S_{2}O_{3}^{2-}\ +\ I_{2}\quad\rightarrow\quad S_{4}O_{6}^{2-}\ +\ 2I^{-}$$

a) Décrire brièvement l'expérience de ce dosage, préciser comment peut - on reconnaitre expérimentalement le point d'équivalence ?

b) Calculer la concentration molaire initiale des ions iodure $[I^{-}]_{0}$ et des ions peroxodisulfate $[S_{2}O_{8}^{2-}]_{0}$ dans le mélange réactionnel.

c) Dresser le tableau d'avancement de la réaction qui se produit dans chaque prélèvement.

3) On définit l'avancement volumique y par le rapport de l'avancement $x$ par le volume $V$ du milieu réactionnel $y=\dfrac{x}{v}$ (les constituants du système chimique constituent la même phase et le volume du milieu réactionnel est constant).

Monter qu'on a à la date $t$ $[I^{-}]_{t}=[I^{-}]_{0}-2y.$

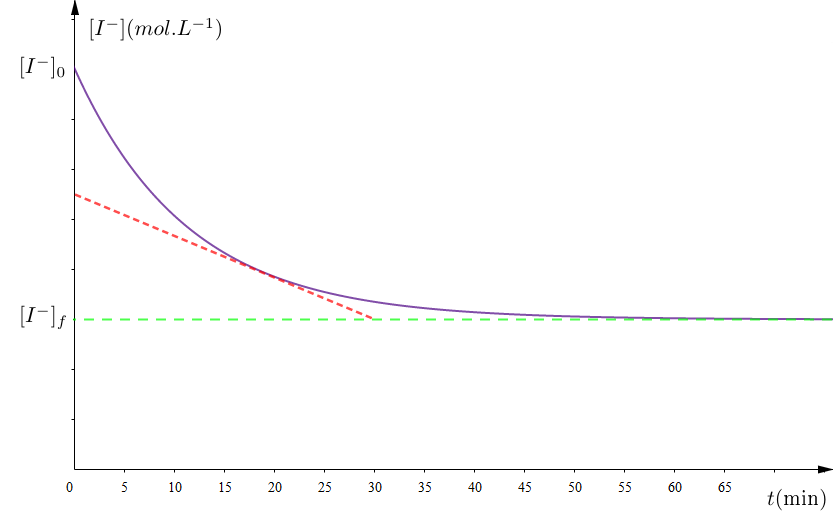
4) Les résultats des dosages ont permis de tracer la courbe régissant les variations de la concentration des ions iodure au cours du temps ( voir figure).

a) Préciser,en le justifiant,le réactif limitant.

b) En utilisant le tableau d'avancement, déterminer la concentration final en ions iodure $[I^{-}]_{f}.$

c) Définir la vitesse volumique d'une réaction chimique.

Montrer qu'elle s'écrit sous la forme $V_{vol}=-\dfrac{1\mathrm{d}[I^{-}]}{2\mathrm{d}t}.$

Déterminer graphiquement sa valeur à la date $t=20\,min.$

Déduire la vitesse instantanée à cette date.

5) On refait l'expérience précédente mais avec une solution d'iodure de potassium de volume $v_{2}=50\,mL$ et de concentration molaire $C'_{2}=18\cdot10^{-2}mol\cdot L^{-1}$, représenter, sur le même graphe de la figure 1, l'allure de la courbe représentant $[I^{-1}]=f(t).$

Exercice 7

Pour préparer l'éthanoate de butyle $CH_{3}COO-(CH_{2})_{3}-CH_{3}$, ester au parfum de banane, on réalise un mélange équimolaire d'acide éthanoique $CH_{3}COOH$ et de butan$-1-\text{ol}\,C_{4}H_{9}OH$ auquel on ajoute quelque gouttes d'acide sulfurique concentré le mélange est réparti sur $7$ tubes à essai contenant initialement chacun $a=1.33\cdot10^{-2}$ môle d'acide éthanoique et a môle de butin$-1-\text{ol}.$

On introduit les tubes dans un bain marie à la température $60^{\circ}C$ et on déclenche simultanément un chronomètre.

A chaque instant $t$, un tube est retiré du bain marie puis refroidi par l'eau glacée afin de le doser par une solution d'hydroxyde de sodium $NaOH$ de concentration molaire $C_{B}=1mol\cdot L^{-1}.$

1) Écrire l'équation de la réaction d'estérification.

2) Dresser le tableau d'avancement correspondant.

3) a) Exprimer, à une date $t$, l'avancement $x$ en fonction de $a$, $C_{B}$ et $V_{BE}$ $(V_{BE}$ volume de base ajouté à l'équivalence.$)$

b) Définir le taux d'avancement final $\tau_{f}$ d'une réaction chimique.

4) On définit le rapport $R=\dfrac{x}{a}$ à une date $t$ et on donne le tableau suivant :

$$\begin{array}{|c|c|c|c|c|c|c|c|} \hline t(min)&0&3&6&15&30&45&60\\ \hline R&0&0.44&0.58&0.64&0.67&0.67&0.67\\ \hline \end{array}$$

a) Que peut - on dire quant à l'état du système chimique à partir de la date $t=30\,min$ ?

Donner le taux d'avancement final $\tau_{f}$ de la réaction à l'équilibre dynamique.

b) Déduire, à partir du tableau, deux caractères de la réaction.

c) Énoncer la loi d'action de masse.

Exprimer la constante d'équilibre $K$ en fonction de $\tau_{f}$ puis calculer sa valeur.

d) Déterminer, en nombre de môle, la composition du mélange à la date $t=30\,min$ puis déduire le volume $V_{BE}$ versé à cette date.

5) Le système chimique est en équilibre dynamique, on ajoute $b$ môles de l'ester obtenue à volume sensiblement constant.

Quel est le sens d'évolution spontanée de la réaction ?

Justifier la réponse par deux méthodes.

Exercice 8

1. Écrire la formule semi-développée du pentan$-1-$ol et indiquer sa classe.

2. Écrire l'équation-bilan de la réaction, donner le nom de cette réaction et celui de l'ester formé.

3. On réalise, à température ordinaire un mélange équimolaire d'alcool et d'acide à raison de $0.2\,mol$ de chaque constituant. Le volume total est alors $30\,cm^{3}.$ Ce mélange est également réparti dans différents tubes que l'on plonge ensemble dans de l'eau bouillante tout en déclenchant le chronomètre.

a) A différents instants, on sort un tube que l'on plonge dans de l'eau glacée et on dose l'acide restant avec une solution d'hydroxyde de sodium de concentration molaire égale à $1\,mol\cdot L^{-1}$ dont il faut verser $V$ $cm^{3}.$

Trouver la relation liant le nombre de moles d'ester formé et le volume $V$ de base versé. Sachant que chaque tube contient $3\,cm^{3}$ de mélange, montrer que ce nombre de moles rapporté à une mole d'acide initial est lié numériquement à $V$ par la relation :

$$n_{E}=1-\dfrac{V}{20}\ ;\ V\text{ en }cm^{3}$$

b) Compléter le tableau suivant :

$$\begin{array}{|l|c|c|c|c|c|c|} \hline t(min)&3&8&13&18&28&38\\ \hline V(cm^{3})&12.9&9.5&8&7.8&6.8&6.7\\ \hline n_{E}(mol)& & & & && \\ \hline \end{array}$$

c) Tracer la courbe $n_{E}=f(t)$ à l'aide du tableau suivant.

Échelle : $5\,cm\ \rightarrow\ 10\,min$ et $5\,cm\ \rightarrow\ 0.2\,mol$

4. Déterminer graphiquement la vitesse de formation de l'ester à l'instant $t=3\,min$ puis au temps de demi-réaction.

5. Pourquoi plonge-t-on les tubes dans l'eau bouillante ?

Quel est le rôle du facteur cinétique, dû à la plongée des tubes dans l'eau bouillante, sur la vitesse de formation de l'ester ?

6. La limite de la réaction dépend-elle de ce facteur cinétique ?

Déterminer alors la composition du système final obtenu.

Exercice 9

Au laboratoire on se propose d'étudier la cinétique de la réaction de saponification du benzoate de $1-$méthyléthyle de formule semi-développée $C_{6}H_{5}-CO_{2}-CH(CH_{3})_{2}$ par l'hydroxyde de sodium. Pour cela, à une date prise comme origine des temps $t=0$, on mélange $100\,mL$ d'une solution de benzoate de $1-$méthyléthyle de concentration égale à $0.1\,mol\cdot L^{-1}$ et $100\,mL$ d'une solution d'hydroxyde de sodium de concentration égale à $0.1\,mol\cdot L^{-1}.$ Le mélange est maintenu à $50^{\circ}C$, sous agitation permanente. On prélève à différentes dates $t$, un volume $v=10\,mL$ de ce mélange. Chaque prélèvement est aussitôt versé dans un erlenmeyer contenant de l'eau glacée et on dose la quantité d'hydroxyde de sodium restante à l'aide d'une solution aqueuse d'acide chlorhydrique de concentration $C_{a}=2\cdot10^{-2}mol\cdot L^{-1}$, l'indicateur coloré étant le bleu de bromothymol.

1. Montrer que la concentration initiale $[OH^{-}]_{0}$ des ions $OH^{-}$ dans le mélange est de $5\cdot10^{-2}mol\cdot L^{-1}.$

2. Écrire l'équation-bilan de la réaction chimique support du dosage. Préciser la couleur de la solution obtenue à l'équivalence.

3. Écrire l'équation-bilan de la réaction entre le benzoate de $1-$méthyléthyle et l'hydroxyde de sodium, et préciser ses caractéristiques.

4. Les résultats du dosage sont regroupés dans le tableau suivant, $V_{a}$ étant le volume d'acide versé à l'équivalence du dosage d'un prélèvement et $C$ la concentration de l'alcool formé.

$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|c|c|} \hline t(min)&0&4&8&12&16&20&24&28&32&36&40\\ \hline V_{a}(mL)&&22.0&19.8&18.0&16.5&15.0&13.8&12.8&12.0&11.5&11.0\\ \hline C\left(10^{-3}mol\cdot L^{-1}\right)&0& & & & &&&&&& \\ \hline \end{array}$$

a) Montrer que la concentration de l'alcool dans le prélèvement est donnée par l'expression :

$$C=\left[OH^{-}\right]_{0}-\dfrac{C_{a}V_{a}}{v}$$

b) Recopier puis compléter le tableau. Tracer le graphe $C=f(t)$ avec les échelles suivantes :

$1\,cm$ pour $4\,min$ ; $2\,cm$ pour $4\cdot10^{-3}mol\cdot L^{-1}$

c) Définir la vitesse volumique instantanée de formation de l'alcool et déterminer sa valeur à $t_{1}=4\,min$ et à $t_{2}=32\,min.$

Justifier l'évolution constatée pour cette vitesse.

d) On reprend la même étude à $30^{\circ}C$, les valeurs du volume $V_{a}$ mesurées pour les mêmes dates sont-elles plus grandes ou plus petites qu'à $50^{\circ}C$ ?

Justifier la réponse.

Exercice 10

On dissout $10^{-2}$ mol de $2-$méthylbutanoate de méthyle dans la quantité d'eau nécessaire pour obtenir un litre de solution.

2.1 Donner la formule semi-développée du $2-$méthylbutanoate de méthyle.

Quelle est sa fonction chimique ? Donner son groupe fonctionnel.

2.2 Écrire l'équation-bilan de la réaction d'hydrolyse du $2-$méthylbutanoate de méthyle. Préciser le nom et la fonction chimique de chaque produit obtenu.

2.3 On prélève $100\,mL$ de la solution précédente qu'on répartit dans $10$ tubes. A la date $t=0$ tous les tubes contiennent le même volume de cette solution. Pour déterminer le nombre de moles d'ester restant $n_{E}$ à une date $t$, on prélève un tube qu'on met dans la glace puis on dose l'acide formé à l'aide d'une solution d'hydroxyde de sodium de concentration molaire $C_{b}=10^{-2}mol\cdot L^{-1}$ en présence d'un indicateur coloré. On obtient les résultats suivants :

$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|} \hline t(min)&0&10&20&30&40&50&60&90&120\\ \hline V_{b}(mL)&0&2.1&3.7&5&6.1&6.9&7.5&8.6&9.4\\ \hline n_{E}\left(10^{-5}mol\right)& & & & &&&&& \\ \hline \end{array}$$

$V_{b}$ est le volume d'hydroxyde de sodium à l'instant de date considéré.

a) Montrer que $n_{E}=10^{-5}(10-V_{b}).$ $V_{b}$ en $mL.$

b) Recopier et compléter le tableau ci-dessus puis tracer la courbe représentative de la quantité d'ester restant au cours du temps $n_{E}=f(t).$

Échelle : $1\,cm\ \rightarrow\ 10\,min$ et $1.5\,cm\ \rightarrow\ 10^{-5}mol$

c) Définir le temps de demi-réaction puis le déterminer.

d) Définir la vitesse instantanée de disparition de l'ester puis la déterminer à la date $t=40\,min.$

Exercice 11

On oxyde à la date $t=0$ un volume $V_{1}=100\,mL$ d'une solution d'iodure de potassium $(K^{+}+I^{-})$ de concentration $C_{1}=4.64\cdot10^{-2}mol/L$ par un volume $V_{2}=100\,mL$ d'une solution $S_{2}$ d'eau oxygénée $H_{2}O_{2}$ de concentration $C_{2}=4\cdot10^{-2}mol/L.$ On ajoute à ce mélange un volume négligeable d'acide sulfurique très concentré.

1. Donner les couples redox mis en jeu et écrire l'équation de la réaction.

Calculer à la date $t=0$ la concentration de $I^{-}$ et celle de $H_{2}O_{2}$ dans le mélange. Lequel des deux réactifs est en excès ?

2. On détermine à différents instants la concentration du diiode formé, on obtient la courbe ci-dessus.

3.1. Calculer la vitesse moyenne de formation du diiode entre les instants $t_{1}=5\,min$ et $t_{2}=20\,min.$

3.2. Définir la vitesse instantanée de formation de $I_{2}$ et la calculer à la date $t=12.5\,min.$

En déduire la vitesse de disparition de $I^{-}$ à cette date. Comment évolue ces vitesses en fonction du temps ?

Quel est le facteur cinétique responsable ?

3.3. Calculer la concentration des ions $I^{-}$ et de $H_{2}O_{2}$ présents dans le mélange réactionnel à $t=30\,min.$

3. Déterminer le temps de demi-réaction.

Exercice 12

On étudie la cinétique chimique de l'oxydation d'une solution d'oxalate de sodium $\left(2Na^{+}+C_{2}O_{4}^{2-}\right)$ à l'aide d'une solution de permanganate de potassium $(K^{+}+MnO_{4}^{-})$ en utilisant des volumes égaux des deux solutions mais de concentrations respectives $C_{1}=0.6mol\cdot L^{-1}$ et $C_{2}=0.2\,mol\cdot L^{-1}.$

1. Écrire les demi-équations et en déduire l'équation-bilan.

On donne :

$E^{\circ}\left(MnO_{4}^{-}/Mn^{2+}\right)=1.51V$ et $E^{\circ}\left(CO_{2}/C_{2}O_{4}^{2-}\right)=0.48V.$

2. Calculer à $t=0$ les concentrations molaires volumiques $\left[MnO_{4}^{-}\right]_{0}$ et $\left[C_{2}O_{4}^{2-}\right]_{0}.$

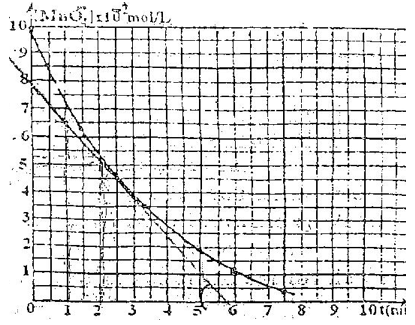
3. La courbe ci-dessous représente la variation de la concentration de $MnO_{4}^{-}$ en fonction du temps.

3.1. Définir et calculer la vitesse moyenne de disparition entre les instants $t_{1}=2\,min$ et $t_{2}=5\,min$

3.2. Définir et calculer la vitesse de disparition de $MnO_{4}^{-}$ à l'instant $t=2.5\,min$ et en déduire la vitesse de formation de $CO_{2}$ au même instant.

4. Définir et déterminer le temps de demi-réaction

4.1. Ce résultat est-il en accord avec la courbe ?

Déterminer le temps de demi-réaction $t_{\dfrac{1}{2}}$

4.2. Déterminer la concentration du diiode lorsqu'il restera le quart de l'eau oxygénée.