Étude expérimentale des lentilles minces - 1er s
Classe:
Première
Les lentilles sont des objets transparents que l'on trouve dans des appareils courants : lunettes, verres de contacts, appareil de photo, microscope, lunette astronomique...
Dans tous les cas, leur rôle est d'obtenir des images d'objets que l'on désire observer.
I. Lentille mince convergente-Lentille mince divergente
1. Description
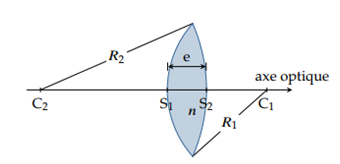
Une lentille est un milieu transparent, homogène limité par deux faces sphériques ou une face sphérique et une face planee $≪R_{1}\ e≪R_{2}\text{ et }e≪C_{1}C_{2}$
On appelle lentille mince, une lentille pour laquelle l'épaisseur est relativement petite par rapport au rayon de courbure.
2. Classification des lentilles
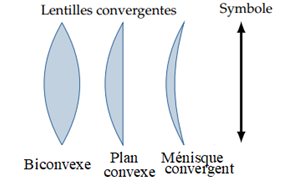
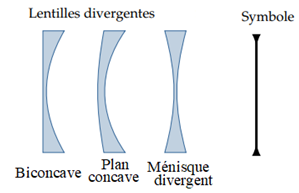
On distingue deux types de lentilles :
$\bullet\ $les lentilles à bords minces qui sont convergentes,
$\bullet\ $les lentilles à bords épais qui sont divergentes
3. Caractéristiques des lentilles
3.1. Axe optique principal
C'est la droite passant par $O$ et par le centre de courbure d'une des faces sphériques.
C'est l'axe de symétrie de la lentille.
Par convention, on oriente l'axe optique dans le sens de propagation de la lumière et on choisit pour origine le centre optique $O.$
3.2. Centre optique.
Le point O est appelé centre optique de la lentille.
Pour les lentilles que nous utiliserons $O$ est le centre géométrique
3.3. Foyer objet et foyer image
Deux points jouent un rôle particulier dans les lentilles : il s'agit des foyers objet et image.
3.3.1. Foyer image
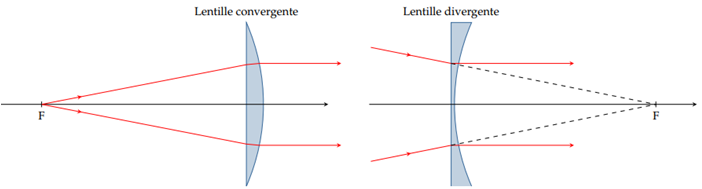
Par définition, l'image d'un point à l'infini sur l'axe est le foyer image $F^{\prime}.$
Dans le cas d'une lentille convergente, le foyer image est réel alors qu'il a le statut d'image virtuelle pour une lentille divergente.
De façon analogue, on définit la distance focale objet :
La distance qui sépare le centre $O$ du foyer image $F^{\prime}$ est la distance focale objet.
C'est une grandeur algébrique $f^{\prime}=\overline{OF}\succ 0.$
Son unité est le mètre
3.3.2. Foyer objet
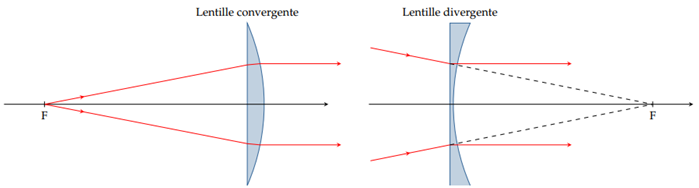
Par définition, un objet lumineux placé au foyer objet $F$ aura pour image un point à l'infini sur l'axe.
Dans le cas d'une lentille convergente, le foyer objet est réel alors qu'il a le statut d'objet virtuel pour une lentille divergente.
De façon analogue, on définit la distance focale objet :
La distance qui sépare le centre $O$ du foyer objet $F$ est la distance focale objet.
C'est une grandeur algébrique $f=\overline{OF}\prec 0.$
Son unité est le mètre
On montre que dans le cas des lentilles minces dont les milieux extrêmes sont identiques :
$$f=\overline{OF}=-\overline{OF}=-f^{\prime}$$
3.4. Plan focal objet et Plan focal image
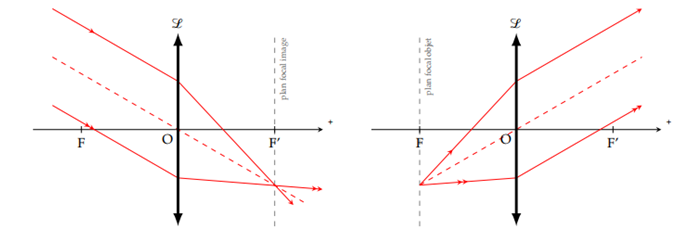
Le plan focal objet : est le plan perpendiculaire à l'axe optique et contenant le foyer objet $F.$
Le plan focal image : est le plan perpendiculaire à l'axe optique et contenant le foyer image $F^{\prime}$
3.5. Vergence.
Pour quantifier la capacité à faire converger les rayons on définit la vergence d'une lentille.
La vergence est égale à l'inverse de $f^{\prime}$ et s'exprime en dioptries
$$\boxed{C=\dfrac{1}{f^{\prime}}}$$
$f^{\prime}$ en mètre $(m)$
$C$ en dioptrie $$(\delta)$
Une lentille est d'autant plus convergente que sa vergence est grande

Commentaires
Anonyme (non vérifié)
lun, 02/26/2024 - 23:40
Permalien
S'intéresse ces cours
Anonyme (non vérifié)
lun, 02/26/2024 - 23:40
Permalien
S'intéresse ces cours
Rassidou Kande (non vérifié)
lun, 02/26/2024 - 23:44
Permalien
Reçois la contenue
Ajouter un commentaire