Corrigé BFEM Physique chimie 2010
Exercice 1
Un briquet neuf rempli de gaz butane $(C_{4}H_{10})$ a une masse de $14.8\;g$ Utilisé pendant quelques jours, le briquet est vidé de son contenu ; sa masse est alors $9\;g.$ Tout le butane a réagi avec le dioxygène de l'air et la combustion est supposée complète.
1.1) Écrivons l'équation bilan de la complète du butane
$$C_{4}H_{10}\ +\ \dfrac{13}{2}O_{2}\ \longrightarrow\ 4CO_{2}\ +\ 5H_{2}O$$
1.2) Calculons la quantité de matière de butane brulée
Soit : $n_{(C_{4}H_{10})}=\dfrac{m_{(C_{4}H_{10})}}{M_{(C_{4}H_{10})}}$
Avec,
$\begin{array}{rcl} m_{(C_{4}H_{10})}&=&m_{(\text{briquet neuf})}-m_{(\text{briquet vide)}}\\\\&=&14.8-9\\\\&=&5.8\end{array}$
Donc, $m_{(C_{4}H_{10})}=5.8\;g$
$\begin{array}{rcl} M_{(C_{4}H_{10})}&=&4M_{(C)}+10M_{(H)}\\\\&=&4\times 12+10\times 1\\\\&=&48+10\\\\&=&58\end{array}$
Donc, $M_{(C_{4}H_{10})}=58\;g.mol^{-1}$
Ainsi, en remplaçant ces valeurs de $m_{(C_{4}H_{10})}$ et de $M_{(C_{4}H_{10})}$, on obtient :
$n_{(C_{4}H_{10})}=\dfrac{5.8}{58}=0.1$
D'où, $$\boxed{n_{(C_{4}H_{10})}=0.1\;mol}$$
1.3) Déduisons en le volume de dioxygène nécessaire à cette combustion
On a : $n_{(O_{2})}=\dfrac{V_{(O_{2})}}{V_{M}}\ \Rightarrow\ V_{(O_{2})}=n_{(O_{2})}\times V_{M}$
Or, d'après l'équation bilan, on a : $\dfrac{n_{(C_{4}H_{10})}}{1}=\dfrac{n_{(O_{2})}}{\dfrac{13}{2}}$
Ce qui donne alors : $n_{(O_{2})}=\dfrac{13\times n_{(C_{4}H_{10})}}{2}$
En remplaçant cette expression de $n_{(O_{2})}$ dans l'expression de $V_{(O_{2})}$, on obtient :
$\boxed{V_{(O_{2})}=\dfrac{13\times n_{(C_{4}H_{10})}\times V_{M}}{2}}$
A.N : $V(O_{2})=\dfrac{13\times 0.1\times 24}{2}=15.6$
Ainsi, $$\boxed{V_{(O_{2})}=15.6\;L}$$
1.4) La combustion d'une mole de gaz butane libère une quantité de chaleur de $2\,800\;kJ.$
Calculons alors la quantité de chaleur $Q$ libérée par $0.1\;mol$ de gaz butane
Comme $1\;mol$ libère $2\,800\;kJ$ alors, $0.1\;mol$ va libérer $Q=0.1\times 2\,800=280$
Donc, $$\boxed{Q=280\;kJ}$$
Exercice 2
On dispose d'une solution d'acide chlorhydrique $(H^{+}+Cl^{-})$ de concentration molaire $C_{a}$ inconnue.
2.1) On prélève quelques millilitres de la solution que l'on introduit dans un tube à essais contenant de la grenaille de zinc. Il se produit une réaction chimique et on observe un dégagement gazeux. En approchant une flamme au dessus de l'ouverture du tube, on entend une petite explosion.
2.1.1) Le gaz qui se dégage est du dihydrogène. Sa formule est $H_{2}.$
2.1.2) Écrivons l'équation bilan de la réaction entre les ions $H^{+}$ et les atomes de zinc
$$(H^{+}+Cl^{-})\ +\ Zn\ \longrightarrow\ (Zn^{2+}+2Cl^{-})\ +\ H_{2}$$
2.2) On prélève à nouveau $10\;mL$ de la solution d'acide que l'on met dans un bêcher, on y ajoute quelques gouttes de bleu de bromothymol $(BBT).$ On dose alors l'acide par une solution d'hydroxyde de sodium $(Na^{+}+OH^{-})$ de concentration molaire $C_{b}=5\cdot 10^{-2}\;mol.L^{-1}$ Le volume de base versé à l'équivalence est $V_{b}=20\;mL.$
2.2.1) On peut affirmer que l'équivalence est atteinte lorsqu'on observe un premier changement de couleur de l'indicateur ; c'est-à-dire lorsque le BBT change de couleur en passant du jaune au verte.
2.2.2) Déterminons la concentration $C_{a}$ de la solution d'acide
A l'équivalence, on a : $n_{a}=n_{b}$
Or, $n_{a}=C_{a}\times V_{a}\ $ et $\ n_{b}=C_{b}\times V_{b}$
Donc, $C_{a}\times V_{a}=C_{b}\times V_{b}$
Par suite, $C_{a}=\dfrac{C_{b}\times V_{b}}{V_{a}}$
A.N : $C_{a}=\dfrac{5\cdot 10^{-2}\times 20}{10}=0.1$
D'où, $$\boxed{C_{a}=0.1\;mol.L^{-1}}$$
Exercice 3
On a mesuré la résistance de deux fils cylindriques, de même section $S$, mais de métaux différents. Les résultats obtenus sont regroupés dans le tableau ci-après.
$$\begin{array}{|c|c|c|}\hline\text{Métal}&\text{Longueur du fil en }(m)&\text{Résistance du fil en }(\Omega)\\ \hline\text{Aluminium}&10&7.8\\ \hline\text{Cuivre}&50&25\\ \hline\end{array}$$
3.1) Calculons pour chaque fil la résistance pour une longueur de $100\;m$
$-\ $ Pour l'aluminium :
$10\;m$ correspond à $7.8\;\Omega$ donc, pour chaque mètre on obtient : $\dfrac{7.8}{10}=0.78\;\Omega$
Ainsi, la résistance d'un fil en aluminium de longueur $100\;m$ sera donnée par :
$R_{A}=0.78\times 100=78$
D'où, $$\boxed{R_{A}=78\;\Omega}$$
$-\ $ Pour le cuivre :
$50\;m$ correspond à $25\;\Omega$ donc, pour chaque mètre on obtient : $\dfrac{25}{50}=0.5\;\Omega$
Ainsi, la résistance d'un fil en cuivre de longueur $100\;m$ est donnée par :
$R_{C}=0.5\times 100=50$
D'où, $$\boxed{R_{C}=50\;\Omega}$$
3.2) Le cuivre est le métal de résistance inférieure, alors il est meilleur conducteur électrique.
3.3) Calculons la valeur de la section $S$ des fils sachant que la résistivité du cuivre vaut $\rho=1.8\;10^{-8}\;\Omega.m$
On a : $R=\dfrac{\rho\times \ell}{S}$
Donc, $R\times S=\rho\times \ell$
Par suite, $S=\dfrac{\rho\times \ell}{R}$
A.N : $S=\dfrac{1.8\cdot10^{-8}\times 100}{50}$
Ainsi, $$\boxed{S=3.6\cdot10^{-8}\;m^{2}}$$
Exercice 4
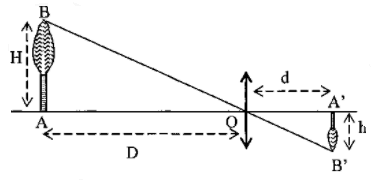
Considérons le schéma ci-dessous. L'objectif de l'appareil sera assimilé à une lentille convergente de distance focale $50\;mm.$

4.1) Calculons la vergence de cette lentille
Soit : $C=\dfrac{1}{f}$
A.N : $C=\dfrac{1}{50\cdot10^{-3}}=20$
Donc, $$\boxed{C=20\;\delta}$$
4.2.1) Donnons les caractéristiques de l'image
$-\ $ nature : réelle
$-\ $ sens : renversé
$-\ $ position : de l'autre côté de la lentille
$-\ $ taille : plus petite que l'objet
4.2.2) Le groupe d'élèves calcule la hauteur de l'arbre à partir de la relation :
$$H=\dfrac{Dh}{d}$$
a) Retrouvons cette relation à partir du schéma
Comme les triangles $ABO\ $ et $\ A'B'O$ sont en position de Thalès alors, en appliquant le théorème de Thalès, on obtient :
$$\dfrac{OA'}{OA}=\dfrac{A'B'}{AB}$$
Or, $AB=H\;;\ OA=D\;;\ A'B'=h\ $ et $\ OA'=d$
Ainsi, en remplaçant, on trouve :
$$\dfrac{d}{D}=\dfrac{h}{H}$$
Par suite, $H\times d=D\times h$
D'où, $$\boxed{H=\dfrac{D\times h}{d}}$$
b) Calculons la hauteur $H$ de l'arbre
On a : $H=\dfrac{D\times h}{d}$
A.N : $H=\dfrac{10\times 1.5\cdot10^{-2}}{50.2\cdot10^{-3}}=3$
Donc, $$\boxed{H=3\;m}$$
Auteur:
Aliou ndiaye

Commentaires
MOUHAMED POUYE (non vérifié)
mer, 06/16/2021 - 19:09
Permalien
demande
Anonyme (non vérifié)
ven, 06/28/2024 - 08:38
Permalien
Bonne
Anonyme (non vérifié)
ven, 06/28/2024 - 08:40
Permalien
C'est une application
Ajouter un commentaire