BFEM Mathématiques 1er groupe - 2023

Exercice 1

Pour chacune des questions dans le tableau ci-dessous, trois réponses $A$, $B$ et $C$ sont proposées dont une seule est correcte.

Pour répondre, tu porteras sur ta copie, le numéros de la question suivi de la lettre correspondant à la réponses choisie.

Chaque réponse correcte est notée $0.75$ points.

Une réponse fausse ou une absence de réponse est notée $0$ point.

$\begin{array}{|c|l|c|c|c|} \hline N^{\circ}&\text{Questions}&\text{Réponse }A&\text{Réponse }B&\text{Réponse }C\\\hline 1&\text{Quelle est la valeur du réel }\dfrac{5}{6}\sqrt{\dfrac{36}{5}}\ ?&\dfrac{1}{6}\sqrt{36}&\sqrt{6}&\sqrt{5}\\ \hline &\text{Quels sont les réels qui vérifient l'équation}&-1-\sqrt{3}&1-\sqrt{3}&1+\sqrt{3}\\ 2&&\text{et}&\text{et}&\text{et}\\ &\sqrt{(2x+7)^{2}}=|5-2\sqrt{3}|\ ?&-6+\sqrt{3}&6+\sqrt{3}&6-\sqrt{3}\\ \hline &\text{Quelle est l'aire latérale en }cm^{2}text{ d'un cône de}&&&\\3&\text{révolution de rayon de base }r=2\sqrt{2}\,cm&12\pi&4\sqrt{6}\pi&36\sqrt{2}\pi\\&\text{et de génératrice }g=\sqrt{18}\,cm\ ? &&&\\ \hline &\text{On considère la série statistique de note suivante :}&&&\\ 4&17\ ;\ 9\ ;\ 11\ ;\ 6\ ;\ 13\ ;\ 18\ ;\ 13\ ;\ 15\ ;\ 14\ ;\ 13&14&13&15\\ &\text{Quelle est la note médiane ?}&&&\\\hline &\text{soit }ABC\text{ un triangle tel que }&&&\\&\widehat{CAB}=55^{\circ}\text{ et }\widehat{CBA}=80^{\circ}&&&\\5&\text{Soit }O\text{ le centre du cercle circonscrit au triangle et}&90^{\circ}&45^{\circ}&55^{\circ}\\&P\text{ le point diamétralement opposé à }B&&&\\&\text{Quelle est la mesure de l'angle }\widehat{AOB}\ ?&&&\\ \hline&\text{Quelle est l'expresion littérale}&&&\\ 6&\text{de l'application affine }g\text{ telle que}&2x+3&-2x-3&-2x+3\\& g\left(\dfrac{1}{2}\right)=2\text{ et }g(1)=1\ ?&&&\\ \hline &\text{Quel est le vecteur égal à}&&&\\ 7&&\overrightarrow{2AE}&\overrightarrow{O}&\dfrac{1}{2}\overrightarrow{AE}\\&\overrightarrow{U}=\overrightarrow{GA}-\overrightarrow{EM}-\overrightarrow{GF}+\overrightarrow{EF}+ \overrightarrow{AM}\ ?&&&\\\hline &\text{Soit }ABC\text{ un triangle équilatéral}&&&\\8&\text{de côté }\alpha\text{ et de hauteur }h&\alpha\dfrac{\sqrt{3}}{2}&\alpha\sqrt{3}&\alpha\dfrac{\sqrt{2}}{3}\\ &\text{Quelle est la valeur de la hauteur }h\ ?&&&\\ \hline &\text{Quel est l'ensemble des soutions}&&&\\9&\text{dans }\mathbb{R}\text{ de l'inéquation}&\left[-\dfrac{3}{2}\;,\ 3\right]&\left]-\dfrac{3}{2} \;,\ 3\right[&\left\lbrace-\dfrac{3}{2}\;,\ 3\right\rbrace\\&(3-x)(2x+3)>0\ ?&&&\\ \hline &\text{Soit }ABC\text{ un triangle Inscrit dans un cercle}&&&\\ 10&\text{de centre }O\text{ tel que }\widehat{OAC}=55^{\circ}&55^{\circ}&110^{\circ}&35^{\circ}\\&\text{Quelle est la mesure de l'angle }\widehat{ABC}\ ?&&&\\\hline \end{array}$

Exercice 2

1. Écris l'expression $E=\sqrt{\left(3-3\sqrt{2}\right)^{2}}+\sqrt{50}-7\sqrt{32}+\sqrt{9}$ sous la la forme $a\sqrt{b}$ avec $a$ et $b$ des entiers relatifs, $b$ positif.

2. On pose relatifs, $p=\dfrac{2\sqrt{3}-2}{\sqrt{3}+2}$ et $q=\dfrac{1}{6\sqrt{3}-10}$

Montre que $p$ et $q$ sont des inverses.

3. On considère des réels $x$ t $y$ tels que $x=6\sqrt{3}-10$ et $y=\sqrt{208-120\sqrt{3}}$

a. Détermine le signe $x$

b. Calcule $x^{2}$;

Déduis-en une écriture simplifiée de $y=\sqrt{208-120\sqrt{3}}$

c. Encadre le réel $x$ à $10^{-2}$ près sachant que $1.732<\sqrt{3}<1.733$

Exercice 3 :

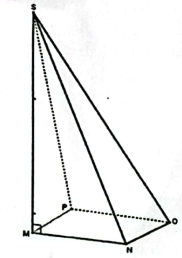
La figure $SMNOP$ ci-contre représente une pyramide à base rectangulaire $MNOP$, de hauteur $[SM]$.

On donne: $SM=7.5\,cm$ ;

$MN=4\,cm$ et

$NO=5.5\,cm$

1. Calcule le volume $V_{1}$ de la pyramide $SMNOP$

2. Montre que $SN=8.5\,cm$

3. Soit $I$ un point de $[SM]$ tel que $SI=6\,cm$ et $j$ celui de $[SN]$ tel que $SJ=6.8\,cm$

a. Montre que les droits $(IJ)$ et $(MN)$ sont parallèles.

b. Calcule la longueur $IJ$

4. Le plan passant par $I$ et parallèle à la base de la pyramide

$SMNOP$ coupe les segments $[SO]$ et $[SP]$ respectivement aux points $K$ et $L$

Calcule le volume du solide $SIJKL$

5. Un menuisier métallique veut fabriquer un récipient pou servir d'unité de mesure d'un produit céréalier qu'on doit distribuer aux populations d'une commune.

Ce récipient est représenté par le solide $IJKLMNOP$ à l'échelle de $\dfrac{1}{5}$

a. Sachant qu'un $kg$ de ce produit occupe un volume de volume de $1400\,cm^{3}$, détermine à $1\,g$ prés par défaut la quantité maximale en grammes de ce produit que peut contenir ce récipient

b. Le menuisier souhaiterait inscrire le nom de la commune sur la face $MNJI$ du récipient.

Pour cela, il doit d'abord couvrir cette face de la feuille d'aluminium lisse.

Sachant que $10\,cm^{2}$ de feuille d'aluminium lisse coûtent $150$ francs, calcule la dépense minimale en feuille d'aluminium lisse.