Exercice 1

1. On considère les réels suivants :

$A=(2-\sqrt{5})(2+\sqrt{5})^{2}$ ;

$B=3\sqrt{12}-\dfrac{1}{2}\sqrt{108}-\sqrt{8}\times\sqrt{2}$ ;

$a=-3\sqrt{3}+4$ ;

$b=-2-\sqrt{5}$ ;

$c=2+\sqrt{5}$ ;

$d=3\sqrt{3}-4.$

Parmi les réels $a$, $b$, $c$ et $d$ indique celui qui est égal à $A$ et celui qui est égal à $B.$

2. On donne :

$x=\dfrac{-1}{3-2\sqrt{2}}$ ;

$y=\sqrt{\dfrac{1}{2}}-\sqrt{\dfrac{3}{2}}$ ;

$z=\sqrt{\dfrac{1}{2}}+\sqrt{\dfrac{3}{2}}.$

a) Montre que $x=-3-2\sqrt{2}.$

b) Donne un encadrement de $x$ à $10^{-1}$ près sachant que $1.414<\sqrt{2}<1.415.$

c) Calcule $y^{2}$ et $z^{2}.$

d) Déduis de la question précédente que $\sqrt{2-\sqrt{3}}+\sqrt{2+\sqrt{3}}=\sqrt{6}.$

Exercice 2

1. On considère l'équation suivante : $0.2y-\dfrac{1}{5}x=0.8.$

Parmi les couples suivants, trouve qui sont solutions de l'équation précédente.

a) $(0\ ;\ -1)$

b) $\left(0.5\ ;\ \dfrac{9}{2}\right)$

c) $(\pi\ ;\ 7.14)$

d) $\left(-\dfrac{6}{7}\ ;\ \dfrac{22}{7}\right)$

2. Résous dans $\mathbb{R}^{2}$ le système d'équations suivant :

$$\left\lbrace\begin{array}{lcl} x-y+4&=&0\\\\x-\dfrac{3}{5}y&=&0 \end{array}\right.$$

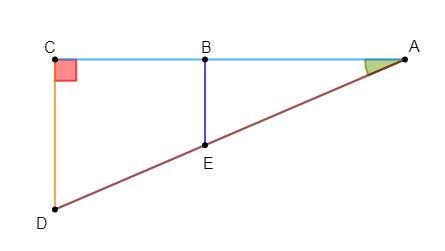
3. Dans la figure ci-dessous, $ACD$ est un triangle rectangle en $C$ et $(BE)$ est parallèle à $(CD).$

On donne : $BC=4\;;\ CD=5\;;\ BE=3$

On pose : $AB=m\ $ et $\ AC=n$

a) Montre que les réels $m$ et $n$ vérifient le système d'équations :

$$\left\lbrace\begin{array}{lcl} n&=&m+4\\5m-3n&=&0 \end{array}\right.$$

b) Calcule $m$ et $n.$

c) Calcule le cosinus de l'angle $\widehat{BAE}$

Exercice 3

1. Le dessin ci-dessous est une représentation en perspective cavalière d'un solide.

a) Indique le nom du solide qu'il représente.

b) Que représente le segment $[SO]$ pour ce solide ?

c) Que représente le segment $[SA]$ pour ce solide ?

d) Que représente le disque de rayon $[AO]$ pour ce solide ?

e) L'expression $n\times OA\times SA$ est l'aire d'une partie de ce solide.

Laquelle ?

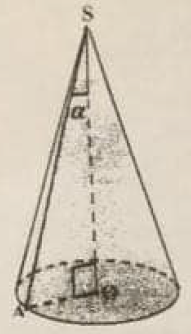
2. On donne $\alpha=30^{\circ}$ et $OA=6u$, où $u$ est une unité de mesure de longueur.

a) Justifie que le segment $[SA]$ mesure $12u$

b) Justifie que le segment $[SO]$ mesure $6\sqrt{3}u$

c) Calcule l'aire de la surface totale de ce solide en fonction de $u.$

d) Calcule le volume de ce solide en fonction de $u.$

3. Pour fabriquer un récipient qui doit contenir des sachets de jus de fruits de $30\,cl$, un groupement d'intérêt économique $[GIE]$ dispose d'un solide en matière plastique ayant la forme du solide représenté ci-dessous avec $OA=6\,dm$ et $\alpha=30^{\circ}$

On sectionne ce solide par un plan parallèle au plan de base à $4\sqrt{3}\,dm$ à partir du point $O$ pour obtenir une bassine en forme de tronc de cone.

Détermine le nombre maximale de sachets que ce récipient pourrait contenir

NB : On rappelle que $1t=1\,dm^{3}$