Solution des exercices : Les lentilles minces 3e
Classe:
Troisième
Exercice 1
1) Une lentille convergente a ses bords minces alors qu'une lentille divergente a ses bords épais.
2) Un rayon incident passant le centre optique ne subit pas de déviation alors qu'il est dévié s'il passe par les bords.
3) Une lentille convergente donne d'un objet renversé situé à 2 f une image réelle.
4) Si un objet AB est placé sur le foyer objet d'une lentille convergente, l'image obtenue est à l'infini.
5) La vergence d'une lentille est l'inverse de sa distance focale.
Exercice 2
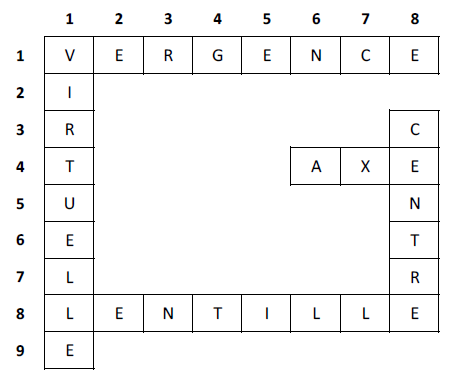
Exercice 3
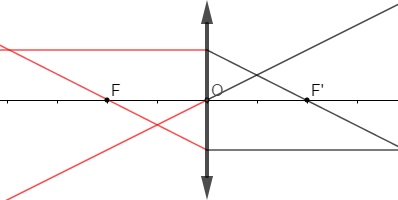
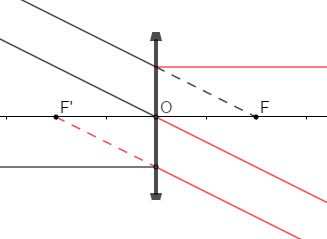
Exercice 4
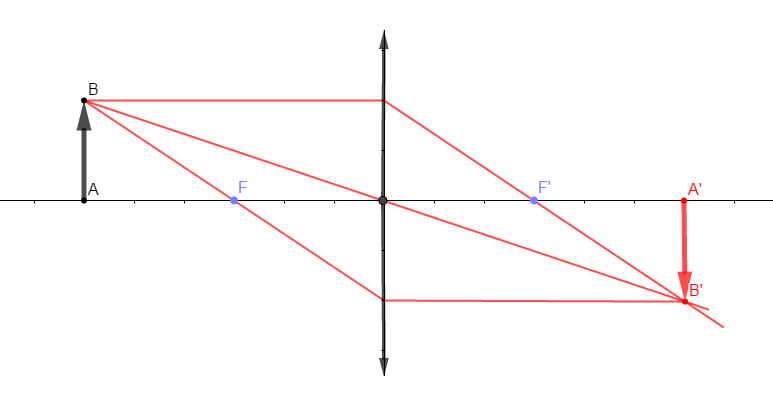
$A'$ est l'image donnée par la lentille de l'objet réel $A$.
1) Traçons les trois rayons particuliers permettant d'obtenir l'image $A'$.
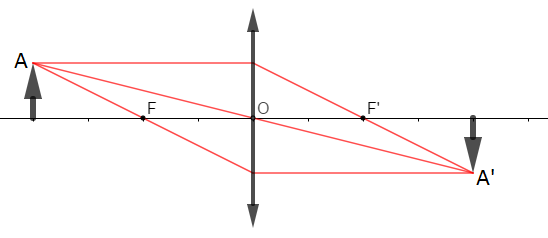
2) Caractéristiques de cette image :
$-\ $ image réelle
$-\ $ image renversée
$-\ A=A'\ :$ l'objet est égal à l'image
$-\ $ agrandissement $\gamma=\dfrac{A'}{A}=1$
$-\ $ image symétrique à l'objet par rapport au centre optique.
Exercice 5
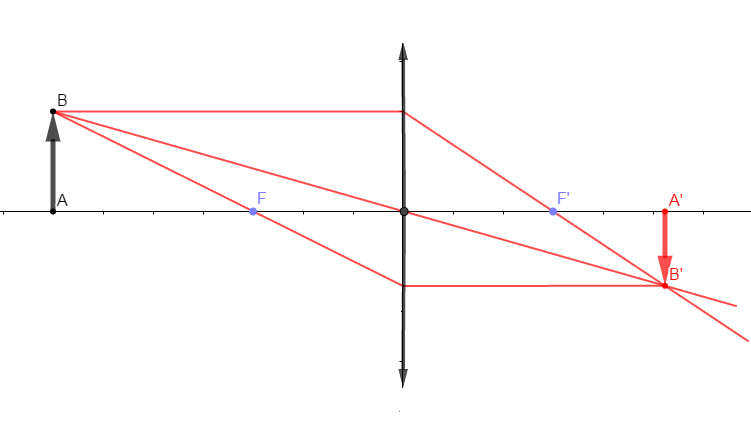
On choisit comme échelle : $1\text{carreau}\ \rightarrow\ 10\;cm$
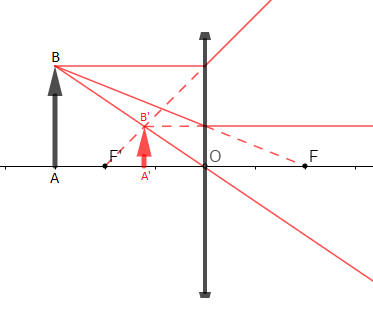
Caractéristiques de l'image :
$-\ $ image virtuelle
$-\ $ image droite
$-\ $ image plus petite que l'objet
$-\ $ agrandissement $\gamma=\dfrac{A'B'}{AB}=\dfrac{OA'}{OA}=\dfrac{12}{30}=\dfrac{4}{10}$
$-\ $ même côté par rapport à l'objet
Exercice 6
1) On choisit comme échelle : $1\text{ carreau}\ \rightarrow\ 1\;cm$
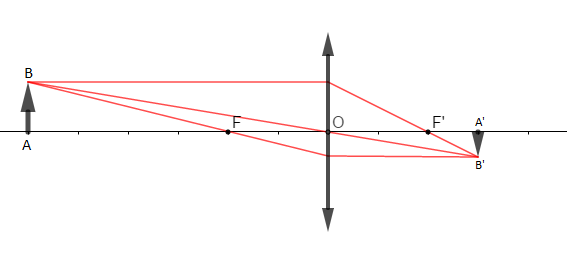
2) Caractéristiques de l'image $A'B'$ obtenue :
$-\ $ image réelle
$-\ $ image renversée
$-\ $ image plus petite que l'objet
$-\ $ agrandissement $\gamma=\dfrac{A'B'}{AB}=\dfrac{1}{2}$
$-\ $ image sur le côté opposé $OA'=\dfrac{1}{2}OA$
3) On a une lentille convergente.
Vergence : $C=\dfrac{1}{f}=\dfrac{1}{2.10^{-2}}=50\;\delta$
Exercice 7
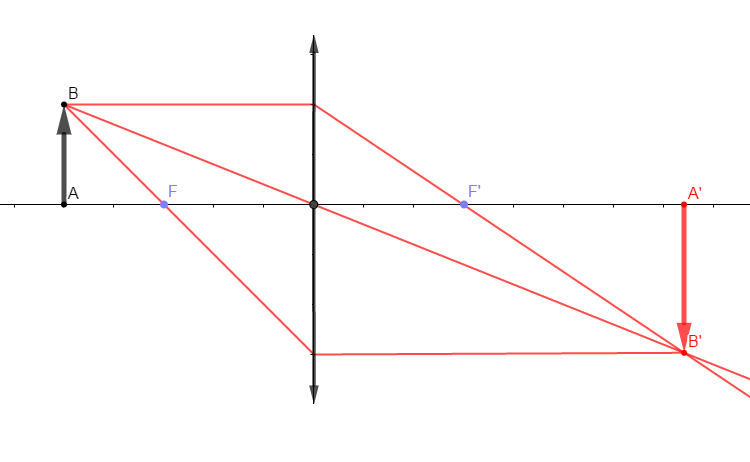
1) Trouvons, à partir du graphe, la distance focale de cette lentille.
On choisit comme échelle : $1\text{ carreau}\ \rightarrow\ 10\;cm$
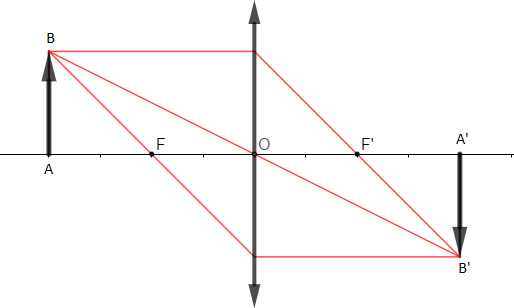
D'après l'échelle on a : $2\text{ carreaux}\ \rightarrow\ x\;cm\ \Rightarrow\ 2\times 10=x$
D'où, $\boxed{f=20\;cm}$
2) L'agrandissement de cette image est donné par :
$\gamma=\dfrac{A'B'}{AB}=\dfrac{20}{20}=1$
Donc, $A'B'=AB$
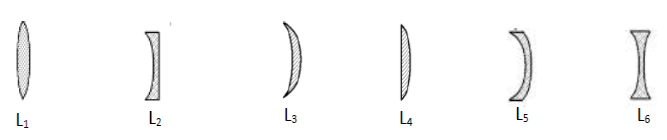
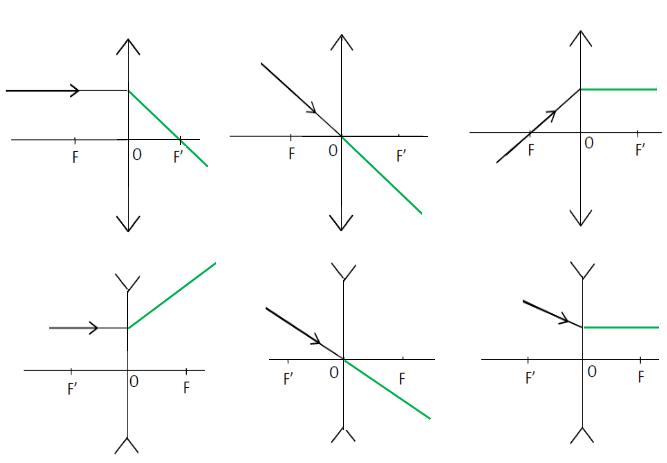
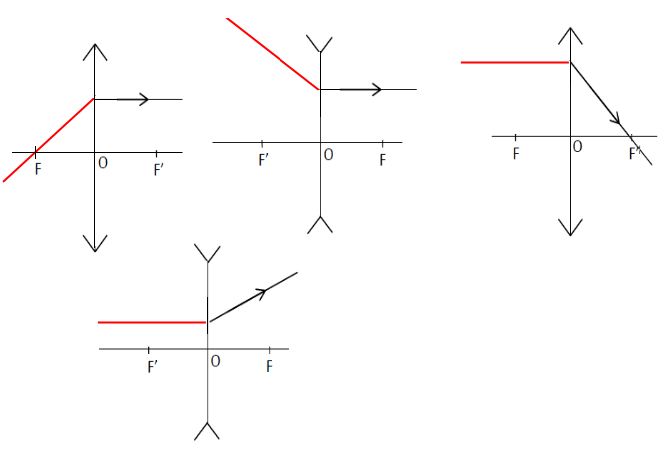
Exercice 9 : Contrôle de connaissances
1) Les deux types de lentilles sont : les lentilles convergentes et les lentilles divergentes.
2) C'est la lentille convergente qui "rabat" un faisceau incident de lumière vers l'axe optique.
3) La lentille qui ouvre le faisceau incident de lumière est appelée lentille divergente.
4) On dispose ci-dessous de six lentilles $L_{1}\;;\ L_{2}\;;\ L_{3}\;;\ L_{4}\;;\ L_{5}\ $ et $\ L_{6}$

4.1) Classifions ces lentilles en lentilles convergentes et lentilles divergentes et précisons leur nom.
$$\begin{array}{|c|c|c|}\hline\text{Lentilles}&\text{Nom}&\text{Type de lentille}\\ \hline L_{1}&\text{lentille biconvexe}&\text{convergente}\\ \hline L_{2}&\text{lentille plan-concave}&\text{divergente}\\ \hline L_{3}&\text{lentille ménisque}&\text{convergente}\\ \hline L_{4}&\text{lentille plan-convexe}&\text{convergente}\\ \hline L_{5}&\text{lentille ménisque}&\text{divergente}\\ \hline L_{6}&\text{lentille biconcave}&\text{divergente}\\ \hline\end{array}$$
4.2) Justification : on identifie ou on classe les lentilles selon leurs bords :
Ainsi, une lentille à bords minces est dite convergente et une lentille à bords épais est dite divergente.
Exercice 10 : Caractéristiques d'une lentille
L'axe optique principal d'une lentille convergente est dirigé vers le soleil.
Choisissons la bonne réponse :
1) L'axe optique principal d'une lentille est :
a) La droite perpendiculaire à cette lentille passant par son centre optique
2) Les rayons solaires convergent vers :
b) Le foyer objet de la lentille
3) La distance focale de la lentille est :
b) La distance entre le centre optique et le foyer image
4) La vergence d'une lentille est :
b) L'inverse de la distance focale
5) Dans le système international d'unités la vergence s'exprime en :
b) dioptrie
Exercice 11 Construire la marche d'un rayon lumineux
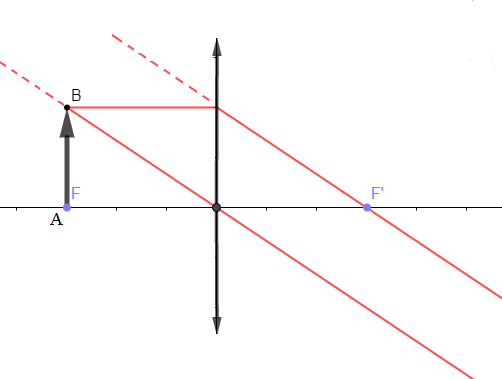
1) Chacun des schémas ci-dessous présente un rayon lumineux incident arrivant sur une lentille.
Construisons le rayon émergent correspondant (couleur verte).

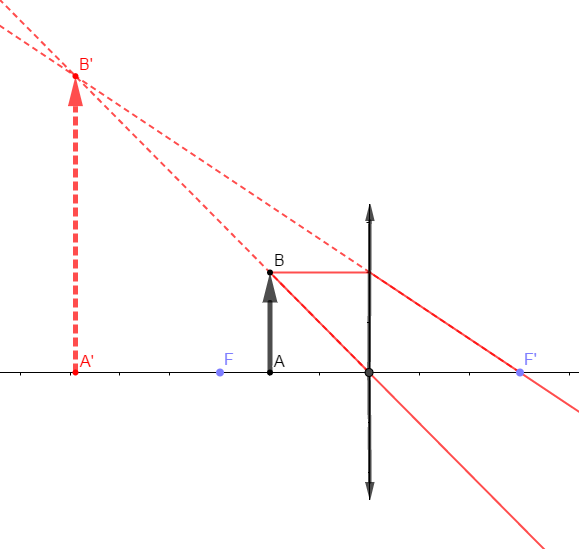
2) Chacun des schémas ci-dessous présente un rayon lumineux émergent après traversée d'une lentille.
Construisons le rayon incident correspondant (couleur rouge).

Exercice 12 Construction de l'image d'un objet réel donnée par une lentille convergente
Un objet lumineux $AB$ de hauteur $2\;cm$ est placé perpendiculairement à l'axe optique principal d'une lentille convergente de centre optique $O$ et de distance focale $3\;cm.$
Le point $A$ est sur l'axe optique principal, à $6\;cm$ de $O$
1) Calculons la vergence de la lentille
Soit $C$ la vergence de cette lentille alors, on a : $$C=\dfrac{1}{f}$$
où $f$ est la distance focale
A.N : $C=\dfrac{1}{3\;10^{-2}}=33.3$
D'où, $\boxed{C=33.3\;\delta}$
2) Construisons l'image $A'B'$ de $AB$

3) Donnons les caractéristiques de l'image $A'B'$
$-\ $ image réelle
$-\ $ image renversée
$-\ $ la taille de l'image est égale à celle de l'objet
$-\ $ image symétrique à l'objet par rapport au centre optique.
4) Déterminons le grandissement $G$ de l'image
Le grandissement $G$ de l'image est donné par : $$G=\dfrac{A'B'}{AB}$$
Comme l'image et l'objet ont la même taille alors, $\ AB=A'B'$
D'où, $$G=1$$
5) Reprenons les mêmes questions pour les cas suivants :
a) L'objet est placé à $7\;cm$ du centre optique
$\centerdot\ \ $ Vergence de la lentille
$$C=\dfrac{1}{f}$$
où $f$ est la distance focale
Ainsi, $C=\dfrac{1}{3\;10^{-2}}=33.3\;\delta$
$\centerdot\ \ $ Construction de l'image $A'B'$ de $AB$

$\centerdot\ \ $ Caractéristiques de l'image $A'B'$ :
$-\ $ image réelle
$-\ $ image renversée
$-\ $ image plus petite que l'objet
$-\ $ image sur le côté opposé telle que $OA'=5.1\;cm$
$\centerdot\ \ $ Grandissement $G$ de l'image
On a : $G=\dfrac{A'B'}{AB}\ $ or, $\dfrac{A'B'}{AB}=\dfrac{OA'}{OA}$
Donc, $G=\dfrac{OA'}{OA}=\dfrac{5.1}{7}=0.7$
D'où, $$G=0.7$$
b) L'objet est placé à $5\;cm$ du centre optique
$\centerdot\ \ $ Vergence de la lentille
$$C=\dfrac{1}{f}$$
où $f$ est la distance focale
Donc, $C=\dfrac{1}{3\;10^{-2}}=33.3\;\delta$
$\centerdot\ \ $ Construction de l'image $A'B'$ de $AB$

$\centerdot\ \ $ Caractéristiques de l'image $A'B'$ :
$-\ $ image réelle
$-\ $ image renversée
$-\ $ image plus grande que l'objet
$-\ $ image sur le côté opposé telle que $OA'=7.2\;cm$
$\centerdot\ \ $ Grandissement $G$ de l'image
On a : $G=\dfrac{A'B'}{AB}\ $ or, $\dfrac{A'B'}{AB}=\dfrac{OA'}{OA}$
Donc, $G=\dfrac{OA'}{OA}=\dfrac{7.2}{5}=1.4$
D'où, $$G=1.4$$
c) L'objet est placé sur le foyer objet
$\centerdot\ \ $ Vergence de la lentille
$$C=\dfrac{1}{f}$$
où $f$ est la distance focale
Ainsi, $C=\dfrac{1}{3\;10^{-2}}=33.3\;\delta$
L'objet étant placé sur le foyer $F$ alors, son image $A'B'$ est infinie.

d) L'objet est placé à $2\;cm$ du centre optique
$\centerdot\ \ $ Vergence de la lentille
$$C=\dfrac{1}{f}$$
où $f$ est la distance focale
Donc, $C=\dfrac{1}{3\;10^{-2}}=33.3\;\delta$
$\centerdot\ \ $ Construction de l'image $A'B'$ de $AB$

$\centerdot\ \ $ Caractéristiques de l'image $A'B'$ :
$-\ $ image virtuelle (non observable)
$-\ $ image droite (non renversée)
$-\ $ image plus grande que l'objet
$-\ $ image du même côté que l'objet telle que $OA'=5.9\;cm$
$\centerdot\ \ $ Grandissement $G$ de l'image
On a : $G=\dfrac{A'B'}{AB}=\dfrac{OA'}{OA}$
D'où, $G=\dfrac{5.9}{2}=2.9$
Exercice 13 Construction de l'image d'un objet réel situé en avant du foyer image d'une lentille divergente
Un objet lumineux $AB$ de hauteur $2\;cm$ est placé perpendiculairement à l'axe optique principal d'une lentille divergente de centre optique $O$ et de distance focale $3\;cm.$
Le point $A$ est sur l'axe principal, à $5\;cm$ de $O.$
1) Calculons la vergence de la lentille
Soit $C$ la vergence de la lentille. On a :
$$C=\dfrac{1}{f}$$
La lentille étant divergente donc, $f<0$
Ainsi, $f=-3\;cm=-3.10^{-2}\;m$
A.N : $C=\dfrac{1}{-3.10^{-2}}=-333.33$
D'où, $\boxed{C=-33.3\;\delta}$
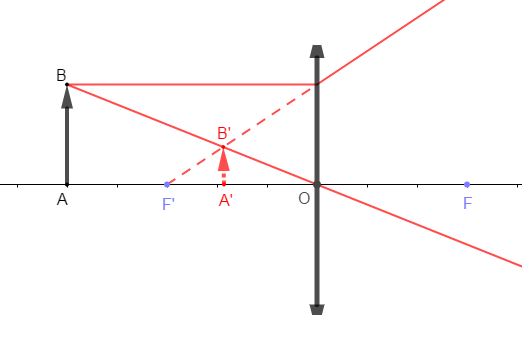
2) Construisons l'image $A'B'$ de $AB$

3) Donnons les caractéristiques de l'image $A'B'$
$-\ $ image virtuelle (non observable)
$-\ $ image droite (non renversée)
$-\ $ image plus petite que l'objet
$-\ $ image du même côté que l'objet telle que $OA'=1.8\;cm$
4) Définissons et déterminons le grandissement $G$ de l'image.
Le grandissement est une grandeur qui permet de déterminer la taille de l'image par rapport à l'objet.
$-\ $ Si $G<1$ alors, l'image est plus petite que l'objet.
$-\ $ Si $G>1$ alors, l'image est plus grande que l'objet.
$-\ $ Si $G=1$ alors, l'image est de même taille que l'objet.
On a :
$$G=\dfrac{A'B'}{AB}=\dfrac{OA'}{OA}$$
A.N : $G=\dfrac{1.8}{5}=0.36$
Donc, $\boxed{G=0.36}$
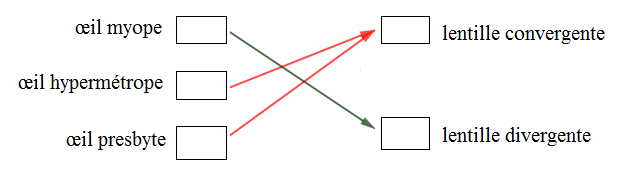
Exercice 14 Correction des anomalies de la vision
Recopions puis relions par une flèche le défaut de l'œil à la lentille qui permet sa correction.


Commentaires
Khoudia tall (non vérifié)
ven, 12/16/2022 - 19:03
Permalien
Thanks
Abissatou Bodian (non vérifié)
dim, 04/02/2023 - 00:48
Permalien
Réussir mon BFEM et avoir ma moyenne de classe
Anna Diallo (non vérifié)
jeu, 11/09/2023 - 22:21
Permalien
Réussir et bien comprendre mes leçons
Ndong (non vérifié)
jeu, 11/16/2023 - 16:50
Permalien
Je veux tout les exercices de
Ngoné sow (non vérifié)
jeu, 11/16/2023 - 21:22
Permalien
pc
ABDOURAHMAN (non vérifié)
dim, 12/31/2023 - 14:32
Permalien
j ai faussé que l exercice 11
Malang dabo (non vérifié)
mer, 08/21/2024 - 22:41
Permalien
La synthèse
sokhna oumy (non vérifié)
lun, 07/07/2025 - 20:27
Permalien
merci ....
Pages
Ajouter un commentaire