Vous êtes ici

Corrigé Bac Maths S2 1er groupe 2007

Exercice 1 (04 points)

On considère dans

$\mathbb{C}\;$ , l'équation :

$z^{3}-(3+2\mathrm{i})z^{2}+(1+4\mathrm{i})z+1-2\mathrm{i}=0$

1) a) Déterminons la solution réelle de cette équation.

Soit

$z=a$ la solution réelle de l'équation alors, on a :

$\begin{array}{rcl} a^{3}-(3+2\mathrm{i})a^{2}+(1+4\mathrm{i})a+1-2\mathrm{i}=0&\Rightarrow&a^{3}-3a^{2}-2\mathrm{i}a^{2}+a+4\mathrm{i}a+1-2\mathrm{i}=0\\\\&\Rightarrow&a^{3}-3a^{2}+a+1-(2a^{2}-4a+2)\mathrm{i}=0\end{array}$

Or, un nombre complexe est nul si, et seulement si, sa partie réelle et sa partie imaginaire sont toutes nulles.

Donc,

$\begin{array}{rcl} a^{3}-3a^{2}+a+1-(2a^{2}-4a+2)\mathrm{i}=0&\Leftrightarrow&\left\lbrace\begin{array}{rcl} a^{3}-3a^{2}+a+1&=&0 \\ 2a^{2}-4a+2&=&0\end{array}\right.\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl} a^{3}-3a^{2}+a+1&=&0 \\ 2(a^{2}-2a+1)&=&0\end{array}\right.\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl} a^{3}-3a^{2}+a+1&=&0 \\ (a-1)^{2}&=&0\end{array}\right.\\ \\ &\Leftrightarrow&\left\lbrace\begin{array}{rcl} a^{3}-3a^{2}+a+1&=&0 \quad(1) \\ a&=&1\quad(2)\end{array}\right.\end{array}$

$a=1$ vérifie aussi l'équation

$(1).$

Par conséquent,

$1$ est la solution réelle cherchée.

b) Montrons que

$\mathrm{i}$ est une solution de cette équation.

$\mathrm{i}$ est une solution de cette équation si, et seulement si,

$\mathrm{i}$ vérifie l'équation

Dans l'équation, en remplaçant

$z$ par

$\mathrm{i}$ , on obtient :

$\begin{array}{rcl}\mathrm{i}^{3}-(3+2\mathrm{i})\mathrm{i}^{2}+(1+4\mathrm{i})\mathrm{i}+1-2\mathrm{i}&=&-\mathrm{i}+3+2\mathrm{i}+\mathrm{i}-4+1-2\mathrm{i}\\\\&=&-3\mathrm{i}+3\mathrm{i}+6-6\\\\&=&0\end{array}$

Ce qui montre que

$\mathrm{i}$ est une solution de l'équation :

$z^{3}-(3+2\mathrm{i})z^{2}+(1+4\mathrm{i})z+1-2\mathrm{i}=0$

c) Déterminons la troisième solution de cette équation.

On a :

$z_{1}=1\$ et

$\ z_{2}=\mathrm{i}$ solutions de l'équation.

Soit

$z_{3}$ la troisième solution de cette équation.

Alors, l'équation peut encore s'écrire de la forme :

$(z-z_{1})(z-z_{2})(z-z_{3})$

En développant, on obtient :

$\begin{array}{rcl} (z-z_{1})(z-z_{2})(z-z_{3})&=&z^{3}-z_{1}z^{2}-z_{2}z^{2}-z_{3}z^{2}+z_{1}z_{2}z+z_{1}z_{3}z+z_{2}z_{3}z-z_{1}z_{2}z_{3}\\\\&=&z^{3}-(z_{1}+z_{2}+z_{3})z^{2}+(z_{1}z_{2}+z_{1}z_{3}+z_{2}z_{3})z-z_{1}z_{2}z_{3}\end{array}$

Par suite,

$z^{3}-(3+2\mathrm{i})z^{2}+(1+4\mathrm{i})z+1-2\mathrm{i}=z^{3}-(z_{1}+z_{2}+z_{3})z^{2}+(z_{1}z_{2}+z_{1}z_{3}+z_{2}z_{3})z-z_{1}z_{2}z_{3}$

Ainsi,

$\begin{array}{rcl}\left\lbrace\begin{array}{rcl} (z_{1}+z_{2}+z_{3})&=&(3+2\mathrm{i})\\ (z_{1}z_{2}+z_{1}z_{3}+z_{2}z_{3})&=&(1+4\mathrm{i})\\-z_{1}z_{2}z_{3}&=&1-2\mathrm{i}\end{array}\right.&\Leftrightarrow&\left\lbrace\begin{array}{rcl} 1+\mathrm{i}+z_{3}&=&3+2\mathrm{i}\\ \mathrm{i}+z_{3}+\mathrm{i}z_{3}&=&1+4\mathrm{i}\\-\mathrm{i}z_{3}&=&1-2\mathrm{i}\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} z_{3}&=&2+\mathrm{i}\\ \mathrm{i}+z_{3}+\mathrm{i}z_{3}&=&1+4\mathrm{i}\\-\mathrm{i}z_{3}&=&1-2\mathrm{i}\end{array}\right.\end{array}$

D'où,

$z_{3}=2+\mathrm{i}$ est la troisième solution de l'équation.

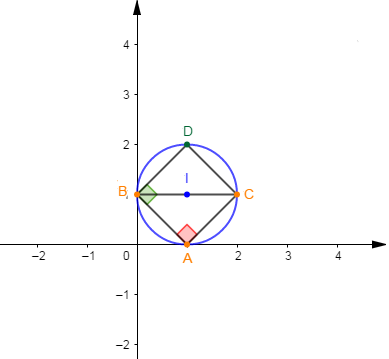
2) Soient les points

$A\;,\ B\$ et

$\ C$ d'affixes respectives

$1\;,\ \mathrm{i}\$ et

$\ 2+\mathrm{i}.$

a) Déterminons le module et un argument de

$\dfrac{z_{C}-z_{A}}{z_{B}-z_{A}}.$

On a :

$\begin{array}{rcl} \left|\dfrac{z_{C}-z_{A}}{z_{B}-z_{A}}\right|&=&\dfrac{|2+\mathrm{i}-1|}{|\mathrm{i}-1|}\\\\&=&\dfrac{|1+\mathrm{i}|}{|\mathrm{i}-1|}\\\\&=&\dfrac{\sqrt{2}}{\sqrt{2}}\\\\&=&1\end{array}$

Donc,

$\boxed{\left|\dfrac{z_{C}-z_{A}}{z_{B}-z_{A}}\right|=1}$

Soit :

$\begin{array}{rcl} arg\left(\dfrac{z_{C}-z_{A}}{z_{B}-z_{A}}\right)&=&arg\left(\dfrac{2+\mathrm{i}-1}{\mathrm{i}-1}\right)\\\\&=&arg(2+\mathrm{i}-1)-arg(\mathrm{i}-1)\\\\&=&arg(1+\mathrm{i})-arg(-1+\mathrm{i})\end{array}$

Or,

$1+\mathrm{i}=\sqrt{2}\left(\dfrac{\sqrt{2}}{2}+\mathrm{i}\dfrac{\sqrt{2}}{2}\right)=\sqrt{2}.\mathrm{e}^{\mathrm{i}\tfrac{\pi}{4}}$

$-1+\mathrm{i}=\sqrt{2}\left(-\dfrac{\sqrt{2}}{2}+\mathrm{i}\dfrac{\sqrt{2}}{2}\right)=\sqrt{2}.\mathrm{e}^{\mathrm{i}\tfrac{3\pi}{4}}$

Donc,

$arg(1+\mathrm{i})=\dfrac{\pi}{4}\$ et

$\ arg(-1+\mathrm{i})=\dfrac{3\pi}{4}$

Par suite,

$\begin{array}{rcl} arg(1+\mathrm{i})-arg(-1+\mathrm{i})&=&\dfrac{\pi}{4}-\dfrac{3\pi}{4}\\\\&=&\dfrac{-2\pi}{4}\\\\&=&-\dfrac{\pi}{2}\end{array}$

D'où,

$\boxed{arg\left(\dfrac{z_{C}-z_{A}}{z_{B}-z_{A}}\right)=-\dfrac{\pi}{2}\;[2\pi]}$

b) En déduisons la nature du triangle

$ABC.$

On sait que :

$\left|\dfrac{z_{C}-z_{A}}{z_{B}-z_{A}}\right|=\dfrac{||\overrightarrow{AC}||}{||\overrightarrow{AB}||}\$ et

$\ arg\left(\dfrac{z_{C}-z_{A}}{z_{B}-z_{A}}\right)=(\overrightarrow{AB}\;,\ \overrightarrow{AC})\;[2\pi]$

Or,

$\left|\dfrac{z_{C}-z_{A}}{z_{B}-z_{A}}\right|=1$ donc,

$||\overrightarrow{AC}||=||\overrightarrow{AB}||$

D'où,

$AB=AC$

Aussi,

$arg\left(\dfrac{z_{C}-z_{A}}{z_{B}-z_{A}}\right)=-\dfrac{\pi}{2}\;[2\pi]$ donc,

$(\overrightarrow{AB}\;,\ \overrightarrow{AC})=-\dfrac{\pi}{2}\;[2\pi]$

Par conséquent, le triangle

$ABC$ est rectangle isocèle en

$A.$

c) Déterminons l'affixe du point

$D$ image de

$A$ par la rotation de centre

$B$ et d'angle

$\dfrac{\pi}{2}.$

Considérons l'expression complexe de la rotation d'angle

$\dfrac{\pi}{2}$ , de centre

$B$ d'affixe

$\mathrm{i}$ qui, à tout point

$M$ d'affixe

$z$ associe le point

$M'$ d'affixe

$z'.$

Soit alors :

$z'-\mathrm{i}=\mathrm{e}^{\mathrm{i}\tfrac{\pi}{2}}(z-\mathrm{i})$

Donc, si

$D$ est image de

$A$ par cette rotation alors, son affixe

$z_{D}$ sera donné par :

$\begin{array}{rcl} z_{D}-\mathrm{i}=\mathrm{e}^{\mathrm{i}\tfrac{\pi}{2}}(z_{A}-\mathrm{i})&\Rightarrow&z_{D}=\mathrm{e}^{\mathrm{i}\tfrac{\pi}{2}}(1-\mathrm{i})+\mathrm{i}\\\\&\Rightarrow&z_{D}=\mathrm{i}(1-\mathrm{i})+\mathrm{i}\\\\&\Rightarrow&z_{D}=\mathrm{i}+1+\mathrm{i}\\\\&\Rightarrow&z_{D}=2\mathrm{i}+1\end{array}$

Ainsi,

$D$ est d'affixe

$2\mathrm{i}+1$

d) Montrons que

$A\;,\ B\;,\ C\$ et

$\ D$ sont sur un cercle de centre

$I(1+\mathrm{i})$ et de rayon

$r$ à déterminer.

On a :

$A\;,\ B\;,\ C\$ et

$\ D$ cocycliques ou appartiennent à un même cercle si, et seulement si,

$\dfrac{(z_{D}-z_{B})(z_{A}-z_{C})}{(z_{A}-z_{D})(z_{B}-z_{C})}\quad \text{est réel}$

Soit alors :

$\begin{array}{rcl}\dfrac{(z_{D}-z_{B})(z_{A}-z_{C})}{(z_{A}-z_{D})(z_{B}-z_{C})}&=&\dfrac{(2\mathrm{i}+1-\mathrm{i})(1-(2+\mathrm{i}))}{(1-(2\mathrm{i}+1))(\mathrm{i}-(2+\mathrm{i}))}\\\\&=&\dfrac{(\mathrm{i}+1)(-1-\mathrm{i})}{(-2\mathrm{i})(-2)}\\\\&=&\dfrac{-(\mathrm{i}+1)^{2}}{4\mathrm{i}}\\\\&=&\dfrac{-(-1+2\mathrm{i}+1)}{4\mathrm{i}}\\\\&=&\dfrac{(-2\mathrm{i})}{4\mathrm{i}}\\\\&=&-\dfrac{1}{2}\end{array}$

Ainsi,

$\boxed{\dfrac{(z_{D}-z_{B})(z_{A}-z_{C})}{(z_{A}-z_{D})(z_{B}-z_{C})}=-\dfrac{1}{2}\in\mathbb{R}}$

Ce qui prouve que les points

$A\;,\ B\;,\ C\$ et

$\ D$ sont sur un même cercle de centre

$I(1+\mathrm{i})$

En effet,

$ABC$ est rectangle isocèle en

$A$ donc, le centre

$I$ du cercle circonscrit à ce triangle est le milieu de l'hypoténuse

$[BC].$

Ainsi, son affixe sera donné par :

$\begin{array}{rcl} z_{I}&=&\dfrac{z_{B}+z_{C}}{2}\\\\&=&\dfrac{\mathrm{i}+2+\mathrm{i}}{2}\\\\&=&\dfrac{2\mathrm{i}+2}{2}\\\\&=&\mathrm{i}+1\end{array}$

D'où,

$\boxed{I(1+\mathrm{i})}$

Déterminons le rayon

$r$ de ce cercle.

Soit :

$\begin{array}{rcl} r&=&||\overrightarrow{IA}||\\\\&=&|z_{\overrightarrow{IA}}|\\\\&=&|1-(1+\mathrm{i})|\\\\&=&|1-1-\mathrm{i}|\\\\&=&|-\mathrm{i}|\\\\&=&1\end{array}$

Donc,

$\boxed{r=1}$

Exercice 2 (04 points)

1) On considère un dé cubique truqué dont les faces sont numérotées de

$1\$ à

$\ 6.$

On note

$p_{i}$ la probabilité d'apparition de la face numérotée

$i.$ Les

$p_{i}$ vérifient :

$p_{1}=p_{2}\;;\quad p_{3}=p_{4}=2p_{1}\;;\quad p_{5}=p_{6}=3p_{1}$

a) Montrons que

$p_{1}=\dfrac{1}{12}.$

On sait que :

$\sum_{i=1}^{6}p_{i}=1$

Alors,

$p_{1}+p_{2}+p_{3}+p_{4}+p_{5}+p_{6}=1$

Or,

$p_{2}=p_{1}\;;\quad p_{3}=p_{4}=2p_{1}\;;\quad p_{5}=p_{6}=3p_{1}$

Donc, en remplaçant, on obtient :

$\begin{array}{rcl} p_{1}+p_{2}+p_{3}+p_{4}+p_{5}+p_{6}=1&\Rightarrow&p_{1}+p_{1}+2p_{1}+2p_{1}+3p_{1}+3p_{1}=1\\\\&\Rightarrow&12p_{1}=1\\\\&\Rightarrow&p_{1}=\dfrac{1}{12}\end{array}$

D'où,

$\boxed{p_{1}=\dfrac{1}{12}}$

b) Montrons que la probabilité de l'événement

$A$ : "obtenir

$3$ ou

$6$ " est égale à

$\dfrac{5}{12}.$

Soit

$\{X=i\}$ l'événement "obtenir le numéro

$i$ " avec

$p(\{X=i\})=p_{i}$

Donc,

$A=\{X=3\}\cup\{X=6\}$ avec

$\{X=3\}\$ et

$\ \{X=6\}$ deux événements incompatibles.

Par suite,

$\begin{array}{rcl} p(A)&=&p(\{X=3\}\cup\{X=6\})\\\\&=&p(\{X=3\})+p(\{X=6\})-p\underbrace{(\{X=3\}\cap\{X=6\})}_{=0}\\\\&=&p_{3}+p_{6}\quad\text{or, }\quad p_{3}=2p_{1}\ \text{ et }p_{6}=3p_{1}\\\\&=&5p_{1}\\\\&=&5\times\dfrac{1}{12}\\\\&=&\dfrac{5}{12}\end{array}$

D'où,

$\boxed{p(A)=\dfrac{5}{12}}$

2) Un jeu d'adresse consiste à lancer le dé décrit ci-dessus puis à lancer une fléchette sur une cible fixe.

Si le joueur obtient

$3$ ou

$6$ , il se place à

$5\;m$ de la cible et lance la fléchette sur la cible ; à

$5\;m\;$ , la probabilité d'atteindre la cible est alors

$\dfrac{3}{5}.$

Si l'événement

$A$ n'est pas réalisé, il se place à

$7\;m$ de la cible et lance la fléchette ; à

$7\;m\;$ , la cible est atteinte avec une probabilité égale à

$\dfrac{2}{5}.$

On note

$C$ l'événement : "la cible est atteinte".

a) Déterminons

$p(C/A)\$ et

$\ p(C/\bar{A}).$

$p(C/A)$ est la probabilité d'atteindre la cible sachant que le joueur est à

$5\;m.$

Ainsi,

$\boxed{p(C/A)=\dfrac{3}{5}}$

$p(C/\bar{A})$ est la probabilité d'atteindre la cible sachant que le joueur est à

$7\;m.$

D'où,

$\boxed{p(C/\bar{A})=\dfrac{2}{5}}$

En déduisons que

$p(C)=\dfrac{29}{60}.$

D'après la formule des probabilités totales, on a :

$\begin{array}{rcl} p(C)&=&p(C/A)p(A)+p(C/\bar{A})p(\bar{A})\quad\text{or, }p(\bar{A})=1-p(A)\\\\&=&\dfrac{3}{5}\times\dfrac{5}{12}+\dfrac{2}{5}\times\left(1-\dfrac{5}{12}\right)\\\\&=&\dfrac{15}{60}+\dfrac{14}{60}\\\\&=&\dfrac{29}{60}\end{array}$

Ainsi,

$\boxed{p(C)=\dfrac{29}{60}}$

b) Déterminons

$p(A/C).$

Soit :

$p(A/C)=\dfrac{p(A\cap C)}{p(C)}$

Or,

$p(A\cap C)=p(C/A)\times p(A)$ donc, en remplaçant, on obtient :

$\begin{array}{rcl} p(A/C)&=&\dfrac{p(A\cap C)}{p(C)}\\\\&=&\dfrac{p(C/A)\times p(A)}{p(C)}\\\\&=&\dfrac{\dfrac{3}{5}\times\dfrac{5}{12}}{\dfrac{29}{60}}\\\\&=&\dfrac{15}{60}\times\dfrac{60}{29}\\\\&=&\dfrac{15}{29}\end{array}$

Donc,

$\boxed{p(A/C)=\dfrac{15}{29}}$

3) Le joueur dispose de

$10$ fléchettes qu'il doit lancer une à une, de façon indépendante, dans les mêmes conditions que précédemment définies.

Calculons la probabilité pour qu'il atteigne la cible exactement

$4$ fois.

En effet, nous sommes en présence d'un schéma de Bernoulli avec deux issues possibles : succès

$(S)$ lorsque la cible est atteinte et échec

$(E)$ lorsqu'elle ne l'est pas.

On a :

$p(S)=p(C)\$ et

$\ p(E)=1-p(S)=1-p(C)$

Soit

$Y$ la variable aléatoire de Bernoulli telle que :

$\{Y=k\}$ est l'événement "obtenir

$k$ succès sur

$n$ épreuves.

Alors, on a :

$p(\{Y=k\})=C_{n}^{k}.(p(S))^{k}.(p(E))^{n-k}$

Donc, la probabilité d'atteindre la cible exactement

$4$ fois (

$4$ succès et

$6$ échecs) lors des

$10$ lancées sera donnée par :

$\begin{array}{rcl} p(\{Y=4\})&=&C_{10}^{4}.(p(S))^{4}.(p(E))^{6}\\\\&=&C_{10}^{4}\times(p(C))^{4}\times (1-p(C))^{6}\\\\&=&C_{10}^{4}\times\left(\dfrac{29}{60}\right)^{4}\times\left(1-\dfrac{29}{60}\right)^{6}\\\\&=&210\times\left(\dfrac{29}{60}\right)^{4}\times\left(\dfrac{31}{60}\right)^{6}\\\\&=&0.22\end{array}$

D'où,

$\boxed{p(\{Y=4\})=0.22}$

Problème : (12 points)

Soit

$g$ la fonction définie sur

$]0\;;\ +\infty[$ par :

$g(x)=1+x+\ln x$

1) Dressons le tableau de variation de

$g.$

Soit

$g'$ la fonction dérivée de

$g$ alors, on a :

$g'(x)=1+\dfrac{1}{x}$

Donc,

$\forall\;x\in\;]0\;;\ +\infty[\;;\ g'(x)>0$

Par suite,

$g$ est strictement croissante sur

$]0\;;\ +\infty[.$

Par ailleurs,

$\begin{array}{rcl}\lim\limits_{x\rightarrow 0^{+}}g(x)&=&\lim\limits_{x\rightarrow 0^{+}}(1+x+\ln x)\\\\&=&-\infty\end{array}$

$\begin{array}{rcl}\lim\limits_{x\rightarrow +\infty}g(x)&=&\lim\limits_{x\rightarrow +\infty}(1+x+\ln x)\\\\&=&+\infty\end{array}$

D'où, le tableau de variations de

$g$ suivant :

$\begin{array}{|c|lcr|}\hline x&0&&+\infty\\ \hline g'(x)&|&+&\\ \hline&|&&+\infty\\g&|&\nearrow&\\&|-\infty&&\\ \hline \end{array}$

2) Montrons qu'il existe un unique réel

$\alpha$ solution de l'équation

$g(x)=0.$

En effet,

$g$ est continue et strictement croissante sur

$]0\;;\ +\infty[$ donc,

$g$ est une bijection de

$]0\;;\ +\infty[$ sur

$]-\infty\;;\ +\infty[$

Or,

$0\in\;]-\infty\;;\ +\infty[$ donc, d'après le théorème de la bijection, il existe un unique réel

$\alpha\in\;]0\;;\ +\infty[$ tel que

$g(\alpha)=0.$

Vérifions que

$\alpha$ appartient à

$]0.2\;;\ 0.3[.$

Soit :

$g(0.2)=1+0.2+\ln 0.2=-0.40\$ et

$\ g(0.3)=1+0.3+\ln 0.3=0.09$

Alors,

$g(0.2)\times g(0.3)=-0.036<0$

Ainsi,

$g$ est continue sur

$]0.2\;;\ 0.3[\$ et

$\ g(0.2)\times g(0.3)<0.$

Donc, d'après le corollaire du théorème des valeurs intermédiaires il existe

$\beta\in\;]0.2\;;\ 0.3[$ solution de l'équation

$g(x)=0.$

Or, l'unique solution de cette équation est le réel

$\alpha.$

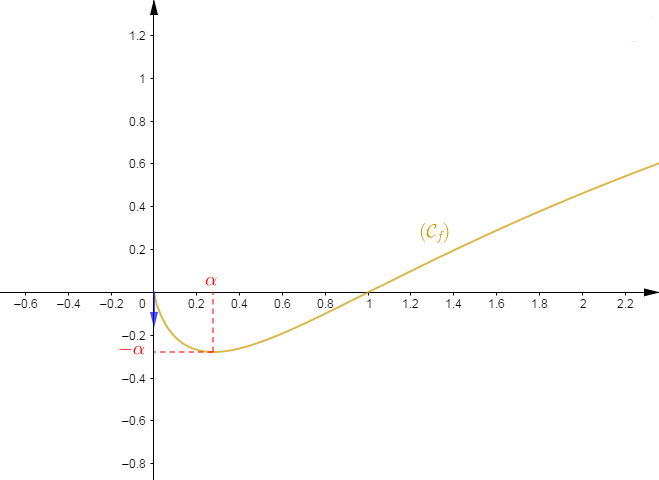
Par conséquent,

$\alpha=\beta.$ D'où,

$\alpha$ appartient à

$]0.2\;;\ 0.3[.$

3) En déduisons le signe de

$g$ sur

$]0\;;\ +\infty[.$

D'après les questions précédentes, on peut alors écrire :

$g(]0\;;\ \alpha])=]-\infty\;;\ 0]\quad\text{ et }\quad g([\alpha\;;\ +\infty[)=[0\;;\ +\infty[$

Ainsi,

$\centerdot\ \ g(x)\leq 0$ sur

$]0\;;\ \alpha]$

$\centerdot\ \ g(x)\geq 0$ sur

$[\alpha\;;\ +\infty[$

4) Établissons la relation

$\ln(\alpha)=-1-\alpha.$

D'après la question 2),

$\alpha$ est l'unique solution de l'équation

$g(x)=0.$

Ce qui signifie que

$g(\alpha)=0$

Par suite,

$\begin{array}{rcl} g(\alpha)=0&\Leftrightarrow&1+\alpha+\ln\alpha=0\\\\&\Leftrightarrow&\ln\alpha=-1-\alpha\end{array}$

D'où, la relation :

$\boxed{\ln(\alpha)=-1-\alpha}$

II.

On considère la fonction

$f$ définie par :

$f(x)=\left\{\begin{array}{ccl} \dfrac{x\ln x}{1+x}&\text{si }& x>0 \\ \\ 0&\text{si }& x=0 \end{array}\right.$

1) Montrons que

$f$ est continue en

$0$ puis sur

$]0\;;\ +\infty[.$

Calculons

$\lim\limits_{x\rightarrow 0^{+}}f(x)$

On a :

$\begin{array}{rcl}\lim\limits_{x\rightarrow 0^{+}}f(x)&=&\lim\limits_{x\rightarrow 0^{+}}\dfrac{x\ln x}{1+x}\\\\&=&\lim\limits_{x\rightarrow 0^{+}}\dfrac{0}{1}\\\\&=&0\end{array}$

Donc,

$\lim\limits_{x\rightarrow 0^{+}}f(x)=f(0).$

D'où,

$f$ est continue en

$0.$

Par ailleurs,

$\forall\;x_{0}\in\;]0\;;\ +\infty[\;;\ f$ est continue en

$x_{0}.$

Par conséquent,

$f$ est continue sur

$]0\;;\ +\infty[$

2) Étudions la dérivabilité de

$f$ en

$0.$

Calculons

$\lim\limits_{x\rightarrow 0^{+}}\dfrac{f(x)-f(0)}{x-0}$

On a :

$\begin{array}{rcl}\lim\limits_{x\rightarrow 0^{+}}\dfrac{f(x)-f(0)}{x-0}&=&\lim\limits_{x\rightarrow 0^{+}}\dfrac{\dfrac{x\ln x}{1+x}}{x}\\ \\&=&\lim\limits_{x\rightarrow 0^{+}}\dfrac{x\ln x}{x(1+x)}\\ \\&=&\lim\limits_{x\rightarrow 0^{+}}\dfrac{\ln x}{1+x}\\ \\&=&\lim\limits_{x\rightarrow 0^{+}}\dfrac{-\infty}{1}\\ \\&=&-\infty\end{array}$

Donc,

$\boxed{\lim\limits_{x\rightarrow 0^{+}}\dfrac{f(x)-f(0)}{x-0}=-\infty}$

Ainsi, la fonction

$f$ n'est pas dérivable en

$0.$

Interprétons graphiquement ce résultat.

Comme

$\lim\limits_{x\rightarrow 0^{+}}\dfrac{f(x)-f(0)}{x-0}=-\infty$ alors, la courbe représentative de

$f$ admet une demi-tangente verticale au point d'abscisse

$0.$

3) Déterminons la limite de

$f$ en

$+\infty.$

On a :

$\begin{array}{rcl}\lim\limits_{x\rightarrow +\infty}f(x)&=&\lim\limits_{x\rightarrow +\infty}\dfrac{x\ln x}{1+x}\\ \\&=&\lim\limits_{x\rightarrow +\infty}\dfrac{x}{x}\times\dfrac{\ln x}{\dfrac{1+x}{x}}\\ \\&=&\lim\limits_{x\rightarrow +\infty}\dfrac{\ln x}{\dfrac{1}{x}+1}\\ \\&=&\lim\limits_{x\rightarrow +\infty}\dfrac{+\infty}{0+1}\\ \\&=&+\infty\end{array}$

4) Montrons que, quel que soit

$x$ élément de

$]0\;;\ +\infty[$

$f'(x)=\dfrac{g(x)}{(1+x)^{2}}$

On a :

$\forall\;x\in\;]0\;;\ +\infty[\;;\ f(x)=\dfrac{x\ln x}{1+x}$

Par suite,

$\begin{array}{rcl} f'(x)&=&\dfrac{(1+\ln x)(1+x)-x\ln x}{(1+x)^{2}}\\\\&=&\dfrac{1+x+\ln x+x\ln x-x\ln x}{(1+x)^{2}}\\\\&=&\dfrac{1+x+\ln x}{(1+x)^{2}}\\\\&=&\dfrac{g(x)}{(1+x)^{2}}\end{array}$

Ainsi,

$\boxed{f'(x)=\dfrac{g(x)}{(1+x)^{2}}}$

En déduisons le signe de

$f'(x)$ sur

$]0\;;\ +\infty[.$

Comme

$(1+x)^{2}>0$ alors, le signe de

$f'(x)$ dépend uniquement du signe de

$g(x).$

Or,

$g(x)$ est négatif sur

$]0\;;\ \alpha]$ et positif sur

$[\alpha\;;\ +\infty[$

Par conséquent,

$\centerdot\ \ f'(x)\leq 0$ sur

$]0\;;\ \alpha]$

$\centerdot\ \ f'(x)\geq 0$ sur

$[\alpha\;;\ +\infty[$

5) Montrons que

$f(\alpha)=-\alpha.$

Soit :

$f(\alpha)=\dfrac{\alpha\ln\alpha}{1+\alpha}$

Or, dans la première partie, à la question 4), on avait :

$\ln\alpha=-1-\alpha.$

Donc, en remplaçant

$\ln\alpha$ par son expression, on obtient :

$\begin{array}{rcl} f(\alpha)&=&\dfrac{\alpha\ln\alpha}{1+\alpha}\\\\&=&\dfrac{\alpha(-1-\alpha)}{1+\alpha}\\\\&=&\dfrac{-\alpha(1+\alpha)}{1+\alpha}\\\\&=&-\alpha\end{array}$

Ainsi,

$\boxed{f(\alpha)=-\alpha}$

6) Dressons le tableau de variations de la fonction

$f.$

$\begin{array}{|c|lcccr|}\hline x&0&&\alpha&&+\infty\\ \hline f'(x)&|&-&0&+&\\ \hline&0&&&&+\infty\\f&&\searrow&&\nearrow&\\&&&-\alpha&&\\ \hline \end{array}$

7) Représentons la courbe de

$f$ dans le plan muni du repère orthonormal

$(O\;;\ \vec{i}\;,\ \vec{j}).$ Unité graphique :

$5\;cm\;.$ Prendre

$\alpha\approx 0.3.$

III.

1) A l'aide d'une intégration par parties, calculons l'intégrale

$I=\int_{1}^{\mathrm{e}}x\ln(x) \mathrm{d}x$

Posons :

$u'=x\$ et

$\ v=\ln x$ alors, on a :

$\begin{eqnarray} I&=&\int_{1}^{\mathrm{e}}x\ln(x) \mathrm{d}x\nonumber\\ \nonumber\\&=&\left[\dfrac{x^{2}\ln(x)}{2}\right]_{1}^{\mathrm{e}}-\int_{1}^{\mathrm{e}}\dfrac{x^{2}}{2x} \mathrm{d}x\nonumber\\ \nonumber\\&=&\dfrac{\mathrm{e}^{2}}{2}-\int_{1}^{\mathrm{e}}\dfrac{x}{2} \mathrm{d}x\nonumber\\ \nonumber\\&=&\dfrac{\mathrm{e}^{2}}{2}-\left[\dfrac{x^{2}}{4}\right]_{1}^{\mathrm{e}}\nonumber\\ \nonumber\\&=&\dfrac{\mathrm{e}^{2}}{2}-\left(\dfrac{\mathrm{e}^{2}}{4}-\dfrac{1}{4}\right)\nonumber\\ \nonumber\\&=&\dfrac{2\mathrm{e}^{2}}{4}-\dfrac{\mathrm{e}^{2}}{4}+\dfrac{1}{4}\nonumber\\ \nonumber\\&=&\dfrac{\mathrm{e}^{2}+1}{4}\nonumber \end{eqnarray}$

D'où,

$\boxed{I=\dfrac{\mathrm{e}^{2}+1}{4}}$

2) Montrons que pour tout

$x$ élément de

$[1\;;\ \mathrm{e}]$

$\dfrac{x\ln x}{\mathrm{e}+1}\leq f(x)\leq\dfrac{x\ln x}{2}$

Soit

$x\in[1\;;\ \mathrm{e}]$ alors, cela se traduit, sous forme d'intervalle par :

$1\leq x\leq\mathrm{e}$

Par suite,

$\begin{array}{rcl} 1\leq x\leq\mathrm{e}&\Rightarrow&1+1\leq 1+x\leq\mathrm{e}+1\\\\&\Rightarrow&\dfrac{1}{\mathrm{e}+1}\leq\dfrac{1}{1+x}\leq\dfrac{1}{2}\\\\&\Rightarrow&\dfrac{x\ln x}{\mathrm{e}+1}\leq\dfrac{x\ln x}{1+x}\leq\dfrac{x\ln x}{2}\end{array}$

D'où,

$\boxed{\forall\;x\in[1\;;\ \mathrm{e}]\;;\ \dfrac{x\ln x}{\mathrm{e}+1}\leq f(x)\leq\dfrac{x\ln x}{2}}$

En déduisons que :

$\dfrac{\mathrm{e}^{2}+1}{4(\mathrm{e}+1)}\leq\int_{1}^{\mathrm{e}}f(x)\mathrm{d}x\leq\dfrac{\mathrm{e}^{2}+1}{8}$

Comme

$\dfrac{x\ln x}{\mathrm{e}+1}\leq f(x)\leq\dfrac{x\ln x}{2}$ alors, par conservation de l'ordre de l'intégration, on obtient :

$\begin{eqnarray}\dfrac{x\ln x}{\mathrm{e}+1}\leq f(x)\leq\dfrac{x\ln x}{2}&\Rightarrow&\int_{1}^{\mathrm{e}}\dfrac{x\ln x}{\mathrm{e}+1}\mathrm{d}x\leq\int_{1}^{\mathrm{e}}f(x)\mathrm{d}x\leq\int_{1}^{\mathrm{e}}\dfrac{x\ln x}{2}\mathrm{d}x\nonumber\\ \nonumber\\ &\Rightarrow&\dfrac{1}{\mathrm{e}+1}\int_{1}^{\mathrm{e}}x\ln(x)\;\mathrm{d}x\leq\int_{1}^{\mathrm{e}}f(x)\mathrm{d}x\leq\dfrac{1}{2}\int_{1}^{\mathrm{e}}x\ln(x)\;\mathrm{d}x\nonumber\\ \nonumber\\ &\Rightarrow&\dfrac{1}{\mathrm{e}+1}\times\dfrac{\mathrm{e}^{2}+1}{4}\leq\int_{1}^{\mathrm{e}}f(x)\mathrm{d}x\leq\dfrac{1}{2}\times\dfrac{\mathrm{e}^{2}+1}{4}\nonumber\\ \nonumber\\ &\Rightarrow&\dfrac{\mathrm{e}^{2}+1}{4(\mathrm{e}+1)}\leq\int_{1}^{\mathrm{e}}f(x)\mathrm{d}x\leq\dfrac{\mathrm{e}^{2}+1}{8}\nonumber \end{eqnarray}$

D'où,

$\boxed{\dfrac{\mathrm{e}^{2}+1}{4(\mathrm{e}+1)}\leq\int_{1}^{\mathrm{e}}f(x)\mathrm{d}x\leq\dfrac{\mathrm{e}^{2}+1}{8}}$

Auteur:

Diny Faye