Solutions des exercices : Les hydrocarbures 3e
Classe:
Troisième
Exercice 1
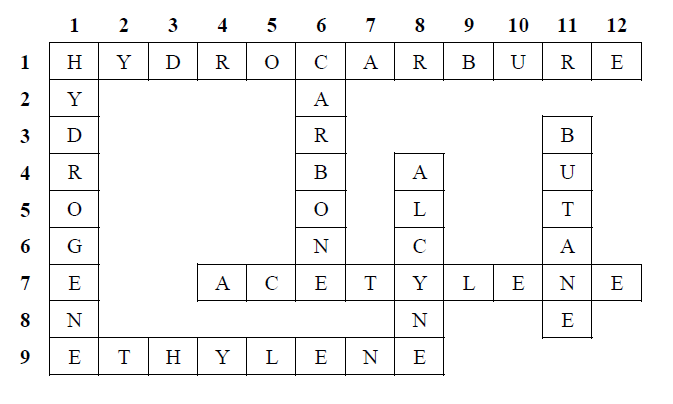
Exercice 2
1) $C_{n}H_{2n+1}\ +\ \left(\dfrac{6n+1}{4}\right)O_{2}\longrightarrow\ nCO_{2}\ +\ \left(\dfrac{2n+1}{2}\right)H_{2}O$
2) $C_{n}H_{2n}\ +\ \left(\dfrac{3n}{2}\right)O_{2}\longrightarrow\ nCO_{2}\ +\ nH_{2}O$
3) $C_{n}H_{2n-2}\ +\ \left(\dfrac{3n-1}{2}\right)O_{2}\longrightarrow\ nCO_{2}\ +\ (n-1)H_{2}O$
Exercice 3
Un hydrocarbure est un composé chimique constitué uniquement de carbone et d'hydrogène.
En analysant chaque composé :
- C₂H₄ (éthylène) : Oui Hydrocarbure (C et H seulement)
- C₂H₆O (alcool) : Non Pas un hydrocarbure (contient O)
- C₂H₂ (acétylène) : Oui Hydrocarbure (C et H seulement)
- C₆H₆ (benzène) : Oui Hydrocarbure (C et H seulement)
- CS₂ (sulfure de carbone) : Non Pas un hydrocarbure (contient S)
- C₅H₁₂ (pentane) : Oui Hydrocarbure (C et H seulement)
- H₂S (sulfure d'hydrogène) : Non Pas un hydrocarbure (ne contient pas de C)
Les hydrocarbures sont : C₂H₄, C₂H₂, C₆H₆ et C₅H₁₂
Exercice 4
Donnons la formule chimique :
1) d'un alcane dont la molécule renferme 6 atomes de carbone.
Soit $C_{n}H_{2n+2}$ un alcane avec 6 atomes de carbone donc, $n=6.$
Par suite, $2n+2=2\times 6+2=14$
D'où, la formule chimique est : $C_{6}H_{14}$
2) d'un alcène dont la molécule renferme 8 atomes d'hydrogène.
La formule générale d'un alcène est $C_{n}H_{2n}$, or la molécule renferme $8$ atomes d'hydrogène donc $2n=8\ \Rightarrow\ n=\dfrac{8}{2}=4$
D'où, la formule chimique de cet alcène est : $C_{4}H_{8}$
3) d'un alcyne dont la molécule renferme $5$ atomes de carbone.
La formule générale d'un alcyne est $C_{n}H_{2n-2}$ or, la molécule renferme 5 atomes de carbone donc $n=5\ \Rightarrow\ 2n-2=2\times 5-2=8$
D'où, la formule chimique de cet alcyne est : $C_{5}H_{8}$
Exercice 5
1) Trouvons la formule chimique de cet hydrocarbure
Soit $C_{x}H_{8}$ dont $M=80\;g/mol$
On a :
$\begin{array}{rcl} M_{C_{x}H_{8}}=12\times x+8\times 1=80&\Rightarrow&12x=80-8=72\\ \\&\Rightarrow&x=\dfrac{72}{12}\\ \\&\Rightarrow&x=6\end{array}$
D'où, la formule chimique de cet hydrocarbure est : $C_{6}H_{8}$
2) Calculons le volume de dioxyde de carbone obtenu.
Soit l'équation bilan suivante :
$$C_{6}H_{8}\ +\ 8O_{2}\ \longrightarrow\ 6CO_{2}\ +\ 4H_{2}O$$
On a :
$\begin{array}{rcl} \dfrac{n_{C_{6}H_{8}}}{1}=\dfrac{n_{CO_{2}}}{6}&\Rightarrow&6n_{C_{6}H_{8}}=n_{CO_{2}}\times 1\ \text{ or }\ n_{C_{6}H_{8}}=\dfrac{m_{C_{6}H_{8}}}{M_{C_{6}H_{8}}} \\ \\&\Rightarrow&6\times\dfrac{m_{C_{6}H_{8}}}{M_{C_{6}H_{8}}}=n_{CO_{2}}\ \text{ or }\ n_{CO_{2}}=\dfrac{V_{CO_{2}}}{V_{M_{CO_{2}}}}\ (CNTP)\\ \\&\Rightarrow&6\times\dfrac{m_{C_{6}H_{8}}}{M_{C_{6}H_{8}}}=\dfrac{V_{CO_{2}}}{V_{M_{CO_{2}}}}\\ \\&\Rightarrow&V_{CO_{2}}=\dfrac{6\times V_{M_{CO_{2}}}\times m_{C_{6}H_{8}}}{M_{C_{6}H_{8}}}\end{array}$
A.N : $V_{CO_{2}}=\dfrac{6\times 22.4\times 20.5}{82}=33.6$
Donc, $\boxed{V_{CO_{2}}=33.6\;l}$
3) Donnons la formule chimique d'un alcane dont la masse molaire est $72\;g/mol.$
La formule générale d'un alcane est $C_{2n}H_{2n+2}$
On a :
$\begin{array}{rcl} M_{C_{n}H_{2n+2}}=12n+2n+2=72\;g/mol&\Rightarrow&14n+2=72\\ \\&\Rightarrow&14n=70\\ \\&\Rightarrow&n=\dfrac{70}{14}=5\end{array}$
D'où, la formule chimique de cet hydrocarbure est : $C_{5}H_{12}$
Exercice 6
Soit l'équation bilan suivante :
$$C_{n}H_{2n+2}\ +\ \left(\dfrac{3n+1}{2}\right)O_{2}\ \longrightarrow\ nCO_{2}\ +\ (n+1)H_{2}O$$
Trouvons la formule brute
On a :
$\begin{array}{rcl} \dfrac{n_{C_{n}H_{2n+2}}}{1}=\dfrac{n_{CO_{2}}}{n}&\Rightarrow&n\times n_{C_{n}H_{2n+2}}=n_{CO_{2}}\times 1\ \text{ or }\ n_{gaz}=\dfrac{V_{gaz}}{V_{M_{gaz}}}\\ \\&\Rightarrow&\dfrac{nV_{C_{n}H_{2n+2}}}{V_{M_{C_{2}H_{2n+2}}}}=\dfrac{V_{CO_{2}}}{V_{M_{CO_{2}}}} \\ \\&\Rightarrow&nV_{C_{n}H_{2n+2}}=V_{CO_{2}}\\ \\&\Rightarrow&n=\dfrac{V_{C_{n}H_{2n+2}}}{V_{CO_{2}}}\end{array}$
A.N : $n=\dfrac{68}{17}=4$
D'où, la formule brute de cet alcane est : $C_{4}H_{10}$
Exercice 7
1) Écrivons l'équation bilan de la combustion complète du butane
$$C_{4}H_{10}\ +\ \dfrac{13}{2}O_{2}\ \longrightarrow\ 4CO_{2}\ +\ 5H_{2}O$$
2) Trouvons le volume de dioxygène, mesuré dans les conditions normales, nécessaire pour la combustion complète.
Soit l'équation bilan $C_{4}H_{10}\ +\ \dfrac{13}{2}O_{2}\ \longrightarrow\ 4CO_{2}\ +\ 5H_{2}O$ alors, dans les conditions stœchiométriques on a :
$\begin{array}{rcl}\dfrac{n_{C_{4}H_{10}}}{1}=\dfrac{n_{O_{2}}}{\dfrac{13}{2}}&\Rightarrow&13n_{C_{4}H_{10}}=2n_{O_{2}}\times 1\ \text{ or }\ n_{C_{4}H_{10}}=\dfrac{m_{C_{4}H_{10}}}{M_{C_{4}H_{10}}}\\ \\&\Rightarrow&13\times\dfrac{m_{C_{4}H_{10}}}{M_{C_{4}H_{10}}}=2n_{O_{2}}\ \text{ or }\ n_{O_{2}}=\dfrac{V_{O_{2}}}{V_{M_{O_{2}}}}\ (CNTP)\\ \\&\Rightarrow&13\times\dfrac{m_{C_{4}H_{10}}}{M_{C_{4}H_{10}}}=\dfrac{2V_{O_{2}}}{V_{M_{O_{2}}}} \\ \\&\Rightarrow&V_{O_{2}}=\dfrac{13\times V_{M_{O_{2}}}\times m_{C_{4}H_{10}}}{2\times M_{C_{4}H_{10}}}\end{array}$
avec $M_{C_{4}H_{10}}=58\;g/mol\ $ et $\ V_{M_{O_{2}}}=22.4\;mol/l$
A.N : $V_{O_{2}}=\dfrac{13\times 22.4\times 13\;10^{3}}{2\times 58}=32634.482$
Donc, $\boxed{V_{O_{2}}=32634.5\;l}$
Déduisons en le volume d'air nécessaire.
Dans la composition de l'air on a $21\%$ de $O_{2}$.
Donc, $\dfrac{V_{O_{2}}}{V_{air}}\times 100=21\ \Rightarrow\ V_{air}=\dfrac{V_{O_{2}}\times 100}{21}$
A.N : $V_{air}=\dfrac{32634.5\times 100}{21}=155402.4$
D'où, $\boxed{V_{air}=155402.4\;l}$
Exercice 8
On a $C_{12}H_{26}$
Posons :
$\begin{array}{rcl} n=12&\Rightarrow&2n=24\\&\Rightarrow&2n+2=26\end{array}$
Alors, cet hydrocarbure peut s'écrire sous la forme $C_{n}H_{2n+2}$ donc il appartient à la famille des alcanes.
Calculons masse minimale de dioxygène qu'il faut prévoir pour brûler les $600$ tonnes de kérosène.
Équation bilan de la réaction : $C_{12}H_{26}\ +\ \dfrac{37}{2}O_{2}\ \longrightarrow\ 12CO_{2}\ +\ 13H_{2}O$
Pour une combustion complète du kérosène, on a :
$\begin{array}{rcl} \dfrac{n_{C_{12}H_{26}}}{1}=\dfrac{n_{O_{2}}}{\dfrac{37}{2}}&\Rightarrow&37n_{C_{12}H_{26}}=2n_{O_{2}}\times 1\ \text{ or }\ n_{C_{12}H_{26}}=\dfrac{m_{C_{12}H_{26}}}{M_{C_{12}H_{26}}}\\ \\&\Rightarrow&37\times\dfrac{m_{C_{12}H_{26}}}{M_{C_{12}H_{26}}}=2\times\dfrac{m_{O_{2}}}{M_{O_{2}}}\\ \\&\Rightarrow&m_{O_{2}}=\dfrac{37\times M_{O_{2}}\times m_{C_{12}H_{26}}}{2\times M_{C_{12}H_{26}}}\end{array}$
avec $M_{C_{12}H_{26}}=12\times 12+26\times 1=170\;g/mol\ $ et $\ M_{O_{2}}=2\times 16\;mol/l$
A.N : $m_{O_{2}}=\dfrac{37\times 32\times 600\;10^{6}}{2\times 170}=2089411.765$
Donc, $\boxed{m_{O_{2}}=2.089\;tonnes}$
Exercice 9
1) Écrivons l'équation bilan de la combustion complète du composé $A$
$A$ est un hydrocarbure donc $A$ est de la forme $C_{x}H_{y}$
$$\left(x+\dfrac{y}{4}\right)O_{2}+C_{x}H_{y}\longrightarrow xCO_{2}+\dfrac{y}{2}H_{2}O$$
2) Déterminons le volume de $O_{2}$ réagi et de $CO_{2}$ formé.
Après refroidissement, on constate qu'il reste dans l'eudiomètre un mélange gazeux constitué de $40\;cm^{3}$ de dioxyde de carbone et $20\;cm^{3}$ de dioxygène.
Donc le volume de $O_{2}$ réagi est donné par $V_{O_{2}}=80\;cm^{3}-20\;cm^{3}=60\;cm^{3}$ et le volume de $CO_{2}$ formé reste égal à $40\;cm^{3}.$
3) Déterminons la formule brute du composé $A$
Soit $n$ le nombre de mols et $V$ le volume de gaz, alors $n=\dfrac{V}{V}_{m}$
Cherchons $x$
On a : $\ \dfrac{n(O_{2})}{x+\dfrac{y}{4}}=n(C_{x}H_{y})=\dfrac{n(CO_{2})}{x}$
Or, $\ n(C_{x}H_{y})=\dfrac{V_{C_{x}H_{y}}}{V_{m}}$
Donc, $\dfrac{n(CO_{2})}{x}=\dfrac{V_{C_{x}H_{y}}}{V_{m}}\ $ avec, $\ n(CO_{2})=\dfrac{V_{CO_{2}}}{V_{m}}$
Par suite,
$\begin{array}{rcl}\dfrac{V_{C_{x}H_{y}}}{V_{m}}=\dfrac{\dfrac{V_{CO_{2}}}{V_{m}}}{x}&\Rightarrow&\dfrac{V_{C_{x}H_{y}}}{V_{m}}=\dfrac{V_{CO_{2}}}{V_{m}\times x}\\ \\&\Rightarrow&V_{C_{x}H_{y}}=\dfrac{V_{CO_{2}}}{x}\\ \\&\Rightarrow&x=\dfrac{V_{Co_{2}}}{V_{C_{x}H_{y}}}\end{array}$
A.N : $x=\dfrac{40}{10}=4\ \Rightarrow\ \boxed{x=4}$
Cherchons $y$
On a :
$\begin{array}{rcl}\dfrac{n(O_{2})}{x+\dfrac{y}{4}}=\dfrac{n(CO_{2})}{x}&\Rightarrow&x\;n(O_{2})=\dfrac{4x+y}{4}\left[n(CO_{2})\right]\\ \\&\Rightarrow&\dfrac{x(V_{O_{2}})}{V_{m}}=\dfrac{4x+y}{4}\left(\dfrac{V_{CO_{2}}}{V_{m}}\right)\\ \\&\Rightarrow&\dfrac{x\;V_{O_{2}}}{V_{m}}=\dfrac{(4x+y)(V_{CO_{2}})}{4 V_{m}}\\ \\&\Rightarrow&60x=\dfrac{(4x+y)40}{4}\\ \\&\Rightarrow&240x=40(4x+y)\end{array}$
Or, $x=4$ donc $960=640+40y\ \Rightarrow\ y=\dfrac{960-640}{40}$
D'où, $\boxed{y=8}$
La formule brute de $A$ est donc : $\boxed{C_{4}H_{8}}$
Exercice 10
Complétons les phrases ci-dessous
1) Les hydrocarbures sont des composés ne contenant que les éléments carbone et hydrogène. Les alcanes ont pour formule générale $C_{n}H_{2n+2}.$
2) Les alcènes ont pour formule générale $C_{n}H_{2n}$
3) L'acétylène de formule $C_{2}H_{2}$ est un hydrocarbure appartenant à la famille des alcynes.
4) La combustion complète d'un hydrocarbure dans le dioxygène donne du dioxyde de carbone et de l'eau.
5) Si la combustion est incomplète, il se forme entre autres des fumées noires de carbone.
Exercice 11
1) Un hydrocarbure est un corps organique dont la molécule ne renferme que du carbone et de l'hydrogène.
2) Citons trois familles d'hydrocarbures et précisons leurs formules générales :
$-\ $ Les alcanes sont des hydrocarbures de formule générale $C_{n}H_{2n+2}.$
$-\ $ Les hydrocarbures dont la formule générale est $C_{n}H_{2n}$ sont appelés alcènes.
$-\ $ Parmi les familles d'hydrocarbures, il existe celle dont la formule générale est $C_{n}H_{2n-2}\ :$ c'est la famille des alcynes.
3) En précisant leurs familles, déterminons ceux qui sont des hydrocarbures parmi les corps suivants :
$\centerdot\ C_{3}H_{4}\ $ cette molécule est composée de trois atomes de carbone et quatre atomes d'hydrogène. Donc, c'est un hydrocarbure.
Soit : $n=3 \Rightarrow 2n=2\times 3=6$
Or, $4=6-2 \Rightarrow 4=2n-2$ donc, cette molécule appartient à la famille à la famille des hydrocarbures dont la formule générale est $C_{n}H_{2n-2}\ :$ c'est un alcyne
$\centerdot\ CO_{2}\ :$ dans cette molécule, il y a un atome de carbone et deux atomes d'oxygène : elle n'est pas un hydrocarbure.
$\centerdot\ NH_{3}\ :$ il y a un atome d'azote et trois atomes d'hydrogène dans cette molécule. elle n'est pas hydrocarbure.
$\centerdot\ H_{2}O\ :$ la molécule d'eau est composée de deux atomes d'hydrogène et un atome de d'oxygène : l'eau n'est pas un hydrocarbure.
$\centerdot\ C_{2}H_{2}\ :$ cette molécule est composée de deux atomes de carbone et deux atomes d'hydrogène : c'est un hydrocarbure.
Soit : $n=2 \Rightarrow 2n=4\ $ et $\ 2=4-2=2n-2.$
D'où, ce composé appartient à la famille des alcynes dont la formule générale est $C_{n}H_{2n-2}.$
$\centerdot\ O_{2}\ :$ Le dioxygène est une molécule diatomique. Donc il n'est pas hydrocarbure.
$\centerdot\ CH_{4}\ :$ il y a un atome de carbone et quatre atomes d'hydrogène dans cette molécule : c'est un hydrocarbure.
Soit : $n=1 \Rightarrow 2n=2\ $ et $\ 4=2+2.$
D'où la formule générale de cet hydrocarbure est $C_{n}H_{2n+2}\ :$ c'est un alcane.
Exercice 12
1) Identification d'un alcane
a) Déterminons l'expression de la masse molaire moléculaire d'un alcane possédant $n$ atomes de carbone :
Soit un alcane de formule général $C_{n}H_{2n+2}$ alors, sa masse molaire moléculaire est :
$\begin{array}{rcl} M(C_{n}H_{2n+2})&=&12\times n+1(2n+2)\\ \\&=&12n+2n+2\\ \\&=&14n+2\end{array}$
Donc, $\boxed{M(C_{n}H_{2n+2})=14n+2}$
b) En déduisons la formule brute d'un alcane dont la masse molaire est $M=30\,g\cdot mol^{-1}$
On a : $M(C_{n}H_{2n+2})=14n+2\ $ or, $M(C_{n}H_{2n+2})=30$ donc,
$\begin{array}{rcl} 14n+2=30&\Rightarrow&14n=30-2=28\\ \\&\Rightarrow&n=\dfrac{28}{14}\\ \\&\Rightarrow&n=2\end{array}$
Ainsi, $\boxed{n=2}$
D'où : la formule brute de cet alcane est :
$$\boxed{C_{2}H_{6}}$$
2) identification d'un alcène
a) Déterminons l'expression de sa masse molaire
Soit un alcène de formule général $C_{n}H_{2n}$ alors, sa masse molaire est donnée par :
$\begin{array}{rcl} M(C_{n}H_{2n})&=&12\times n+1\times 2n\\ \\&=&12n+2n\\ \\&=&14n\end{array}$
Donc, $\boxed{M(C_{n}H_{2n})=14n}$
b) En déduisons la formule brute d'un alcène dont la masse molaire est $28\,g\cdot mol^{-1}$
Soit : $M(C_{n}H_{2n})=14n.$ Comme $M=28$ alors, on a :
$\begin{array}{rcrcl} 14n=28&\Rightarrow&n&=&\dfrac{28}{14}\\ \\&\Rightarrow&n&=&2\end{array}$
Donc, $\boxed{n=2}$
D'où, la formule brute de cet alcène est :
$$\boxed{C_{2}H_{4}}$$
3) Identification d'un alcyne
a) Déterminons l'expression de la masse molaire d'un alcyne possédant $n$ atomes de carbone
On a :
$\begin{array}{rcl} M(C_{n}H_{2n-2})&=&12\times n+1(2n-2)\\ \\&=&12n+2n-2=14n-2\\ \\&=&14n-2\end{array}$
Donc, $\boxed{M(C_{n}H_{2n-2})=14n-2}$
b) En déduisons la formule brute d'un alcyne de masse molaire $M=26\,g\cdot mol^{-1}$
Soit $M(C_{n}H_{2n-2})=14n-2\ $ or, $M=26$ donc, on a :
$\begin{array}{rcl} 14n-2=26&\Rightarrow&14n=26+2=28\\ \\&\Rightarrow&n=\dfrac{28}{2}\\ \\&\Rightarrow&n=2\end{array}$
Donc, $\boxed{n=2}$
D'où, la formule brute est donnée par :
$$\boxed{C_{2}H_{2}}$$
4) La densité d'un alcane gazeux est $2$
a) Rappelons la formule de la densité d'un gaz par rapport à l'air :
$$\boxed{d=\dfrac{M}{29}}$$
b) Trouvons la formule brute de l'alcane :
On a :
$\begin{array}{rcl} d=\dfrac{M}{29}=2&\Rightarrow&M=29\times 2\\ \\&\Rightarrow&M=58=14n+2\\ \\&\Rightarrow&58-2=14n\\ \\&\Rightarrow&n=\dfrac{56}{14}\\ \\&\Rightarrow&n=4\end{array}$
Donc, $\boxed{n=4}$
Ainsi, la formule brute de l'alcane est donnée par :
$$\boxed{C_{4}H_{10}}$$
Exercice 13
Complétons et équilibrons les équations
$C_{3}H_{8}\ +\ 5O_{2}\ \longrightarrow\ 3CO_{2}\ +\ 4 H_{2}O$
$C_{2}H_{4}\ +\ 3O_{2}\ \longrightarrow\ 2CO_{2}\ +\ 2H_{2}O$
$C_{2}H_{2}\ +\ \dfrac{5}{2}O_{2}\ \longrightarrow\ H_{2}O\ +\ 2CO_{2}$
$C_{4}H_{10}\ +\ \dfrac{13}{2}O_{2}\ \longrightarrow\ 4CO_{2}\ +\ 5H_{2}O$
Exercice 14
Le méthane $CH_{4}$ brule dans le dioxygène $O_{2}$ en donnant du dioxyde de carbone $CO_{2}$ et de l'eau $H_{2}O.$
1) Écrivons l'équation bilan de la réaction
$$CH_{4}\ +\ 2O_{2}\ \longrightarrow\ CO_{2}\ +\ 2H_{2}O$$
2) Donnons l'interprétation du bilan en mole
Une mole de méthane réagit avec deux moles de dioxygène pour donner une mole de dioxyde de carbone et deux moles d'eau.
Ainsi,
$$\dfrac{n(CH_{4})}{1}=\dfrac{n(O_{2})}{2}=\dfrac{n(CO_{2})}{1}=\dfrac{n(H_{2}O)}{2}$$
3) On dispose de trois moles de méthane.
a) Déterminons la quantité de matière de dioxygène nécessaire pour que la combustion soit complète.
D'après la question 2), on a :
$\dfrac{n(CH_{4})}{1}=\dfrac{n(O_{2})}{2}\ \Rightarrow\ n(O_{2})=2n(CH_{4})$
A.N : $n(O_{2}=2\times 3=6$
D'où,
$$\boxed{n(O_{2})=6\,mol}$$
b) Calculons :
$-\ $ Le volume de dioxyde de carbone
On a : $n=\dfrac{V}{V_{M}}\ \Rightarrow\ V=n\times V_{M}\ $ avec, $V_{M}=24\,L\cdot mol^{-1}$
Détermination de $n(CO_{2})$
On a : $\dfrac{n(CH_{4})}{1}=\dfrac{n(CO_{2})}{1}\ \Rightarrow\ n(CO_{2})=n(CH_{4})=3\,mol$
A.N : $V(CO_{2})=3\times24$
Ainsi,
$$\boxed{V(CO_{2})=72\,L}$$
$-\ $ La masse d'eau formée
On a : $n=\dfrac{m}{M}\ \Rightarrow\ m=n\times M\ $ or,
$\begin{array}{rcl} M(H_{2}O)&=&2M(H)+M(O)\\ \\&=&2\times 1+16\\ \\&=&18\,g\cdot mol^{-1}\end{array}$
De plus, $n(H_{2}O)=2n(CH_{4})=2\times 3=6\,mol$, d'après le bilan molaire.
Donc, $m(H_{2}O)=6\times 18=108$
D'où,
$$\boxed{m(H_{2}O)=108\,g}$$

Commentaires
Rama (non vérifié)
mar, 09/24/2024 - 19:55
Permalien
Réuissir le BFM
Aminata ndoye (non vérifié)
dim, 11/06/2022 - 15:07
Permalien
C très cool
Toufa (non vérifié)
dim, 11/20/2022 - 18:34
Permalien
Devoir PC 3eme
ndeye seye (non vérifié)
ven, 12/09/2022 - 22:00
Permalien
pc
Anonyme (non vérifié)
mer, 05/31/2023 - 14:52
Permalien
Pdf
Anonyme (non vérifié)
sam, 06/10/2023 - 00:24
Permalien
C'est trop utile
Anonyme (non vérifié)
sam, 06/10/2023 - 00:24
Permalien
C'est trop utile
Anonyme (non vérifié)
ven, 10/20/2023 - 16:43
Permalien
Correction des exercices 15
A (non vérifié)
ven, 10/20/2023 - 17:53
Permalien
Erreur
Cheikh omar (non vérifié)
mer, 11/15/2023 - 22:04
Permalien
Ľ exo à été moins détaillé.
Anonyme
lun, 04/29/2024 - 00:33
Permalien
Bonsoir je voudrai la
Anonyme (non vérifié)
lun, 04/29/2024 - 00:48
Permalien
Correction de ľexercice16 et
Anonyme (non vérifié)
lun, 04/29/2024 - 00:49
Permalien
Correction de ľexercice 15 et
Anonyme (non vérifié)
jeu, 06/13/2024 - 20:57
Permalien
Très intéressant
Woury diallo (non vérifié)
lun, 11/04/2024 - 00:32
Permalien
C'est très sympa
Alimatou loum (non vérifié)
mer, 11/20/2024 - 17:38
Permalien
Les lentilles minces
Mouhamed mbaye (non vérifié)
ven, 11/22/2024 - 18:37
Permalien
Pc
Irissa (non vérifié)
lun, 03/17/2025 - 01:17
Permalien
Cahier
marie mendy (non vérifié)
mer, 12/17/2025 - 22:11
Permalien
repondre
Pages
Ajouter un commentaire