Vous êtes ici

Généralités sur les fonctions - 1er S

Classe:

Première

I Définition de fonctions et applications

I.1 Définition

$\centerdot\ \$ Soient

$E$ et

$F$ deux ensembles, on appelle fonction toute relation qui associe à tout élément de

$E$ au plus un élément de

$F.$

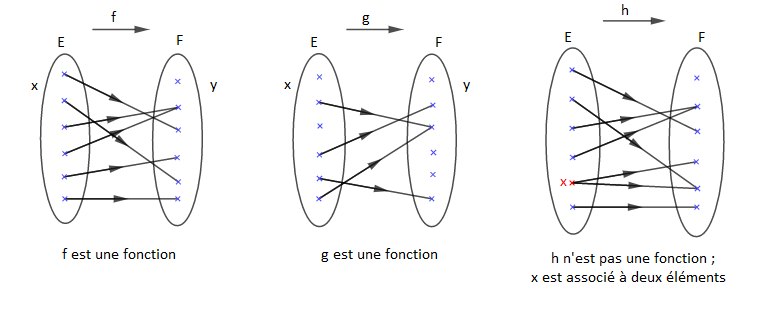
$\centerdot\ \$ On appelle fonction d'une variable réelle à valeurs réelles une application qui à tout élément

$x$ d'une partie

$D$ de

$\mathbb{R}$ associe un réel et un seul noté

$f(x)$

$-\$ Le réel

$y=f(x)$ est appelé image de

$x$ par

$f$

$-\$

$x$ est un antécédent de

$y$

$-\$ La partie

$D$ est appelée ensemble de définition de la fonction.

$\centerdot\ \$ Soit

$f$ une fonction définie sur

$D$ , et

$E\subset D$ , alors

$f(E)$ désigne l'ensemble des images des éléments de

$E$ .

Notation

$\begin{eqnarray} f\;:\;D & \longrightarrow & \mathbb{R} \nonumber \\x & \longmapsto & f(x) \nonumber\end{eqnarray}$

I.2 Ensemble de définition

Soit

$f$ une fonction d'une variable réelle

$x$ , on appelle ensemble de définition de

$f$ l'ensemble noté

$D_{f}=\{x\in\mathbb{R}\;/\;f(x)\; \text{ existe }\}$

Exemple 1 :

La fonction identité

$x\longmapsto x$ est définie sur

$D=\mathbb{R}$

La fonction élévation au carré

$x\longmapsto x^{2}$ est définie sur

$D=\mathbb{R}$

La fonction inverse

$x\longmapsto \frac{1}{x}$ est définie sur

$D=\mathbb{R^{*}}=\mathbb{R}\setminus\{0\}$

La fonction racine carré

$x\longmapsto \sqrt{x}$ est définie sur

$D=\mathbb{R_{+}}=[0; +\infty[$

Exemple 2 :

Déterminer l'ensemble de définition des fonctions suivantes.

$f(x)=x^{2}-5x$

$g(x)=\sqrt{x^{2}-4x+3}$

$h(x)=\dfrac{2x+1}{x^{2}-4}$

$k(x)=\left\{\begin{array}{lll}\dfrac{2x+1}{x^{2}-1}\quad &\text{si }& x<0 \\ \\ \dfrac{\sqrt{x^{2}-x}}{x-9}\quad &\text{si }& x\geq 0\end{array}\right.$

Solution

a) Nous savons que

$x^{2}-5x$ est un polynôme de degré deux, donc

$\forall\;x\in\mathbb{R}\;;\ x^{2}-5x\;$ existe.

Ainsi,

$D_{f}=\mathbb{R}$

b) On a

$g(x)$ existe si, et seulement si,

$x^{2}-4x+3\geq 0.$

Soit le trinôme du second degré suivant :

$x^{2}-4x+3$

On a

$\Delta=b^{2}-4ac=16-12=4$

$\Delta>0$ donc le trinôme admet deux racines distinctes

$x_{1}$ et

$x_{2}$ telles que

$x_{1}=\dfrac{4-2}{2}=1$ et

$x_{2}=\dfrac{4+2}{2}=3.$

Ainsi, le trinôme est du signe de

$a$ à l'extérieur des racines et du signe de

$-a$ à l'intérieur.

$a$ étant positif, donc

$x^{2}-4x+3\geq 0$ sur

$]-\infty\;;\ 1]\cup[3\;;\ +\infty[.$

D'où,

$D_{g}=]-\infty\;;\ 1]\cup[3\;;\ +\infty[$

c) On a :

$\begin{array}{rcl} h(x)\;\text{ existe } & \Leftrightarrow & x^{2}-4\neq 0 \\ \\ & \Leftrightarrow & (x-2)(x+2)\neq 0 \\ \\ & \Leftrightarrow & x\neq 2\;\text{ ou }\;x\neq -2\end{array}$

D'où,

$D_{h}=\mathbb{R}\setminus\{-2\;;\ 2\}$

d) Pour

$x<0\;,\ k_{1}(x)=\dfrac{2x+1}{x^{2}-1}$

on a :

$\begin{array}{rcl} k(x)\;\text{ existe } & \Leftrightarrow & x^{2}-1\neq 0 \\ \\ & \Leftrightarrow & (x-1)(x+1)\neq 0 \\ \\ & \Leftrightarrow & x\neq 1\;\text{ ou }\;x\neq -1 \end{array}$

donc,

$D_{k_{1}}=]-\infty\;;\ -1[\cup]-1\;;\ 0[$

pour

$x\geq 0\;,\ k_{2}(x)=\dfrac{\sqrt{x^{2}-x}}{x-9}$

on a

$\begin{array}{rcl} k(x)\;\text{ existe } & \Leftrightarrow & x^{2}-x\geq 0\;\text{ et }\;x-9\neq 0 \\ \\ & \Leftrightarrow & x(x-1)\geq 0\;\text{ et }\;x\neq 9 \\ \\ & \Leftrightarrow & x\geq 1\;\text{ et }\;x\neq 9 \end{array}$

donc,

$D_{k_{2}}=\{0\}\cup[1\;;\ 9[\cup]9\;;\ +\infty[$

D'où,

$D_{k}=D_{k_{1}}\cup D_{k_{2}}=]-\infty\;;\ 0]\cup[1\;;\ +\infty[\setminus\{-1\;;\ 9\}$

Remarque :

Il ne faut pas confondre

$f$ appelé fonction ; avec

$f(x)$ (désigné aussi par

$y$ ) qui est le réel associé par

$f$ à un élément donné

$x$ .

I.3 Courbe représentative d'une fonction

Soit

$f$ une fonction définie sur

$D_{f}$

La courbe représentative de

$f$ notée

$\mathcal{C}_{f}$ dans un repère est l'ensemble des points

$M(x, f(x))$ avec

$x\in D_{f}$

On dit que

$y=f(x)$ est une équation de cette courbe dans le repère considéré.

On note

$\left\{M\begin{pmatrix} x\\ y\end{pmatrix}\;\text{ tel que }x\in D_{f}\;\text{ et }y=f(x)\right\}$

I.4 Application

I.4.1 Définition

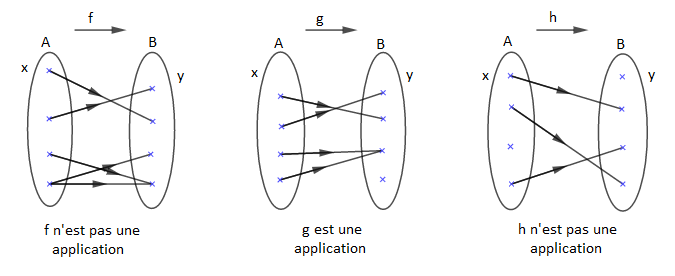
On appelle application de

$A$ vers

$B$ toute relation de

$A$ vers

$B$ qui associe tout élément de

$A$ , un et un seul élément de

$B.$

Remarque :

$\begin{eqnarray} f\;:\;I & \longrightarrow & \mathbb{R} \nonumber \\ x & \longmapsto & f(x) \nonumber \end{eqnarray}$

Pour que

$f$ soit une application il faudrait que

$I\subset D_{f}.$

Toute application est une fonction. La réciproque est fausse.

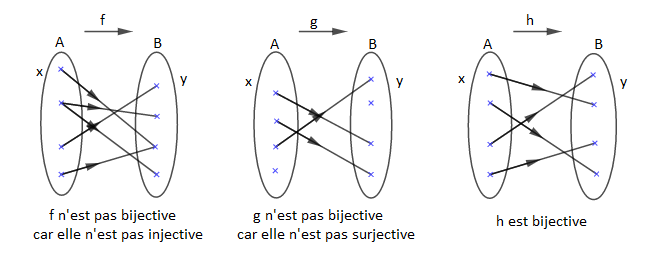
I.4.2 Applications injectives, surjectives, bijectives

a) Application injective ou injection

Une application

$f\;:\;E\longrightarrow F$ est dite injective si, et seulement si, deux éléments différents de l'ensemble de points

$E$ ont des images différentes dans

$F.$

Remarque :

Une application

$f\;:\;E\longrightarrow F$ n'est pas injective s'il y a deux éléments différents de

$E$ qui ont la même image dans

$F.$

b) Théorème de caractérisation de l'injection

Une application

$f\;:\;E\longrightarrow F$ est dite injective si, et seulement si,

$x\neq x'\;\Rightarrow\;f(x)\neq f(x')$

ou encore

$f$ est dite injection si, et seulement si,

$f(x)=f(x')\;\Rightarrow\; x=x'$

Exemple :

$\begin{eqnarray} f\;:\;[1\;;\ +\infty[ & \longrightarrow & \mathbb{R} \nonumber \\ x & \longmapsto & x^{2}\nonumber \end{eqnarray}$

Soient

$x$ et

$x'$ dans

$[1\;;\ +\infty[\;$ , alors

$\begin{array}{rcl} f(x)=f(x') & \Rightarrow & x^{2}=x'^{2} \\ \\ & \Rightarrow & x=x' \end{array}$

d'où

$f$ est injective

c) Application surjective ou surjection

Une application

$f\;:\;E\longrightarrow F$ est dite surjective si, et seulement si,

$\forall\;y\in F\;,\ \exists\;x\in E\;\text{ tel que }\;f(x)=y$

Exemple :

$\begin{eqnarray} f\;:\;\mathbb{R} & \longrightarrow & \mathbb{R} \nonumber \\ x & \longmapsto & x^{2} \nonumber \end{eqnarray}$

$f$ n'est pas surjective car si

$y<0$ , alors on aura

$x^{2}=y<0$ ; ce qui est impossible.

$\begin{eqnarray} g\;:\;[1\;;\ +\infty[ & \longrightarrow & \mathbb{R} \nonumber \\ x & \longmapsto & x^{2}-4 \nonumber \end{eqnarray}$

$\begin{array}{rcl} g(x)=y & \Leftrightarrow & x^{2}-4=y \\ \\ & \Leftrightarrow & y+4=x^{2}\quad\text{impossible si, }y<-4 \end{array}$

$\begin{array}{rcl} g(x)=-7 & \Leftrightarrow & x^{2}-4=-7 \\ \\ & \Leftrightarrow & x^{2}=-3\quad\text{impossible } \end{array}$

donc

$g$ n'est pas surjective

$\begin{eqnarray} h\;:\;\mathbb{R}\setminus\{2\} & \longrightarrow & \mathbb{R}\setminus\{1\} \nonumber \\ x & \longmapsto & \dfrac{x+1}{x-2}\nonumber \end{eqnarray}$

$\begin{array}{rcl} h(x)=y & \Leftrightarrow & \dfrac{x+1}{x-2}=y \\ \\ & \Leftrightarrow & x+1=yx-2y \\\\ & \Leftrightarrow & x-yx=-1-2y \\\\ & \Leftrightarrow & x(1-y)=-1-2y \\\\ & \Leftrightarrow & x=\dfrac{-1-2y}{1-y}=\dfrac{1+2y}{y-1}\;\text{ avec }y\neq 1 \end{array}$

donc

$h$ est surjective

d) Application bijective ou bijection

Soit

$f$ une application de

$A$ vers

$B$

$\begin{eqnarray} f\;:\;A & \longrightarrow & B \nonumber \\ x & \longmapsto & f(x)=y \nonumber \end{eqnarray}$

$f$ est dite bijective si

$f$ est à la fois injective et surjective.

e) Théorème de caractérisation

Une application

$f\;:\;A\longrightarrow B$ est bijective si, et seulement si,

$\forall\;y\in B\;,\ \text{ il existe un unique }\;x\in A\;\text{ tel que }\;f(x)=y$

$f$ est bijective, alors elle admet une bijection réciproque que l'on note

$f^{-1}$ qui va de

$B$ vers

$A.$

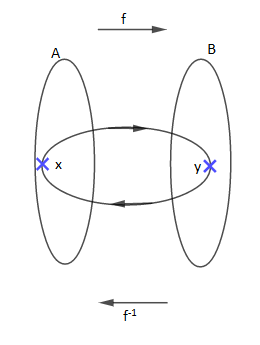
$f(x)=y\;\text{ si, et seulement si, }x=f^{-1}(y)$

II Opérations sur les fonctions

II.1 Égalité de deux fonctions

Soient

$f$ et

$g$ deux fonctions définies respectivement sur

$D_{f}$ et

$D_{g}$

On dit que les deux fonction

$f$ et

$g$ sont égales si, et seulement si,

$D_{f}=D_{g}\;\text{ et }\;\forall\;x\in D_{f}\;,\ f(x)=g(x)$

$f=g\;\Leftrightarrow \left\{\begin{array}{rrr} D_{f}&=&D_{g}\\ \forall\; x\in D_{f},\quad f(x)&=&g(x) \end{array}\right.$

II.2 Somme de deux fonctions

Soient

$f$ et

$g$ deux fonctions définies respectivement sur

$D_{f}$ et

$D_{g}$

On définit sur

$D=D_{f}\cap D_{g}$ la somme

$f+g$ par

$\forall\; x\in D\;,\ f+g:\:x\longmapsto f(x)+g(x)$

On peut aussi écrire

$\forall\; x\in D\;,\ (f+g)(x)=f(x)+g(x)$

Exemple :

soit

$f\;:\; x\longmapsto \dfrac{1}{x+2}$ et

$g\;:\; x\longmapsto \dfrac{1}{x-2}$ deux fonctions définies sur l'intervalle

$]-2\;;\ 2[$

La somme

$f+g\;:\; x\longmapsto \dfrac{1}{x+2}+\dfrac{1}{x-2}=\dfrac{x-2+x+2}{(x+2)(x-2)}=\dfrac{2x}{x^{2}-4}$ est définie sur

$]-2\;;\ 2[$

II.3 Produit d'une fonction par un réel

$f$ une fonction définie sur

$D$ et pour tout réel

$k$ , le produit d'un réel

$k$ par la fonction

$f$ est noté :

$kf$ et se définit par

$\forall\; k\in\mathbb{R}\;,\ \forall\; x\in D\;,\ kf\;:\;x\longmapsto kf(x)$

On peut aussi écrire le produit

$kf$ d'un réel

$k$ par une fonction

$f$

$\forall\; k\in\mathbb{R}\;,\ \forall\; x\in D\;,\ (kf)(x)=kf(x)$

II.4 Produit de deux fonctions

On définit sur

$D=D_{f}\cap D_{g}$ le produit

$fg$ par

$\forall\; x\in D\;,\ fg\;:\;x\longmapsto f(x)g(x)$

On peut aussi écrire

$\forall\; x\in D\;,\ (fg)(x)=f(x)g(x)$

Exemple :

soit

$f\;:\; x\longmapsto \dfrac{1}{x}$ et

$g\;:\; x\longmapsto \dfrac{1}{x-1}$ deux fonctions définies sur l'intervalle

$]0\;;\ 1[$

Le produit

$fg\;:\; x\longmapsto \dfrac{1}{x}.\dfrac{1}{x-1}=\dfrac{1}{x(x-1)}$ est définie sur

$]0\;;\ 1[$

Remarque :

Le produit

$fg$ peut donner une fonction nulle sans qu'aucune des deux fonctions

$f$ et

$g$ soit identiquement nulle.

Exemple :

$f\;:\;x\longmapsto\left\{\begin{array}{rrr} 0\quad \text{si}\quad x\in [0\;;\ 1]\\ x\quad \text{si}\quad x\in [1\;;\ 2] \end{array}\right.$ et

$g\;:\;x\longmapsto\left\{\begin{array}{rrr} x\quad \text{si}\quad x\in [0\;;\ 1]\\ 0\quad \text{si}\quad x\in [1\;;\ 2]\end{array}\right.$

Le produit

$fg \quad x\longmapsto 0$ si

$x\in [0\;;\ 2]$ est la fonction nulle sur

$[0\;;\ 2]$ bien que ni

$f$ ni

$g$ ne soit la fonction nulle.

II.5 Quotient de deux fonctions

On définit sur

$D=D_{f}\cap D_{g}$ , le quotient

$\dfrac{f}{g}$ tel que pour tout

$x$ de

$D$ tel que

$g(x)\neq 0$ par

$\dfrac{f}{g}\;:\;x\longmapsto\dfrac{f(x)}{g(x)}$

On peut aussi écrire

$\forall\;x\in D\;;\ g(x)\neq 0\;,\ \left(\dfrac{f}{g}\right)(x)=\dfrac{f(x)}{g(x)}$

Exemple :

soit

$f\;:\; x\longmapsto \dfrac{1}{x+1}$ et

$g\;:\; x\longmapsto \dfrac{1}{x-1}$ deux fonctions définies sur l'intervalle

$]-1\;;\ 1[$

Le quotient

$\dfrac{f}{g}\;:\; x\longmapsto \dfrac{\dfrac{1}{x+1}}{\dfrac{1}{x-1}}=\dfrac{x-1}{x+1}$ est définie sur

$]-1\;;\ 1[$

Remarque :

Le quotient

$\dfrac{f}{g}\;:\; x\longmapsto \dfrac{x-1}{x+1}$ est même définie sur

$]-1\;;\ 1]$

III Composition de deux fonctions

Soient

$f$ et

$g$ deux fonctions numériques de la variable

$x\in\mathbb{R}$ définies respectivement sur

$D_{f}$ et

$D_{g}.$

Soit

$D$ l'ensemble des éléments

$x$ de

$D_{f}$ tels que

$f(x)\in D_{g}.$

La composée

$g\circ f$ ("

$g$ rond

$f$ ") est la fonction numérique, d'ensemble de définition

$D$ , définie par

$(g\circ f)(x)=g[f(x)]$ (on remplace

$x$ par l'expression de

$f(x)$ dans

$g(x)).$

Dans l'écriture

$g\circ f$ la première application est

$f$ et la seconde est

$g.$

De même,

$(f\circ g)(x)=f[g(x)]$ (on remplace

$x$ par l'expression de

$g(x)$ dans

$f(x)).$

On a :

$(g\circ f)(x)=g[f(x)]\;\exists\;\Leftrightarrow\left\{\begin{array}{rrr} x\in D_{f}\\ f(x)\in D_{g} \end{array}\right.$

$(f\circ g)(x)=f[g(x)]\;\exists\;\Leftrightarrow\left\{\begin{array}{rrr} x\in D_{g}\\ g(x)\in D_{f} \end{array}\right.$

Exemple :

Soit

$f:\: x\longmapsto x^{2}-1$ et

$g:\: x\longmapsto \dfrac{1}{x}$

On a

$D_{f}=\mathbb{R}$ et

$D_{g}=\mathbb{R^{*}}=\mathbb{R}\setminus\{0\}$

Pour tout

$x\in D_{f}=\mathbb{R}$ tel que

$f(x)\neq 0$ c'est-à-dire pour

$x^{2}-1\neq 0$ ou encore pour

$x\in D=\mathbb{R}\setminus\{-1\;;\ 1\}$ , la composée

$g\circ f$ des deux applications

$f$ et

$g$ est

$(g\circ f)(x)=g[f(x)]=g[(x^{2}-1)]=\dfrac{1}{x^{2}-1}$

$\begin{eqnarray} g\circ f\;:\;\mathbb{R}\setminus\{-1\;;\ 1\} & \longrightarrow & \mathbb{R} \nonumber \\ x & \longmapsto & \dfrac{1}{x^{2}-1} \nonumber \end{eqnarray}$

Exemple :

Soit :

$\begin{eqnarray} f \;:\;]-1\;;\ 1] & \longrightarrow & \mathbb{R} \nonumber \\ x & \longmapsto & \dfrac{1-x}{1+x} \nonumber \end{eqnarray}$

Calculons

$f\circ f=f^{2}$

On a :

$\forall\;x\in\;]-1\;;\ 1]$

$\begin{array}{rcl} f^{2}(x)&=&(f\circ f)(x) \\ \\& = & f\left[\dfrac{1-x}{1+x}\right] \\ \\ & = & \dfrac{1-\dfrac{1-x}{1+x}}{1+\dfrac{1-x}{1+x}} \\ \\ & = & \dfrac{\dfrac{1+x-1+x}{1+x}}{\dfrac{1+x+1-x}{1+x}} \\ \\ & = & x \end{array}$

et donc,

$\begin{eqnarray} f^{2}\;:\;]-1\;;\ 1] & \longrightarrow & \mathbb{R} \nonumber \\ x & \longmapsto & x \nonumber \end{eqnarray}$

Propriété :

La composition des applications est associatives

$(h\circ g)\circ f=h\circ (g\circ f)$ mais attention! elle n'est pas commutative

$g\circ f\neq f\circ g$

Exemple :

Soit :

$\begin{eqnarray} f\;:\;\mathbb{R} & \longrightarrow & \mathbb{R} \nonumber \\ x & \longmapsto & 2x+3 \nonumber \end{eqnarray}$

$\begin{eqnarray} g\;:\;\mathbb{R} & \longrightarrow & \mathbb{R} \nonumber \\ x & \longmapsto & x^{2} \nonumber \end{eqnarray}$

alors,

$\forall\;x\in\mathbb{R}\;,\ (g\circ f)(x)=g[2x+3]=(2x+3)^{2}=4x^{2}+12x+9$

$\forall\;x\in\mathbb{R}\;,\ (f\circ g)(x)=f[x^{2}]=2x^{2}+3$

et donc,

$\begin{eqnarray} g\circ f\;:\;\mathbb{R} & \longrightarrow & \mathbb{R} \nonumber \\ x & \longmapsto & 4x^{2}+12x+9 \nonumber \end{eqnarray}$

$\begin{eqnarray} f\circ g\;:\;\mathbb{R} & \longrightarrow & \mathbb{R} \nonumber \\ x & \longmapsto & 2x^{2}+3 \nonumber \end{eqnarray}$

Par conséquent,

$g\circ f\neq f\circ g$ (même si les deux composée existent)

Attention !

Il ne faut pas confondre le produit de deux fonctions et la composition de ces deux fonctions.

Exemple :

Considérons les deux fonctions

$f\;:\; x\longmapsto x-1$ et

$g\;:\; x\longmapsto \dfrac{1}{x^{2}+1}$ , ces deux fonctions sont définies sur

$D=\mathbb{R}$

La fonction produit

$fg$ est la fonction

$fg\;:\; x\longmapsto \dfrac{x-1}{x^{2}+1}$

La fonction composée

$g\circ f$ est la fonction

$(g\circ f)(x)=g[f(x)]=g[(x-1)]=\dfrac{1}{(x-1)^{2}+1}$

Soit

$g\circ f\;:\; x\longmapsto \dfrac{1}{x^{2}-2x+2}$

IV Les formules de changement de repère (par translation)

Le plan est muni d'un repère

$(O;\ \vec{i},\ \vec{j})$ et

$\mathcal{C}_{f}$ est la courbe représentative de

$y=f(x)$ dans ce repère.

Soit

$\Omega$ le point de coordonnées

$(a, b)$ dans le repère

$(O;\ \vec{i},\ \vec{j})$ .

Alors,

$\overrightarrow{O\Omega}=a\vec{i}+b\vec{j}$

Quelle est l'équation de la courbe

$\mathcal{C}_{f}$ dans le nouveau repère

$(\Omega;\ \vec{i},\ \vec{j})\;?$

Désignons par

$(x,\ y)$ les (anciennes) coordonnées d'un point

$M$ du plan dans le repère

$(O;\ \vec{i},\ \vec{j})$

Vectoriellement, on peut écrire

$\overrightarrow{OM}=x\vec{i}+y\vec{j}$ et par

$(X,\ Y)$ les (nouvelles) coordonnées du même point

$M$ dans le repère

$(\Omega;\ \vec{i},\ \vec{j})$

De même, vectoriellement

$\overrightarrow{\Omega M}=X\vec{i}+Y\vec{j}$

La relation de Chasles

$\overrightarrow{OM}=\overrightarrow{O\Omega}+\overrightarrow{\Omega M}$ donne par passage aux coordonnées

$\left\{\begin{array}{lcr} x &=& X+a\\ y &=& Y+b\end{array}\right.$ ou encore

$\left\{\begin{array}{lcr} X &=& x-a\\ Y &=& y-b\end{array}\right.$

qui sont les formules de changement de repère (par translation)

V Restriction et prolongement d'une fonction

$\centerdot\ \$ Soit

$f$ une fonction numérique de la variable réelle

$x$ .

On dit que

$f_{1}$ est une restriction de

$f$ sur un intervalle

$I$ de

$\mathbb{R}$ si, et seulement si,

$I\subset D_{f}\;\text{ et }\;\forall\;x\in I\;,\ f_{1}(x)=f(x)$

la restriction de

$f$ sur peut être notée

$f/I$

Exemple :

$f(x)=\left|\dfrac{x^{2}-4}{x}\right|$

Soit

$f_{1}$ la restriction de

$f$ sur

$[-2\;;\ 0[$

On a

$f_{1}(x)=\dfrac{x^{2}-4}{x}$

$g(x)=\left\{\begin{array}{lll}\dfrac{x^{2}-4x}{x^{2}-1}\quad &\text{si }& x\leq 0 \\ \\ \sqrt{x^{2}+x}\quad &\text{si }& x>0\end{array}\right.$

Soient

$g_{1}$ et

$g_{2}$ les restrictions de

$g$ respectivement sur

$]0\;;\ +\infty[$ et sur

$]-\infty\;;\ -1[\cup]-1\;;\ 0]$

alors on a :

$g_{1}(x)=\sqrt{x^{2}+x}$ et

$g_{2}=\dfrac{x^{2}-4x}{x^{2}-1}$

$\centerdot\ \$ Soit

$f$ une fonction numérique de la variable réelle

$x$ définie sur

$I.$

On dit que

$f_{1}$ est un prolongement de

$f$ sur un intervalle

$J$ de

$\mathbb{R}$ si, et seulement si,

$I\subset J\;\text{ et }\;\forall\;x\in I\;,\ f(x)=f_{1}(x)$

Exemple :

$h(x)=x^{2}\sin\dfrac{1}{x}\;,\ D_{h}=\mathbb{R}\setminus\{0\}$

Soit

$h_{1}(x)=\left\{\begin{array}{lll} x^{2}\sin\dfrac{1}{x}\quad &\text{si }& x\neq 0 \\ \\ 0\quad &\text{si }& x=0 \end{array}\right.$

alors on a :

$I=\mathbb{R}\setminus\{0\}$ et

$J=\mathbb{R}$

ainsi,

$h_{1}$ est un prolongement de

$h$ sur

$\mathbb{R}$

VI Parité et éléments de symétrie

VI.1 Parité d'une fonction

$\centerdot\ \$ On dit qu'une fonction

$f$ est paire si, et seulement si, les deux conditions suivantes sont vérifiées

$C_{1}\;:\quad\text{ si }\;x\in D_{f}\;\text{ alors }-x\in D_{f}$

$C_{2}\;:\quad\forall\;x\in D_{f}\;;\ f(-x)=f(x)$

$\centerdot\ \$ On dit qu'une fonction

$f$ est impaire si, et seulement si, les deux conditions suivantes sont vérifiées

$C_{1}\;:\quad\text{ si }\;x\in D_{f}\;\text{ alors }-x\in D_{f}$

$C_{2}\;:\quad\forall\;x\in D_{f}\;;\ f(-x)=-f(x)$

Exemple :

Étudier la parité des fonctions suivantes :

$f(x)=x^{2}$

$g(x)=x\sqrt{x^{2}-1}$

$h(x)=\dfrac{2x}{x^{2}-4}$

$k(x)=\dfrac{x^{2}+1}{x-2}$

Solution

a) On a

$D_{f}=\mathbb{R}$

$C_{1}\;:\;x\in \mathbb{R}\;\text{ alors }-x\in \mathbb{R}$

$C_{2}\;:\forall\;x\in \mathbb{R}\;;\ f(-x)=(-x)^{2}=x^{2}=f(x)$

d'où

$f$ est paire

$D_{g}=]-\infty\;;\ -1]\cup[1\;;\ +\infty[$

$C_{1}\;:$

$\begin{array}{rcl} x\in D_{g} & \Rightarrow & x\leq -1\;\text{ ou }\;x\geq 1 \\ \\ & \Rightarrow & -x\geq 1\;\text{ ou }\;-x\leq -1 \\ \\ & \Rightarrow & -x\in D_{g} \end{array}$

$C_{2}\;:\forall\;x\in D_{g}\;;\ g(-x)=(-x)\sqrt{(-x)^{2}-1}=-x\sqrt{x^{2}-1}=-g(x)$

donc,

$g$ est impaire

$D_{h}=\mathbb{R}\setminus\{-2\;;\ 2\}$

$C_{1}\;:$

$\begin{array}{rcl} x\in D_{h} & \Rightarrow & x\neq -2\;\text{ et }\;x\neq 2 \\ \\ & \Rightarrow & -x\neq 2\;\text{ et }-x\neq -2 \\ \\ & \Rightarrow & -x\in D_{h} \end{array}$

$C_{2}\;:\forall\;x\in D_{h}\;;\ h(-x)=\dfrac{2(-x)}{(-x)^{2}-4}=\dfrac{-2x}{x^{2}-4}=-\dfrac{2x}{x^{2}-4}=-h(x)$

donc,

$h$ est impaire

$D_{k}=\mathbb{R}\setminus\{2\}$

$C_{1}\;:\;-2\in D_{k}\;\text{ or }2\notin D_{k}\;,\$ donc

$k$ n'est ni paire ni impaire.

VI.2 Centre de symétrie - axe de symétrie

VI.2.1 Centre de symétrie

$\centerdot\ \$ On dit que

$S\begin{pmatrix} a\\ b \end{pmatrix}$ est centre de symétrie pour

$\mathcal{C}_{f}$ si, et seulement si, les deux conditions suivantes sont vérifiées

$\left\{\begin{array}{lll} C_{1}\;:\;\text{ si }\;x\in D_{f}\;\text{ alors }2a-x\in D_{f}\\ C_{2}\;:\;\forall\; x\in D_{f}\;,\ f(2a-x)+f(x)=2b \end{array}\right.\quad\text{ ou }\;\left\{\begin{array}{lll} C_{1}\;:\;\text{ si }\;a-x\in D_{f}\;\text{ alors }a+x\in D_{f}\\ C_{2}\;:\;\forall\; x\in D_{f}\;,\ f(a+x)+f(a-x)=2b \end{array}\right.$

$\centerdot\ \$ On dit que

$S\begin{pmatrix} a\\ b \end{pmatrix}$ est centre de symétrie pour

$\mathcal{C}_{f}$ si, et seulement si, l'expression de

$\mathcal{C}_{f}$ dans le repère

$(S;\ \vec{i},\ \vec{j})$ est celle d'une fonction impaire.

Avec la formule de changement de repère, on aura

$\left\{\begin{array}{lcr} x=X+a\\ y=Y+b \end{array}\right.$

Exemple :

Soit

$f$ la fonction définie par

$f(x)=\dfrac{2x^{2}-5x-2}{x-3}$

Montrer que

$I\begin{pmatrix} 3\\ 7 \end{pmatrix}$ est le centre de symétrie.

Solution

1er méthode :

On a :

$D_{f}=\mathbb{R}\setminus\{3\}$

$C_{1}\;:$

$\begin{array}{rcl} 3-x\in D_{f} & \Rightarrow & 3-x\neq 3 \\ \\ & \Rightarrow & -x\neq 0 \\ \\ & \Rightarrow & x\neq 0 \\ \\ & \Rightarrow & x+3\neq 3 \\ \\ & \Rightarrow & 3+x\in D_{f} \end{array}$

$C_{2}\;:$

$\begin{array}{rcl} f(3-x)+f(3+x) & = & \dfrac{2(3-x)^{2}-5(3-x)-2}{(3-x)-3}+\dfrac{2(3+x)^{2}-5(3+x)-2}{(3+x)-3} \\ \\ & = & \dfrac{2x^{2}-12x+18-15+5x-2}{-x}+\dfrac{2x^{2}+12x+18-15-5x-2}{x} \\ \\ & = & \dfrac{-2x^{2}+7x-1+2x^{2}+7x+1}{x} \\ \\ & = & \dfrac{14x}{x} \\ \\ & = & 14 \\ \\ & = & 2\times 7) \end{array}$

donc,

$I$ est centre de symétrie pour

$\mathcal{C}_{f}$

2em méthode :

Soit

$f(x)=\dfrac{2x^{2}-5x-2}{x-3}=y$

En considérant le repère

$(I;\ \vec{i},\ \vec{j})$ , on aura

$\left\{\begin{array}{lcr} x=X+3\\ y=Y+7 \end{array}\right.$

Ce qui donne :

$\begin{array}{rcl} Y+7 & = & \dfrac{2(X+3)^{2}-5(X+3)-2}{(X+3)-3} \\ \\ & = & \dfrac{2X^{2}+12X+18-5X-15-2}{X} \\ \\ \Rightarrow\ Y & = & \dfrac{2X^{2}+12X+18-5X-15-2-7X}{X} \\ \\ & = & \dfrac{2X^{2}+1}{X} \end{array}$

$Y=\dfrac{2X^{2}+1}{X}\;\exists\;\Leftrightarrow\;X\neq 0$

Sur

$(I;\ \vec{i},\ \vec{j})$ , on a

$f(X)=\dfrac{2X^{2}+1}{X}$

$C_{1}\;:$

$\begin{array}{rcl} X\in D_{f} & \Rightarrow & X\neq 0 \\ \\ & \Rightarrow & -X\neq 0 \\ \\ & \Rightarrow & -X\in D_{f} \end{array}$

$C_{2}\;:\forall\;X\in D_{f}\;;\ f(-X)=\dfrac{2(-X)^{2}+1}{-X}=\dfrac{2X^{2}+1}{-X}=-\dfrac{2X^{2}+1}{X}=-f(X)$

donc,

$f$ est impaire ; d'où

$I$ est centre de symétrie.

VI.2.2 Axe de symétrie

$\centerdot\ \$ On dit que la droite d'équation

$x=a$ est axe de symétrie pour

$\mathcal{C}_{f}$ si, et seulement si, les deux conditions suivantes sont vérifiées

$\left\{\begin{array}{lll} C_{1}\;:\;\text{ si }\;x\in D_{f}\;\text{ alors }2a-x\in D_{f}\\ C_{2}\;:\;\forall\; x\in D_{f}\;,\ f(2a-x)=f(x)\end{array}\right.\quad\text{ ou }\;\left\{\begin{array}{lll} C_{1}\;:\;\text{ si }\;a+x\in D_{f}\;\text{ alors }a-x\in D_{f}\\ C_{2}\;:\;\forall\; x\in D_{f}\;,\ f(a+x)=f(a-x)\end{array}\right.$

$\centerdot\ \$ On dit que

$x=a$ est un axe de symétrie pour

$\mathcal{C}_{f}$ si, et seulement si, l'expression de

$\mathcal{C}_{f}$ dans le repère

$(S;\ \vec{i},\ \vec{j})$ où

$S\begin{pmatrix} a\\ b \end{pmatrix}$ est celle d'une fonction paire.

Exemple :

Soit

$f$ la fonction définie par

$f(x)=2x^{2}-5x+1$ .

Montrer que sa courbe représentative admet la droite d'équation

$x=\dfrac{5}{4}$ comme axe de symétrie

Solution

$D_{f}=\mathbb{R}$ , donc

$\forall\;x\in D_{f}\;,\ \dfrac{5}{4}+x\in D_{f}\;\text{ et }\dfrac{5}{4}-x\in D_{f}$

donc,

$C_{1}$ est vérifiée

pour la condition

$C_{2}$ on a :

$\begin{array}{rcl} f\left(\dfrac{5}{4}+x\right) & = & 2\left(\dfrac{5}{4}+x\right)^{2}-5\left(\dfrac{5}{4}+x\right)+1 \\ \\ & = & \dfrac{25}{8}+5x+2x^{2}-\dfrac{25}{4}-5x+1 \\ \\ & = & -\dfrac{17}{8}+2x^{2} \end{array}$

$\begin{array}{rcl} f\left(\dfrac{5}{4}-x\right) & = & 2\left(\dfrac{5}{4}-x\right)^{2}-5\left(\dfrac{5}{4}-x\right)+1 \\ \\ & = & \dfrac{25}{8}-5x+2x^{2}-\dfrac{25}{4}+5x+1 \\ \\ & = & -\dfrac{17}{8}+2x^{2} \end{array}$

Puisque

$f\left(\dfrac{5}{4}+x\right)=f\left(\dfrac{5}{4}-x\right)\;\forall\; x\in\mathbb{R}\;;\ C_{2}$ est vérifiée.

Donc la droite d'équation

$x=\dfrac{5}{4}$ est bien axe de symétrie pour

$\mathcal{C}_{f}.$

Remarques :

$\centerdot\ \$ Si

$f$ est paire, alors l'axe des ordonnées est un axe de symétrie.

Ainsi, pour étudier une fonction paire

$f$ , il suffit de l'étudier sur

$E=D_{f}\cap[0\;;\ +\infty[.$

$(\mathcal{C}_{f_{1}})$ est la courbe représentative de la restriction de

$f$ à

$E$ , la courbe

$(\mathcal{C}_{f})$ représentant les variations de la fonction

$f$ , s'obtient en complétant

$(\mathcal{C}_{f_{1}})$ par symétrie par rapport à l'axe

$y'Oy.$

$\centerdot\ \$ Si

$f$ est impaire, alors l'origine du repère

$(O)$ est le centre de symétrie.

Ainsi, pour étudier une fonction impaire

$f$ , il suffit de l'étudier sur

$E=D_{f}\cap[0\;;\ +\infty[.$

$(\mathcal{C}_{f_{1}})$ est la courbe représentative de la restriction de

$f$ à

$E$ , la courbe

$(\mathcal{C}_{f})$ représentant les variations de la fonction

$f$ , s'obtient en complétant

$(\mathcal{C}_{f_{1}})$ par symétrie par rapport à l'origine

$O.$

$\centerdot\ \$ Pour étudier une fonction admettant le point

$S\begin{pmatrix} a\\ b \end{pmatrix}$ comme centre de symétrie, il suffit de l'étudier sur

$E=D_{f}\cap[a\;;\ +\infty[.$

$(\mathcal{C}_{f_{1}})$ est la courbe représentative de la restriction de

$f$ à

$E$ , la courbe

$(\mathcal{C}_{f})$ représentant les variations de la fonction

$f$ , s'obtient en complétant

$(\mathcal{C}_{f_{1}})$ par symétrie par rapport au point

$S\begin{pmatrix} a\\ b \end{pmatrix}.$

$\centerdot\ \$ Pour étudier une fonction admettant la droite d'équation

$x=a$ comme axe de symétrie de la courbe représentative de

$f$ , il suffit de l'étudier sur

$E=D_{f}\cap[a\;;\ +\infty[.$

$(\mathcal{C}_{f_{1}})$ est la courbe représentative de la restriction de

$f$ à

$E$ , la courbe

$(\mathcal{C}_{f})$ représentant les variations de la fonction

$f$ , s'obtient en complétant

$(\mathcal{C}_{f_{1}})$ par symétrie par rapport à l'axe

$x=a.$

$\centerdot\ \$ Pour un axe de symétrie, il est nécessaire que le repère soit orthogonal.

$\centerdot\ \$ Attention! La plupart des fonctions ne sont ni paires, ni impaires et donc n'admettent ni axe de symétrie, ni centre de symétrie.

$\centerdot\ \$ Toute fonction

$f$ définie sur une partie

$E$ de

$\mathbb{R}$ admettant le point

$(O)$ pour centre de symétrie est la somme d'une fonction paire et d'une fonction impaire et cette décomposition est unique.

En effet : si

$f=g+h$ où

$g$ est paire et

$h$ est impaire, on a

$f(x)=g(x)+h(x)\;$ et

$\;f(-x)=g(x)-h(x)$

d'où,

$g(x)=\dfrac{1}{2}\left[f(x)+f(-x)\right]\;\text{ et }\;h(x)=\dfrac{1}{2}\left[f(x)-f(-x)\right]$

Réciproquement, les fonctions

$g$ et

$h$ ainsi déterminées à partir de

$f$ sont respectivement paire et impaire et vérifient

$f=g+h.$

Exemple :

Soit

$f$ la fonction définie sur

$\mathbb{R}$ par

$f(x)=2x^{3}+5x^{2}-x+1.$

Cette fonction

$f$ est la somme

$-\$ de la fonction

$g$ paire

$g:\:x\longmapsto 5x^{2}+1$

$-\$ et de la fonction

$h$ impaire

$h:\:x\longmapsto -2x^{3}-x$

VI.3 Périodicité

$\centerdot\ \$ On dit qu'une fonction

$f$ est périodique de période

$T$ si, et seulement si, les deux conditions suivantes sont vérifiées

$\left\{\begin{array}{lll} C_{1}\;:\;\text{ si }\;x\in D_{f}\;\text{ alors }x+T\in D_{f}\\ C_{2}\;:\;\forall\; x\in D_{f}\;,\ f(x+T)=f(x) \end{array}\right.$

$\centerdot\ \$ Si

$T$ est une période pour

$f$ , tout multiple de

$T$ non nul (c'est-à-dire

$2T$ ,

$3T$ ,

$4T$ ...) est aussi une période pour

$f$ . Dans les cas usuels, l'une des périodes positives est plus petite que toutes les autres, c'est ce nombre qui est appelé plus précisément période de la fonction

$f$ et sera noté

$T$ (et par conséquent

$T$ doit être le plus petit possible)

$\centerdot\ \$ Pour

$\omega\neq 0$ , on reconnait la période des fonctions trigonométriques suivantes :

$-\$ la fonction

$x\longmapsto\cos(\omega x+\varphi)$ admet pour période

$T=\dfrac{2\pi}{|\omega|}$

$-\$ la fonction

$x\longmapsto\sin(\omega x+\varphi)$ admet pour période

$T=\dfrac{2\pi}{|\omega|}$

$-\$ la fonction

$x\longmapsto\tan(\omega x+\varphi)$ admet pour période

$T=\dfrac{\pi}{|\omega|}$

Exemple :

Déterminer les périodes des fonctions suivantes :

$f(x)=\sin 2x\;,\ g(x)=\sin\left(3x+\dfrac{\pi}{5}\right)\;,\ h(x)=\cos\left(\dfrac{x}{3}\right)$

$k(x)=4\sin 3x+5\cos 2x\;,\ m(x)=\tan 3x\;,\ \kappa(x)=\cos^{2} x$

Solution

la fonction

$f$ a pour période

$T=\dfrac{2\pi}{2}=\pi$

la fonction

$g$ a pour période

$T=\dfrac{2\pi}{3}$

la fonction

$h$ a pour période

$T=\dfrac{2\pi}{\dfrac{1}{3}}=6\pi$

la fonction

$k(x)=4\sin 3x+5\cos 2x$ est la somme de deux fonctions de périodes respectives

$T_{1}=\dfrac{2\pi}{3}$ et

$T_{2}=\pi$

donc

$3T_{1}=2\pi$ et

$T_{2}=\pi$ sont aussi des périodes respectives de

$\sin 3x$ et

$\cos 2x$

alors le

$PPCM$ de

$3T_{1}$ et de

$T_{2}$ est à la fois période de

$\sin 3x$ et de

$\cos 2x$

ainsi,

$T=PPCM(2\pi\;;\ \pi)=2\pi$ est la période de la fonction

$k$

la fonction

$m$ a pour période

$T=\dfrac{\pi}{3}$

Pour déterminer la période de la fonction

$\kappa(x)=\cos^{2} x$ , il est nécessaire de linéariser cette expression trigonométrique, puisque

$\cos^{2} x=\dfrac{1+\cos 2x}{2}$ , l fonction

$\kappa$ admet pour période

$T=\dfrac{2\pi}{2}=\pi$

Remarques :

Pour étudier une fonction

$f$ de période

$T$ , il suffit de l'envisager sur

$E=D_{f}\cap[\alpha\;;\ \alpha +T[$ avec

$\alpha$ réel quelconque.

$(\mathcal{C}_{f_{1}})$ est la courbe représentative de la restriction de

$f$ à

$E$ , la courbe

$(\mathcal{C})$ représentant les variations de la fonction

$f$ , s'obtient en complétant

$(\mathcal{C}_{f_{1}})$ par les arcs de courbe qui s'en déduisent par les translations de vecteur

$k\vec{u}$ avec

$k\in\mathbb{R}$ et

$\vec{u}\begin{pmatrix} T\\ 0 \end{pmatrix}$

VII Variation d'une fonction

VII.1 Taux de variation

On appelle taux de variation d'une fonction

$f$ de

$x_{1}$ à

$x_{2}$ noté

$T^{x_{2}}_{x_{1}}$ , le rapport entre

$(f(x_{2})-f(x_{1}))$ et

$(x_{2}-x_{1})$

On a

$T^{x_{2}}_{x_{1}}=\dfrac{f(x_{2})-f(x_{1})}{x_{2}-x_{1}}$

Exemple :

Calculer les taux de variation des fonctions suivantes :

$f(x)=x^{3}\;,\ g(x)=x^{2}\;,\ h(x)=\dfrac{x^{2}-4x+4}{x-1}$

Solution

$f(x)=x^{3}$ , on a

$D_{f}=\mathbb{R}\$ et

$\begin{array}{rcl} T^{x_{2}}_{x_{1}} & = & \dfrac{f(x_{2})-f(x_{1})}{x_{2}-x_{1}} \\ \\ & = & \dfrac{x_{2}^{3}-x_{1}^{3}}{x_{2}-x_{1}} \\ \\ & = & \dfrac{(x_{2}-x_{1})(x_{2}^{2}+x_{2}x_{1}+x_{1}^{2})}{x_{2}-x_{1}} \\ \\ & = & x_{2}^{2}+x_{2}x_{1}+x_{1}^{2} \end{array}$

$g(x)=x^{2}\;,\ D_{g}=\mathbb{R}$

on a :

$\begin{array}{rcl} T^{x_{2}}_{x_{1}} & = & \dfrac{f(x_{2})-f(x_{1})}{x_{2}-x_{1}} \\ \\ & = & \dfrac{x_{2}^{2}-x_{1}^{2}}{x_{2}-x_{1}} \\ \\ & = & \dfrac{(x_{2}-x_{1})(x_{2}+x_{1})}{x_{2}-x_{1}} \\ \\ & = & x_{2}+x_{1} \end{array}$

$h(x)=\dfrac{x^{2}-4x+4}{x-1}\;,\ D_{h}=\mathbb{R}\setminus\{1\}$

on a :

$\begin{array}{rcl} T^{x_{2}}_{x_{1}} & = & \dfrac{f(x_{2})-f(x_{1})}{x_{2}-x_{1}} \\ \\ & = & \dfrac{\dfrac{x_{2}^{2}-4x_{2}+4}{x_{2}-1}-\dfrac{x_{1}^{2}-4x_{1}+4}{x_{1}-1}}{x_{2}-x_{1}} \\ \\ & = & \dfrac{x_{1}x_{2}^{2}-4x_{2}x_{1}+4x_{1}-x_{2}^{2}+4x_{2}-4-x_{1}^{2}x_{2}+4x_{2}x_{1}-4x_{2}+x_{1}^{2}-4x_{1}+4}{(x_{2}-1)(x_{1}-1)(x_{2}-x_{1})} \\ \\ & = & \dfrac{x_{1}x_{2}^{2}-x_{2}^{2}-x_{1}^{2}x_{2}+x_{1}^{2}}{(x_{2}-1)(x_{1}-1)(x_{2}-x_{1})} \\ \\ & = & \dfrac{x_{1}x_{2}(x_{2}-x_{1})-(x_{2}-x_{1})(x_{2}+x_{1})}{(x_{2}-1)(x_{1}-1)(x_{2}-x_{1})} \\ \\ & = & \dfrac{(x_{2}-x_{1})(x_{1}x_{2}-x_{2}-x_{1})}{(x_{2}-1)(x_{1}-1)(x_{2}-x_{1})} \\ \\ & = & \dfrac{x_{1}x_{2}-x_{2}-x_{1}}{(x_{2}-1)(x_{1}-1)} \\ \\ & = & 1-\dfrac{1}{(x_{2}-1)(x_{1}-1)} \end{array}$

VII.2 Définition

Soit

$I$ un intervalle de

$\mathbb{R}$

$\centerdot\ \$ On dit qu'une fonction

$f$ est croissante sur

$I$ si, et seulement si,

$\forall\; x\;,\; y\; \in I\;;\ \text{ si } x\leq y\; \Rightarrow\; f(x)\leq f(y)\quad\text{ (ou si }x\geq y\; \Rightarrow\; f(x)\geq f(y))$

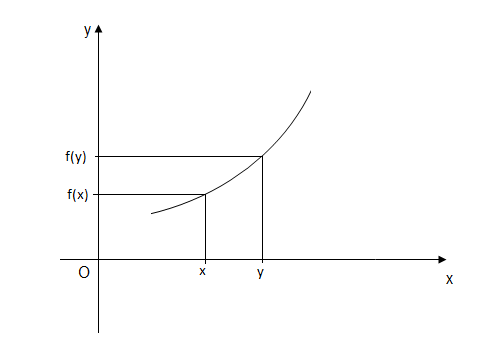
$\centerdot\ \$ On dit qu'une fonction

$f$ est décroissante sur

$I$ si, et seulement si,

$\forall\; x\;,\; y\; \in I\;;\ \text{ si } x\leq y\; \Rightarrow\; f(x)\geq f(y)\quad\text{ (ou si }x\geq y\; \Rightarrow\; f(x)\leq f(y))$

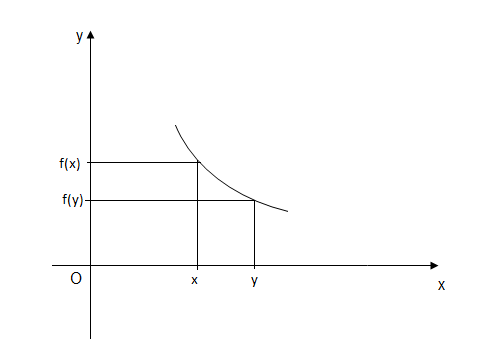
$\centerdot\ \$ On dit qu'une fonction

$f$ est constante sur

$I$ si, et seulement si,

$\forall\; x\;,\; y\; \in I\;;\ f(x)=f(y)$

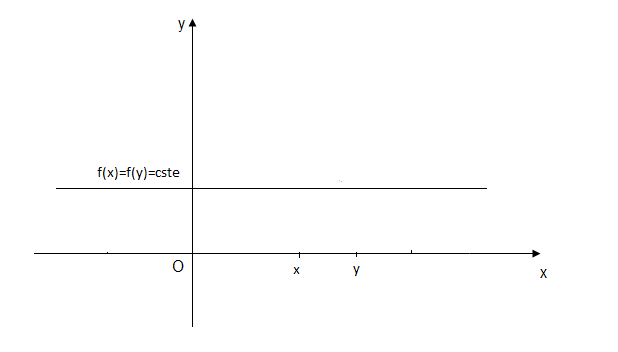
VII.3 Propriétés

Soit

$I$ un intervalle de

$\mathbb{R}\;;\ x_{1}\;,\ x_{2}\;\in I$

Soit

$T^{x_{2}}_{x_{1}}=\dfrac{f(x_{2})-f(x_{1})}{x_{2}-x_{1}}$ le taux de variation de

$x_{1}$ à

$x_{2}$ , d'une fonction

$f.$

$\centerdot\ \$ Si

$f\text{ est croissante }(\nearrow)$ alors on a :

$\text{ si } x_{1}\leq x_{2}\; \Rightarrow\; f(x_{1})\leq f(x_{2})\;\text{ ou si }x_{1}\geq x_{2}\; \Rightarrow\; f(x_{1})\geq f(x_{2})$

Ainsi,

$(x_{2}-x_{1})\;\text{ et }(f(x_{2}))$ ont même signe

Donc,

$T^{x_{2}}_{x_{1}}\geq 0$

$\centerdot\ \$ Si

$f\text{ est décroissante }(\searrow)$ alors on a :

$\text{ si } x_{1}\leq x_{2}\; \Rightarrow\; f(x_{1})\geq f(x_{2})\;\text{ ou si }x_{1}\geq x_{2}\; \Rightarrow\; f(x_{1})\leq f(x_{2})$

Ainsi,

$(x_{2}-x_{1})\;\text{ et }(f(x_{2})-f(x_{1}))$ sont toujours de signes contraires.

Donc,

$T^{x_{2}}_{x_{1}}\leq 0$

En conclusion on a :

$-\$ Si

$T^{x_{2}}_{x_{1}}\geq 0$ sur un intervalle

$I$ alors

$f\text{ est }\nearrow$ sur

$I.$

$-\$ Si

$T^{x_{2}}_{x_{1}}\leq 0$ sur un intervalle

$I$ alors

$f\text{ est }\searrow$ sur

$I.$

VII.4 Tableau de variation

a) Soit

$f$ la fonction définie sur

$\mathbb{R}$ par

$f(x)=x^{2}.$

Montrer que

$f\nearrow$ sur

$[0\;;\ +\infty[$ et

$f\searrow$ sur

$]-\infty\;;\ 0].$

Soit

$T^{x_{2}}_{x_{1}}=x_{2}+x_{1}$

On a :

$-\$ sur

$[0\;;\ +\infty[\;,\ x_{1}\geq 0\;\text{ et }x_{2}\geq 0$

alors,

$x_{2}+x_{1}\geq 0\; \Rightarrow\; T^{x_{2}}_{x_{1}}\geq 0$

donc,

$f\; \text{ est croissante sur }[0\;;\ +\infty[$

$-\$ et sur

$]-\infty\;;\ 0]\;,\ x_{1}\leq 0\;\text{ et }x_{2}\leq 0$

alors,

$x_{2}+x_{1}\leq 0\; \Rightarrow\; T^{x_{2}}_{x_{1}}\leq 0$

donc,

$f\; \text{ est décroissante sur }]-\infty\;;\ 0]$

Enfin, les variations de

$f$ sont représentées dans le tableau ci-après, souvent appelé tableau des variations de

$f$

$\begin{array}{|c|lcccr|}\hline x & -\infty & & 0 & & +\infty\\ \hline & & & & & \\ f & & \searrow & & \nearrow & \\ & & & 0 & & \\ \hline\end{array}$

b) Soit

$g$ la fonction définie sur

$\mathbb{R}$ par

$g(x)=x^{2}-4x+3.$

Montrer que

$g\nearrow$ sur

$[2\;;\ +\infty[$ et

$g\searrow$ sur

$]-\infty\;;\ 2].$

En effet,

$\begin{array}{rcl} T^{x_{2}}_{x_{1}} & = & \dfrac{g(x_{2})-g(x_{1})}{x_{2}-x_{1}} \\ \\ & = & \dfrac{x_{2}^{2}-4x_{2}+3-x_{1}^{2}+4x_{1}-3}{x_{2}-x_{1}} \\ \\ & = & \dfrac{x_{2}^{2}-x_{1}^{2}-4x_{2}+4x_{1}}{x_{2}-x_{1}} \\ \\ & = & \dfrac{(x_{2}-x_{1})(x_{2}+x_{1})-4(x_{2}-x_{1})}{x_{2}-x_{1}} \\ \\ & = & \dfrac{(x_{2}-x_{1})[(x_{2}+x_{1})-4]}{x_{2}-x_{1}} \\ \\ & = & x_{2}+x_{1}-4 \end{array}$

donc,

$T^{x_{2}}_{x_{1}}=x_{2}+x_{1}-4$

ainsi, sur

$[2\;;\ +\infty[\;,\ x_{1}\geq 2\;\text{ et }x_{2}\geq 2$

alors

$x_{2}+x_{1}-4\geq 0\; \Rightarrow\; T^{x_{2}}_{x_{1}}\geq 0$

d'où,

$g\; \text{ est croissante sur }[2\;;\ +\infty[$

et sur

$]-\infty\;;\ 2]\;,\ x_{1}\leq 2\;\text{ et }x_{2}\leq 2$

donc,

$x_{2}+x_{1}-4\leq 0\; \Rightarrow\; T^{x_{2}}_{x_{1}}\leq 0$

d'où,

$g\; \text{ est décroissante sur }]-\infty\;;\ 2]$

Enfin, les variations de

$g$ sont représentées dans le tableau ci-après

$\begin{array}{|c|lcccr|}\hline x & -\infty & & 2 & & +\infty\\ \hline & & & & & \\ g & & \searrow & & \nearrow & \\ & & & -1 & & \\ \hline\end{array}$

VIII Courbe d'une fonction - fonctions associées

VIII.1 Graphe de $x^{2}\;,\ \dfrac{1}{x}\;,\ \sqrt{x}$ et de $x^{3}$

Le graphe d'une fonction

$f$ est l'ensemble des points

$M\begin{pmatrix} x\\ y \end{pmatrix}$ du plan vérifiant

$x\in D_{f}$ et

$y=f(x)$

On note

$(\mathcal{C}_{f})=\left\{M\begin{pmatrix} x\\ y \end{pmatrix}\;\text{ tel que }x\in D_{f}\;\text{ et }y=f(x)\right\}$

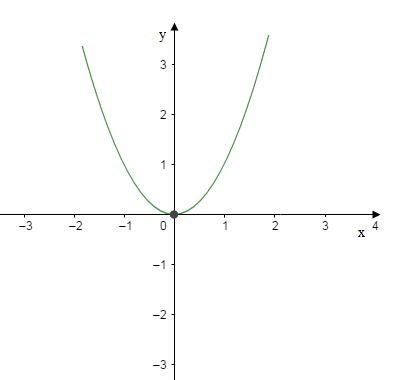
a) Soit

$f(x)=x^{2}\;,\ D_{f}=\mathbb{R}$

$-\$ Parité

$f$ est paire, alors l'axe des ordonnées est un axe de symétrie.

Donc on peut étudier

$f$ sur

$[0\;;\ +\infty[.$

$-\$ Monotonie

Soit

$T^{x_{2}}_{x_{1}}=x_{2}+x_{1}$

On a :

sur

$[0\;;\ +\infty[\;,\ x_{1}\geq 0\;\text{ et }x_{2}\geq 0$

alors

$x_{2}+x_{1}\geq 0\; \Rightarrow\; T^{x_{2}}_{x_{1}}\geq 0$

donc

$f\; \text{ est croissante sur }[0\;;\ +\infty[$

$-\$ Tableau de variation

$\begin{array}{|c|lcr|}\hline x & 0 & & +\infty\\ \hline T^{x_{2}}_{x_{1}} & & + & \\ \hline & & & \\ f & & \nearrow & \\ & 0 & & \\ \hline\end{array}$

$-\$ Graphe

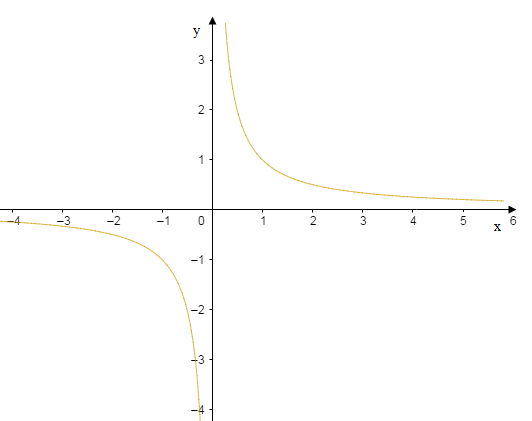
b) Soit

$g(x)=\dfrac{1}{x}\;,\ D_{g}=\mathbb{R}\setminus\{0\}$

$-\$ Parité

$C_{1}\;:$

$\begin{array}{rcl} x\in D_{g} & \Rightarrow & x\neq 0 \\ \\ & \Rightarrow & -x\neq 0 \\ \\ & \Rightarrow & -x\in D_{g} \end{array}$

$C_{2}\;:\forall\;x\in D_{f}\;;\ g(-x)=\dfrac{1}{-x}=-\dfrac{1}{x}=-g(x)$

donc

$g$ est impaire ; d'où

$O$ est centre de symétrie.

Ainsi, on pourra étudier la fonction

$g$ sur

$]0\;;\ +\infty[.$

$-\$ Monotonie

On a

$\begin{array}{rcl} T^{x_{2}}_{x_{1}} & = & \dfrac{g(x_{2})-g(x_{1})}{x_{2}-x_{1}} \\ \\ & = & \dfrac{\dfrac{1}{x_{2}}-\dfrac{1}{x_{1}}}{x_{2}-x_{1}} \\ \\ & = & \dfrac{x_{1}-x_{2}}{x_{1}x_{2}(x_{2}-x_{1})} \\ \\ & = & \dfrac{-(x_{2}-x_{1})}{x_{1}x_{2}(x_{2}-x_{1})} \\ \\ & = & -\dfrac{1}{x_{1}x_{2}} \end{array}$

sur

$]0\;;\ +\infty[\;,\ x_{1}\geq 0\;\text{ et }x_{2}\geq 0$

alors,

$x_{1}x_{2}\geq 0\; \Rightarrow\; \dfrac{1}{x_{1}x_{2}}\geq 0$

donc,

$T^{x_{2}}_{x_{1}}=-\dfrac{1}{x_{1}x_{2}}\leq 0$

d'où,

$g\; \text{ est décroissante sur }]0\;;\ +\infty[$

$-\$ Tableau de variation

$\begin{array}{|c||lcr|}\hline x & 0 & & +\infty\\ \hline T^{x_{2}}_{x_{1}} & & - & \\ \hline & & & \\ g & & \searrow & \\ & & & \\ \hline\end{array}$

$-\$ Graphe

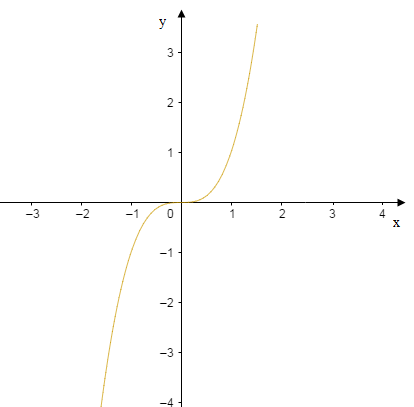
c) Soit

$h(x)=x^{3}\;,\ D_{h}=\mathbb{R}$

$-\$ Parité

$h$ est impaire, donc le point

$O$ est centre de symétrie.

Ainsi, l'étude de

$h$ peut se faire sur

$[0\;;\ +\infty[.$

$-\$ Monotonie

Soit

$T^{x_{2}}_{x_{1}}=x_{2}^{2}+x_{2}x_{1}+x_{1}^{2}$

On a :

sur

$[0\;;\ +\infty[\;,\ x_{1}\geq 0\;\text{ et }x_{2}\geq 0$

alors,

$x_{2}^{2}+x_{2}x_{1}+x_{1}^{2}\geq 0\; \Rightarrow\; T^{x_{2}}_{x_{1}}\geq 0$

donc,

$h\; \text{ est croissante sur }[0\;;\ +\infty[$

$-\$ Tableau de variation

$\begin{array}{|c|lcr|}\hline x & 0 & & +\infty\\ \hline T^{x_{2}}_{x_{1}} & & + & \\ \hline & & & \\ h & & \nearrow & \\ & 0 & & \\ \hline \end{array}$

$-\$ Graphe

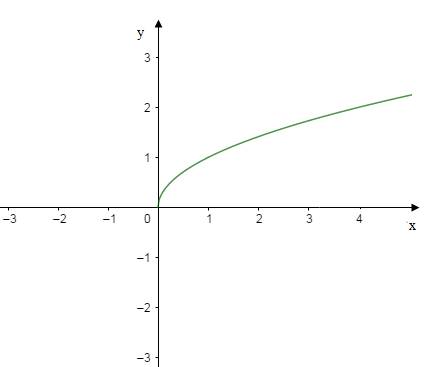
d) Soit

$k(x)=\sqrt{x}\;,\ D_{k}=[0\;;\ +\infty[.$

$-\$ Parité

$k$ n'est ni paire ni impaire ; la condition

$C_{1}$ n'est pas vérifiée.

$-\$ Monotonie

On a :

$\begin{array}{rcl} T^{x_{2}}_{x_{1}} & = & \dfrac{k(x_{2})-k(x_{1})}{x_{2}-x_{1}} \\ \\ & = & \dfrac{\sqrt{x_{2}}-\sqrt{x_{1}}}{\sqrt{x_{2}^{2}}-\sqrt{x_{1}^{2}}} \\ \\ & = & \dfrac{\sqrt{x_{2}}-\sqrt{x_{1}}}{(\sqrt{x_{2}}-\sqrt{x_{1}})(\sqrt{x_{2}}+\sqrt{x_{1}})} \\ \\ & = & \dfrac{1}{\sqrt{x_{2}}+\sqrt{x_{1}}} \end{array}$

sur

$[0\;;\ +\infty[\;,\ x_{1}\geq 0\;\text{ et }x_{2}\geq 0$

alors,

$\sqrt{x_{2}}+\sqrt{x_{1}}\geq 0\; \Rightarrow\; \dfrac{1}{\sqrt{x_{2}}+\sqrt{x_{1}}}\geq 0$

donc,

$T^{x_{2}}_{x_{1}}\geq 0$

d'où,

$k\; \text{ est croissante sur } [0\;;\ +\infty[$

$-\$ Tableau de variation

$\begin{array}{|c|lcr|}\hline x & 0 & & +\infty\\ \hline T^{x_{2}}_{x_{1}} & & + & \\ \hline & & & \\ k & & \nearrow & \\ & 0 & & \\ \hline \end{array}$

$-\$ Graphe

VIII.2 Fonctions associées

Soit

$f$ une fonction définie sur une partie

$I$ de

$\mathbb{R}.$

Les fonctions

$g\;,\ h\;,\ k\;,\ m$ et

$\ell$ définies par :

$g(x)=-f(x)\;,\ h(x)=|f(x)|\;,\ k(x)=f(x)+a\;,\ m(x)=f(x-a)$ et

$\ell(x)=f(x-a)+b$ sont appelées fonctions associées à

$f.$

$g(x)=-f(x)$

Soient

$M\begin{pmatrix} x\\ f(x)\end{pmatrix}$ et

$M'\begin{pmatrix} x\\ g(x)=-f(x) \end{pmatrix}$ deux points du plan.

Alors

$M$ et

$M'$ sont symétriques par rapport à l'axe des abscisses

$(x'Ox).$

Donc

$\mathcal{C}_{g}$ et

$\mathcal{C}_{f}$ sont symétriques par rapport à

$(x'Ox).$

$h(x)=|f(x)|$

On a

$h(x)=\left\{\begin{array}{lcl} f(x)\;\text{ si }\;f(x) &\geq & 0\;\Rightarrow\;\mathcal{C}_{g}=\mathcal{C}_{f}\\ -f(x)\;\text{ si }\;f(x) &\leq & 0\;\Rightarrow\;\mathcal{C}_{g}\;\text{ est symétrique de }\mathcal{C}_{f}\;\text{ par rapport à }(x'Ox) \end{array}\right.$

$k(x)=f(x)+a$

Soient

$M\begin{pmatrix} x\\ f(x) \end{pmatrix}$ et

$M'\begin{pmatrix} x\\ f(x)+a \end{pmatrix}$ deux points du plan.

On a

$\overrightarrow{MM'}\begin{pmatrix} 0\\ a \end{pmatrix}\;\Rightarrow\;\overrightarrow{MM'}=a.\vec{j}$

donc

$M'=t_{a.\vec{j}}(M)$

Ainsi,

$\mathcal{C}_{k}$ est l'image de

$\mathcal{C}_{f}$ par la translation de vecteur

$a.\vec{j}.$

Par exemple, si

$k(x)=f(x)+2$ , alors

$\mathcal{C}_{k}$ est l'image de

$\mathcal{C}_{f}$ par la translation de vecteur

$2\vec{j}.$

$m(x)=f(x-a)$

Soient

$M\begin{pmatrix} x\\ f(x) \end{pmatrix}$ et

$M'\begin{pmatrix} x+a\\ m(x+a)=f(x) \end{pmatrix}$ deux points du plan.

On a

$\overrightarrow{MM'}\begin{pmatrix} a\\ 0 \end{pmatrix}\;\Rightarrow\;\overrightarrow{MM'}=a.\vec{i}$

donc

$M'=t_{a.\vec{i}}(M)$

Ainsi,

$\mathcal{C}_{m}$ est l'image de

$\mathcal{C}_{f}$ par la translation de vecteur

$a.\vec{i}.$

Exemple :

$m(x)=f(x-2)$ , donc

$\mathcal{C}_{m}$ est l'image de

$\mathcal{C}_{f}$ par la translation de vecteur

$2\vec{i}.$

$\ell(x)=f(x-a)+b$

$M\begin{pmatrix} x-a\\ f(x-a) \end{pmatrix}$ et

$M'\begin{pmatrix} x\\ f(x-a)+b \end{pmatrix}$ deux points donnés.

Alors

$\overrightarrow{MM'}\begin{pmatrix} a\\ b \end{pmatrix}\;\Rightarrow\;\overrightarrow{MM'}=a.\vec{i}+b.\vec{j}$

donc

$M'$ est l'image de

$M$ par la translation de vecteur

$a.\vec{i}+b.\vec{j}\;;\ M'=t_{a.\vec{i}+b.\vec{j}}(M)$

d'où,

$\mathcal{C}_{\ell}$ est l'image de

$\mathcal{C}_{f}$ par la translation de vecteur

$a.\vec{i}+b.\vec{j}.$

Exemple

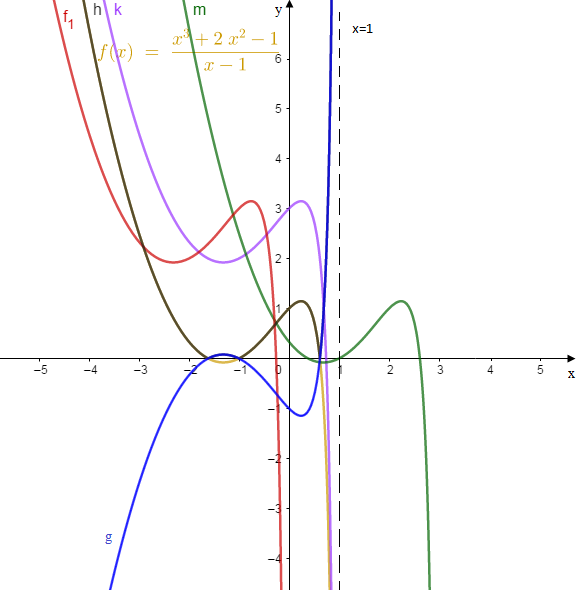
Soit

$f$ la fonction définie sur

$\mathbb{R}\setminus\{1\}$ par :

$f(x)=\dfrac{x^{3}+2x^{2}-1}{x-1}$

Représenter

$\mathcal{C}_{g}\;,\ \mathcal{C}_{h}\;,\ \mathcal{C}_{k}\;,\ \mathcal{C}_{m}$ et

$\mathcal{C}_{f_{1}}$ les courbes respectives des fonctions

$g\;,\ h\;,\ k\;,\ m$ et

$f_{1}$ définies par :

$g(x)=-f(x)\;,\ h(x)=|f(x)|\;,\ k(x)=f(x)+2\;,\ m(x)=f(x-2)$ et

$f_{1}(x)=f(x+1)+2$

Solution

Auteur:

Diny Faye & Seyni Ndiaye

Commentaires

Mor talla Cissé (non vérifié)

jeu, 09/05/2019 - 20:19

Permalien

J'aime ce site

répondre

Anonyme (non vérifié)

jeu, 12/09/2021 - 23:36

Permalien

Excellent travail

répondre

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Généralités sur les fonctions - 1er S

Formulaire de recherche

I Définition de fonctions et applications

I.1 Définition

Notation

I.2 Ensemble de définition

Exemple 1 :

Exemple 2 :

Solution

Remarque :

I.3 Courbe représentative d'une fonction

I.4 Application

I.4.1 Définition

Remarque :

I.4.2 Applications injectives, surjectives, bijectives

a) Application injective ou injection

Remarque :

b) Théorème de caractérisation de l'injection

Exemple :

c) Application surjective ou surjection

Exemple :

d) Application bijective ou bijection

e) Théorème de caractérisation

II Opérations sur les fonctions

II.1 Égalité de deux fonctions

II.2 Somme de deux fonctions

Exemple :

II.3 Produit d'une fonction par un réel

II.4 Produit de deux fonctions

Exemple :

Remarque :

Exemple :

II.5 Quotient de deux fonctions

Exemple :

Remarque :

III Composition de deux fonctions

Exemple :

Exemple :

Propriété :

Exemple :

Attention !

Exemple :

IV Les formules de changement de repère (par translation)

V Restriction et prolongement d'une fonction

Exemple :

Exemple :

VI Parité et éléments de symétrie

VI.1 Parité d'une fonction

Exemple :

Solution

VI.2 Centre de symétrie - axe de symétrie

VI.2.1 Centre de symétrie

Exemple :

Solution

VI.2.2 Axe de symétrie

Exemple :

Solution

Remarques :

Exemple :

VI.3 Périodicité

Exemple :

Solution

Remarques :

VII Variation d'une fonction

VII.1 Taux de variation

Exemple :

Solution

VII.2 Définition

VII.3 Propriétés

VII.4 Tableau de variation

VIII Courbe d'une fonction - fonctions associées

VIII.1 Graphe de x2, 1x, √xx^{2}\;,\ \dfrac{1}{x}\;,\ \sqrt{x} et de x3x^{3}

VIII.2 Fonctions associées

Exemple :

Exemple

Solution

Commentaires

J'aime ce site

Excellent travail

VIII.1 Graphe de $x^{2}\;,\ \dfrac{1}{x}\;,\ \sqrt{x}$ et de $x^{3}$