Vous êtes ici

Série d'exercices : Généralité sur les champs magnétiques - Champs magnétique des courants - Ts

Classe:

Terminale

Exercice 1

1) Représenter le spectre de l'aimant représenté ci-dessous.

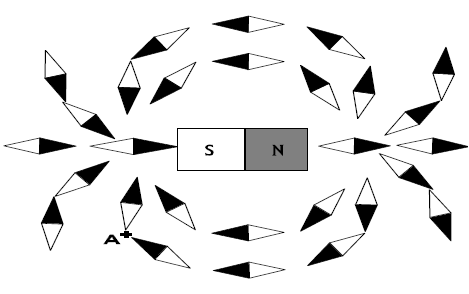
2) On place au point $A$ un capteur de champ magnétique, de sensibilité : $20\,mV/mT.$

Celui-ci indique $227\,mV.$

a) Calculer l'intensité du champ magnétique au point $A.$

b) Tracer le vecteur champ magnétique en ce point.

Exercice 2

1) Tracer le spectre de l'aimant en $U$ entre les deux pôles.

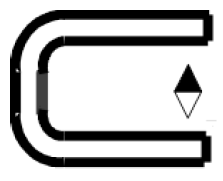
2) Orienter les lignes de champ.

3) Identifier les pôles de cet aimant.

4) Quelle propriété possède le vecteur $B$ dans cette région de l'espace champ magnétique ?

Comment appelle-t-on un tel champ magnétique ?

Exercice 3

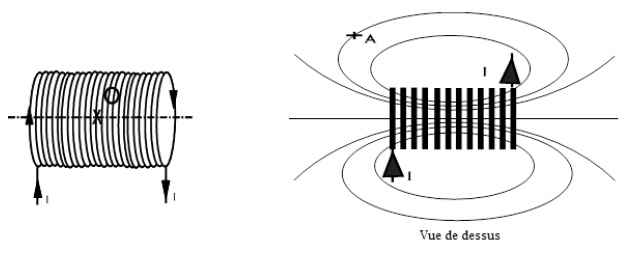
Soit un solénoïde de longueur $L=50\,cm$, constitué de $2000$ spires et parcouru par un courant d'intensité $1.5\,A.$

1) Identifier les pôles de ce solénoïde.

2) Calculer la norme du champ magnétique créé au centre de ce solénoïde.

3) Représenter le vecteur champ magnétique en ce point.

4) La norme du champ en $A$ est de $0.5\,mT.$

Représenter le vecteur champ magnétique en $A.$

Exercice 4

Deux aimants droits $A_{1}$ et $A_{2}$ sont placés sur l'axe $x'x.$

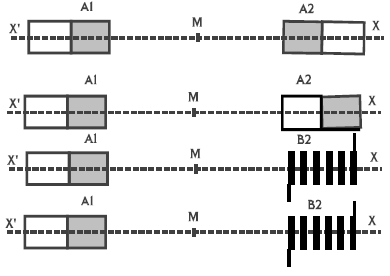
Chacun d'eux crée au point $M$ situé à égale distance des deux sources, un champ magnétique de $20\,mT.$

1) Représenter le vecteur champ magnétique en $M$, lorsque les deux pôles en regard sont de même nom.

2) Même question lorsque les deux pôles sont de noms différents.

3) On remplace l'aimant $A_{2}$ par une bobine $B_{2}.$

On désire qu'au point $M$ le champ résultant ait une norme égale à $60\,mT.$

Quelle doit être la norme du champ magnétique créé par la bobine ?

(Deux cas sont envisageables).

Pour chaque cas, quel est le sens du courant dans la bobine ?

Exercice 5

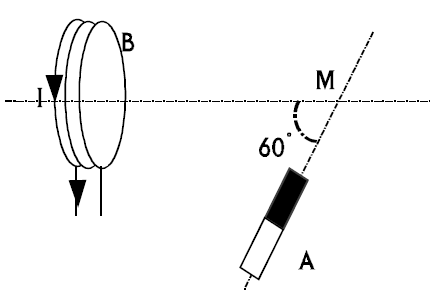
Une bobine parcourue par un courant d'intensité $I$, crée en $M$ un champ magnétique de norme $B_{1}=2\,mT.$

Un aimant $A$ crée en $M$ un champ magnétique de norme $B_{2}=4\,mT.$

1) Représenter les vecteurs champ magnétique créés en $M$ par chacune des deux sources.

2) Représenter le vecteur champ magnétique résultant.

Déterminer sa norme.

Exercice 6

A l'intérieur d'un solénoïde $S_{1}$ comportant $n_{1}$ Spires par mètre, parcouru par un courant d'intensité $I_{1}$, on place un solénoïde $S_{2}$ dont l'axe est orthogonal à celui de $S_{1}$, comportant $n_{2}$ spires par mètre et parcouru par un courant $I_{2}.$

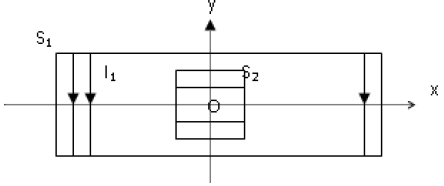
1) $I_{2}=0$ ; Représenter le vecteur induction magnétique $B_{1}$ au centre de $S_{1}$ et exprimer son intensité en fonction de $n_{1}$ et $I_{1}.$

2) $I_{2}\neq 0$ ; indiquer en le justifiant, le sens de $I_{2}$ pour que le vecteur induction $B_{2}$ crée au centre de $S_{2}$ ait le même sens que l'axe $(y'y).$

3) Une petite aiguille aimantée, placée au centre $O$ des deux solénoïdes prend une direction $\alpha$ avec l'axe $(x'x).$

a) Faire un schéma clair dans lequel sont représentés les vecteurs $B_{1}$, $B_{2}$ et l'aiguille.

b) Exprimer le rapport $n_{2}/n_{1}$ en fonction de $\alpha$, $I_{1}$ et $I_{2}.$

c) Calculer $n_{1}$ et $n_{2}$ sachant que $n_{1}+n_{2}=500\text{spires}\cdot m^{-1}.$

On donne $\alpha=63.2^{\circ}$ ;

$I_{1}=2A$ et $I_{2}=1A.$

En déduire la valeur du champ résultant en $O.$

Exercice 7

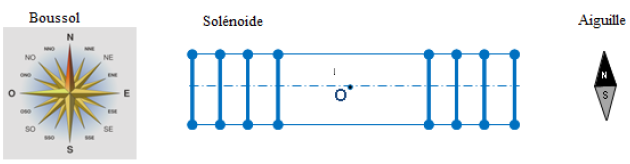
La valeur de la composante horizontale du champ géomagnétique étant trop faible pour être mesurée à l'aide d'un tesla mètre courant, on se propose de la déterminer de la manière suivante.

On place une aiguille aimantée sur pivot vertical au centre $O$ d'un solénoïde long, à spires non jointives comportant $n=200$ spires par mètre, de manière à pouvoir observer l'orientation de l'aiguille.

Le solénoïde est alors disposé horizontalement, et orienté pour que son axe soit perpendiculaire à celui de l'aiguille aimantée.

On alimente le solénoïde avec un courant d'intensité suffisante pour produire un champ magnétique en $O$ de valeur $B_{S}.$

On constate que l'axe de l'aiguille aimantée est dévié d'un angle $\alpha.$

1) Indiquer sur le schéma suivant l'orientation de la boussole placée au point $O$ en absence de courant.

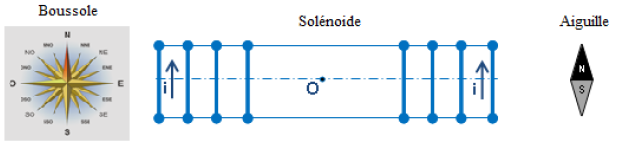
2) Représenter sans souci d'échelle sur le schéma ci-dessous, le vecteur $\overrightarrow{B_{S}}$ du champ magnétique crée par le courant électrique $i$ au centre $O$ du solénoïde.

En déduire les faces nord et sud du solénoïde.

3) Une étude expérimentale consiste à mesurer la valeur de la déviation $\alpha$ de l'aiguille aimantée placée en $O$, pour différentes valeur de l'intensité du courant $i$ qui circule dans le solénoïde.

Les résultats obtenus ont permis de tracer la courbe ci-dessous.

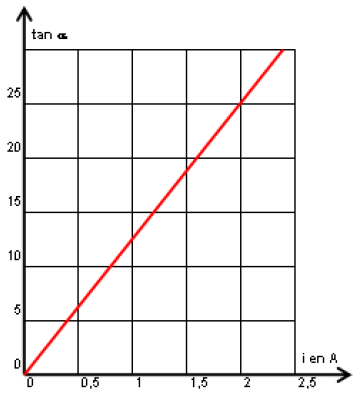
a) Déterminer l'équation numérique de la courbe $\tan\alpha=f(i).$

b) Faire un schéma sur lequel on représentera les vecteurs $B_{H}$ et $B_{S}$ (sans souci d'échelle) au point $O.$

c) Trouver une relation entre la valeur de $B_{H}$ et $B_{S}$ et $\alpha.$

4) En déduire la valeur de la composante horizontale $B_{H}$ du champ géomagnétique.

Exercice 8

On dispose d'un solénoïde de longueur $L=40\,cm$ et comportant $N=250$ spires.

On le place de telle sorte que son axe soit horizontal et perpendiculaire au plan du méridien magnétique.

Le solénoïde est parcouru par un courant électrique d'intensité constante.

Partie I

Le champ magnétique terrestre peut être négligé.

On effectue des mesures de la valeur $BS$ du champ magnétique $B_{S}$ à l'intérieur du solénoïde.

La sonde est placée sur l'axe du solénoïde à une distance $x$ de son centre $O.$

On obtient les résultats suivants :

$$\begin{array}{|c|c|c|c|c|c|c|c|} \hline x(cm)&0&4&8&11&14&17&20\\ \hline B_{S}(mT)&3.3&3.3&3.3&3.3&3.2&2.8&2.1\\ \hline \end{array}$$

1) Tracer un graphique représentant les variations de $B$ en fonction de $x$ sur toute la longueur du solénoïde.

2) Que peut-on dire du champ magnétique à l'intérieur de la bobine ?

3) Calculer l'intensité $I$ du courant qui traverse la bobine.

4) A l'aide du graphique, déterminer la longueur du solénoïde sur laquelle la valeur du champ magnétique reste supérieure à $90\%$ de sa valeur maximale.

Partie II

On fait maintenant diminuer l'intensité du courant dans les spires du solénoïde afin que la composante horizontale du champ magnétique terrestre ne soit plus négligeable.

On a $I=0.1\,A.$

On place au centre de la bobine une petite aiguille aimantée.

Celle-ci s'oriente spontanément dans une direction faisant un angle $\alpha=14.3^{\circ}$ avec l'axe du solénoïde.

1) On veut que le champ $B_{S}$ crée par la bobine soit dirigé vers la droite.

Indiquer quel doit être le sens du courant dans les spires pour que ce soit effectivement le cas.

2) Faire un schéma représentant les vecteurs champs créés par le solénoïde $B_{S}$ et par la Terre $B_{H}$, ainsi que le champ résultant $B.$

3) Calculer la nouvelle valeur de $B_{S}.$

Exercice 9

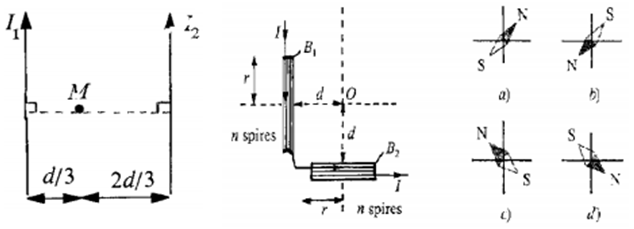
1) Calculer l'intensité du champ magnétique $\overrightarrow{B}$ créé au point $M$ par les courants $I_{1}$ et $I_{2}$ qui traversent respectivement les fils rectilignes considérés comme infiniment longs.

On donne :

$I_{1}=I_{2}=I=6.0\,A$ et $d=12\,cm$

2) On néglige le champ magnétique terrestre.

On place une petite aiguille aimantée au point $O$ ?

Quelle orientation prend-elle ?

(Choisir ci-dessous la bonne réponse en justifiant la réponse)

Deux solénoïdes $(S_{1})$ et $(S_{2})$ comportant respectivement $n_{1}=400$ spires par mètre et $n_{2}=80$ spires par mètre, sont disposés de manière à avoir le même axe ; cet axe commun étant perpendiculaire au plan du méridien magnétique terrestre (figure ci-dessous).

On place un l'aiguille aimantée mobile autour d'un axe vertical, à l'intérieur des deux solénoïdes qu'on branche en série dans un circuit électrique.

Lorsque le courant continu qui parcourt les deux solénoïdes a une intensité $I$, l'aiguille aimantée dévie de l'angle $\alpha=45^{\circ}.$

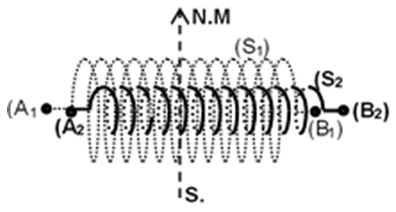
Déterminer la valeur de l'intensité $I.$

On distinguera le cas où la borne $(A_{1})$ est reliée à la borne $(B_{2})$ puis le cas où la borne $(A_{1})$ est reliée à la borne $(A_{2})$

Exercice 10

On étudie expérimentalement, à l'aide d'un teslamètre, l'intensité $B$ du champ magnétique à l'intérieur d'une bobine parcourue par un courant, en fonction de différents paramètres.

La bobine comporte $200$ spires, est longue de $40.0\,cm$, et a un diamètre de $5.0\,cm.$

I. Introduction

1. Décrire une méthode permettant de visualiser les lignes de champ de la bobine.

2. Quelles informations qualitatives peut-on tirer de l'observation des lignes de champ magnétiques quant à la nature de $Br$ à l'intérieur de la bobine ?

II. Étude de l'influence du courant circulant dans la bobine

La sonde du teslamètre est placée au centre de la bobine.

On fait varier l'intensité $I$ du courant dans la bobine et, pour chaque valeur de $I$, on note la valeur de $Br$

Le tableau ci-dessous comporte les valeurs de $I$ et $B$ obtenues :

$$\begin{array}{|c|c|c|c|c|c|c|} \hline I(A)&0&1.5&2.5&3.5&4.5&5.0\\ \hline B(10^{-5}T&0&94&153&215&280&310\\ \hline \end{array}$$

1. Faire un schéma clair et annoté du montage à réaliser pour obtenir, faire varier, et mesurer l'intensité du courant $I$ dans le circuit de la bobine.

2.1 Déterminer, à partir des données du tableau, la relation littérale entre $B$ et $I.$

2.2 Exprimer numériquement cette relation.

3.1 Donner la relation théorique entre le champ $B$ et l'intensité $I.$

3.2 En déduire la valeur expérimentale de la perméabilité magnétique du vide $\mu_{0}$

3.3 Calculer l'erreur relative avec la valeur théorique.

III. Étude de la valeur du champ magnétique le long de l'axe de la bobine

On maintient $I=4\,A$ dans la bobine.

On mesure B en divers points le long de l'axe et à la distance $x$ du centre de la bobine.

Le tableau ci-dessous donne les valeurs de $B$ en fonction de $x$ :

$$\begin{array}{|c|c|c|c|c|c|c|c|c|} \hline x(cm)&0&4&8&12&14&16&18&20\\ \hline B(mT)&2.45&2.44&2.42&3.70&2.33&2.28&2.08&1.45\\ \hline \end{array}$$

1. Tracer la courbe représentant $B$ en fonction de $x.$

Commenter l'allure de la courbe.

2. La courbe obtenue confirme-t-elle les informations obtenues à partir de l'observation des lignes de champ ?

Justifier.

3. Pour quelles valeurs de $x$ peut-on conclure que $B$ est constant à $5\%$ sur l'axe de la bobine ?

Données :

perméabilité magnétique du vide : $\mu_{0}=4\pi\cdot10^{-7}SI.$

Exercice 11

Mesure du champ magnétique terrestre

On souhaite mesurer la valeur du champ magnétique terrestre $B_{H}$, dont la valeur théorique dans le lieu de l'expérience est $B_{H}=2.0\cdot10^{-5}T.$

Pour cela, on dispose d'un solénoïde infiniment long de longueur $l=0.5\,m$, de section $S=80\,cm^{2}$, et comportant $N=50$ spires.

Les spires de ce solénoïde ne sont pas jointives, ce qui permet de voir l'intérieur du solénoïde.

On place en son centre une aiguille aimantée de façon à ce qu'elle soit perpendiculaire à la direction du champ magnétique $B_{S}$ créé par le solénoïde.

Lorsque le solénoïde est parcouru par un courant d'intensité $I$, l'aiguille s'écarte de sa position initiale d'un angle $\alpha.$

Les angles obtenus pour différentes intensités sont rassemblés dans le tableau ci-dessous :

$$\begin{array}{|c|c|c|c|c|c|} \hline I(A)&0.1&0.2&0.3&0.4&0.5\\ \hline \alpha(\text{ en }^{\circ})&33&51&63&69&73\\ \hline \end{array}$$

I. Étude préalable du protocole expérimental

1. Rappeler les propriétés du champ magnétique à l'intérieur du solénoïde.

Donner ses caractéristiques.

2.1 De quels instruments de mesure a-t-on besoin pour faire les mesures ci-dessus ?

2.2 Pourquoi a-t-on besoin de voir l'intérieur du solénoïde ?

3. Selon quelle direction (Est-Ouest ou Nord-Sud) doit être disposé le solénoïde ?

Justifier.

4.1 Calculer le champ magnétique créé par le solénoïde en son centre, si celui-ci est parcouru par une intensité $I=10\,A.$

4.2 Pour quelle raison ne peut-on pas utiliser de telles intensités pour faire les mesures d'angles ?

Combien vaudrait alors l'angle

II. Exploitation des résultats

1.1 Faire un schéma « vu de dessus » de l'aiguille au centre du solénoïde lorsqu'elle est inclinée d'un angle $\alpha.$

Dessiner les vecteurs du champ magnétique terrestre $B_{H}$ et du champ magnétique créé par le solénoïde $B_{S}$

$$\alpha=arctan\left(\dfrac{\mu_{0}n\,I}{l\,B_{H}}\right)$$

1.2 Démontrer soigneusement que l'angle $\alpha$ est donné par l'expression :

2.1 Tracer le graphique donnant la tangente de l'angle $\alpha$ $(\tan\alpha)$ en fonction de l'intensité $I.$

2.2 Calculer le coefficient directeur de la droite obtenue.

2.3 En déduire la valeur du champ magnétique terrestre $B_{H}$

2.4 Calculer l'erreur absolue et l'erreur relative de votre mesure avec la valeur théorique.

Donnée :

$\mu_{0}=4\pi\cdot10^{-7}SI.$

Exercice 12

On donne :

$B_{H}=2\cdot10^{-5}T$ On prendra $4\pi=12.5$

1) Un solénoïde $S$, de centre $O$ et de longueur $L=62.5\,cm$, comportant $N=100$ spires, est parcouru par un courant électrique d'intensité constante $I=0.2\,A.$

a) Déterminer les caractéristiques du vecteur champ magnétique créé par le courant au point $O$ centre du solénoïde $S$

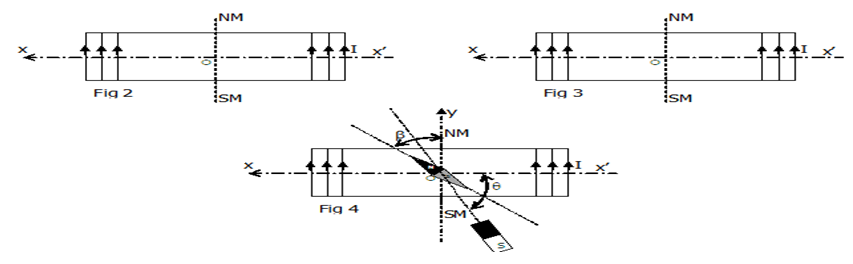
b) Sur la figure 2 (page 3 à compléter et à remettre avec la copie),

Représenter le spectre magnétique créé par le courant à l'intérieur du solénoïde S et indiquer les faces de la bobine.

2) On place au point $O$ une petite aiguille aimantée mobile autour d'un axe vertical.

Le solénoïde est placé de telle manière que son axe soit perpendiculaire au méridien magnétique.

a) Représenter sur la figure 3 (page 3 à compléter et à remettre avec la copie), les vecteurs $\overrightarrow{B}_{H}$ composante horizontale du vecteur champ magnétique terrestre et $\overrightarrow{B}_{C}$ le vecteur champ magnétique créé par le courant $I$ à l'intérieur du solénoïde en utilisant l'échelle : $1cm\ \rightarrow\ 10^{-5}T$, ainsi que la nouvelle position de l'aiguille aimantée.

b) Déterminer l'angle $\alpha$ que fait l'aiguille aimantée avec l'axe du solénoïde lorsque celle-ci prend une position d'équilibre stable.

3) On superpose avec les champs $\overrightarrow{B}_{C}$ et $\overrightarrow{B}_{H}$ un champ magnétique $\overrightarrow{B}_{a}$ créé par un aimant droit dont l'axe passe par $O$ et fait un angle $\theta=60^{\circ}$ avec l'axe du solénoïde.

Le pôle nord de l'aimant se trouve à proximité du solénoïde (figure 4, page 3 à compléter et à remettre avec la copie).

L'axe de l'aiguille aimantée s'oriente alors suivant une direction faisant un angle $\beta=45^{\circ}$ avec $\overrightarrow{B}_{H}.$

Montrer que la valeur du champ magnétique créé par l'aimant s'écrit sous la forme :

$$B_{a}=\dfrac{B_{C}-B_{H}}{\sin\theta-\cos\theta}$$

Calculer sa valeur