Relations trigonométriques dans un triangle rectangle 3e
Classe:
Troisième
I. Projection orthogonale
1) Définition - construction
Soit $(\Delta)$ une droite donnée et $A$ un point du plan n'appartenant pas à $(\Delta).$
Construisons $(\Delta')$, la droite passant par $A$ et perpendiculaire à $(\Delta).$
Et soit $H$ le point d'intersection de $(\Delta)\ $ et $\ (\Delta').$
$H$ est appelé projeté orthogonal de $A$ sur $(\Delta).$
On dit aussi que $H$ est le pied de la perpendiculaire à $(\Delta)$, issue de $A.$
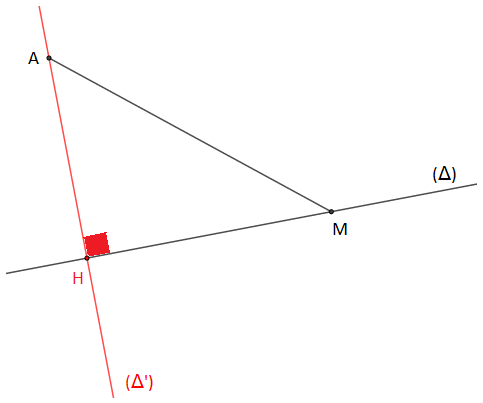
Soit $M$ un point quelconque de $(\Delta)$ tel que $M\neq H$, alors on a : $$AH<AM$$
La distance $AH$ est donc inférieure aux distances $AM$ pour tous les points $M$ appartenant à $(\Delta)$ autres que $H.$
2) Propriété
Soient $(\Delta)\ $ et $\ (\Delta')$ deux droites sécantes en $O.$
$A\ $ et $\ B$ deux points distincts de $(\Delta)$; $A'\ $ et $\ B'$ les projetés orthogonaux respectifs de $A\ $ et $\ B$ sur $(\Delta')$, alors on a : $$A'B'<AB$$
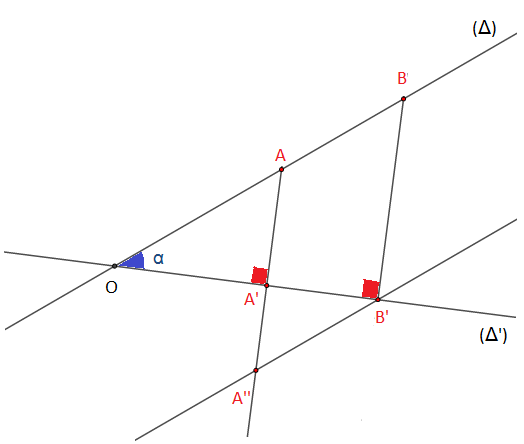
Soit $A''$ le point d'intersection de $(AA')$ à la parallèle à $(AB)$ passant par $B'.$
On aura $ABB'B''$ un parallélogramme, alors $AB=A''B'.$
Et comme $A'B'<A''B'$, donc $\boxed{A'B'<AB}$
3) Rapport de projection orthogonale
a) Activité
Soient $[Ox)\ $ et $\ [Oy)$ deux demi-droites de même origine $O$ et de supports non parallèles tels que $\widehat{xOy}=60^{\circ}.$
Soient $A\;,\ B\ $ et $\ C$ trois points de $[Oy)$ tels que $OA=5\;cm\;,\ OB=8\;cm\ $ et $\ OC=10\;cm.$
$A'\;,\ B'\ $ et $\ C'$ sont les projetés orthogonaux respectivement de $A\;,\ B\ $ et $\ C$ sur $[Ox).$
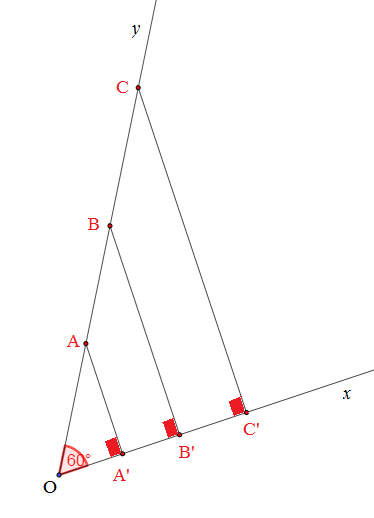
On a : $OA'=2.5\;cm\;,\ OB'=4\;cm\ $ et $\ OC'=5\;cm.$
Alors, $\dfrac{OA'}{OA}=\dfrac{2.5}{5}=\dfrac{1}{2}\;,\ \dfrac{OB'}{OB}=\dfrac{4}{8}=\dfrac{1}{2}$ et $\dfrac{OC'}{OC}=\dfrac{5}{10}=\dfrac{1}{2}.$
$\dfrac{A'B'}{AB}=\dfrac{1.5}{3}=\dfrac{1}{2}\ $ et $\ \dfrac{A'C'}{AC}=\dfrac{2.5}{5}=\dfrac{1}{2}$
Donc, $\dfrac{OA'}{OA}=\dfrac{OB'}{OB}=\dfrac{OC'}{OC}=\dfrac{A'B'}{AB}=\dfrac{A'C'}{AC}=\dfrac{1}{2}$
b) Définition
Soient $(\Delta)\ $ et $\ (\Delta')$ deux droites non parallèles, $A\ $ et $\ B$ deux points de $(\Delta)$, $A'\;,\ B'$ leur projetés orthogonaux respectifs sur la droite $(\Delta').$
On appelle rapport de projeté orthogonal sur la droite $(\Delta')$ à la droite $(\Delta)$ le rapport $\dfrac{A'B'}{AB}.$
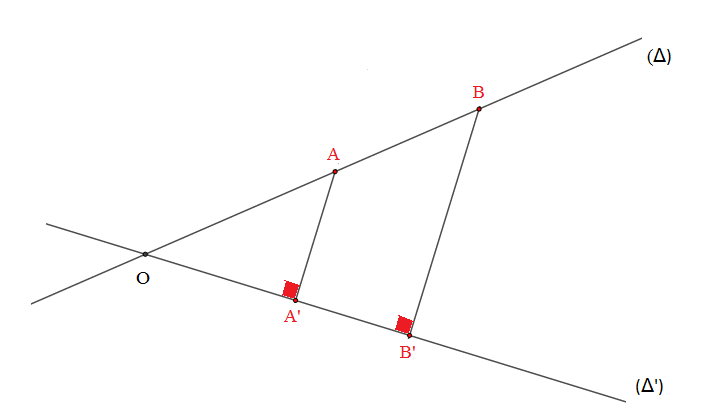
Si on désigne par $r$ ce rapport de projection orthogonale de $(\Delta)$ sur $(\Delta').$
On écrira : $r=\dfrac{OA'}{OA}=\dfrac{OB'}{OB}=\dfrac{A'B'}{AB}$
Remarque :
Le rapport de projection orthogonale de la droite $(\Delta)$ sur la droite $(\Delta')$ est indépendant de la position de $A\ $ et $\ B$ sur $(\Delta)$ mais dépend uniquement de l'angle formé par les deux droites.
c) Propriétés :
Le rapport de projection orthogonale de la droite $(\Delta)$ sur la droite $(\Delta')$ est égal au rapport de projection de la droite $(\Delta')$ sur la droite $(\Delta).$
On dira que le rapport de projection orthogonale est symétrique.
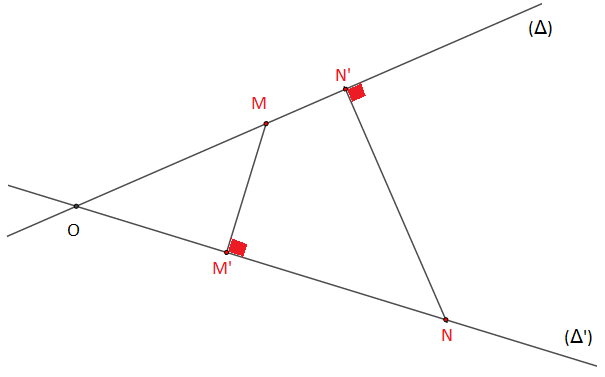
$r=\dfrac{OM'}{OM}=\dfrac{ON'}{ON}$
d) Valeurs du rapport
Soit $r$ le rapport de projection orthogonale des droites $(\Delta)\ $ et $\ (\Delta').$
$\centerdot\ \ $ $(\Delta)\ $ et $\ (\Delta')$ sécantes en $O$
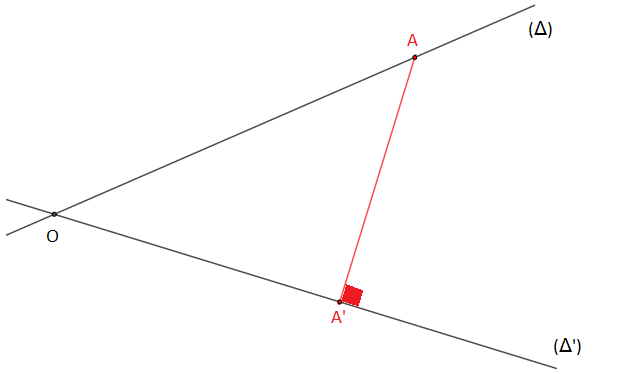
On a : $OA'<OA$
Alors, $\dfrac{OA'}{OA}<\dfrac{OA}{OA}$
Donc, $r<1$
Remarque :
Si $(\Delta)\perp(\Delta')$ alors, $r=0$
D'où, $0\leq r<1$
$(\Delta)\ $ et $\ (\Delta')$ sont confondues
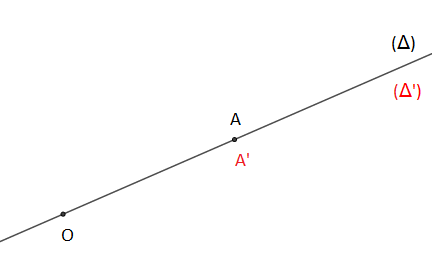
On a : $r=\dfrac{OA'}{OA}=\dfrac{OA}{OA}=1$
II. Relations trigonométriques dans un triangle rectangle
Rappel
Soit $ABC$ un triangle rectangle en $A$, $x\ $ et $\ y$ les angles respectifs aux sommets $B\ $ et $\ C$
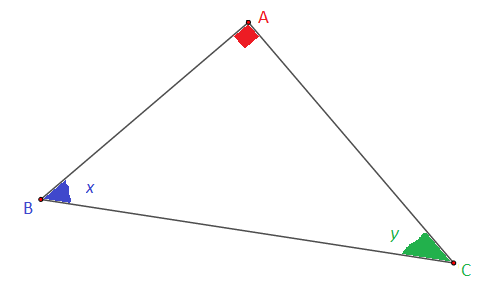
$\centerdot\ \ $ On a $x<90^{\circ}\ $ et $\ y<90^{\circ}\ $ et $\ x+y=90^{\circ}.$
Dans un triangle rectangle, on a deux angles aigus complémentaires.
$\centerdot\ \ $ Si $ABC$ un triangle et $\widehat{ABC}+\widehat{ACB}=90^{\circ}$ alors, $ABC$ est un triangle rectangle en $A.$
Si dans un triangle, on a deux angles complémentaires alors, c'est un triangle rectangle.
$\centerdot\ \ $ Si $ABC$ un triangle rectangle en $A$, alors $BC>AB\ $ et $\ BC>AC.$
Dans un triangle rectangle le côté opposé à l'angle droit est le plus grand côté et il est appelé l'hypoténuse.
$\centerdot\ \ $ Si $ABC$ un triangle rectangle en $A$ alors, $BC^{2}=AB^{2}+AC^{2}.$
Dans un triangle rectangle, le carré de l'hypoténuse est égal à la mesure des carrés des deux autres côtés (théorème de Pythagore)
$\centerdot\ \ $ Si $ABC$ un triangle rectangle et $BC^{2}=AB^{2}+AC^{2}$ alors, $ABC$ est rectangle en $A.$
Si dans un triangle, le carré d'un côté est égal à la somme des carrés des deux autres, alors c'est un triangle rectangle.
$\centerdot\ \ $ On appelle côté opposé à un angle aigu, le côté qui fait face à l'angle aigu dans le triangle rectangle.
$[AB]\ $ et $\ [AC]$ sont appelés côtés opposés aux angles respectifs $y\ $ et $\ x.$
$\centerdot\ \ $ On appelle côté adjacent à un angle aigu dans un triangle rectangle, le côté qui porte l'angle dans le triangle autre que l'hypoténuse.
$[AB]\ $ et $\ [AC]$ sont appelés côtés adjacents aux angles respectifs $x\ $ et $\ y.$
III. Cosinus d'un angle aigu
On appelle cosinus d'un angle aigu $x$, noté $\cos x$, le rapport de la longueur du côté adjacent à l'ange $x$ sur la longueur de l'hypoténuse.
On écrira : $$\boxed{\cos x=\dfrac{\text{côté adjacent à }x}{\text{hypoténuse}}}$$
Ainsi, $$\cos x=\dfrac{AB}{BC}\quad\text{ et }\quad\cos y=\dfrac{AC}{BC}$$
Exemple 1 :
Soit $ABC$ un triangle rectangle en $A$ tel que $AB=4\;cm\ $ et $\ BC=5\;cm$
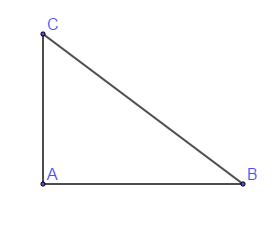
1) Calcul de $AC$
On a $ABC$ triangle rectangle en $A$ alors, $AB^{2}+AC^{2}=BC^{2}$
Donc, $AC^{2}=BC^{2}-AB^{2}$
Ainsi, $AC=\sqrt{BC^{2}-AB^{2}}$
D'où, $AC=\sqrt{25-16}=3\;cm$
2) Calcul de $\cos\widehat{ABC}\ $ et $\ \cos\widehat{ACB}$
On a $ABC$ triangle rectangle en $A$, alors $\cos\widehat{ABC}=\dfrac{AB}{BC}\ $ et $\ \cos\widehat{ACB}=\dfrac{AC}{BC}$
Donc, $\cos\widehat{ABC}=\dfrac{4}{5}\ $ et $\ \cos\widehat{ACB}=\dfrac{3}{5}$
D'où, $\cos\widehat{ABC}=0.8\ $ et $\ \cos\widehat{ACB}=0.6$
Exemple 2 :
On considère la figure suivante
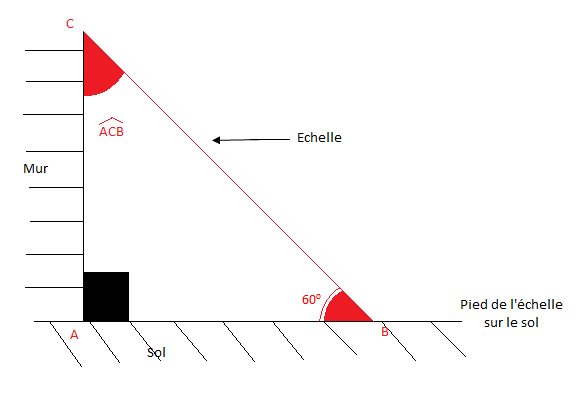
On donne $AB=3\;m\ $ et $\ \cos 60^{\circ}=\dfrac{1}{2}$
1) Calcul de la longueur de l'échelle : $BC$
On a $ABC$ triangle rectangle en $A$, alors $\cos\widehat{ABC}=\dfrac{AB}{BC}$
Donc, $BC=\dfrac{AB}{\cos\widehat{ABC}}$
Ainsi, $BC=\dfrac{3}{\cos 60^{\circ}}=\dfrac{3}{\dfrac{1}{2}}$
D'où, $BC=3\times\dfrac{2}{1}=6\;m$
2) Calcul de $AC$ (hauteur du pied de l'échelle sur le mur au sol)
On a $ABC$ triangle rectangle en $A$, alors $AB^{2}+AC^{2}=BC^{2}$
Donc, $AC^{2}=BC^{2}-AB^{2}$
Ainsi, $AC=\sqrt{BC^{2}-AB^{2}}$
D'où, $AC=\sqrt{36-9}=\sqrt{27}=3\sqrt{3}\;m$
3) Mesure de $\widehat{ACB}$
On a $ABC$ un triangle rectangle en $A$
Alors, $\widehat{ABC}+\widehat{ACB}=90^{\circ}$
Donc, $\widehat{ACB}=90^{\circ}-\widehat{ABC}$
Ainsi, $\widehat{ACB}=90^{\circ}-60^{\circ}$
D'où, $\widehat{ACB}=30^{\circ}$
4) Calcul de $\cos\widehat{ACB}$
On a $ABC$ triangle rectangle en $A$, alors $\cos\widehat{ACB}=\dfrac{AC}{BC}$
Donc, $\cos\widehat{ACB}=\dfrac{3\sqrt{3}}{6}$
D'où, $\cos\widehat{ACB}=\dfrac{\sqrt{3}}{2}$
IV. Sinus d'un angle aigu
On appelle sinus d'un angle aigu $x$, noté $\sin x$, le rapport de la longueur du côté opposé à l'ange $x$ sur la longueur de l'hypoténuse.
On écrira : $$\boxed{\sin x=\dfrac{\text{côté opposé à }x}{\text{hypoténuse}}}$$
Ainsi, $$\sin x=\dfrac{AC}{BC}\quad\text{ et }\quad\sin y=\dfrac{AB}{BC}$$
V. Sinus et cosinus d'angles complémentaires
On avait $$\sin x=\dfrac{AC}{BC}\quad\text{ et }\quad\cos x=\dfrac{AB}{BC}$$
$$\sin y=\dfrac{AB}{BC}\quad\text{ et }\quad\cos y=\dfrac{AC}{BC}$$
Alors, $\sin x=\cos y$ et $\sin y=\cos x$
Si deux angles sont complémentaires, le sinus de l'un est égal au cosinus de l'autre.
$$\boxed{\text{Si }x+y=90^{\circ},\;\text{ alors }\cos x=\sin y\;\text{ et }\;\cos y=\sin x}$$
VI. Relation entre sinus et cosinus d'un angle aigu
On a $ABC$ un triangle rectangle en $A$
Alors, $AB^{2}+AC^{2}=BC^{2}$
Donc, $\dfrac{AB^{2}}{BC^{2}}+\dfrac{AC^{2}}{BC^{2}}=\dfrac{BC^{2}}{BC^{2}}$
c'est à dire $\left(\dfrac{AB}{BC}\right)^{2}+\left(\dfrac{AC}{BC}\right)^{2}=1$
Ainsi, $(\cos x)^{2}+(\sin x)^{2}=1$
en posant $(\cos x)^{2}=\cos^{2} x$ et $(\sin x)^{2}=\sin^{2} x$
on obtient $$\boxed{\cos^{2} x+\sin^{2} x=1}$$
Exemple :
Soit $ABC$ un triangle rectangle en $A$ tel que $AB=4\;cm$
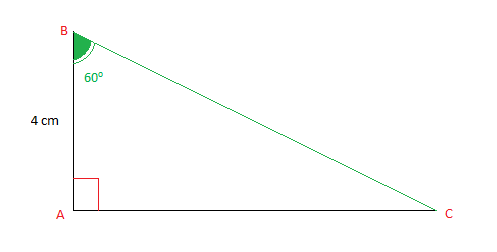
l'angle $\widehat{ABC}=60^{\circ}$ et $\sin 60^{\circ}=\dfrac{\sqrt{3}}{2}$
Calculons $BC$ et $AC$
On a : $\cos^{2}\widehat{ABC}+\sin^{2}\widehat{ABC}=1$
Alors, $\cos^{2}\widehat{ABC}=1-\sin^{2}\widehat{ABC}$
Donc, $\cos\widehat{ABC}=\sqrt{1-\sin^{2}\widehat{ABC}}$
Ainsi, $\cos\widehat{ABC}=\sqrt{1-\left(\dfrac{\sqrt{3}}{2}\right)^{2}}=\sqrt{1-\dfrac{3}{4}}=\sqrt{\dfrac{1}{4}}=\dfrac{1}{2}$
Par suite, $\cos\widehat{ABC}=\dfrac{AB}{BC}$
c'est à dire $BC=\dfrac{AB}{\cos\widehat{ABC}}=\dfrac{4}{\dfrac{1}{2}}=8\;cm$
et $\sin\widehat{ABC}=\dfrac{AC}{BC}$
Ce qui donne : $AC=BC\times\sin\widehat{ABC}$
Donc, $AC=8\times\dfrac{\sqrt{3}}{2}=4\sqrt{3}\;cm$
VII. Tangente d'un angle aigu
On appelle tangente d'un angle aigu $x$, notée $\tan x$ ou $tg\;x$, le rapport du sinus de l'angle $x$ par son cosinus.
On écrira : $$\boxed{\tan x=\dfrac{\sin x}{\cos x}\quad\text{et}\quad\tan y=\dfrac{\sin y}{\cos y}}$$
Autres formulations :
On a : $\tan x=\dfrac{\sin x}{\cos x}$
Or, $\sin x=\dfrac{AC}{BC}$ et $\cos x=\dfrac{AB}{BC}$
Alors, $\tan x=\dfrac{\dfrac{AC}{BC}}{\dfrac{AB}{BC}}$
Donc, $\tan x=\dfrac{AC}{BC}\times\dfrac{BC}{AB}$
D'où, $\tan x=\dfrac{AC}{AB}$
La tangente d'un angle aigu dans un triangle rectangle se définit comme étant le rapport de la longueur du côté opposé à l'angle par son côté adjacent.
On écrira : $$\boxed{\tan x=\dfrac{\text{côté opposé à }x}{\text{côté adjacent à }x}}$$
Ainsi, $$\tan x=\dfrac{AC}{AB}\quad\text{ et }\quad\tan y=\dfrac{AB}{AC}$$
Remarque :
Si deux angles complémentaires, la tangente de l'une est égale à l'inverse de la tangente de l'autre.
$$\boxed{\text{Si }x+y=90^{\circ},\;\text{ alors }\tan x=\dfrac{1}{\tan y}}$$
VIII. Sinus, cosinus et tangente d'angles remarquables
$$\begin{array}{|c|c|c|c|c|c|}\hline\text{Angle }x & 0^{\circ} & 30^{\circ} & 45^{\circ} & 60^{\circ} & 90^{\circ} \\ \hline\text{Sinus} & 0 & \frac{1}{2} & \frac{\sqrt{2}}{2} & \frac{\sqrt{3}}{2} & 1 \\ \hline\text{Cosinus} & 1 & \frac{\sqrt{3}}{2} & \frac{\sqrt{2}}{2} & \frac{1}{2} & 0 \\ \hline\text{Tangente} & 0 & \frac{\sqrt{3}}{3} & 1 & \sqrt{3} &\times \\ \hline\end{array}$$
XI. Applications : Relations métriques dans un triangle rectangle
Soit $ABC$ un triangle rectangle en $A$, $H$ le projeté orthogonal de $A$ sur $(BC).$
On donne $AB=4\;cm\;,\ AC=3\;cm\ $ et $\ BC=5\;cm$
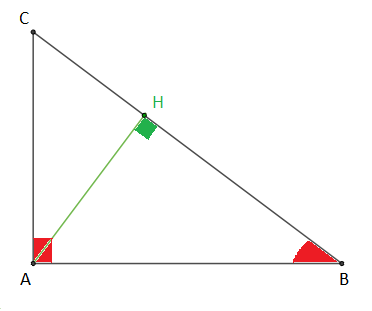
$\centerdot\ \ $ Exprimons $\cos\widehat{ABC}$ de deux manières
On a $ABC$ un triangle rectangle en $A$, alors $\cos\widehat{ABC}=\dfrac{AB}{BC}.$
De même on a $ABH$ un triangle rectangle en $H$, alors $\cos\widehat{ABH}=\dfrac{BH}{AB}$
Or, $\widehat{ABH}=\widehat{ABC}$
Donc, $\cos\widehat{ABC}=\dfrac{BH}{AB}$
$\centerdot\ \ $ Relations entre $AB\;,\ BC\ $ et $\ BH$
On a : $\cos\widehat{ABC}=\dfrac{AB}{BC}\ $ et $\ \cos\widehat{ABC}=\dfrac{BH}{AB}$
Alors, $\dfrac{AB}{BC}=\dfrac{BH}{AB}$
Donc, $$\boxed{AB^{2}=BH\times BC\qquad 1^{e}\;\text{relation métrique}}$$
Valeur de $BH$
On a : $AB^{2}=BH\times BC$
Alors, $BH=\dfrac{AB^{2}}{BC}$
Donc, $BH=\dfrac{16}{5}=3.2\;cm$
$\centerdot\ \ $ Relations entre $AC\;,\ BC\ $ et $\ CH$
On a $ABC$ un triangle rectangle en $A$
Alors, $\cos\widehat{ACB}=\dfrac{AC}{BC}$
De même on a $ACH$ un triangle rectangle en $H$, alors $\cos\widehat{ACH}=\dfrac{CH}{AC}$
Or, $\widehat{ACH}=\widehat{ACB}$
Donc, $\cos\widehat{ACB}=\dfrac{CH}{AC}$
Par suite, $\dfrac{AC}{BC}=\dfrac{CH}{AC}$
D'où, $$\boxed{AC^{2}=CH\times BC\qquad 2^{e}\;\text{relation métrique}}$$
Valeur de $CH$
On aura $CH=\dfrac{AC^{2}}{BC}$
Donc, $BH=\dfrac{9}{5}=1.8\;cm$
$\centerdot\ \ $ Relations entre $AH\;,\ BH\ $ et $\ CH$
On a $ABH$ un triangle rectangle en $H$, alors $\tan\widehat{ABH}=\dfrac{AH}{BH}$
Or, $\widehat{ABH}=\widehat{ABC}$
Donc, $\tan\widehat{ABC}=\dfrac{AH}{BH}$
De même on a $ACH$ un triangle rectangle en $H$, alors $\tan\widehat{ACH}=\dfrac{AH}{CH}$
Or, $\widehat{ACH}=\widehat{ACB}$
Donc, $\tan\widehat{ACB}=\dfrac{AH}{CH}$
et comme $\widehat{ABC}+\widehat{ACB}=90^{\circ}$, on aura $\tan\widehat{ABC}=\dfrac{1}{\tan\widehat{ACB}}$
Par suite, $\dfrac{AH}{BH}=\dfrac{1}{\dfrac{AH}{CH}}$
Ainsi, $\dfrac{AH}{BH}=\dfrac{CH}{AH}$
D'où, $$\boxed{AH^{2}=BH\times CH\qquad 3^{e}\;\text{relation métrique}}$$
Valeur de $AH$
On aura $AH=\sqrt{BH\times CH}$
Donc, $BH=\sqrt{\dfrac{16}{5}\times\dfrac{9}{5}}=\dfrac{12}{5}=2.4\;cm$
Auteur:
Abdoulaye Ba

Commentaires
Anonyme (non vérifié)
lun, 01/21/2019 - 21:01
Permalien
Bien
Kia (non vérifié)
mar, 01/14/2020 - 23:10
Permalien
Je vaudrait savoir plus sur la relation metrique
Kia (non vérifié)
mar, 01/14/2020 - 23:16
Permalien
Vaudrai
Anonyme (non vérifié)
sam, 05/23/2020 - 18:41
Permalien
VRAIMENT TRES INTERESSANT
Anonyme (non vérifié)
sam, 05/23/2020 - 18:41
Permalien
VRAIMENT TRÈS INTÉRESSANT
Oury diallo (non vérifié)
jeu, 02/25/2021 - 23:20
Permalien
Réussir mon bfem
Mamadou Diallo (non vérifié)
jeu, 01/19/2023 - 21:06
Permalien
Bonsoir les cours sont
Mamadou Diallo (non vérifié)
jeu, 01/19/2023 - 21:07
Permalien
Intéressant
Ajouter un commentaire