Vous êtes ici

Solution des exercices : Théorème de Thalès - 3e

Classe:

Troisième

Exercice 1

Calculons

$x$ dans les cas suivants :

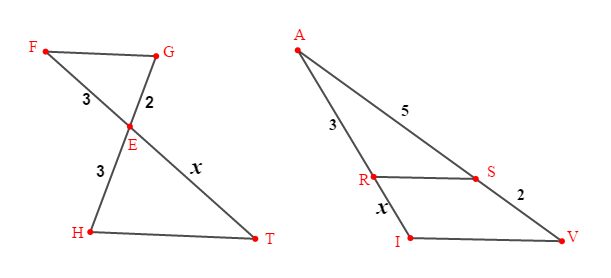
Dans le premier cas, les droites

$(FT)\$ et

$\ (HG)$ sécantes en

$E$ sont coupées par deux droites parallèles

$(FG)\$ et

$\ (HT)$ donc, d'après le théorème de Thalès on a :

$\dfrac{EF}{ET}=\dfrac{EG}{EH}=\dfrac{FG}{HT}$

Par suite,

$\begin{array}{rcl}\dfrac{EF}{ET}=\dfrac{EG}{EH}&\Rightarrow&\dfrac{3}{x}=\dfrac{2}{3}\\ \\&\Rightarrow&2x=9\\ \\&\Rightarrow&x=\dfrac{9}{2}\end{array}$

D'où,

$\boxed{x=\dfrac{9}{2}}$

Dans le deuxième cas, les droites

$(AI)\$ et

$\ (AV)$ sécantes en

$A$ sont coupées par deux droites parallèles

$(RS)\$ et

$\ (IV)$ donc, les triangles

$ARS\$ et

$\ AIV$ sont en position de Thalès.

Ainsi, en appliquant le théorème de Thalès, on obtient :

$\dfrac{AR}{AI}=\dfrac{AS}{AV}=\dfrac{RS}{IV}$

Par suite,

$\begin{array}{rcl}\dfrac{AR}{AI}=\dfrac{AS}{AV}&\Rightarrow&\dfrac{3}{3+x}=\dfrac{5}{7}\\ \\&\Rightarrow&5(3+x)=21\\ \\&\Rightarrow&5x=21-15\\ \\&\Rightarrow&x=\dfrac{6}{5}\end{array}$

D'où,

$\boxed{x=\dfrac{6}{5}}$

Exercice 2

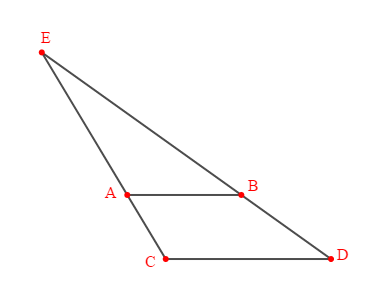
Dans chacun des cas suivants,

$E\;,\ A\;,\ C$ sont trois points alignés d'une part, et

$E\;,\ B\;,\ D$ trois points alignés d'autre part, dans le même ordre.

Alors, d'après la réciproque du théorème de Thalès, si on a :

$\dfrac{EA}{EC}=\dfrac{EB}{ED}$ , on dira que les droites

$(AB)\$ et

$\ (CD)$ sont parallèles.

Dans le 1er cas on donne :

$EA=\dfrac{1}{2}\;;\ EC=\dfrac{2}{3}\;;\ EB=3\;;\ ED=4$

Calculons alors les rapports

$\dfrac{EA}{EC}\;,\ \dfrac{EB}{ED}$

On a :

$\dfrac{EA}{EC}=\dfrac{\dfrac{1}{2}}{\dfrac{2}{3}}=\dfrac{3}{4}\;,\quad\text{et }\ \dfrac{EB}{ED}=\dfrac{3}{4}$

Par suite,

$\dfrac{EA}{EC}=\dfrac{EB}{ED}$

Ainsi, les droites

$(AB)\$ et

$\ (CD)$ sont parallèles.

Dans le 2ème cas on donne :

$EA=2\;;\ EC=3.2\;;\ EB=4\;;\ ED=6$

Le calcul des rapports

$\dfrac{EA}{EC}\;,\ \dfrac{EB}{ED}$ donne :

$\dfrac{EA}{EC}=\dfrac{2}{3.2}=\dfrac{2}{3.2}\;,\quad\text{et }\ \dfrac{EB}{ED}=\dfrac{4}{6}=\dfrac{2}{3}$

Ce qui montre que les rapports

$\dfrac{EA}{EC}\$ et

$\ \dfrac{EB}{ED}$ sont différents ;

$\ \left(\dfrac{2}{3.2}\neq\dfrac{2}{3}\right)$

Or, pour que les droites

$(AB)\$ et

$\ (CD)$ soient parallèles, il faut avoir

$\dfrac{EA}{EC}=\dfrac{EB}{ED}$ , d'après la réciproque du théorème de Thalès.

Par conséquent, les droites

$(AB)\$ et

$\ (CD)$ ne sont pas parallèles, pour ce deuxième cas.

Exercice 3

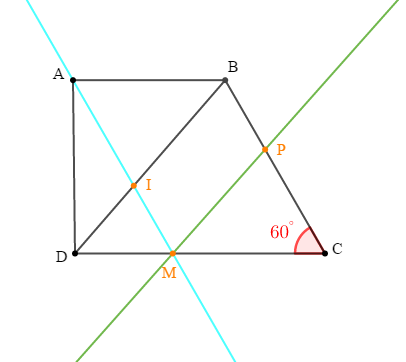
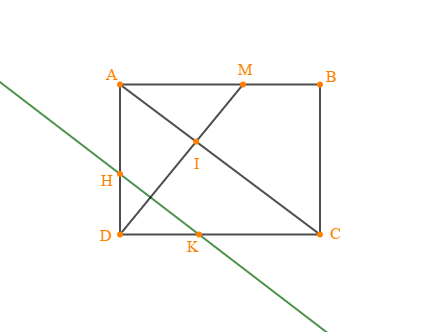
$ABCD$ est un trapèze de bases

$(AB)\$ et

$\ (DC)$ tel que :

$AB=3\;cm\;;\ BC=4\;cm\;;\ DC=5\;cm\$ et

$\ \widehat{BCD}=60^{\circ}$

La parallèle à

$(BC)$ passant par

$A$ coupe

$(BD)$ en

$I$ et

$(DC)$ en

$M.$

1) Faisons la figure.

2) Nature du quadrilatère

$ABCM$

En effet, la parallèle à

$(BC)$ passant par

$A$ coupe

$(DC)$ en

$M.$

Donc, les droites

$(AM)\$ et

$\ (BC)$ sont parallèles.

De plus,

$ABCD$ est un trapèze dont les bases

$(AB)\$ et

$\ (DC)$ sont parallèles.

Par suite,

$ABCM$ est un quadrilatère dont les côtés sont parallèles deux à deux.

Par conséquent,

$ABCM$ est un parallélogramme.

Déduisons

$MC$

$ABCM$ étant un parallélogramme alors,

$MC=AB\$ or,

$\ AB=3\;cm$

Donc,

$\boxed{MC=3\;cm}$

Calculons

$AI$

On a :

$(IM)$ parallèle à

$(BC)$ donc, les triangles

$DIM\$ et

$\ DBC$ sont en position de Thalès.

Ainsi, d'après le théorème de Thalès, on aura :

$\dfrac{DM}{DC}=\dfrac{DI}{DB}=\dfrac{MI}{BC}$

Par suite,

$\begin{array}{rcl}\dfrac{MI}{BC}=\dfrac{DM}{DC}&\Rightarrow&\dfrac{MI}{BC}=\dfrac{DC-MC}{DC}\quad\text{car }\ DM=DC-MC\\ \\&\Rightarrow&\dfrac{MI}{4}=\dfrac{5-3}{5}\\ \\&\Rightarrow&5\times MI=2\times 4\\ \\&\Rightarrow&MI=\dfrac{8}{5}\\ \\&\Rightarrow&MI=1.6\end{array}$

Ainsi,

$\boxed{MI=1.6\;cm}$

Par ailleurs,

$AI=AM-MI$

Mais comme

$ABCM$ est un parallélogramme alors,

$AM=BC=4\;cm$

Par conséquent,

$\begin{array}{rcl} AI=BC-MI&=&4-1.6\\ \\&=&2.4\end{array}$

D'où,

$\boxed{AI=2.4\;cm}$

3) Soit

$P$ un point de

$[BC]$ tel que

$PC=2.4$

Montrons que les droites

$(MN)\$ et

$\ (DB)$ sont parallèles.

Soit

$C\;,\ P\;,\ B$ trois points alignés d'une part, et

$C\;,\ M\;,\ D$ trois points alignés d'autre part, dans le même ordre.

On a :

$\dfrac{CM}{CD}=\dfrac{3}{5}=0.6\quad\text{et}\quad\dfrac{CP}{CB}=\dfrac{2.4}{4}=0.6$

Ce qui montre que :

$\dfrac{CM}{CD}=\dfrac{CP}{CB}$

D'où, les droites

$(MP)\$ et

$\ (DB)$ sont parallèles, d'après la réciproque du théorème de Thalès.

Exercice 4

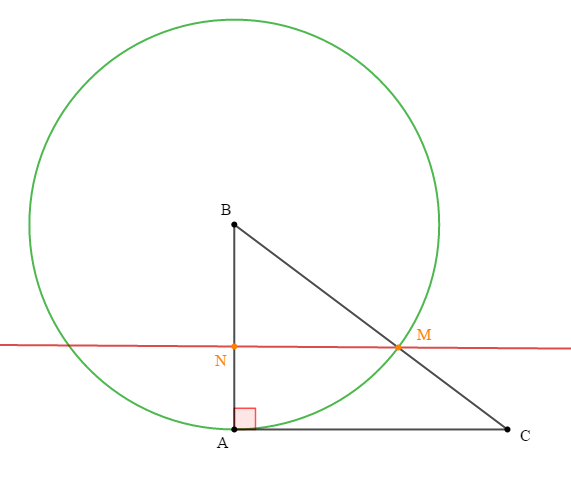
On considère le triangle

$ABC$ rectangle en

$A$ tel que

$AB=6\$ et

$\ AC=8.$

Le cercle de centre

$B$ et de rayon 6 coupe

$[BC]$ en

$M.$

Soit

$N$ un point du segment

$[AB]$ tel que

$AN=2.4$

1) Calculons

$BC$

Le triangle étant rectangle en

$A$ , on utilise le théorème de Pythagore pour calculer

$BC.$

On a :

$\begin{array}{rcl} BC^{2}=AB^{2}+AC^{2}&\Rightarrow&BC=\sqrt{AB^{2}+AC^{2}}\\\\&\Rightarrow&BC=\sqrt{36+64}\\\\&\Rightarrow&BC=\sqrt{100}\\\\&\Rightarrow&BC=10\end{array}$

D'où,

$\boxed{BC=10}$

2) Démontrons que les droites

$(MN)\$ et

$\ (AC)$ sont parallèles

Considérons

$B\;,\ N\;,\ A$ trois points alignés d'une part, et

$B\;,\ M\;,\ C$ trois points alignés d'autre part, dans le même ordre.

Calculons alors les rapports

$\dfrac{BN}{AB}\quad\text{et}\quad\dfrac{BM}{BC}$

On a :

$\begin{array}{rcl}\dfrac{BN}{AB}&=&\dfrac{AB-AN}{AB}\quad\text{car, }\ BN=AB-AN\\ \\&=&\dfrac{6-2.4}{6}\\ \\&=&\dfrac{3.6}{6}\\ \\&=&0.6\end{array}$

D'où,

$\dfrac{BN}{AB}=0.6$

Aussi, on sait que

$M\in\;\mathcal{C}(B\;,\ 6)$ donc,

$BM=6$

Par suite,

$\dfrac{BM}{BC}=\dfrac{6}{10}=0.6$

Ce qui montre alors :

$\dfrac{BN}{BA}=\dfrac{BM}{BC}$

Par conséquent, la réciproque du théorème de Thalès permet de conclure que les droites

$(MN)\$ et

$\ (AC)$ sont parallèles.

Calculons

$MN$

Les droites

$(MN)\$ et

$\ (AC)$ étant parallèles alors, les triangles

$BNM\$ et

$\ BAC$ sont en position de Thalès.

Ainsi, d'après le théorème de Thalès, on obtient :

$\dfrac{BN}{BA}=\dfrac{BM}{BC}=\dfrac{MN}{AC}$

Par suite,

$\begin{array}{rcl}\dfrac{MN}{AC}=\dfrac{BM}{BC}&\Rightarrow&\dfrac{MN}{8}=\dfrac{6}{10}\\ \\&\Rightarrow&10\times MN=6\times 8\\ \\&\Rightarrow&MN=\dfrac{48}{10}\\ \\&\Rightarrow&MN=4.8\end{array}$

D'où,

$\boxed{MN=4.8}$

Exercice 5

Considérons un rectangle

$ABCD$ tel que

$AB=4\;cm\;,\ BC=3\;cm.$

$M$ est un point de

$[AB]$ tel que

$AM=2.5\;cm\$ et soit

$\ (AC)$ et

$\ (DM)$ deux droites qui se coupent en

$I.$

Soit

$K$ un point de

$[CD]$ tel que

$DK=1.6\;cm\$ et

$\ H$ un point de

$[DA]$ tel que

$AH=1.8\;cm$

1) Calculons

$AC$

Comme

$ABCD$ est un rectangle alors, le triangle

$ABC$ est rectangle en

$B.$

Donc, pour calculer

$AC$ on applique le théorème de Pythagore :

$AC^{2}=AB^{2}+BC^{2}$

Alors, on a :

$\begin{array}{rcl} AC^{2}=AB^{2}+BC^{2}&\Rightarrow&AC=\sqrt{AB^{2}+BC^{2}}\\\\&\Rightarrow&AC=\sqrt{16+9}\\\\&\Rightarrow&AC=\sqrt{25}\\\\&\Rightarrow&AC=5\end{array}$

D'où,

$\boxed{AC=5\;cm}$

Calculons

$AI$

$ABCD$ étant un rectangle donc,

$AB=DC$ et les droites

$(AB)\$ et

$\ (DC)$ sont parallèles.

Comme

$(AB)\$ et

$\ (AM)$ sont confondues, cela revient donc à dire que les droites

$(AM)\$ et

$\ (DC)$ sont parallèles.

Par suite, les droites

$(AC)\$ et

$\ (DM)$ sécantes en

$I$ étant coupées par deux droites parallèles

$(AM)\$ et

$\ (DC)$ alors, en appliquant le théorème de Thalès, on obtient :

$\dfrac{IM}{ID}=\dfrac{AI}{IC}=\dfrac{AM}{DC}$

Ainsi,

$\begin{array}{rcl}\dfrac{AI}{IC}=\dfrac{AM}{DC}&\Rightarrow&\dfrac{AI}{IC}=\dfrac{2.5}{4}\\ \\&\Rightarrow&4\times AI=2.5\times IC\quad\text{or, }\ IC=AC-AI\\ \\&\Rightarrow&4\times AI=2.5(AC-AI)\quad\text{or, }\ AC=5\;cm\\ \\&\Rightarrow&4\times AI=2.5\times(5-AI)\\ \\&\Rightarrow&4\times AI+2.5\times AI=12.5\\ \\&\Rightarrow&6.5\times AI=12.5\\ \\&\Rightarrow&AI=\dfrac{12.5}{6.5}\\ \\&\Rightarrow&AI=1.9\end{array}$

Donc,

$\boxed{AI=1.9\;cm}$

2) Démontrons que les droites

$(HK)\$ et

$\ (AC)$ sont parallèles.

Considérons

$D\;,\ H\;,\ A$ trois points alignés d'une part, et

$D\;,\ K\;,\ C$ trois points alignés d'autre part, dans le même ordre.

Calculons les rapports

$\dfrac{DH}{DA}\quad\text{et}\quad\dfrac{DK}{DC}$

On a :

$\begin{array}{rcl}\dfrac{DH}{DA}&=&\dfrac{DA-AH}{DA}\quad\text{car, }\ DH=DA-AH\\ \\&=&\dfrac{3-1.8}{3}\\ \\&=&\dfrac{1.2}{3}\\ \\&=&0.4\end{array}$

D'où,

$\dfrac{DH}{DA}=0.4$

Aussi,

$\dfrac{DK}{DC}=\dfrac{1.6}{4}=0.4$

On constate alors :

$\dfrac{DH}{DA}=\dfrac{DK}{DC}$

Par conséquent, la réciproque du théorème de Thalès permet de conclure que les droites

$(HK)\$ et

$\ (AC)$ sont parallèles.

Exercice 6

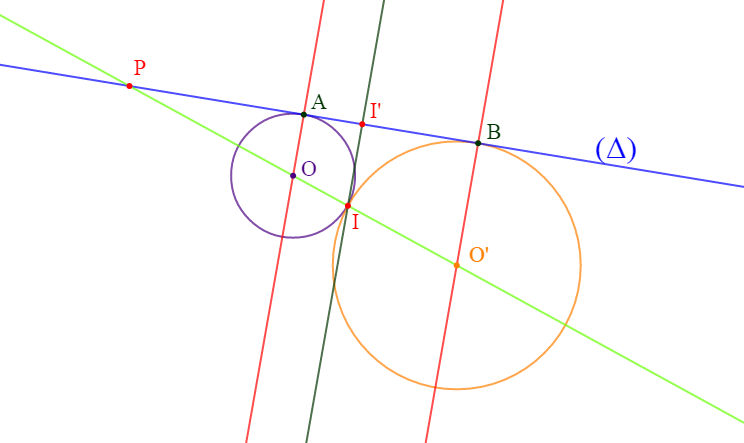
On considère deux cercles

$\mathcal{C}(O\;;\ 1.5)\$ et

$\ \mathcal{C}'(O'\;;\ 3)$ tangents extérieurement en

$I.$

Soit

$(\Delta)$ une droite tangente à

$(\mathcal{C})\$ et à

$\ (\mathcal{C}')$ respectivement en

$A\$ et

$\ B\;,\ (A\neq B).$

$(\Delta)$ coupe

$(OO')$ en

$P.$

1) Démontrons que la droite

$(OA)$ est parallèle à la droite

$(O'B)$

On a :

$(\Delta)$ tangente à

$(\mathcal{C})$ en

$A$ alors,

$(OA)$ est perpendiculaire à

$(\Delta)$

aussi,

$(\Delta)$ tangente à

$(\mathcal{C}')$ au point

$B$ donc,

$(O'B)$ perpendiculaire à

$(\Delta)$

Ainsi,

$(OA)\$ et

$\ (O'B)$ sont deux droites perpendiculaires à une même droite

$(\Delta).$

Par conséquent,

$(OA)\$ et

$\ (O'B)$ sont parallèles.

2) a) On pose

$PO=x$ ; exprimons

$PO'$ en fonction de

$x$

On a :

$\begin{array}{rcl} PO'&=&PO+OO'\quad\text{or, }\ OO'=OI+IO'\\\\&=&PO+OI+IO'\\\\&=&x+1.5+3\\\\&=&x+4.5\end{array}$

D'où,

$\boxed{PO'=x+4.5}$

Calculons

$PO$

Comme

$PO=x$ alors, calculer

$PO$ revient à trouver la valeur de

$x$

On a :

$(PO')\$ et

$\ (PB)$ deux droites sécantes coupées par deux droites parallèles

$(OA)\$ et

$\ (O'B)$ donc, les triangles

$POA\$ et

$\ PO'B$ sont en position de Thalès.

Par suite, en appliquant le théorème de Thalès, on obtient :

$\dfrac{PO}{PO'}=\dfrac{OA}{O'B}=\dfrac{PA}{PB}$

Ainsi,

$\begin{array}{rcl}\dfrac{PO}{PO'}=\dfrac{OA}{O'B}&\Rightarrow&\dfrac{x}{x+4.5}=\dfrac{1.5}{3}\\ \\&\Rightarrow&3x=1.5(x+4.5)\\ \\&\Rightarrow&3x-1.5x=1.5\times 4.5\\ \\&\Rightarrow&1.5x=6.75\\ \\&\Rightarrow&x=\dfrac{6.75}{1.5}\\ \\&\Rightarrow&x=4.5\end{array}$

D'où,

$x=4.5\$ or,

$PO=x$

Par conséquent,

$\boxed{PO=4.5}$

b) En déduisons la valeur exacte de

$PA$

$PAO$ est un triangle rectangle en

$A$ donc, d'après le théorème de Pythagore, on a :

$PO^{2}=PA^{2}+OA^{2}$

Ainsi,

$\begin{array}{rcl} PO^{2}=PA^{2}+OA^{2}&\Rightarrow&PA^{2}=PO^{2}-OA^{2}\\ \\&\Rightarrow&PA=\sqrt{PO^{2}-OA^{2}}\\ \\&\Rightarrow&PA=\sqrt{20.25-2.25}\\ \\&\Rightarrow&PA=\sqrt{18}\\ \\&\Rightarrow&PA=3\sqrt{2}\end{array}$

D'où,

$\boxed{PA=3\sqrt{2}}$

c) Démontrons que

$PI=6$

On a :

$PI=PO+OI\$ or,

$PO=4.5\$ et

$\ OI=1.5$

Par suite :

$PI=4.5+1.5=6$

3) Soit

$I'$ le point de

$[AB]$ tel que

$PI'=4\sqrt{2}.$ Démontrons que les droites

$(OA)\$ et

$\ (II')$ sont parallèles.

Considérons

$P\;,\ A\;,\ I'$ trois points alignés d'une part, et

$P\;,\ O\;,\ I$ trois points alignés d'autre part, dans le même ordre.

Calculons les rapports

$\dfrac{PA}{PI'}\quad\text{et}\quad\dfrac{PO}{PI}$

On a :

$\dfrac{PA}{PI'}=\dfrac{3\sqrt{2}}{4\sqrt{2}}=\dfrac{3}{4}=0.75$

$\dfrac{PO}{PI}=\dfrac{4.5}{6}=0.75$

Ce qui montre que :

$\dfrac{PA}{PI'}=\dfrac{PO}{PI}$

Par conséquent, la réciproque du théorème de Thalès permet de conclure que les droites

$(OA)\$ et

$\ (II')$ sont parallèles.

Exercice 7

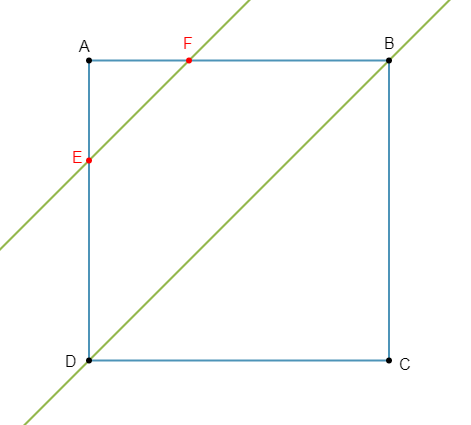
$ABCD$ est un carré.

$E$ est le point de

$[AD]$ tel que

$AE=\dfrac{1}{3}AD.$

$F$ est le point de

$[AB]$ tel que

$AF=\dfrac{1}{3}AB.$

1) Démontrons que les droites

$(EF)\$ et

$\ (BD)$ sont parallèles.

On a :

$A\;,\ F\;,\ B$ sont trois points alignés d'une part, et

$A\;,\ E\;,\ D$ sont trois points alignés d'autre part, dans le même ordre.

Calculons les rapports

$\dfrac{AF}{AB}\quad\text{et}\quad\dfrac{AE}{AD}$

On a :

$AF=\dfrac{1}{3}AB\ \Rightarrow\ \dfrac{AF}{AB}=\dfrac{1}{3}$

$AE=\dfrac{1}{3}AD\ \Rightarrow\ \dfrac{AE}{AD}=\dfrac{1}{3}$

On constate alors que :

$\dfrac{AF}{AB}=\dfrac{AE}{AD}$

Ainsi, d'après la réciproque du théorème de Thalès, les droites

$(EF)\$ et

$\ (BD)$ sont parallèles.

2) a) Pour obtenir la longueur

$EF$ , on doit multiplier la longueur

$BD$ par

$\dfrac{1}{3}.$

Justifions la réponse.

En effet, les droites

$(EF)\$ et

$\ (BD)$ étant parallèles alors, les triangles

$AEF\$ et

$\ ABD$ sont en position de Thalès.

Donc, d'après le théorème de Thalès, les longueurs des côtés correspondants sont proportionnelles.

Par suite, le triangle

$AEF$ est une réduction du triangle

$ABD.$

Or,

$\dfrac{AF}{AB}=\dfrac{AE}{AD}=\dfrac{1}{3}$ donc, le coefficient de réduction est égal à :

$\dfrac{1}{3}.$

Par conséquent,

$\boxed{EF=\dfrac{1}{3}\times BD}$

b) Pour obtenir l'aire de

$AEF$ , on doit multiplier l'aire du triangle

$ABD$ par

$\left(\dfrac{1}{3}\right)^{2}.$

Justifions

En effet, les triangles

$AEF\$ et

$\ ABD$ étant en position de Thalès avec un coefficient de réduction de

$\dfrac{1}{3}$ alors, le coefficient de réduction des aires est égal à

$\left(\dfrac{1}{3}\right)^{2}.$ Soit :

$\dfrac{1}{9}.$

D'où,

$\boxed{\text{Aire}(AEF)=\dfrac{1}{9}\times \text{Aire}(ABD)}$

Exercice 8

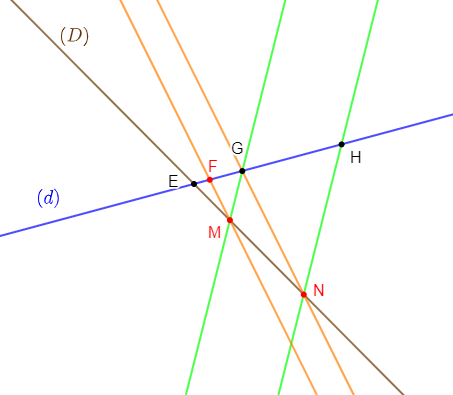
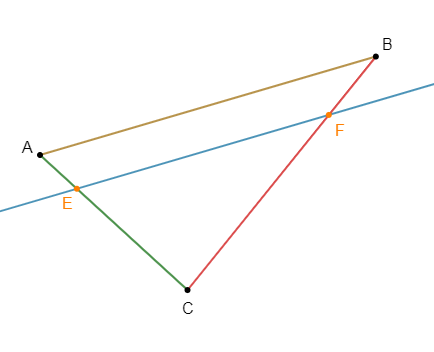
On donne trois points du plan

$E\;,\ G\$ et

$\ H$ alignés dans cet ordre sur une droite

$(d)$ tels que

$EG=1\,cm\$ et

$\ EH=x.$

$x$ est un réel positif.

Sur une droite

$(D)$ passant par

$E$ et distincte de

$(d)$ , on prend deux points

$M$ et

$N$ tels que

$(GM)\parallel(HN)$ et un point

$F$ sur

$(d)$ tel que

$(FM)\parallel(GN).$

1) Faisons la figure

Démontrons que

$EG^{2}=EF\times EH.$

En effet, les droites

$(GM)\$ et

$\ (HN)$ étant parallèles alors, les triangles

$EGM\$ et

$\ EHN$ sont en position de Thalès.

Donc, en appliquant le théorème de Thalès, on a :

$\dfrac{EG}{EH}=\dfrac{EM}{EN}\quad(1)$

De la même manière, les droites

$(FM)\$ et

$\ (GN)$ étant parallèles alors, les triangles

$EFM\$ et

$\ EGN$ sont en position de Thalès.

Ainsi, d'après le théorème de Thalès, on a :

$\dfrac{EF}{EG}=\dfrac{EM}{EN}\quad(2)$

En comparant les égalités

$(1)\$ et

$\ (2)$ , on peut alors écrire :

$\dfrac{EG}{EH}=\dfrac{EF}{EG}$

Par suite,

$\begin{array}{rcl}\dfrac{EG}{EH}=\dfrac{EF}{EG}&\Leftrightarrow&EG\times EG=EF\times EH\\\\&\Leftrightarrow&EG^{2}=EF\times EH\end{array}$

D'où,

$\boxed{EG^{2}=EF\times EH}$

2) Calculons

$EF$ en fonction de

$x.$

D'après le résultat de la question

$1)$ , on a :

$EG^{2}=EF\times EH.$

Ce qui donne :

$EF=\dfrac{EG^{2}}{EH}$

Alors, en remplaçant

$EG\$ et

$\ EH$ par leur valeur, on obtient :

$\begin{array}{rcl}EF&=&\dfrac{EG^{2}}{EH}\\\\&=&\dfrac{1^{2}}{x}\\\\&=&\dfrac{1}{x}\end{array}$

D'où,

$\boxed{EF=\dfrac{1}{x}}$

Exercice 9

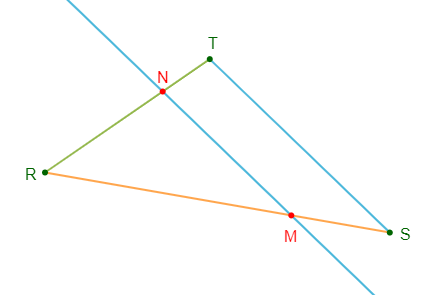
Construisons un triangle

$RTS$ tel que :

$RT=4\;cm\;;\ RS=7\;cm\;;\ ST= 5\;cm$

1) Le triangle

$RTS$ n'est pas rectangle.

Justifions :

Pour cela, on va vérifier si le carré de la longueur du plus grand côté est égal à la somme des carrés des longueurs des autres côtés.

On a :

$RS^{2}=7^{2}=49$

$RT^{2}=4^{2}=16$

$ST^{2}=5^{2}=25$

Alors,

$RT^{2}+ST^{2}=16+25=41$

Or,

$41\neq 49$

Ce qui signifie que

$RS^{2}$ n'est pas égale à

$RT^{2}+ST^{2}.$

Par conséquent, le théorème de Pythagore n'est pas vérifié.

D'où, le triangle

$RTS$ n'est pas rectangle.

2) Marquons un point

$M$ sur

$[RS]$ tel que

$RM=5\;cm$ puis traçons la droite passant par

$M$ et parallèle à la droite

$(ST)$ , elle coupe

$(RT)$ en

$N.$

Calculons

$MN\$ et

$\ NT.$

$-\$ Calcul de

$MN$

En effet, comme les droites

$(MN)\$ et

$\ (ST)$ sont parallèles alors, les triangles

$RMN\$ et

$\ RTS$ sont en position de Thalès.

Donc, en appliquant le théorème de Thalès, on a :

$\dfrac{MN}{ST}=\dfrac{RM}{RS}$

Alors, en remplaçant

$ST\;,\ RM\$ et

$\ RS$ par leur valeur, on obtient :

$\begin{array}{rcl}\dfrac{MN}{5}=\dfrac{5}{7}&\Rightarrow&7\times MN=5\times 5\\\\&\Rightarrow&MN=\dfrac{25}{7}\end{array}$

D'où,

$\boxed{MN=\dfrac{25}{7}}$

$-\$ Calcul de

$NT$

En effet, les droites

$(MN)\$ et

$\ (ST)$ sont parallèles alors, les triangles

$RMN\$ et

$\ RTS$ sont en position de Thalès.

Donc, en d'après le théorème de Thalès, on a :

$\dfrac{NT}{RT}=\dfrac{MS}{RS}$

Or,

$MS=RS-RM=7-5=2\,cm$

Ainsi, en remplaçant

$RT\;,\ MS\$ et

$\ RS$ par leur valeur, on obtient :

$\begin{array}{rcl}\dfrac{NT}{4}=\dfrac{2}{7}&\Rightarrow&7\times NT=4\times 2\\\\&\Rightarrow&NT=\dfrac{8}{7}\end{array}$

D'où,

$\boxed{NT=\dfrac{8}{7}}$

3) On donne

$MN=k\times TS\$ et

$\ Aire(RTS)=m\times Aire(RMN).$

Déterminons la valeur de

$k$ puis la valeur de

$m.$

$-\$ valeur de

$k$

On a :

$MN=k\times TS$

Ce qui donne :

$k=\dfrac{MN}{TS}$

En calculant, on trouve :

$\begin{array}{rcl} k&=&\dfrac{MN}{TS}\\\\&=&\dfrac{\dfrac{25}{7}}{5}\\\\&=&\dfrac{25}{7}\times\dfrac{1}{5}\\\\&=&\dfrac{5}{7}\end{array}$

D'où,

$\boxed{k=\dfrac{5}{7}}$

Ainsi,

$MN=\dfrac{5}{7}\times TS$

$-\$ valeur de

$m$

En effet, comme les triangles

$RMN\$ et

$\ RTS$ sont en position de Thalès alors,

$k$ est le coefficient de réduction.

Par suite,

$k^{2}$ sera le coefficient de réduction des aires.

Ce qui signifie :

$Aire(RMN)=k^{2}\times Aire(RTS)$

Ce qui donne alors,

$Aire(RTS)=\dfrac{Aire(RMN)}{k^{2}}$

En calculant, on trouve :

$\begin{array}{rcl} Aire(RTS)&=&\dfrac{Aire(RMN)}{k^{2}}\\\\&=&\dfrac{Aire(RMN)}{\left(\dfrac{5}{7}\right)^{2}}\\\\&=&\dfrac{Aire(RMN)}{\dfrac{25}{49}}\\\\&=&\dfrac{49}{25}\times Aire(RMN)\end{array}$

Ainsi,

$Aire(RTS)=\dfrac{49}{25}\times Aire(RMN)$

D'où,

$\boxed{m=\dfrac{49}{25}}$

Exercice 10

Soit le triangle

$ABC$ tel que :

$AB=5.2\;cm\;,\ BC=3.9\;cm\ \text{ et }\ AC=4.8\;cm$

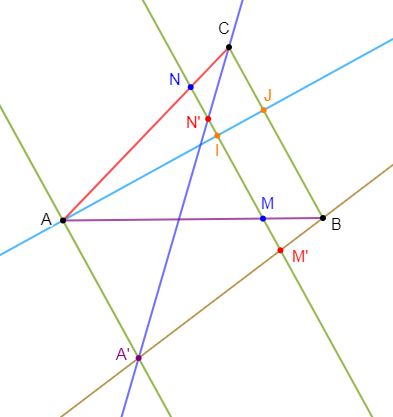
$M$ est le point du côté

$[AB]$ tel que

$AM=4\;cm.$

1) La parallèle à

$(BC)$ passant par

$M$ coupe le côté

$[AC]$ en

$N.$

Calculons la longueur

$MN.$

En effet, on a :

$(MN)$ parallèle à

$(BC).$

Alors, les triangles

$AMN\$ et

$\ ABC$ sont en position de Thalès.

Donc, en utilisant le théorème de Thalès, on a :

$\dfrac{MN}{BC}=\dfrac{AM}{AB}$

Ainsi, en remplaçant

$BC\;,\ AM\$ et

$\ AB$ par leur valeur, on obtient :

$\begin{array}{rcl}\dfrac{MN}{3.9}=\dfrac{4}{5.2}&\Rightarrow&5.2\times MN=3.9\times 4\\\\&\Rightarrow&MN=\dfrac{15.6}{5.2}\\\\&\Rightarrow&MN=3\end{array}$

D'où,

$\boxed{MN=3\;cm}$

2) La perpendiculaire à

$(BC)$ passant par

$A$ coupe

$(MN)$ en

$I\$ et

$\ (BC)$ en

$J.$

Calculons

$\dfrac{AI}{AJ}.$

En effet, les droites

$(MI)\$ et

$\ (BJ)$ étant parallèles alors, les triangles

$AIM\$ et

$\ ABJ$ sont en position de Thalès.

Donc, en appliquant le théorème de Thalès, on obtient :

$\dfrac{AI}{AJ}=\dfrac{AM}{AB}$

Ainsi, en remplaçant

$AM\$ et

$\ AB$ par leur valeur, on obtient :

$\dfrac{AI}{AJ}=\dfrac{4}{5.2}=0.77$

D'où,

$\boxed{\dfrac{AI}{AJ}=0.77}$

3) Soit

$A'$ un point de la parallèle à

$(BC)$ passant par

$A$ , on appelle respectivement

$M'\$ et

$\ N'$ les intersections de

$(A'B)\$ et

$\ (A'C)$ avec la droite

$(MN).$

a) Calculons

$\dfrac{A'M'}{A'B}.$

On a :

$(MM')$ parallèle à

$(AA').$

Alors, les triangles

$ABA'\$ et

$\ BMM'$ sont en position de Thalès.

Donc, en utilisant le théorème de Thalès, on a :

$\dfrac{A'M'}{A'B}=\dfrac{AM}{AB}$

Ainsi, en remplaçant

$AM\$ et

$\ AB$ par leur valeur, on obtient :

$\dfrac{A'M'}{A'B}=\dfrac{4}{5.2}=0.77$

D'où,

$\boxed{\dfrac{A'M'}{A'B}=0.77}$

b) Calculons

$M'N'.$

En effet, les droites

$(M'N')\$ et

$\ (BC)$ étant parallèles alors, les triangles

$AM'N'\$ et

$\ ABC$ sont en position de Thalès.

Donc, en appliquant le théorème de Thalès, on obtient :

$\dfrac{M'N'}{BC}=\dfrac{A'M'}{A'B}$

Or, d'après la question

$a)$ , on a :

$\dfrac{A'M'}{A'B}=0.77$

Ainsi, en remplaçant

$BC\$ et

$\ \dfrac{A'M'}{A'B}$ par leur valeur, on obtient :

$\begin{array}{rcl}\dfrac{M'N'}{3.9}=0.77&\Rightarrow&M'N'=3.9\times 0.77\\\\&\Rightarrow&M'N'=3\end{array}$

D'où,

$\boxed{M'N'=3\;cm}$

Exercice 11

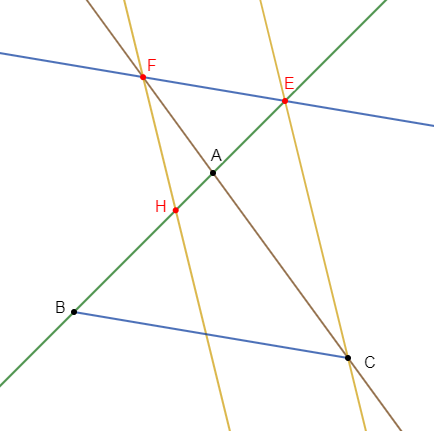
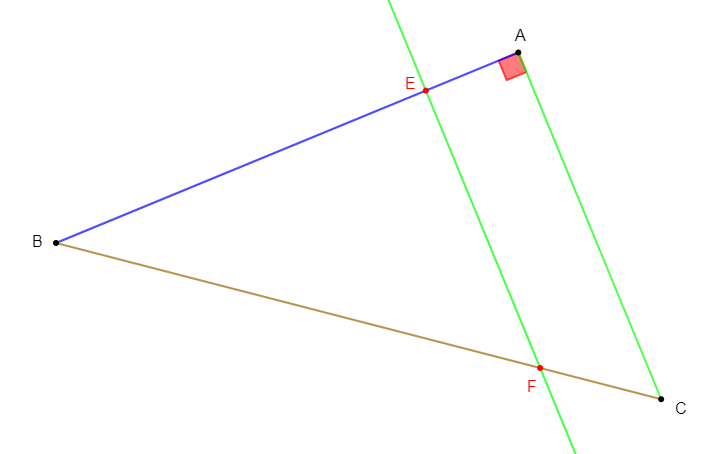
$ABC$ est un triangle

$E$ est un point de la droite

$(AB).$

La droite passant par

$E$ et parallèle à la droite

$(BC)$ coupe la droite

$(AC)$ au point

$F.$

La droite passant par

$F$ et parallèle à la droite

$(EC)$ coupe la droite

$(AB)$ au point

$H.$

Démontrons que

$AE^{2}=AH\times AB.$

En effet, les droites

$(BC)\$ et

$\ (EF)$ étant parallèles alors, les triangles

$AEF\$ et

$\ ABC$ sont en position de Thalès.

Donc, en appliquant le théorème de Thalès, on a :

$\dfrac{AE}{AB}=\dfrac{AF}{AC}\quad(1)$

De la même manière, les droites

$(FH)\$ et

$\ (EC)$ étant parallèles alors, les triangles

$AFH\$ et

$\ AEC$ sont en position de Thalès.

Ainsi, d'après le théorème de Thalès, on a :

$\dfrac{AH}{AE}=\dfrac{AF}{AC}\quad(2)$

En comparant les égalités

$(1)\$ et

$\ (2)$ , on peut alors écrire :

$\dfrac{AE}{AB}=\dfrac{AH}{AE}$

Par suite,

$\begin{array}{rcl}\dfrac{AE}{AB}=\dfrac{AH}{AE}&\Leftrightarrow&AE\times AE=AH\times AB\\\\&\Leftrightarrow&AE^{2}=AH\times AB\end{array}$

D'où,

$\boxed{AE^{2}=AH\times AB}$

Exercice 12

$ABC$ est un triangle tel que

$AB=7\;cm\;,\ BC=6\;cm\$ et

$\ AC=4\,cm.$

Soit

$E$ le point de

$[AC]$ tel que :

$CE=3\;cm.$

La parallèle à

$(AB)$ passant par

$E$ coupe

$[BC]$ en

$F.$

Calculons

$CF\$ et

$\ EF.$

En effet, les droites

$(AB)\$ et

$\ (EF)$ étant parallèles alors, les triangles

$ABC\$ et

$\ CEF$ sont en position de Thalès.

Ainsi, d'après le théorème de Thalès, on a :

$\dfrac{CF}{BC}=\dfrac{CE}{AC}$

Alors, en remplaçant

$BC\;,\ AC\$ et

$\ CE$ par leur valeur, on obtient :

$\begin{array}{rcl}\dfrac{CF}{6}=\dfrac{3}{4}&\Leftrightarrow&4\times CF=6\times 3\\\\&\Leftrightarrow&CF=\dfrac{18}{4}\\\\&\Leftrightarrow&CF=4.5\end{array}$

D'où,

$\boxed{CF=4.5\;cm}$

En utilisant encore le théorème de Thalès, on a :

$\dfrac{EF}{AB}=\dfrac{CE}{AC}$

Donc, en remplaçant

$AB\;,\ AC\$ et

$\ CE$ par leur valeur, on obtient :

$\begin{array}{rcl}\dfrac{EF}{7}=\dfrac{3}{4}&\Leftrightarrow&4\times EF=7\times 3\\\\&\Leftrightarrow&EF=\dfrac{21}{4}\\\\&\Leftrightarrow&EF=5.25\end{array}$

Ainsi,

$\boxed{EF=5.25\;cm}$

Exercice 13

Dans le plan, on considère un triangle

$ABC$ rectangle en

$B$ tel que :

$AB=2\;cm\$ et

$\ BC=1\;cm.$

1) Faisons une figure complète.

Calculons

$AC.$

Comme

$ABC$ est un triangle rectangle en

$B$ alors, d'après le théorème de Pythagore, on a :

$AC^{2}=AB^{2}+BC^{2}$

Ainsi,

$\begin{array}{rcl} AC^{2}=AB^{2}+BC^{2}&\Rightarrow&AC=\sqrt{AB^{2}+BC^{2}}\\ \\&\Rightarrow&AC=\sqrt{2^{2}+1^{2}}\\ \\&\Rightarrow&AC=\sqrt{4+1}\\ \\&\Rightarrow&AC=\sqrt{5}\end{array}$

D'où,

$\boxed{AC=\sqrt{5}}$

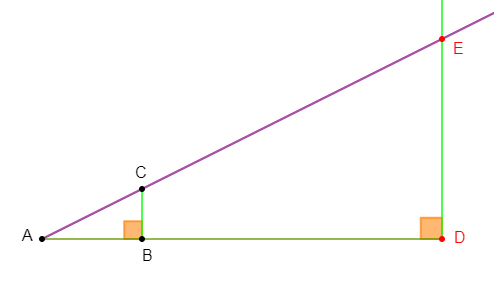
2) On considère le point

$D$ , tel que :

$B$ soit un point du segment

$[AD]\$ et

$\ AD=8\;cm.$

3) a) Soit

$E$ le point de la droite

$(AC)$ dont la projection orthogonale sur

$(AB)$ est le point

$D.$

b) Montrons que les droites

$(BC)\$ et

$\ (DE)$ sont parallèles.

On a :

$(BC)\$ et

$\ (DE)$ sont deux droites perpendiculaires à la droite

$(AB).$

Or, on sait que deux droites sont perpendiculaires à une même droite sont parallèles.

Par conséquent,

$(BC)\$ et

$\ (DE)$ sont parallèles.

c) Calculons les distances

$AE\$ et

$\ DE.$

Les droites

$(BC)\$ et

$\ (DE)$ étant parallèles alors, les triangles

$ABC\$ et

$\ ADE$ sont en position de Thalès.

Ainsi, d'après le théorème de Thalès, on a :

$\dfrac{AE}{AC}=\dfrac{AD}{AB}$

Alors, en remplaçant

$AC\;,\ AD\$ et

$\ AB$ par leur valeur, on obtient :

$\begin{array}{rcl}\dfrac{AE}{\sqrt{5}}=\dfrac{8}{2}&\Leftrightarrow&AE=4\times\sqrt{5}\\\\&\Leftrightarrow&AE=4\sqrt{5}\end{array}$

D'où,

$\boxed{AE=4\sqrt{5}}$

En appliquant encore le théorème de Thalès, on a :

$\dfrac{DE}{BC}=\dfrac{AD}{AB}$

Donc, en remplaçant

$BC\;,\ AD\$ et

$\ AB$ par leur valeur, on obtient :

$\begin{array}{rcl}\dfrac{DE}{1}=\dfrac{8}{2}&\Rightarrow&DE=4\end{array}$

D'où,

$\boxed{DE=4}$

4) Calculons l'aire de

$ABC$ et le coefficient

$K$ de réduction des longueurs.

L'aire du triangle

$ABC$ est donnée par :

$\begin{array}{rcl}\text{Aire}(ABC)&=&\dfrac{AB\times BC}{2}\\\\&=&\dfrac{2\times 1}{2}\\\\&=&\dfrac{2}{2}\\\\&=&1\end{array}$

D'où,

$\boxed{\text{Aire}(ABC)=1\;cm^{2}}$

Le coefficient

$K$ de réduction des longueurs est donné par :

$K=\dfrac{BC}{DE}=\dfrac{1}{4}$

Donc,

$\boxed{K=\dfrac{1}{4}}$

En déduisons l'aire de

$ADE.$

En effet, on sait que si le coefficient de réduction des longueurs est

$K$ alors, le coefficient de réduction des aires est égal à

$K^{2}.$

Ce qui signifie :

$\text{Aire}(ABC)=K^{2}\times\text{Aire}(ADE)$

Ainsi,

$\text{Aire}(ADE)=\dfrac{\text{Aire}(ABC)}{K^{2}}$

En remplaçant,

$\text{Aire}(ABC)\$ et

$\ K$ par leur valeur, on obtient :

$\begin{array}{rcl}\text{Aire}(ADE)&=&\dfrac{\text{Aire}(ABC)}{K^{2}}\\\\&=&\dfrac{1}{\left(\dfrac{1}{4}\right)^{2}}\\\\&=&\dfrac{1}{\dfrac{1}{16}}\\\\&=&16\end{array}$

D'où,

$\boxed{\text{Aire}(ADE)=16\;cm^{2}}$

Exercice 14

Soit

$ABC$ un triangle tel que :

$AB=10\,cm\;,\ AC=7.5\,cm\ \text{ et }\ BC=12.5\,cm$

1) Montrons que

$ABC$ est un triangle rectangle en

$A.$

Pour cela, calculons les carrés des longueurs des côtés du triangle.

On a :

$BC^{2}=(12.5)^{2}=156.25$

$AB^{2}=10^{2}=100$

$AC^{2}=(7.5)^{2}=56.25$

Alors,

$AB^{2}+AC^{2}=100+56.25=156.25$

On constate que :

$AB^{2}+AC^{2}=BC^{2}$

Par conséquent, d'après la réciproque du théorème de Pythagore, le triangle

$ABC$ est rectangle en

$A.$

2) Soit

$E$ le point du segment

$[AB]$ tel que

$AE=2\,cm.$

La perpendiculaire à

$(AB)$ passant par

$E$ coupe

$(BC)$ au point

$F.$

a) Montrons que

$(AC)\$ et

$\ (EF)$ sont parallèles.

On a :

$(AC)\$ et

$\ (EF)$ sont deux droites perpendiculaires à la droite

$(AB).$

Or, on sait que deux droites sont perpendiculaires à une même droite sont parallèles.

Par conséquent,

$(AC)\$ et

$\ (EF)$ sont parallèles.

b) Calculons les distances

$BE\;,\ EF\$ et

$\ BF.$

$-\$ Calcul de

$BE$

Comme

$E\in[AB]$ alors,

$BE=AB-AE$

En remplaçant

$AB\$ et

$\ AE$ par leur valeur, on trouve :

$BE=10-2=8$

D'où,

$\boxed{BE=8\;cm}$

$-\$ Calcul de

$EF$

Les droites

$(AC)\$ et

$\ (EF)$ étant parallèles alors, les triangles

$ABC\$ et

$\ AEF$ sont en position de Thalès.

Ainsi, d'après le théorème de Thalès, on a :

$\dfrac{EF}{AC}=\dfrac{BE}{AB}$

Alors, en remplaçant

$AC\;,\ BE\$ et

$\ AB$ par leur valeur, on obtient :

$\begin{array}{rcl}\dfrac{EF}{7.5}=\dfrac{8}{10}&\Leftrightarrow&10\times EF=7.5\times 8\\\\&\Leftrightarrow&EF=\dfrac{60}{10}\\\\&\Leftrightarrow&EF=6\end{array}$

D'où,

$\boxed{EF=6\;cm}$

$-\$ Calcul de

$BF$

En appliquant encore le théorème de Thalès, on a :

$\dfrac{BF}{BC}=\dfrac{BE}{AB}$

Donc, en remplaçant

$BC\;,\ BE\$ et

$\ AB$ par leur valeur, on obtient :

$\begin{array}{rcl}\dfrac{BF}{12.5}=\dfrac{8}{10}&\Leftrightarrow&10\times BF=12.5\times 8\\\\&\Leftrightarrow&BF=\dfrac{100}{10}\\\\&\Leftrightarrow&BF=10\end{array}$

D'où,

$\boxed{BF=10\;cm}$

Exercice 15

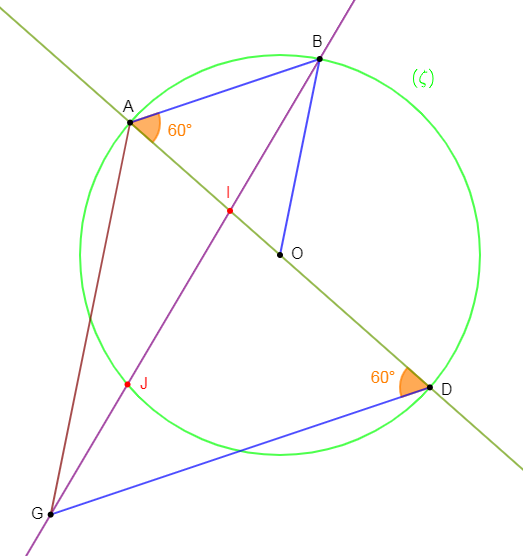
1) Soit un cercle

$(\zeta)$ de centre

$O$ et de rayon

$4\,cm\;,\ [AD]$ un de ses diamètres.

a) D'un côté de la droite

$(AD)$ , construisons le point

$G$ tel que le triangle

$ADG$ soit équilatéral.

b) De l'autre côté de la droite

$(AD)$ , plaçons le point

$B$ du cercle

$(\zeta)$ , tel que

$AB=4\,cm.$

2) Démontrons que le triangle

$OAB$ est équilatéral.

En effet, comme

$A\$ et

$\ B$ appartiennent au cercle

$(\zeta)$ alors, les longueurs

$OA\$ et

$\ OB$ sont égales au rayon de

$(\zeta).$

Ce qui signifie que :

$OA=OB=4\,cm$

De plus, on sait que :

$AB=4\,cm$

Donc,

$OA=OB=AB=4\,cm$

Ainsi, le triangle

$OAB$ a ses côtés de même longueur par conséquent, c'est un triangle équilatéral.

3) On admet que les angles

$\widehat{OAB}\$ et

$\ \widehat{ADG}$ sont égaux. En déduisons la position relative de

$(AB)\$ et

$\ (DG).$

En effet, les droites

$(AB)\$ et

$\ (DG)$ et la sécante

$(AD)$ déterminent deux angles alternes internes

$\widehat{OAB}\$ et

$\ \widehat{ADG}.$

Comme ces deux angles sont de même mesure alors, les droites

$(AB)\$ et

$\ (DG)$ sont parallèles.

4) La droite

$(BG)$ coupe le segment

$[AD]$ en

$I\$ et

$\ (\zeta)$ en

$J.$ En utilisant le théorème de Thalès justifions que :

$\dfrac{IA}{ID}=\dfrac{1}{2}$

En effet, les droites

$(AD)\$ et

$\ (BG)$ sécantes en

$I$ sont coupées par deux droites

$(AB)\$ et

$\ (DG).$

Or, d'après le résultat de la question

$3)$ , on a :

$(AB)\$ et

$\ (DG)$ sont parallèles.

Donc, les triangles

$AIB\$ et

$\ DIG$ sont en position de Thalès.

Ainsi, en utilisant le théorème de Thalès, on a :

$\dfrac{IA}{ID}=\dfrac{AB}{DG}$

Or, on sait que

$ADG$ est un triangle équilatéral.

Par conséquent :

$DG=AD$

Comme

$[AD]$ est un diamètre de

$(\zeta)$ alors, la longueur

$AD$ est égale au double du rayon de

$(\zeta).$

Donc,

$AD=2\times 4\,cm=8\,cm$

Par suite,

$DG=8\,cm$

Ainsi, dans l'égalité

$\dfrac{IA}{ID}=\dfrac{AB}{DG}$ , en remplaçant

$AB\$ et

$\ DG$ par leur valeur, on obtient :

$\begin{array}{rcl}\dfrac{IA}{ID}&=&\dfrac{AB}{DG}\\\\&=&\dfrac{4}{8}\\\\&=&\dfrac{4\div 4}{8\div 4}\\\\&=&\dfrac{1}{2}\end{array}$

D'où,

$\boxed{\dfrac{IA}{ID}=\dfrac{1}{2}}$

Exercice 16

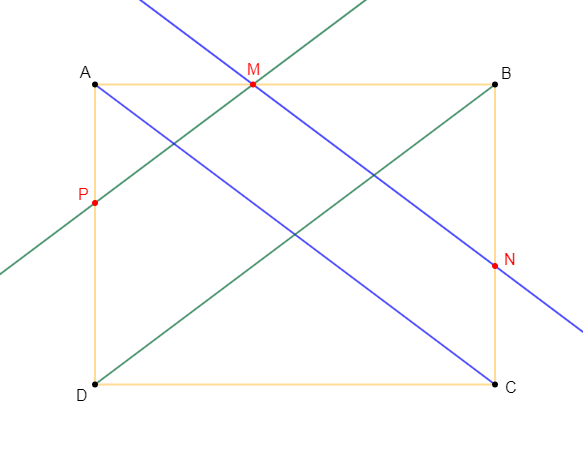
Construisons un rectangle

$ABCD$ tel que :

$AB=8\;cm\$ et

$\ AD=6\;cm.$ On désigne par

$M$ un point

$[AB]$ tel que

$AM=x.$

Par

$M$ , on trace la parallèle à

$(AC)$ qui coupe

$(BC)$ en

$N$ et la parallèle à

$(BD)$ qui coupe

$(AD)$ en

$P.$

1) Calculons

$AC$ puis exprimons

$MN\$ et

$\ MP$ en fonction de

$x.$

$-\$ Calcul de

$AC$

Comme

$ABCD$ est un rectangle alors, le triangle

$ABC$ est rectangle en

$B.$

Donc, en utilisant le théorème Pythagore, on a :

$\begin{array}{rcl} AC^{2}=AB^{2}+CC^{2}&\Rightarrow&AC=\sqrt{AB^{2}+BC^{2}}\\\\&\Rightarrow&AC=\sqrt{8^{2}+6^{2}}\\\\&\Rightarrow&AC=\sqrt{64+36}\\\\&\Rightarrow&AC=\sqrt{100}\\\\&\Rightarrow&AC=10\end{array}$

D'où,

$\boxed{AC=10\,cm}$

$-\$ Expression de

$MN$ en fonction de

$x$ x

Les droites

$(MN)\$ et

$\ (AC)$ étant parallèles alors, les triangles

$BNM\$ et

$\ BAC$ sont en position de Thalès.

Ainsi, d'après le théorème de Thalès, on obtient :

$\dfrac{MN}{AC}=\dfrac{MB}{AB}$

Or, on sait que :

$MB=AB-AM$

Donc, en remplaçant

$MB$ par

$AB-AM$ , on trouve :

$\dfrac{MN}{AC}=\dfrac{AB-AM}{AB}$

Par suite, en remplaçant

$AC\;,\ AB\$ et

$\ AM$ par leur valeur, on obtient :

$\begin{array}{rcl}\dfrac{MN}{AC}=\dfrac{AB-AM}{AB}&\Rightarrow&\dfrac{MN}{10}=\dfrac{8-x}{8}\\\\&\Rightarrow&8\times MN=10\times(8-x)\\\\&\Rightarrow&8\times MN=80-10x\\\\&\Rightarrow&MN=\dfrac{80-10x}{8}\\\\&\Rightarrow&MN=\dfrac{40-5x}{2}\\\\&\Rightarrow&MN=\dfrac{40}{2}-\dfrac{5x}{2}\\\\&\Rightarrow&MN=20-\dfrac{5x}{2}\end{array}$

D'où,

$\boxed{MN=20-\dfrac{5x}{2}}$

$-\$ Expression de

$MP$ en fonction de

$x$

En effet, comme les droites

$(MP)\$ et

$\ (BD)$ sont parallèles alors, les triangles

$AMP\$ et

$\ ABD$ sont en position de Thalès.

Ainsi, en appliquant le théorème de Thalès, on obtient :

$\dfrac{MP}{BD}=\dfrac{AM}{AB}$

Or, on sait que :

$ABCD$ est un rectangle donc, les diagonales

$[AC]\$ et

$\ [BD]$ ont même longueur.

Ainsi,

$BD=AC=10\,cm$

Par suite, en remplaçant

$AM\;,\ AB\$ et

$\ BD$ par leur valeur, on trouve :

$\begin{array}{rcl}\dfrac{MN}{BD}=\dfrac{AM}{AB}&\Rightarrow&\dfrac{MP}{10}=\dfrac{x}{8}\\\\&\Rightarrow&8\times MP=10\times x\\\\&\Rightarrow&MP=\dfrac{10x}{8}\\\\&\Rightarrow&MP=\dfrac{5x}{2}\end{array}$

D'où,

$\boxed{MP=\dfrac{5x}{2}}$

2) Montrons que

$MN+MP$ est indépendant de

$x.$

En calculant l'expression

$MN+MP$ , on a :

$\begin{array}{rcl} MN+MP&=&20-\dfrac{5x}{2}+\dfrac{5x}{2}\\\\&=&20+\dfrac{5x-5x}{2}\\\\&=&20\end{array}$

Donc,

$\boxed{MN+MP=20}$

On constate alors que l'expression

$MN+MP$ donne un résultat qui ne dépend pas de

$x.$

Par conséquent, on peut dire que

$MN+MP$ est indépendant de

$x.$

3) Déterminons les valeurs de

$x$ pour lesquelles

$MN=MP.$

En effet, on a :

$\begin{array}{rcl} MN=MP&\Leftrightarrow&20-\dfrac{5x}{2}=\dfrac{5x}{2}\\\\&\Leftrightarrow&-\dfrac{5x}{2}-\dfrac{5x}{2}=-20\\\\&\Leftrightarrow&\dfrac{-5x-5x}{2}=-20\\\\&\Leftrightarrow&\dfrac{-10x}{2}=-20\\\\&\Leftrightarrow&-5x=-20\\\\&\Leftrightarrow&x=\dfrac{-20}{-5}\\\\&\Leftrightarrow&x=4\end{array}$

D'où,

$\boxed{x=4}$

Ainsi, lorsque

$x$ est égal à

$4$ , les longueurs

$MN\$ et

$\ MP$ sont égales.

Exercice 17

1) Énonçons dans notre cahier le théorème de Thalès.

Si, deux droites sécantes sont coupées par deux droites parallèles alors, on obtient deux triangles dont les côtés correspondants ont des longueurs proportionnelles.

2) Énonçons dans notre cahier la réciproque du théorème de Thalès.

Si,

$A\;,\ M\$ et

$\ B$ trois points alignés d'une part,

$A\;,\ N\$ et

$\ C$ trois points alignés d'autre part, dans le même ordre tels que

$\dfrac{AM}{AB}=\dfrac{AN}{AC}$ alors, les droites

$(MN)\$ et

$\ (BC)$ sont parallèles.

On peut aussi utiliser l'égalité

$\dfrac{AM}{MB}=\dfrac{AN}{NC}$ ou encore

$\dfrac{MB}{AB}=\dfrac{NC}{AC}.$

Exercice 18

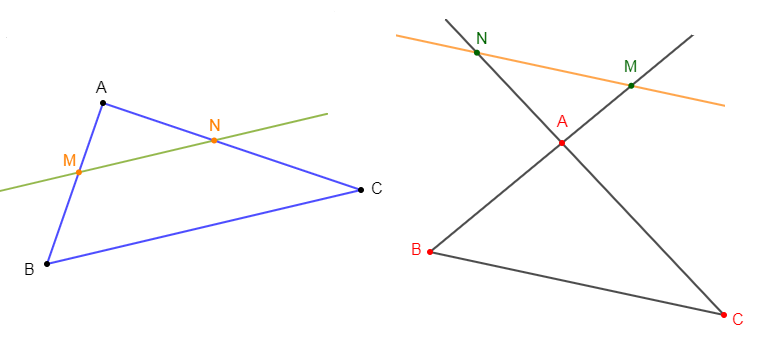
Donnons les figures présentant deux triangles en position de Thalès.

Dans les deux figures, on a :

$(MN)$ est parallèle à

$(BC)$

$M\in(AB)\$ et

$\ N\in(AC)$

Ainsi, dans chaque figure, les triangles

$ABC\$ et

$\ AMN$ sont en position de Thalès.

Exercice 19

Répondons par vrai ou faux :

$FEG$ est un triangle,

$M\in[FE]\$ et

$\ N\in[FG]$ tels que :

$(MN)\parallel (EG)$ , d'après la réciproque du théorème de Thalès

$\dfrac{FM}{FE}=\dfrac{FN}{FG}\quad\text{Faux}$

C'est le théorème de Thalès qui permet d'avoir cette égalité et non sa réciproque.

2) Si,

$MAN$ est un triangle ;

$M\;,\ I\;,\ A$ d'une part et

$M\;,\ J\;,\ N$ d'autre part sont alignés dans le même ordre et

$\dfrac{MI}{MA}=\dfrac{MN}{MJ}$ alors,

$(IJ)\parallel (AN)\quad\text{Faux}$

C'est l'égalité

$\dfrac{MI}{MA}=\dfrac{MJ}{MN}$ qui permet de conclure que

$(IJ)\parallel (AN).$

3) Si, deux triangles sont en position de Thalès alors, les supports de deux de leurs côtés sont parallèles.

$\quad\text{Vrai}$

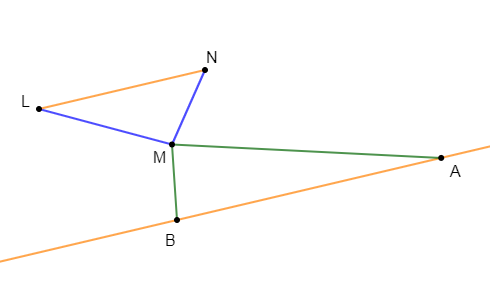
$MNL\$ et

$\ MAB$ sont deux triangles tels que

$(NL)\parallel (AB)$ alors,

$MNL\$ et

$\ MAB$ sont en position de Thalès.

$\quad\text{Faux}$

Pour cela, il faut ajouter la condition suivante :

$N\in(MA)\$ et

$\ L\in(MB).$

Exemple : Sur la figure ci-dessous, les droites

$(NL)\$ et

$\ (AB)$ sont parallèles mais les deux triangles

$MNL\$ et

$\ MAB$ ne sont pas en position de Thalès parce que les points

$A\;,\ M\;,\ L$ d'une part et

$B\;,\ M\;,\ N$ d'autre part, ne sont pas alignés.

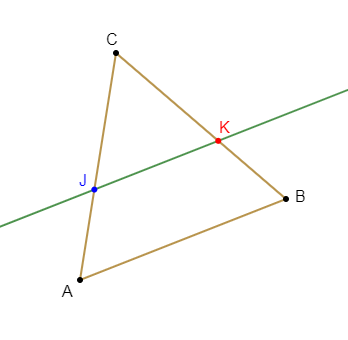
5) Si

$ABC$ est un triangle,

$K\in[BC]$ et la parallèle à

$(AB)$ passant par

$K$ coupe

$(AC)$ en

$J$ alors

$CKJ\$ et

$\ CBA$ sont des triangles en position de Thalès.

$\quad\text{Vrai}$

Exercice 20

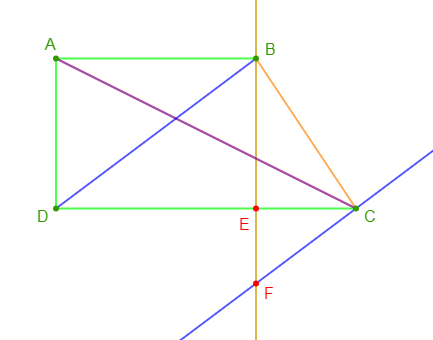
$ABCD$ est un trapèze rectangle tel que :

$AB=4\,cm\;,\ AD=3\,cm\ \text{ et }\ DC=6\,cm$

1) Faisons la figure en vraie grandeur.

2) Calculons

$BD\$ et

$\ AC.$

$-\$ Calcul de

$BD$

Le triangle

$ABD$ étant rectangle en

$A$ alors, en utilisant le théorème Pythagore, on obtient :

$\begin{array}{rcl} BD^{2}=AB^{2}+AD^{2}&\Rightarrow&BD=\sqrt{AB^{2}+AD^{2}}\\\\&\Rightarrow&BD=\sqrt{4^{2}+3^{2}}\\\\&\Rightarrow&BD=\sqrt{16+9}\\\\&\Rightarrow&BD=\sqrt{25}\\\\&\Rightarrow&BD=5\end{array}$

D'où,

$\boxed{BD=5\,cm}$

$-\$ Calcul de

$AC$

Comme le triangle

$ADC$ est rectangle en

$D$ alors, d'après le théorème Pythagore, on a :

$\begin{array}{rcl} AC^{2}=AD^{2}+DC^{2}&\Rightarrow&AC=\sqrt{AD^{2}+DC^{2}}\\\\&\Rightarrow&AC=\sqrt{3^{2}+6^{2}}\\\\&\Rightarrow&AC=\sqrt{9+36}\\\\&\Rightarrow&AC=\sqrt{45}\\\\&\Rightarrow&AC=\sqrt{9\times 5}\\\\&\Rightarrow&AC=\sqrt{9}\times\sqrt{5}\\\\&\Rightarrow&AC=3\sqrt{5}\end{array}$

D'où,

$\boxed{AC=3\sqrt{5}\,cm}$

3) La perpendiculaire à la droite

$(DC)$ passant par

$B$ coupe

$(DC)$ en

$E.$

Montrons que

$BC=\sqrt{13}.$

Comme

$(DC)$ est perpendiculaire à

$(BE)$ en

$E$ alors, le triangle

$BEC$ est rectangle en

$E.$

Donc, en appliquant le théorème Pythagore, on obtient :

$BC^{2}=BE^{2}+EC^{2}$

Or,

$EC=DC-DE\$ et

$\ DE=AB$

Donc,

$EC=DC-AB=6-4=2\,cm$

De plus,

$BE=AD=3\,cm$

Par suite, en remplaçant

$BE\$ et

$\ EC$ par leur valeur, on obtient :

$\begin{array}{rcl} BC^{2}=BE^{2}+EC^{2}&\Rightarrow&BC=\sqrt{BE^{2}+EC^{2}}\\\\&\Rightarrow&BC=\sqrt{3^{2}+2^{2}}\\\\&\Rightarrow&BC=\sqrt{9+4}\\\\&\Rightarrow&BC=\sqrt{13}\end{array}$

Ainsi,

$\boxed{BC=\sqrt{13}}$

4) Soit

$F$ le point de la droite

$(EB)$ n'appartenant pas à

$[BE]$ tel que

$EF=1.5\;cm.$

Démontrons que

$(CF)\$ et

$\ (DB)$ sont parallèles.

Considérons

$B\;,\ E\;,\ F$ trois points alignés d'une part, et

$D\;,\ E\;,\ C$ trois points alignés d'autre part, dans le même ordre.

Calculons les rapports

$\dfrac{EF}{EB}\quad\text{et}\quad\dfrac{EC}{ED}$

On a :

$\dfrac{EF}{EB}=\dfrac{1.5}{3}=0.5$

$\dfrac{EC}{ED}=\dfrac{2}{4}=0.5$

On constate alors :

$\dfrac{EF}{EB}=\dfrac{EC}{ED}$

Par conséquent, la réciproque du théorème de Thalès permet de conclure que les droites

$(CF)\$ et

$\ (DB)$ sont parallèles.

5) Calculons

$FC.$

En effet, les droites

$(CF)\$ et

$\ (DB)$ étant parallèles alors, les triangles

$BED\$ et

$\ CEF$ sont en position de Thalès.

Donc, en utilisant le théorème de Thalès, on a :

$\dfrac{FC}{BD}=\dfrac{EC}{ED}$

Ainsi, en remplaçant

$EC\$ et

$\ BD$ par leur valeur, on obtient :

$\begin{array}{rcl}\dfrac{FC}{BD}=\dfrac{EC}{ED}&\Rightarrow&\dfrac{FC}{5}=\dfrac{2}{4}\\\\&\Rightarrow&4\times FC=5\times 2\\\\&\Rightarrow&FC=\dfrac{10}{4}\\\\&\Rightarrow&FC=2.5\end{array}$

D'où,

$\boxed{FC=2.5\,cm}$

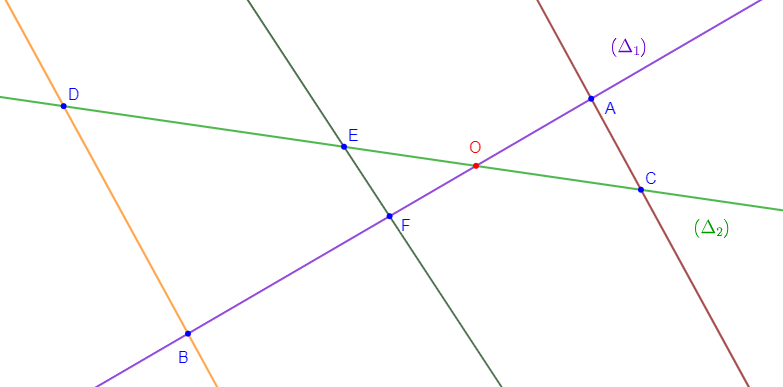
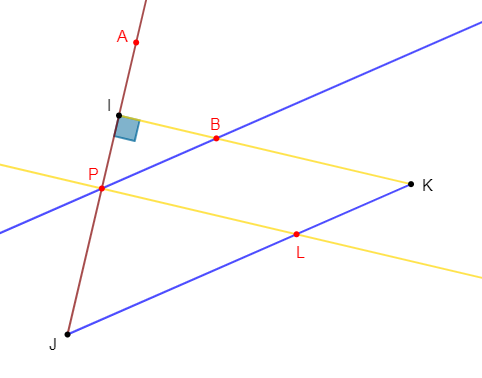
Exercice 21

$\left(\Delta_{1}\right)\$ et

$\ \left(\Delta_{2}\right)$ sont deux droites sécantes en

$O.$

$A\in\left(\Delta_{1}\right)\$ et

$\ B\in\left(\Delta_{1}\right)$

$C\in\left(\Delta_{2}\right)\$ et

$\ D\in\left(\Delta_{2}\right)$

$(AC)\parallel (BD)\$ et

$\ OA=4\;cm$

$OB=10\;cm\$ et

$\ OC=5\;cm.$

a) Faisons la figure.

b) Calculons

$OD.$

En effet, les droites

$(AC)\$ et

$\ (BD)$ étant parallèles alors, les triangles

$AOC\$ et

$\ ODB$ sont en position de Thalès.

Ainsi, en utilisant le théorème de Thalès, on a :

$\dfrac{OD}{OC}=\dfrac{OB}{OA}$

Alors, en remplaçant

$OC\;,\ OB\$ et

$\ OA$ par leur valeur, on obtient :

$\begin{array}{rcl}\dfrac{OD}{5}=\dfrac{10}{4}&\Rightarrow&4\times OD=5\times 10\\\\&\Rightarrow&OD=\dfrac{50}{4}\\\\&\Rightarrow&OD=12.5\end{array}$

D'où,

$\boxed{OD=12.5\;cm}$

$F\in\left(\Delta_{1}\right)\$ et

$\ E\in\left(\Delta_{2}\right)$ tels que :

$OF=3\;cm$ ,

$OE=4\;cm.$

On a :

$E\;,\ O\;,\ C$ sont trois points alignés d'une part, et

$A\;,\ O\;,\ F$ sont trois points alignés d'autre part, dans le même ordre.

En calculant les rapports

$\dfrac{OE}{OC}\$ et

$\ \dfrac{OF}{OA}$ , on trouve :

$\dfrac{OE}{OC}=\dfrac{4}{5}=0.8$

$\dfrac{OF}{OA}=\dfrac{3}{4}=0.75$

On constate alors que :

$\dfrac{OE}{OC}$ n'est pas égal à

$\dfrac{OF}{OA}.$

Par conséquent, les droites

$(EF)\$ et

$\ (BD)$ ne sont pas parallèles.

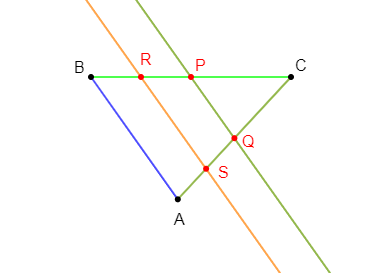
Exercice 22

1) Construisons un triangle

$ABC$ tel que :

$AB=4.5\;cm\;,\ AC=5\;cm\ \text{ et }\ BC=6\;cm$

2) Plaçons sur le segment

$[BC]$ le point

$P$ tel que

$CP=3\;cm$ et sur le segment

$[AC]$ le point

$Q$ tel que

$AQ=2.5\;cm.$

3) Démontrons que les droites

$(PQ)\$ et

$\ (AB)$ sont parallèles.

On a :

$C\;,\ P\;,\ B$ sont trois points alignés d'une part, et

$C\;,\ Q\;,\ A$ sont trois points alignés d'autre part, dans le même ordre.

Calculons les rapports

$\dfrac{CP}{BC}\$ et

$\ \dfrac{CQ}{AC}.$

On a :

$\dfrac{CP}{BC}=\dfrac{3}{6}=0.5$

$\dfrac{CQ}{AC}=\dfrac{AC-AQ}{AC}=\dfrac{5-2.5}{5}=\dfrac{2.5}{5}=0.5$

On constate alors que :

$\dfrac{CP}{BC}=\dfrac{CQ}{AC}.$

Par conséquent, d'après la réciproque du théorème de Thalès, les droites

$(PQ)\$ et

$\ (AB)$ sont parallèles.

4) Plaçons le point

$R$ sur le segment

$[BC]$ tel que

$CR=4.5\;cm.$

La parallèle à la droite

$(AB)$ passant par

$R$ coupe la droite

$(AC)$ en

$S.$

Calculons

$CS\$ et

$\ RS.$

$-\$ Calcul de

$CS$

Les droites

$(AB)\$ et

$\ (RS)$ étant parallèles alors, les triangles

$ABC\$ et

$\ CRS$ sont en position de Thalès.

Ainsi, en utilisant le théorème de Thalès, on a :

$\dfrac{CS}{AC}=\dfrac{CR}{BC}$

Alors, en remplaçant

$AC\;,\ CR\$ et

$\ BC$ par leur valeur, on obtient :

$\begin{array}{rcl}\dfrac{CS}{5}=\dfrac{4.5}{6}&\Leftrightarrow&6\times CS=4.5\times 5\\\\&\Leftrightarrow&CS=\dfrac{22.5}{6}\\\\&\Leftrightarrow&CS=3.75\end{array}$

D'où,

$\boxed{CS=3.75\;cm}$

$-\$ Calcul de

$RS$

En appliquant encore le théorème de Thalès, on a :

$\dfrac{RS}{AB}=\dfrac{CR}{BC}$

Donc, en remplaçant

$AB\;,\ CR\$ et

$\ BC$ par leur valeur, on obtient :

$\begin{array}{rcl}\dfrac{RS}{4.5}=\dfrac{4.5}{6}&\Leftrightarrow&6\times RS=4.5\times 4.5\\\\&\Leftrightarrow&RS=\dfrac{20.25}{6}\\\\&\Leftrightarrow&RS=3.375\end{array}$

D'où,

$\boxed{RS=3.375\;cm}$

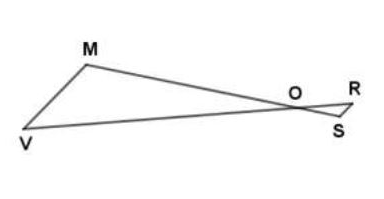
Exercice 23

Sur la figure ci-dessous,

$MO=7.5\;cm$ ,

$OV=18\;cm$ ,

$OS=1.5\;cm$ et

$OR=3.6\;cm$ ,

$RS=3\;cm.$

1) Montrons que les droites

$(MV)\$ et

$\ (RS)$ sont parallèles.

On a :

$M\;,\ O\;,\ S$ sont trois points alignés d'une part, et

$V\;,\ O\;,\ R$ sont trois points alignés d'autre part, dans le même ordre.

En calculant les rapports

$\dfrac{OS}{MO}\$ et

$\ \dfrac{OR}{OV}$ , on a :

$\dfrac{OS}{MO}=\dfrac{1.5}{7.5}=0.2$

$\dfrac{OR}{OV}=\dfrac{3.6}{18}=0.2$

On remarque alors que :

$\dfrac{OS}{MO}=\dfrac{OR}{OV}.$

Par conséquent, d'après la réciproque du théorème de Thalès, les droites

$(MV)\$ et

$\ (RS)$ sont parallèles.

2) Calculons

$VM.$

Comme les droites

$(MV)\$ et

$\ (RS)$ sont parallèles alors, les triangles

$OMV\$ et

$\ ORS$ sont en position de Thalès.

Ainsi, en appliquant le théorème de Thalès, on a :

$\dfrac{RS}{VM}=\dfrac{OR}{OV}$

Or,

$\dfrac{OR}{OV}=0.2$

Donc, en remplaçant

$RS\$ et

$\ \dfrac{OR}{OV}$ par leur valeur, on obtient :

$\begin{array}{rcl}\dfrac{3}{VM}=0.2&\Leftrightarrow&0.2\times VM=3\\\\&\Leftrightarrow&VM=\dfrac{3}{0.2}\\\\&\Leftrightarrow&VM=15\end{array}$

D'où,

$\boxed{VM=15\;cm}$

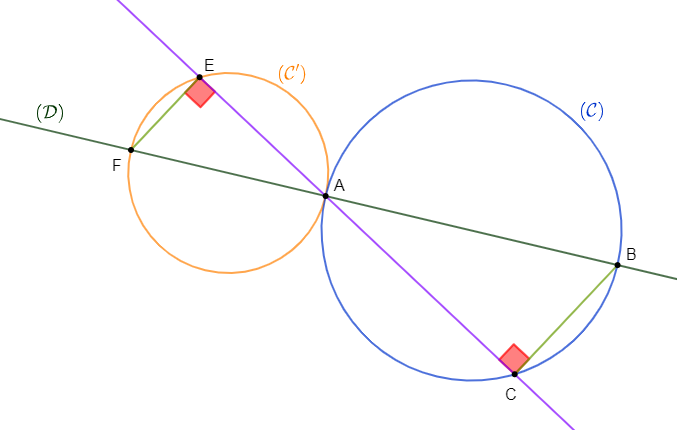
Exercice 24

Soient

$F\;,\ A\$ et

$\ B$ trois points alignés dans cet ordre sur une droite

$(\mathcal{D})$ tels que

$FA=4\;cm\$ et

$\ AB=6\;cm.$

$(\mathcal{C})\$ et

$\ (\mathcal{C}')$ sont deux cercles de diamètres respectifs

$[AB]\$ et

$\ [AF].$

Plaçons un point

$C$ sur le cercle

$(\mathcal{C})$ tel que

$BC=3\;cm.$

1) Le triangle

$ABC$ est rectangle en

$C.$

En effet, on remarque que

$ABC$ est un triangle inscrit dans le cercle

$(\mathcal{C})$ et dont le côté

$[AB]$ est un diamètre de ce cercle.

Par conséquent,

$ABC$ est un triangle rectangle en

$C.$

2) Calculons la longueur

$AC$

Comme

$ABC$ est un triangle rectangle en

$C$ alors, d'après le théorème de Pythagore, on a :

$AB^{2}=AC^{2}+BC^{2}$

Ainsi,

$\begin{array}{rcl} AB^{2}=AC^{2}+BC^{2}&\Rightarrow& AC^{2}=AB^{2}-BC^{2}\\\\&\Rightarrow&AC=\sqrt{AB^{2}-BC^{2}}\\\\&\Rightarrow&AC=\sqrt{6^{2}-3^{2}}\\ \\&\Rightarrow&AC=\sqrt{36-9}\\ \\&\Rightarrow&AC=\sqrt{27}\\\\&\Rightarrow&AC=\sqrt{9\times 3}\\\\&\Rightarrow&AC=3\sqrt{3}\end{array}$

D'où,

$\boxed{AC=3\sqrt{3}\;cm}$

3) La droite

$(AC)$ coupe le

$(\mathcal{C}')$ en

$E.$

a) Le triangle

$AEF$ est rectangle en

$E.$

En effet, on constate que

$AEF$ est un triangle inscrit dans le cercle

$(\mathcal{C}')$ et dont le côté

$[AF]$ est un diamètre de ce cercle.

Par conséquent,

$AEF$ est un triangle rectangle en

$E.$

Démontrons que

$(BC)\parallel (EF).$

En effet,

$ABC$ étant rectangle en

$C$ alors,

$(BC)$ est perpendiculaire à

$(AC).$

De même, comme

$AEF$ est rectangle en

$E$ alors, les droites

$(EF)\$ et

$\ (AC)$ sont perpendiculaires.

Ainsi,

$(BC)\$ et

$\ (EF)$ sont deux droites perpendiculaires à la droite

$(AC).$

Or, on sait que deux droites perpendiculaires à une même droite sont parallèles.

Par conséquent, les droites

$(BC)\$ et

$\ (EF)$ sont parallèles.

b) Calculons les longueurs

$AE\$ et

$\ EF.$

$-\$ Calcul de

$AE$

Les droites

$(BC)\$ et

$\ (EF)$ étant parallèles alors, les triangles

$ABC\$ et

$\ AEF$ sont en position de Thalès.

Ainsi, en utilisant le théorème de Thalès, on a :

$\dfrac{AE}{AC}=\dfrac{FA}{AB}$

Alors, en remplaçant

$AC\;,\ FA\$ et

$\ AB$ par leur valeur, on obtient :

$\begin{array}{rcl}\dfrac{AE}{3\sqrt{3}}=\dfrac{4}{6}&\Leftrightarrow&6\times AE=4\times 3\sqrt{3}\\\\&\Leftrightarrow&AE=\dfrac{12\sqrt{3}}{6}\\\\&\Leftrightarrow&AE=2\sqrt{3}\end{array}$

D'où,

$\boxed{AE=2\sqrt{3}\;cm}$

$-\$ Calcul de

$EF$

En appliquant encore le théorème de Thalès, on a :

$\dfrac{EF}{BC}=\dfrac{FA}{AB}$

Alors, en remplaçant

$BC\;,\ FA\$ et

$\ AB$ par leur valeur, on obtient :

$\begin{array}{rcl}\dfrac{EF}{3}=\dfrac{4}{6}&\Leftrightarrow&6\times EF=4\times 3\\\\&\Leftrightarrow&EF=\dfrac{12}{6}\\\\&\Leftrightarrow&EF=2\end{array}$

D'où,

$\boxed{EF=2\;cm}$

Exercice 25

1) Construisons un triangle

$IJK$ rectangle en

$I$ tel que :

$IJ=4.5\;cm\$ et

$\ IK=6\;cm.$

2) Calculons

$JK.$

Comme

$IJK$ est un triangle rectangle en

$I$ alors, en appliquant le théorème de Pythagore, on a :

$JK^{2}=IJ^{2}+IK^{2}$

Ainsi,

$\begin{array}{rcl} JK^{2}=IJ^{2}+IK^{2}&\Rightarrow&JK=\sqrt{IJ^{2}+IK^{2}}\\\\&\Rightarrow&JK=\sqrt{(4.5)^{2}+6^{2}}\\ \\&\Rightarrow&JK=\sqrt{20.25+36}\\ \\&\Rightarrow&JK=\sqrt{56.25}\\\\&\Rightarrow&JK=7.5\end{array}$

D'où,

$\boxed{JK=7.5\;cm}$

3) Plaçons le point

$P\in[IJ]$ tel que

$JP=3\;cm$ , puis traçons la parallèle à

$(IK)$ passant par

$P$ qui coupe

$(JK)$ en

$L.$

4) Calculons les distances

$JL\$ et

$\ PL.$

$-\$ Calcul de

$JL$

Les droites

$(IK)\$ et

$\ (PL)$ étant parallèles alors, les triangles

$IJK\$ et

$\ JPL$ sont en position de Thalès.

Ainsi, en appliquant le théorème de Thalès, on a :

$\dfrac{JL}{JK}=\dfrac{JP}{IJ}$

Alors, en remplaçant

$JK\;,\ JP\$ et

$\ IJ$ par leur valeur, on obtient :

$\begin{array}{rcl}\dfrac{JL}{7.5}=\dfrac{3}{4.5}&\Leftrightarrow&4.5\times JL=3\times 7.5\\\\&\Leftrightarrow&JL=\dfrac{22.5}{4.5}\\\\&\Leftrightarrow&JL=5\end{array}$

D'où,

$\boxed{JL=5\;cm}$

$-\$ Calcul de

$PL$

En appliquant encore le théorème de Thalès, on a :

$\dfrac{PL}{IK}=\dfrac{JP}{IJ}$

Alors, en remplaçant

$IK\;,\ JP\$ et

$\ IJ$ par leur valeur, on obtient :

$\begin{array}{rcl}\dfrac{PL}{6}=\dfrac{3}{4.5}&\Leftrightarrow&4.5\times PL=3\times 6\\\\&\Leftrightarrow&PL=\dfrac{18}{4.5}\\\\&\Leftrightarrow&PL=4\end{array}$

D'où,

$\boxed{PL=4\;cm}$

5) Soit

$A_{1}$ l'aire du triangle

$IJK$ et

$A_{2}$ celle du triangle

$JPL.$

Montrons que

$\dfrac{A_{2}}{A_{1}}=\left(\dfrac{JI}{JP}\right)^{2}.$

En effet, le triangle

$IJK$ étant un agrandissement du triangle

$JPL$ alors, le coefficient d'agrandissement des longueurs peut être donné par :

$m=\dfrac{JI}{JP}$

Par suite, le coefficient d'agrandissement des aires est :

$m^{2}=\left(\dfrac{JI}{JP}\right)^{2}$

Ainsi,

$A_{2}=m^{2}\times A_{1}$

Ce qui donne :

$\dfrac{A_{2}}{A_{1}}=m^{2}=\left(\dfrac{JI}{JP}\right)^{2}.$

D'où,

$\boxed{\dfrac{A_{2}}{A_{1}}=\left(\dfrac{JI}{JP}\right)^{2}}$

6) Construisons sur

$[JI)$ , le point

$A$ tel que

$JA=6\;cm$ puis sur

$[KI)$ le point

$B$ tel que

$IB=2\;cm\$ et

$\ B\in[KI].$

7) Démontrons que les droites

$(PB)\$ et

$\ (KJ)$ sont parallèles.

En effet,

$I\;,\ P\;,\ J$ sont trois points alignés d'une part, et

$I\;,\ B\;,\ K$ sont trois points alignés d'autre part, dans le même ordre.

En calculant les rapports

$\dfrac{IP}{IJ}\$ et

$\ \dfrac{IB}{IK}$ , on a :

$\dfrac{IP}{IJ}=\dfrac{IJ-JP}{IJ}=\dfrac{4.5-3}{4.5}=\dfrac{1.5}{4.5}=\dfrac{1}{3}$

$\dfrac{IB}{IK}=\dfrac{2}{6}=\dfrac{1}{3}$

On constate alors que :

$\dfrac{IP}{IJ}=\dfrac{IB}{IK}$

Par conséquent, d'après la réciproque du théorème de Thalès, les droites

$(PB)\$ et

$\ (KJ)$ sont parallèles.

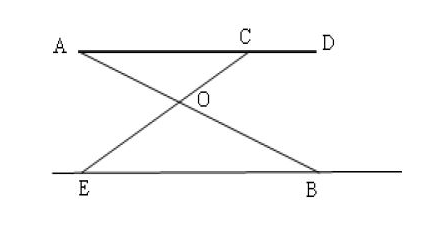
Exercice 26

La figure ci-dessous donne le schéma d'une table à repasser.

Le segment

$[AD]$ représente la planche.

Les segments

$[AB]\$ et

$\ [EC]$ représentent les pieds.

Les droites

$(AB)\$ et

$\ (EC)$ se coupent en

$O.$

On donne :

$AD=125\;cm$ ;

$AC=100\;cm$ ;

$OA=60\;cm$ ;

$OB=72\;cm$ ;

$OE=60\;cm$ ;

$OC=50\;cm.$

1) Montrons que la droite

$(AC)$ est parallèle à

$(EB).$

On a :

$A\;,\ O\;,\ B$ sont trois points alignés d'une part, et

$C\;,\ O\;,\ E$ sont trois points alignés d'autre part, dans le même ordre.

En calculant les rapports

$\dfrac{OC}{OE}\$ et

$\ \dfrac{OA}{OB}$ , on a :

$\dfrac{OC}{OE}=\dfrac{50}{60}=\dfrac{5}{6}$

$\dfrac{OA}{OB}=\dfrac{60}{72}=\dfrac{5}{6}$

On remarque alors que :

$\dfrac{OC}{OE}=\dfrac{OA}{OB}$

Par conséquent, d'après la réciproque du théorème de Thalès, la droite

$(AC)$ est parallèle à la droite

$(EB).$

2) Calculons l'écartement

$EB\$ en

$cm.$

En effet, comme les droites

$(AC)\$ et

$\ (EB)$ sont parallèles alors, les triangles

$EOB\$ et

$\ AOC$ sont en position de Thalès.

Ainsi, en appliquant le théorème de Thalès, on a :

$\dfrac{EB}{AC}=\dfrac{OB}{OA}$

Alors, en remplaçant

$AC\;,\ OA\$ et

$\ OB$ par leur valeur, on obtient :

$\begin{array}{rcl}\dfrac{EB}{100}=\dfrac{72}{60}&\Leftrightarrow&60\times EB=72\times 100\\\\&\Leftrightarrow&EB=\dfrac{7\,200}{60}\\\\&\Leftrightarrow&EB=120\end{array}$

D'où,

$\boxed{EB=120\;cm}$

3) Le triangle

$EOB$ n'est pas rectangle.

Justifions notre réponse.

On a :

$EB^{2}=120^{2}=14\,400$

$OB^{2}=72^{2}=5\,184$

$OE^{2}=60^{2}=3\,600$

Alors,

$OB^{2}+OE^{2}=5\,184+3\,600=8\,784$

On constate que

$EB^{2}$ n'est pas égal à

$OB^{2}+OE^{2}.$

Donc, le théorème de Pythagore n'est pas vérifié.

Par conséquent, le triangle

$EOB$ n'est pas rectangle.

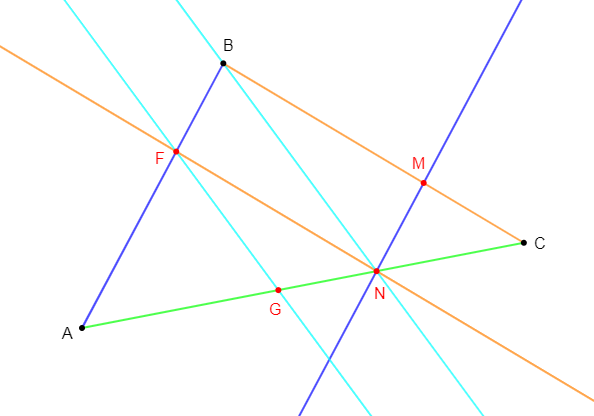
Exercice 27

1) Construisons le triangle

$ABC$ tel que :

$AB=6\;cm$ ;

$AC=9\;cm$ ;

$BC=7\;cm.$

2) Construisons le point

$M$ de

$[BC]$ tel que :

$BM=\dfrac{2}{3}BC.$

3) La parallèle à

$(AB)$ passant par

$M$ coupe

$(AC)$ en

$N.$

a) Démontrons que

$\dfrac{CN}{AC}=\dfrac{1}{3}$

Comme les droites

$(AB)\$ et

$\ (MN)$ sont parallèles alors, les triangles

$ABC\$ et

$\ CMN$ sont en position de Thalès.

Ainsi, en utilisant le théorème de Thalès, on a :

$\dfrac{CN}{AC}=\dfrac{CM}{BC}$

Or, on sait que :

$CM=BC-BM$

Comme

$BM=\dfrac{2}{3}BC$ alors, on a :

$\begin{array}{rcl} CM&=&BC-\dfrac{2}{3}BC\\\\&=&\left(1-\dfrac{2}{3}\right)BC\\\\&=&\dfrac{3-2}{3}BC\\\\&=&\dfrac{1}{3}BC\end{array}$

Donc,

$CM=\dfrac{1}{3}BC$

Ainsi, en remplaçant

$AC\;,\ CM\$ et

$\ BC$ par leur valeur, on obtient :

$\begin{array}{rcl}\dfrac{CN}{AC}=\dfrac{CM}{BC}&\Leftrightarrow&\dfrac{CN}{AC}=\dfrac{\dfrac{1}{3}BC}{BC}\\\\&\Leftrightarrow&\dfrac{CN}{AC}=\dfrac{BC}{3\times BC}\\\\&\Leftrightarrow&\dfrac{CN}{AC}=\dfrac{1}{3}\end{array}$

D'où,

$\boxed{\dfrac{CN}{AC}=\dfrac{1}{3}}$

b) Calculons

$NC.$

D'après le résultat de la question

$a)$ , on a :

$\dfrac{CN}{AC}=\dfrac{1}{3}.$

Ce qui donne alors :

$CN=\dfrac{1}{3}AC$

Ainsi, en remplaçant

$AC$ par sa valeur, on trouve :

$CN=\dfrac{1}{3}\times 9=\dfrac{9}{3}=3$

D'où,

$\boxed{NC=3\;cm}$

4) Calculons

$MN.$

En effet, comme les triangles

$ABC\$ et

$\ CMN$ sont en position de Thalès alors, le coefficient

$k$ de réduction des longueurs est :

$k=\dfrac{CN}{AC}=\dfrac{1}{3}$

Donc, pour trouver la longueur d'un côté du triangle

$CMN$ , on multiplie par

$\dfrac{1}{3}$ la longueur du côté correspondant du triangle

$ABC.$

Ainsi,

$MN=\dfrac{1}{3}AB=\dfrac{6}{3}=2$

D'où,

$\boxed{MN=2\;cm}$

5) La parallèle à

$(BC)$ passant par

$N$ coupe

$(AB)$ en

$F.$

La parallèle à

$(BN)$ passant par

$F$ coupe

$(AC)$ en

$G.$

Démontrons que :

$AN^{2}=AC\times AG.$

En effet, les droites

$(BC)\$ et

$\ (FN)$ étant parallèles alors, les triangles

$ABC\$ et

$\ AFN$ sont en position de Thalès.

Donc, en appliquant le théorème de Thalès, on a :

$\dfrac{AN}{AC}=\dfrac{AF}{AB}\quad(1)$

De la même manière, les droites

$(BN)\$ et

$\ (FG)$ étant parallèles alors, les triangles

$ABN\$ et

$\ AFG$ sont en position de Thalès.

Ainsi, d'après le théorème de Thalès, on a :

$\dfrac{AG}{AN}=\dfrac{AF}{AB}\quad(2)$

En comparant les égalités

$(1)\$ et

$\ (2)$ , on peut alors écrire :

$\dfrac{AN}{AC}=\dfrac{AG}{AN}$

Par suite,

$\begin{array}{rcl}\dfrac{AN}{AC}=\dfrac{AG}{AN}&\Leftrightarrow&AN\times AN=AC\times AG\\\\&\Leftrightarrow&AN^{2}=AC\times AG\end{array}$

D'où,

$\boxed{AN^{2}=AC\times AG}$

Auteur:

Diny Faye

Commentaires

Abdou mbodj (non vérifié)

mar, 12/03/2019 - 14:02

Permalien

Maths 3e

Le reste de la correction des exercices

répondre

Mareme diop (non vérifié)

ven, 01/22/2021 - 20:49

Permalien

Comprendre

Voir la correction des exercices pour en servit

répondre

Anonyme (non vérifié)

sam, 06/13/2020 - 20:18

Permalien

pdf

répondre

Anonyme (non vérifié)

sam, 10/03/2020 - 00:51

Permalien

Il faut corriger tout les

Il faut corriger tout les exercices je suis un peu satisfaite

répondre

Elhadj Amadou Gueye (non vérifié)

jeu, 06/17/2021 - 18:23

Permalien

Remerciements

Vous avez fait un travail remarquable cependant la seule chose que je déplore est qu'il n y a pas de correction pour tous les exercices mais merci quand meme

répondre

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Solution des exercices : Théorème de Thalès - 3e

Formulaire de recherche

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Exercice 5

Exercice 6

Exercice 7

Exercice 8

Exercice 9

Exercice 10

Exercice 11

Exercice 12

Exercice 13

Exercice 14

Exercice 15

Exercice 16

Exercice 17

Exercice 18

Exercice 19

Exercice 20

Exercice 22

Exercice 23

Exercice 24

Exercice 25

Exercice 26

Exercice 27

Commentaires

Maths 3e

Comprendre

pdf

Il faut corriger tout les

Remerciements

Ajouter un commentaire

Plain text