Corrigé BFEM Maths 2019 2ième groupe
Exercice 1
1) Deux nombres $m$ et $n$ sont dits inverses lorsque leur produit est égal à 1 :
$m\times n=1.$
Dans ce cas, chacun de ces nombres est l'inverse de l'autre.
On a à la fois $m=\dfrac{1}{n}$ et $n=\dfrac{1}{m}.$
$1^{er}$ méthode
Le numérateur de $x$, $2+\dfrac{3}{4}$, s'écrit, en réduisant au même dénominateur :
$\dfrac{2\times4+3}{4}=\dfrac{8+3}{4}=\dfrac{11}{4}.$
Par conséquent, le nombre $x=\dfrac{2+\dfrac{3}{4}}{5}$ est égal à $\dfrac{\dfrac{11}{4}}{5}=\dfrac{11}{4}\times\dfrac{1}{5}=\dfrac{11}{20}$ et par suite, son inverse vaut $\dfrac{20}{11}.$
$2^{ième}$ méthode
L'inverse de $x$ est $\dfrac{5}{2+\dfrac{3}{4}}=\dfrac{5}{\left(\dfrac{11}{4}\right)}=5\times\dfrac{4}{11}=\dfrac{5\times4}{11}=\dfrac{20}{11}.$
Ce nombre est bien de la forme $\dfrac{p}{q}$ avec $p=20$ et $q=11.$
2) On multiplie le numérateur et le dénominateur de $a$ par l'expression conjuguée du dénominateur de $a$ qui est $2\sqrt{3}+2.$
On obtient ainsi
$\begin{array}{rcl} a&=&\dfrac{(2-\sqrt{3})(2\sqrt{3}+2)}{(2\sqrt{3}-2)(2\sqrt{3}+2)}\\ \\&=&\dfrac{4\sqrt{3}+4-2\times 3-2\sqrt{3}}{(2\sqrt{3})^{2}-4}\\ \\&=&\dfrac{2\sqrt{3}-2}{8}\\ \\&=&\dfrac{\sqrt{3}-1}{4}\end{array}$
3) Calculons d'abord $(a+1).$
On a d'après la question précédente :
$$a+1=\dfrac{\sqrt{3}-1}{4}+1=\dfrac{\sqrt{3}-1+4}{4}=\dfrac{\sqrt{3}-1}{4}.$$
L'inverse de $(a+1)$ est alors égal à
$\begin{array}{rcl}\dfrac{4}{\sqrt{3}+3}&=&\dfrac{4}{3+\sqrt{3}}\\ \\&=&\dfrac{4(3-\sqrt{3})}{(3+\sqrt{3})(3-\sqrt{3})}\\ \\&=&\dfrac{4(3-\sqrt{3})}{3^{2}-(\sqrt{3})^{2}}\\ \\&=&\dfrac{4(3-\sqrt{3})}{9-3}\\ \\&=&\dfrac{4(3-\sqrt{3})}{6}\\ \\&=&\dfrac{2}{3}\times(3-\sqrt{3})\end{array}$
4) L'inégalité $1.732<\sqrt{3}<1.733$ est équivalente, en ajoutant $-1$ aux $3$ membres, à $$0.732<\sqrt{3}-1<0.733$$ puis en divisant les trois membres par $4$ qui est positif, on obtient :
$$\dfrac{0.732}{4}<\dfrac{\sqrt{3}-1}{4}<\dfrac{0.733}{4}.$$
La machine donne les approximations suivantes :
$\dfrac{0.732}{4}\cong 0.183$ et $\dfrac{0.733}{4}\cong 0.18325$
Ainsi on a $0.18<a<0.19$ qui est bien un encadrement de $a$ à $10^{-2}$ près.
Exercice 2
1) Seuls les ensembles $S_{4}$ et $S_{5}$ peuvent éventuellement convenir, car les solutions d'un système sont nécessairement des couples.
Si $x=1\ $ et $\ y=2$, la première équation du système est vérifiée car $3\times1-2-1=0$ et la seconde aussi car $1-2\times2+3=0.$
Si $x=2\ $ et $\ y=1$, la première équation du système n'est pas vérifiée car $3\times2-1-1=4\neq 0$
On en conclut finalement que $S_{4}$ est l'ensemble des solutions du système.
2) a) Quand le garçon avait l'âge de sa sœur, il était âgé de $y$ années.
C'était donc il y a $x-y$ années (son âge actuel moins son âge d'alors).
Comme les deux enfants grandissent en même temps, l'âge de la sœur était alors $y-(x-y)=2y-x$ années.
b) Puisque l'âge actuel du garçon est le double de l'âge de sa sœur à l'époque, on a :
$$x=2(2y-x)$$
Soit :
$\begin{array}{rcrcl} x=4y-2x&\Rightarrow&3x&=&4y\\ \\&\Rightarrow&x&=&\dfrac{4}{3}y\end{array}$
3) Compte tenu de l'hypothèse et des résultats précédents, les âges actuels $x\ $ et $\ y$ des deux enfants vérifient le système $$\left\lbrace\begin{array}{lcl} x+y&=&42\\ \\ x&=&\dfrac{4}{3}y \end{array}\right.$$
On peut résoudre ce système par la méthode de substitution, puisque $x$ est déjà exprimé en fonction de $y.$
On a alors :
$\dfrac{4}{3}y+y=42$, soit $\dfrac{7}{3}y=42$, d'où $y=3\times\dfrac{42}{7}=3\times 6=18$ et par suite, $x=\dfrac{4}{3}\times 18=4\times 6=24.$
On conclut que le garçon a actuellement $24$ ans et la fille $18$ ans.
Vérification :
Quand le garçon avait l'âge de sa sœur, c'est-à-dire $18$ ans, c'était il y a $(24-18)=6$ ans.
La fille avait alors $18-6=12$ ans et l'âge actuel du garçon, $24$ ans est bien le double de cet âge.
Exercice 3
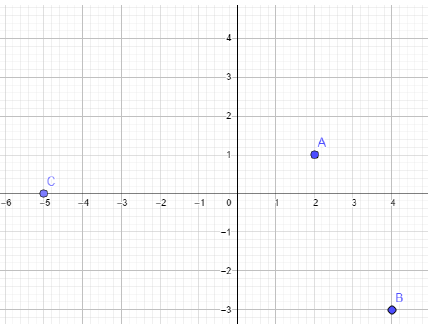
1) Voir figure ci-dessous
2) D'après une propriété du Cours, les coordonnées de $I$ sont les demi-sommes des abscisses et des ordonnées des points $A$ et $C$ : $I\begin{pmatrix} \dfrac{x_{A}+x_{C}}{2}\\ \dfrac{y_{A}+y_{C}}{2} \end{pmatrix}$, soit $I\begin{pmatrix} \dfrac{2+0}{2}\\ \dfrac{1-5}{2} \end{pmatrix}$ ou encore $I\begin{pmatrix} 1\\ -2 \end{pmatrix}.$
3) $1^{er}$ méthode
Puisque $I$ est le milieu de $[AC]$, et par conséquent, le centre du cercle $(\mathcal{C})$ de diamètre $[AC]$, le rayon de ce cercle est égale à la distance $IC$ ou mieux encore à la moitié de la distance $AC.$
Or, on a :
$\begin{array}{rcl} AC&=&\sqrt{(x_{C}-x_{A})^{2}+(y_{C}-y_{A})^{2}}\\ \\&=&\sqrt{(0-2)^{2}+(-5-1)^{2}}\\ \\&=&\sqrt{4+36}\\ \\&=&\sqrt{40}\\ \\&=&2\sqrt{10}\end{array}$
Donc le rayon de ce cercle est égal à $\sqrt{10}.$
Pour justifier que $B$ est un point du cercle $(\mathcal{C})$, il suffit de montrer que la distance $IB$ est égal à $\sqrt{10}.$
Or, d'après les données de l'énoncé et les coordonnées de $I$ calculées précédemment, on a :
$\begin{array}{rcl} IB&=&\sqrt{(x_{B}-x_{I})^{2}+(y_{B}-y_{I})^{2}}\\ \\&=&\sqrt{(4-1)^{2}+(-3+2)^{2}}\\ \\&=&\sqrt{9+1}\\ \\&=&\sqrt{10}\end{array}$
D'où le résultat.
$2^{ième}$ méthode
Montrer que les droites $(BC)$ et $(BA)$ sont perpendiculaires, ou, ce qui revient au même, que les vecteurs $\overrightarrow{BC}$ et $\overrightarrow{BA}$ sont orthogonaux.
Or, $\overrightarrow{BC}$ a pour coordonnées $\begin{pmatrix} x_{C}&-x_{C}\\ y_{C}&-y_{B} \end{pmatrix}$, soit $\overrightarrow{BC}\begin{pmatrix} 0&-4\\ -5&-(-3) \end{pmatrix}$ ou encore $\overrightarrow{BC}\begin{pmatrix} -4\\ -2 \end{pmatrix}$, et $\overrightarrow{BA}$ a pour coordonnées $\begin{pmatrix} x_{A}&-x_{B}\\ y_{A}&-y_{B} \end{pmatrix}$, soit $\overrightarrow{BA}\begin{pmatrix} 2&-4\\ 1&-(3) \end{pmatrix}$ ou encore $\overrightarrow{BA}\begin{pmatrix} -2\\ 4 \end{pmatrix}.$
La condition d'orthogonalité s'écrit :
$$x_{\overrightarrow{BC}}\cdot x_{\overrightarrow{BA}}+y_{\overrightarrow{BC}}\cdot y_{\overrightarrow{BA}}=0$$
ou encore : $-4\times (-2)+(-2)\times 4=8-8=0$, ce qui est bien vrai.
Il suffit alors d'utiliser la propriété classique :
« Tout point $M$ tel que les droites $(MA)$ et $(MB)$ soient perpendiculaires est situé sut le cercle de diamètre $[AB].$
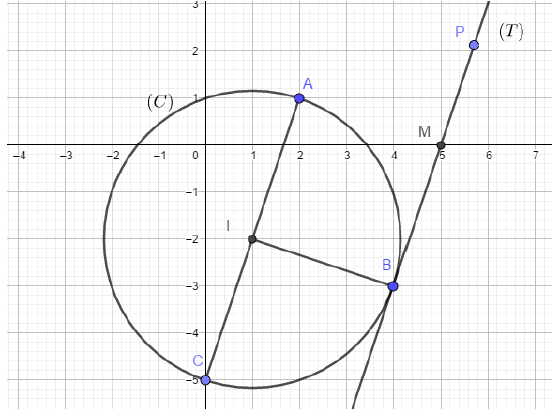
4) $(\mathcal{T})$ est, par définition d'une tangente en un point à un cercle, la perpendiculaire en $B$ à la droite $(IB).$
Un point $P$ de coordonnées $(x\;,\ y)$ est situé sur $(\mathcal{T})$ si et seulement si les vecteurs $\overrightarrow{BP}$ et $\overrightarrow{BI}$ sont orthogonaux, (voir figure ci-dessous), ce qui se traduit par la condition :
$$x_{\overrightarrow{BP}}\cdot x_{\overrightarrow{BI}}+y_{\overrightarrow{BP}}\cdot y_{\overrightarrow{BI}}=0$$
Or, $\overrightarrow{BP}$ a pour coordonnées $\begin{pmatrix} x&-x_{B}\\ y&-y_{B} \end{pmatrix}$, soit $\overrightarrow{BP}\begin{pmatrix} x&-4\\ y&-(-3) \end{pmatrix}$ ou encore $\overrightarrow{BP}\begin{pmatrix} x&-4\\ y&+3 \end{pmatrix}$ et $\overrightarrow{BI}$ a pour coordonnées $\begin{pmatrix} x_{I}&-x_{B}\\ y_{I}&-y_{B} \end{pmatrix}$, soit $\overrightarrow{BI}\begin{pmatrix} 1&-4\\ -2&-(-3) \end{pmatrix}$ ou encore $\overrightarrow{BI}\begin{pmatrix} -3\\ 1 \end{pmatrix}.$
La condition d'orthogonalité s'écrit donc :
$-3(x-4)+1\times(y+3)=0$, soit après simplification : $-3x+y+15=0.$
5) Le point $M$, étant situé sur l'axe des abscisses, a pour ordonnée $0$ et son abscisse $x_{M}$ doit vérifier l'équation précédente, d'où :
$-3x_{M}+0+15=0$, ce qui entraîne que $x_{M}=5.$
Il en résulte que le point $M$ a pour coordonnées $(5\;;\ 0).$
Exercice 3 (7 points)
1) Dans un repère orthonormal $(O\;,\ \vec{i}\;,\ \vec{j})$, construis les points $A(2\;;\ 1)$, $B(4\;;\ -3)$, et $C(0\;;\ -5).$
2) Détermine les coordonnées du milieu $I$ de $[AC].$
3) Justifie que le point $B$ appartient au cercle $(\mathcal{C})$ de diamètre $[AC].$
4) Détermine l'équation de la tangente $(\mathcal{T})$ au cercle $(\mathcal{C})$ en $B.$
Détermine les coordonnées du point $M$ intersection de la droite $(\mathcal{T})$ avec l'axe des abscisses.

Commentaires
Anonyme (non vérifié)
mer, 08/26/2020 - 21:37
Permalien
EXCELLENT
Babacar Niang (non vérifié)
mer, 12/23/2020 - 12:50
Permalien
Salut Mr comment vous allez
Ibrahim Kalil bah (non vérifié)
dim, 07/04/2021 - 23:02
Permalien
Je voulais anglais bfem
Ajouter un commentaire