Introduction à la géométrie - 6e
Classe:
Sixième
I. Observation de l'espace
I.1. Le Parallélépipède rectangle ou Le Pavé droit
Le parallélépipède rectangle est un polyèdre qui a :
$-\ $ Six faces rectangulaires (parallélogrammes) dont les faces opposées sont égales et parallèles deux à deux
$-\ $ Douze arêtes égales deux à deux
$-\ $ Huit sommets
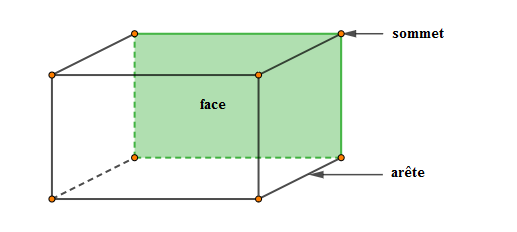
Exemples : boites d'allumettes, boite de savon, boite de patte dentifrice, morceau de sucre
I.2. Le Cube
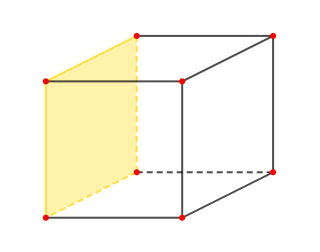
Le cube est un parallélépipède rectangle à :
$-\ $ Six faces carrées et égales
$-\ $ Douze arêtes de même longueur
$-\ $ Huit sommets
I.3. Le Cylindre
Le cylindre est un solide limité par une surface cylindrique et deux disques circulaires et parallèles
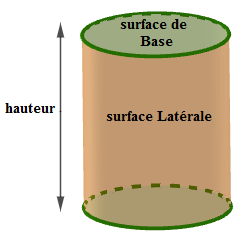
Exemples : pot de gloria, pot de tomates
I.4. La Sphère
La sphère est une surface fermée dont tous les points sont à la même distance (rayon) d'un point intérieur appelé centre.
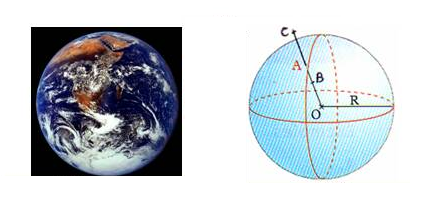
Exemples : globe terrestre, boule bulle de savon, goutte d'eau
Une balle de ping-pong est une sphère de centre $O$ et de rayon $2\;cm.$ Tous les points qui lui appartiennent se trouvent à $2\;cm$ de $O.$
La Terre est une boule de centre $O$ et de rayon $6\,370\;km.$ Tous les points qui lui appartiennent se trouvent à moins de $6\,370\;km$ de $O.$
Aire de la sphère : $\mathcal{A}=4\pi r^{2}$
Exemple : Surface terrestre
$\mathcal{A}=4\times\pi\times 6\,370^{2}$
$\mathcal{A}\approx 509\,904\,364\;Km^{2}\approx 5.1\;10^{8}\;Km^{2}$
Volume de la boule : $\mathcal{V}=\dfrac{4}{3}\pi r^{3}$
Exemple : Volume de la terre
$\mathcal{V}=\dfrac{4}{3}\pi r^{3}=\dfrac{4\times\pi\times 6\,370^{3}}{3}$
$\mathcal{V}\approx 1\,082\,696\,932\,430\;Km^{3}\approx 1.1\;10^{12}$
II. Plan et point
Le tableau, la surface d'une feuille de cahier, celle de l'ardoise ou table matérialisent un plan : ce sont des réductions d'un plan ou partie d'un plan.
Lorsqu'on pose la pointe du stylo sur la feuille; celle-ci laisse une trace appelée un point.
Le plan est illimité et formé d'un ensemble infini de points. Le point est donc un élément du plan.
Activité
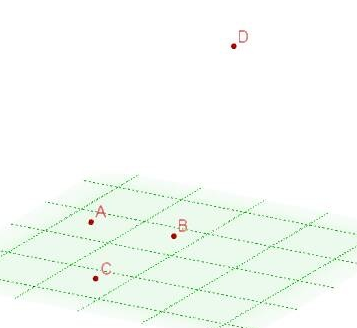
Soit le plan nommé $(\mathcal{P}).$ Placer les points $A\;,\ B\;,\ C\ $ et $\ D$ tels que :
$$A\in(\mathcal{P})\;,\ B\in(\mathcal{P})\;,\ C\in(\mathcal{P})\;,\ D\notin(\mathcal{P})$$
Solution
III. Droites et points alignés
Activité
Soit $A$ un point du plan. Tracez une droite $(\mathcal{D})$ passant par ce point.
Marquez deux points $E\ $ et $\ F$ de part et d'autre de la droite $(\mathcal{D})$ puis un point $B$ sur cette même droite $(\mathcal{D}).$
1) Que peut-on dire des points $A\;,\ B\;,\ E\;,\ F$ par rapport à la droite $(\mathcal{D})\ ?$
2) Si le point $C$ appartient à $(\mathcal{D})$ comment sont les trois points $A\;,\ B$, et $C\ ?$
Solution
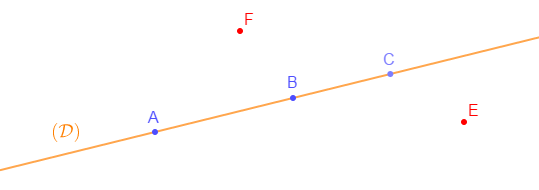
1) On peut dire que $A\ $ et $\ B$ appartiennent à la droite $(\mathcal{D})$ et que les points $E\ $ et $\ F$ n'appartiennent pas à $(\mathcal{D})$
2) Si le point $C$ appartient à $(\mathcal{D})$ alors, les trois points $A\;,\ B\ $, et $\ C$ sont alignés.
III.1. Définition et notation
Une droite est un ensemble de points alignés. Pour noter une droite; on utilise deux parenthèses entre lesquelles on met :
$-\ $ Une lettre en gros caractère ou en minuscule :
$$(D)\;,\ (L)\;,\ (\Delta)\;,\ (d)$$
$-\ $ Deux lettres en gros caractère dont chacun désigne un point fixe sur la droite :
$$(AB)\;,\ (EF)\;,\ (FG)\;,\ (XY)$$
$-\ $ Deux lettres en minuscules dont chacun désigne un point variable sur la droite :
$$(xy)\;,\ (xx')\;,\ (yy')$$
III.2. Propriétés
Activité 1
Marquez un point $A.$
Tracez toutes les droites possibles passant par le point $A.$
Que remarquez-vous ?
Solution
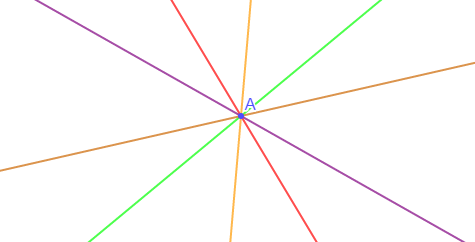
On remarque qu'il y a plusieurs droites qui passent par ce même point $A.$
Propriété 1
Par un point du plan, passe une infinité de droites.
Activité 2
Marquez deux points $A\ $ et $\ B.$
Tracez toutes les droites passant par $A\ $ et $\ B.$
Combien y en a-t-il ?
Solution
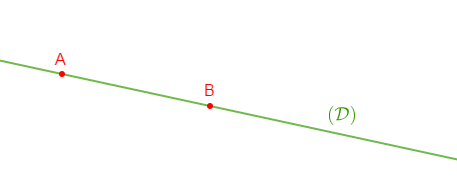
On constate qu'il y a une seule droite qui passe par $A\ $ et $\ B.$
Propriété 2
Par deux points du plan; passe une et une seule droite.
Remarque
$-\ $ Une droite peut être prolongée infiniment dans les deux cotés (sens) : on dit que la droite est illimitée.
$-\ $ Chaque droite partage le plan en deux demi-plans.
IV. Demi-droite et segment
IV.1. Demi-droite
Activité
Soit la droite $(\mathcal{D}).$
Placer sur $(\mathcal{D})$, les points $A\;,\ B\;,\ C\ $ et $\ D.$
Trouver le nombre de demi-droites sur cette droite. Nommer en deux demi-droites.
Solution
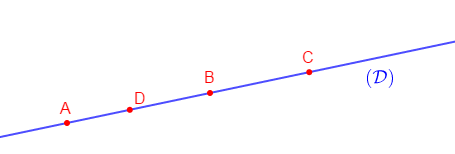
Définition
On appelle demi-droite; une portion de droite limitée en un point appelé origine et illimité de l'autre coté.
On note une demi-droite par deux points pris entre un crochet et une parenthèse.
Remarque
Soient $A\;,\ B\ $ et $\ C$ trois points dans cet ordre sur une droite.La demi-droite $[AB)\ $ et $\ [BC)$ ont la même origine et sont portées par la même droite.
On dit qu'elles sont opposées.
IV.2. Segment
Activité
Sur une droite $(\mathcal{D})$ du plan, marquer les points $E\;,\ F\;,\ G\;,\ H\ $ et $\ I$ dans cet ordre.
Déterminer tous les segments de la figure.
Solution

Définition
On appelle segments toute portion de droite limitée par deux points appelés extrémités.
Deux segments qui ont les mêmes extrémités sont égaux.
On note un segment par deux points entre deux crochets.
Remarque
Une demi-droite ou un segment sont toujours portés par une droite.
V. Position relative de deux droites
V.1. Droites sécantes
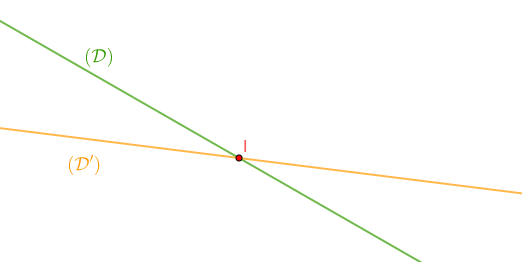
Deux droites sont sécantes lorsqu'elles se coupent en un point ; elles forment une intersection.
On dit que :
$-\ $ Les droites $(\mathcal{D})\ $ et $\ (\mathcal{D}')$ se coupent en $I$.
$-\ $ Les droites $(\mathcal{D})\ $ et $\ (\mathcal{D}')$ sont sécantes $I$.
$-\ $ Les droites $(\mathcal{D})\ $ et $\ (\mathcal{D}')$ sont concourantes en $I$.
$-\ $ L'intersection de $(\mathcal{D})\ $ et $\ (\mathcal{D}')$ est le point $I.$
On note :
$$(\mathcal{D})\cap(\mathcal{D}')=I$$
Deux droites sécantes partagent le plan en quatre parties appelées secteurs.
V.2. Droites disjointes
Deux droites sont disjointes sont deux droites qui n'ont aucun point commun.
Si $(\mathcal{D})\ $ et $\ (\mathcal{D}')$ sont disjointes on a :
$$(\mathcal{D})\cap(\mathcal{D}')=\{\emptyset\}$$
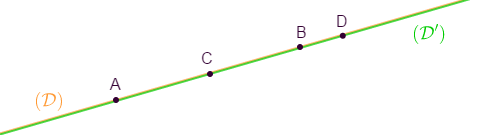
V.3. Droites confondues
Deux droites confondues ont tous leurs points communs.
VI. Mesure de longueurs de segments
VI.1. Longueur d'un segment
Activité
Soit le segment $[AB].$
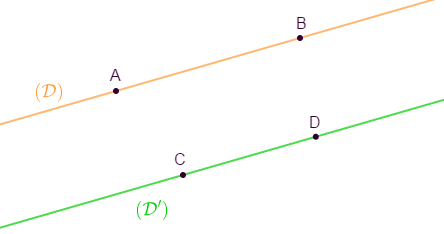
Construis le segment $[FG]$ de même longueur que $[AB]$ et de support $(\mathcal{D}).$
Sur $(\mathcal{D}')$, construis $[GH]$ de même longueur que $[FG].$
Solution
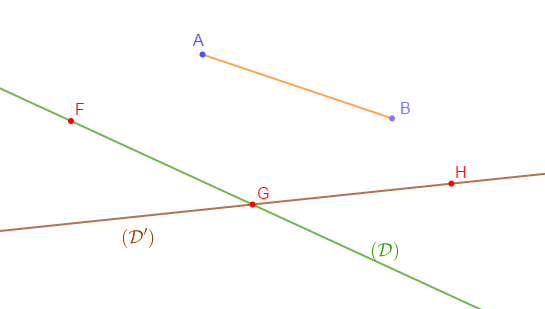
Définition
La mesure d'un segment ou la longueur d'un segment est la distance qui sépare les deux extrémités du segment.
Notation : La mesure d'un segment $[AB]$ est noté : $AB.$
Codage : Sur une figure, les segments de même longueur sont codés par un même signe ou symbole.
VI.2. Rapport de deux longueurs
Activité
Soient les segments : $[AB]\;,\ [CD]\ $ et $\ [EF].$
Comparer les mesures de ces trois segments pris deux à deux.
Solution
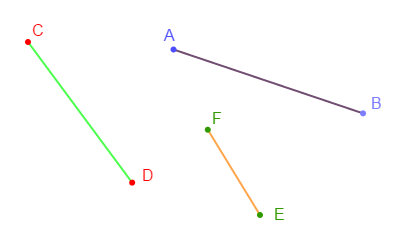
Avec une règle graduée, on a :
mesure de $[AB]$ égale $3\;cm$
mesure de $[CD]$ égale $2.5\;cm$
mesure de $[EF]$ égale $2\;cm$
Donc, $AB>CD\;,\ CD>EF\ $ et $\ AB>EF.$
VI.3. Milieu d'un segment
Activité
Trace un segment $[AB]$ de longueur $8\;cm.$
Plie la feuille suivant $(AB).$
Plie à nouveau la feuille pour que $A$ et $B$ coïncident.
Déplie la feuille; note $(D)$ la droite de pliage ne contenant pas $A$ et $B$, et $I$ le point commun à $(\mathcal{D})$ et $(AB).$
Que peut-on dire de $IA\ $ et $\ IB\ ?$
Définition
On appelle milieu d'un segment, le point de ce segment qui est égale distance de ses extrémités.
Construction
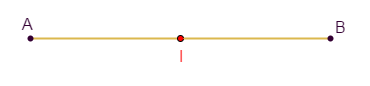
Traduction mathématique
$I$ est le milieu de $[AB]$ signifie que :
$$AI=IB$$
Remarque
Ne pas confondre :
$-\ \ (AB)$ qui est la droite passant par les points $A\ $ et $\ B$
$-\ \ [AB)$ qui est la demi-droite d'origine $A$ et passant par le point $B$
$-\ \ [AB]$ qui est le segment d'extrémités $A\ $ et $\ B$
$-\ \ AB$ qui est la distance entre les points $A\ $ et $\ B$
VII. Inégalité triangulaire
Activité
1) Trace un segment $[AB]$ de longueur $6\;cm.$
Marquer un point $M\in[AB]$ et utilise ta règle graduée pour comparer $AM+MB\ $ et $\ AB.$
2) Le résultat sera-t-il différent si tu choisissais d'autres points de $[AB]\ ?$
Donne une conclusion.
3) Marque un point $N\in(AB)$ et non à $[AB].$
Utilise ta règle graduée pour comparer $AN+NB\ $ et $\ AB$.
Solution
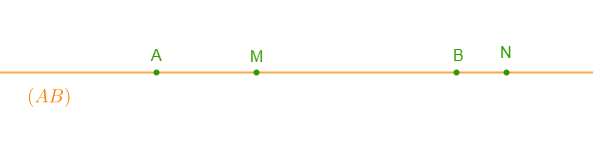
1) $AM=2\;cm\ $ et $\ MB=4\;cm$
Donc, $AM+MB=2\;cm+4\;cm=6\;cm$
D'où, $AM+MB=AB.$
2) Le résultat sera le même si on choisissait d'autres points de $[AB].$
Conclusion : Lorsque $M$ appartient au segment $[AB]$ alors, on a : $AM+MB=AB$
3) $AN=7\;cm\ $ et $\ NB=1\;cm$
Donc, $AN+NB=7\;cm+1\;cm=8\;cm$
D'où, $AN+NB>AB.$
Propriété 1
Si $M\in[AB]$ alors, on a :
$$AM+MB=AB$$
Exercice d'application
Soit $[AB]$ de mesure $5\;cm.$
Marquer $M\in[AB]$ tel que $MA=\;2cm.$
Déterminer $MB$
Solution
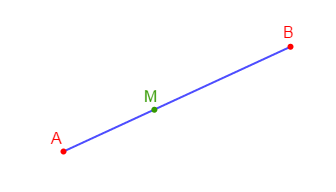
Comme $M\in[AB]$ alors, on a :
$$AM+MB=AB$$
Par suite, $MB=AB-AM$
D'où, $MB=5\;cm-2\;cm=3\;cm$
Propriété 2 (réciproque de la propriété 1)
Si $AM+MB=AB$ alors, $M\in[AB]$
Activité
trace un triangle $ABC$ et, sans mesurer, complète :
$$AC+CB\cdots AB\;,\quad AB+BC\cdots AC\;,\quad BA+AC\cdots BC$$
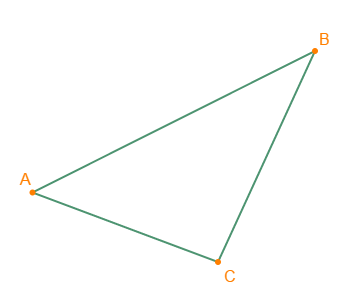
$$AC+CB>AB\;,\quad AB+BC>AC\;,\quad BA+AC>BC$$
Propriété 3
Si $M$ n'appartient pas à $[AB]$ alors, on a :
$$AM+MB>AB$$
Exercice d'application
Soit $ABC$ un triangle tel que $AB=2\;cm\;,\ BC=3\;cm\ $ et $\ AC=4\;cm.$
Montrer que $A$ n'appartient pas à $[BC]$
Solution
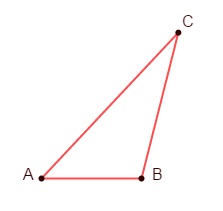
Calculons $BA+AC$
On a : $BA+AC=2\;cm+4\;cm=6\;cm$
Par suite, nous constatons que : $BA+AC>BC$
Ce qui montre que le point $A$ n'appartient pas au segment $[BC].$

Commentaires
Marie tening (non vérifié)
sam, 11/28/2020 - 21:17
Permalien
Deux segments qui ont les
fdini
dim, 11/29/2020 - 11:17
Permalien
un segment a deux extrémités
un segment a deux extrémités donc, si deux segments $[AB]$ et $[CD]$ ont les mêmes extrémités cela veut dire par exemple que $A=C$ et $B=D$ ou encore, $A=D$ et $B=C$ d'où $[AB]=[CD]$
En fait il ne faut pas confondre avec les extémités des vecteurs ; c'est différent
deux vecteurs peuvent avoir les mêmes extrémités sans être égaux
Mor Ndiaye sow (non vérifié)
lun, 04/05/2021 - 20:34
Permalien
si vous connaissez un
Anonyme (non vérifié)
mer, 05/19/2021 - 20:00
Permalien
<script>alert('Bienvenue !')<
Anonyme (non vérifié)
lun, 10/25/2021 - 11:38
Permalien
Je souhaiterais avoir le
Anonyme (non vérifié)
mar, 02/15/2022 - 01:10
Permalien
pdf
Anonyme (non vérifié)
mar, 02/15/2022 - 01:12
Permalien
puis-je avoir ce document
Anonyme (non vérifié)
ven, 07/14/2023 - 10:57
Permalien
bien
Wan- gbi dackis... (non vérifié)
mar, 12/10/2024 - 05:19
Permalien
Avoir des notions sur la géométrie de sixieme
Ajouter un commentaire