Solution des exercices : Multiplication des nombres décimaux arithmétiques - 6e
Classe:
Sixième
Exercice 1
1) Posons puis effectuons les produits suivants.
a) Soit $456\times 23$ ; en posant et en effectuant l'opération, on obtient :
$$\begin{array}{rl}&\quad 456\\\times&\quad \ 23\\ \hline &\ 1368\\+&\ 912.\\ \hline =&10488\end{array}$$
b) On a : $7.81\times 9.6$ donc, en posant et en effectuant l'opération, on obtient :
$$\begin{array}{rl}&\quad 7,81\\\times&\quad 9,6\\ \hline &\ \;4686\\+&\;7029.\\ \hline =&74,976\end{array}$$
2) Calculons mentalement
a) $23.45\times 1000=23\,450$
b) $0.01\times 308.2009=3.082009$
3) Donnons l'ordre de grandeur de chacun des produits.
Pour calculer l'ordre de grandeur (OG) d'un produit, on choisit d'abord une précision adaptée. Ensuite, on remplace chacun des facteurs par leur ordre de grandeur et enfin, on effectue le produit de ces ordres de grandeur
a) Calcul de l'OG de $305\times 98$
On choisit une précision à la centaine près et on obtient alors :
$305$ est proche de $300$
$98$ est proche de $100$
Donc, l'ordre de grandeur de $305\times 98$ est égal à $300\times 100=30\,000$
b) $15.8\times 7.3$
On choisit une précision à l'unité près. Ce qui donne :
$15.8$ est proche de $16$
$7.3$ est proche de $7$
Donc, l'ordre de grandeur de $15.8\times 7.3$ est égal à $16\times 7=112$
Exercice 2
1) Soient $p\ $ et $\ q$ deux nombres décimaux arithmétiques tels que : $p\times q=7.5$
a) Les nombres $p\ $ et $\ q$ sont appelés facteurs.
b) Le nombre $7.5$ est appelé produit des nombres $p\ $ et $\ q$
c) Trouvons les nombres $p\ $ et $\ q.$
Il y a plusieurs nombres décimaux arithmétiques $p\ $ et $\ q$ qui vérifient : $p\times q=7.5$
Par exemple :
$0.1\times 75=7.5$ donc, $p=0.1\ $ et $\ q=75$
$0.5\times 15=7.5$ donc, $p=0.5\ $ et $\ q=15$
$0.3\times 25=7.5$ donc, $p=0.3\ $ et $\ q=25$
$1.5\times 5=7.5$ donc, $p=1.5\ $ et $\ q=5$
Exercice 3
Calculons en ligne les expressions suivantes de manière performante en précisant les propriétés de la multiplication ainsi utilisées.
Soit $A=3.5\times 4\times 10\times 25$
Comme la multiplication est commutative alors, on peut changer l'ordre des deux facteurs sans modifier le résultat.
Donc, $A=3.5\times 10\times 4\times 25$
La multiplication étant associative alors, on a :
$\begin{array}{rcl} A&=&3.5\times 10\times(4\times 25)\\ \\&=&3.5\times 10\times 100\\ \\&=&(3.5\times 10)\times 100\\ \\&=&35\times 100\\ \\&=&3\,500\end{array}$
D'où, $\boxed{A=3\,500}$
Soit $B=5\times 3.5\times 10\times 2$
La multiplication étant commutative alors, $B$ peut encore s'écrire :
$B=3.5\times 10\times 5\times 2$
Comme la multiplication est associative alors, on a :
$\begin{array}{rcl} B&=&3.5\times 10\times(5\times 2)\\ \\&=&3.5\times 10\times 10\\ \\&=&(3.5\times 10)\times 10\\ \\&=&35\times 10\\ \\&=&350\end{array}$
Donc, $\boxed{B=350}$
Soit $C=38\times 5.7\times 3.4\times 0\times 9$
Comme $0$ est l'élément absorbant de la multiplication alors, tout nombre multiplié par $0$ a un produit nul.
D'où, $\boxed{C=0}$
Soit $D=125\times 10\times 4\times 0.75\times 100\times 1$
$1$ étant l'élément neutre de la multiplication donc, tout nombre multiplié par $1$ a un produit égal à ce nombre lui-même.
Par suite, $D=125\times 10\times 4\times 0.75\times 100$
Comme la multiplication est associative alors, on a :
$\begin{array}{rcl} D&=&125\times 10\times 4\times(0.75\times 100)\\ \\&=&125\times 10\times 4\times 75\\ \\&=&125\times 10\times(4\times 75)\\ \\&=&125\times 10\times 300\\ \\&=&125\times(10\times 300)\\ \\&=&125\times 3\,000\\ \\&=&125\times(3\times 1\,000)\\ \\&=&(125\times 3)\times 1\,000\\ \\&=&375\times 1\,000\\ \\&=&375\,000\end{array}$
Ainsi, $\boxed{D=375\,000}$
Soit $E=4\times 0.1\times 5\times 25$
La multiplication étant commutative alors, $E$ peut encore s'écrire :
$E=4\times 25\times 0.1\times 5$
Comme la multiplication est associative alors, on a :
$\begin{array}{rcl} E&=&(4\times 25)\times 0.1\times 5\\ \\&=&100\times 0.1\times 5\\ \\&=&(100\times 0.1)\times 5\\ \\&=&10\times 5\\ \\&=&50\end{array}$
Ainsi, $\boxed{E=50}$
Soit $F=4\times 0.01\times 25\times 100$
Comme la multiplication est commutative alors, on a :
$F=4\times 25\times 0.01\times 100$
La multiplication étant associative alors, on obtient :
$\begin{array}{rcl} F&=&4\times 25\times(0.01\times 100)\\ \\&=&4\times 25\times 1\\ \\&=&(4\times 25)\times 1\\ \\&=&100\times 1\end{array}$
Donc, $F=100\times 1$
Or, $1$ est l'élément neutre de la multiplication donc, $100\times 1=100$
D'où, $\boxed{F=100}$
Exercice 4
1) Complétons les pointillés par les décimaux qui conviennent.
$(7.5\times 2)\times 5=15\times 5=75$
$7.5\times (2\times 5)=7.5\times 10=75$
On retrouve l'associativité qui est une propriété de la multiplication.
2) Citons les autres propriétés de la multiplication.
$\centerdot\ $ la commutativité
$\centerdot\ $ la distributivité par rapport à l'addition et à la soustraction
$\centerdot\ $ l'élément neutre ; $1$
$\centerdot\ $ l'élément absorbant ; $0$
Exercice 5
Calculons de deux manières différentes chacune des expressions suivantes en précisant la propriété de la multiplication utilisée.
Soit $A=3.5\times (9.2+5.8)$
$1e$ méthode
On a :
$\begin{array}{rcl} A&=&3.5\times (9.2+5.8)\\\\&=&3.5\times 15\\\\&=&52.5\end{array}$
Donc, $\boxed{A=52.5}$
$2e$ méthode
Comme la multiplication est distributive par rapport à l'addition alors, on a :
$\begin{array}{rcl} A&=&3.5\times (9.2+5.8)\\\\&=&3.5\times 9.2+3.5\times 5.8\\\\&=&32.2+20.3\\\\&=&52.5\end{array}$
D'où, $\boxed{A=52.5}$
Soit $B=40\times 12$
En calculant on trouve : $40\times 12=480$
D'où, $\boxed{B=480}$
On peut aussi écrire : $12=10+2$
Alors, on remplace $12$ par $10+2$, dans l'écriture de $B.$
On obtient :
$$B=40\times (10+2)$$
Comme la multiplication est distributive par rapport à l'addition alors, on a :
$\begin{array}{rcl} B&=&40\times (10+2)\\\\&=&40\times 10+40\times 2\\\\&=&400+80\\\\&=&480\end{array}$
Donc, $\boxed{B=480}$
Soit $C=12\times (7-5.5)$
$1e$ méthode
On a :
$\begin{array}{rcl} C&=&12\times (7-5.5)\\\\&=&12\times 1.5\\\\&=&18\end{array}$
Donc, $\boxed{C=18}$
$2e$ méthode
Comme la multiplication est distributive par rapport à la soustraction alors, on a :
$\begin{array}{rcl} C&=&12\times (7-5.5)\\\\&=&12\times 7-12\times 5.5\\\\&=&84-66\\\\&=&18\end{array}$
D'où, $\boxed{C=18}$
Soit $D=40\times 8$
On a : $40\times 8=320$
Donc, $\boxed{D=320}$
On peut aussi écrire : $8=10-2$
Ainsi, en remplaçant $8$ par $10-2$, dans l'écriture de $D$, on obtient :
$$D=40\times (10-2)$$
Comme la multiplication est distributive par rapport à la soustraction alors, on a :
$\begin{array}{rcl} D&=&40\times (10-2)\\\\&=&40\times 10-40\times 2\\\\&=&400-80\\\\&=&320\end{array}$
D'où, $\boxed{D=320}$
Exercice 6
Calculons de deux manières différentes chacune des expressions suivantes.
Soit $A=141\times 60-140\times 60$
$1e$ méthode
On a :
$\begin{array}{rcl} A&=&141\times 60-140\times 60\\\\&=&8\,460-8\,400\\\\&=&60\end{array}$
D'où, $\boxed{A=60}$
$2e$ méthode
En utilisant la distributivité de la multiplication par rapport à la soustraction, on peut aussi écrire :
$$60\times (141-140)=141\times 60-140\times 60$$
Ainsi, on a :
$\begin{array}{rcl} A&=&141\times 60-140\times 60\\\\&=&60\times (141-140)\\\\&=&60\times 1\\\\&=&60\end{array}$
Donc, $\boxed{A=60}$
Soit $B=6.6\times 7+7\times 3.4$
$1e$ méthode
On a :
$\begin{array}{rcl} B&=&6.6\times 7+7\times 3.4\\\\&=&46.2+23.8\\\\&=&70\end{array}$
Alors, $\boxed{B=70}$
$2e$ méthode
En utilisant la distributivité de la multiplication par rapport à l'addition, on peut aussi écrire :
$$7\times (6.6+3.4)=6.6\times 7+7\times 3.4$$
On a alors :
$\begin{array}{rcl} B&=&6.6\times 7+7\times 3.4\\\\&=&7\times (6.6+3.4)\\\\&=&7\times 10\\\\&=&70\end{array}$
Donc, $\boxed{B=70}$
Soit $C=13.5\times 4-13.5\times 2.5$
$1e$ méthode
On a :
$\begin{array}{rcl} C&=&13.5\times 4-13.5\times 2.5\\\\&=&54-33.75\\\\&=&20.25\end{array}$
Donc, $\boxed{C=20.25}$
$2e$ méthode
En utilisant la distributivité de la multiplication par rapport à la soustraction, on peut aussi écrire :
$$13.5\times (4-2.5)=13.5\times 4-13.5\times 2.5$$
Ainsi, on a :
$\begin{array}{rcl} C&=&13.5\times 4-13.5\times 2.5\\\\&=&13.5\times (4-2.5)\\\\&=&13.5\times 1.5\\\\&=&20.25\end{array}$
D'où, $\boxed{C=20.25}$
Soit $D=12.1\times 4+7.9\times 7-12.1\times 3+7.9\times 3$
$1e$ méthode
On a :
$\begin{array}{rcl} D&=&12.1\times 4+7.9\times 7-12.1\times 3+7.9\times 3\\\\&=&48.4+55.3-36.3+23.7\\\\&=&48.4-36.3+55.3+23.7\\\\&=&(48.4-36.3)+(55.3+23.7)\\\\&=&12.1+79\\\\&=&91.1\end{array}$
Ainsi, $\boxed{D=91.1}$
$2e$ méthode
Comme l'ordre des termes ne modifie pas le résultat alors, on $D$ peut encore s'écrire :
$$D=12.1\times 4-12.1\times 3+7.9\times 7+7.9\times 3$$
En utilisant la distributivité de la multiplication par rapport à la soustraction et à l'addition, on peut aussi écrire :
$$12.1\times(4-3)=12.1\times 4-12.1\times 3$$
$$7.9\times(7+3)=7.9\times 7+7.9\times 3$$
Donc, en remplaçant, on obtient :
$\begin{array}{rcl} D&=&12.1\times 4-12.1\times 3+7.9\times 7+7.9\times 3\\\\&=&12.1\times(4-3)+7.9\times(7+3)\\\\&=&12.1\times 1+7.9\times 10\\\\&=&12.1+79\\\\&=&91.1\end{array}$
D'où, $\boxed{D=91.1}$
Exercice 7
1) Calculons les carrés des nombres suivants.
$7^{2}=7\times 7=49$
$12^{2}=12\times 12=144$
$100^{2}=100\times 100=10\,000$
$(8.5)^{2}=(8.5)\times(8.5)=72.25$
$(1.35)^{2}=(1.35)\times(1.35)=1.8225$
2) Calculons les cubes des nombres suivants.
$3^{3}=3\times 3\times 3=27$
$100^{3}=100\times 100\times 100=1\,000\,000$
$(7.1)^{3}=(7.1)\times(7.1)\times(7.1)=357.911$
$(6.3)^{3}=(6.3)\times(6.3)\times(6.3)=250.047$
$200^{3}=200\times 200\times 200=8\,000\,000$
Exercice 8
Après avoir transformé sous la forme d'un produit de facteur, calculons.
a)
$2^{2}=2\times 2=4$
$19^{2}=19\times 19=361$
$(1.2)^{2}=(1.2)\times(1.2)=1.44$
$(15.5)^{2}=(15.5)\times(15.5)=240.25$
b)
$2^{3}=2\times 2\times 2=8$
$19^{2}=19\times 19\times 19=6\,859$
$(1.2)^{2}=(1.2)\times(1.2)\times(1.2)=1.728$
$(15.5)^{2}=(15.5)\times(15.5)\times(15.5)=3\,723.875$
Exercice 9
1) $16\;;\ 25\;;\ 100\ $ et $\ 2.25$ sont des carrés.
En effet, on a :
$4^{2}=16$
$5^{2}=25$
$10^{2}=100$
$(1.5)^{2}=2.25$
2) $8\;;\ 27\;;\ 216\ $ et $\ 1\,000$ sont des cubes.
En effet, on a :
$2^{3}=8$
$3^{3}=27$
$6^{3}=216$
$10^{3}=1\,000$
Exercice 10
Mettons sous la forme de puissances simples.
a) $2\times 2\times 2=2^{3}$
b) $4\times 4=4^{2}$
c) $3.5\times 3.5\times 3.5=(3.5)^{3}$
d) $18.7\times 18.7=(18.7)^{2}$
Exercice 11
Reproduisons et complétons le tableau suivant :
$$\begin{array}{|c|c|c|c|c|c|c|}\hline a&b&c&a\times b&(a\times b)\times c&b\times c&a\times(b\times c)\\\hline 42&0.9&1.3&37.8&49.14&1.17&49.14\\\hline 72&9.7&1.6&698.4&1\,117.44&15.52&1\,117.44\\\hline 324.7&5.2&1.9&1\,688.44&3\,208.036&9.88&3\,208.036\\\hline \end{array}$$
Exercice 12
1) Reproduisons et complétons le tableau suivant :
$$\begin{array}{|c|c|c|}\hline a&a\times 1&1\times a\\\hline 0.9&0.9&0.9\\\hline 9.7&9.7&9.7\\\hline 5.235&5.235&5.235\\\hline \end{array}$$
2) Comparons pour chacune des valeurs de $a\;,\ a\times 1\ $ et $\ 1\times a$
En observant les résultats du tableau ci-dessus, on peut dire :
Pour $a=0.9$, on a : $0.9\times 1=0.9\ $ et $\ 1\times 0.9=0.9$
Donc, $0.9\times 1=1\times 0.9=0.9$
Pour $a=9.7$, on a : $9.7\times 1=9.7\ $ et $\ 1\times 9.7=9.7$
Ainsi, $9.7\times 1=1\times 9.7=9.7$
Pour $a=5.235$, on a : $5.235\times 1=5.235\ $ et $\ 1\times 5.23=5.235$
D'où, $5.235\times 1=1\times 5.235=5.235$
Exercice 13
1) Reproduisons et complète le tableau suivant :
$$\begin{array}{|c|c|c|}\hline a&a\times 0&0\times a\\\hline 42&0&0\\\hline 72.3&0&0\\\hline 324.765&0&0\\\hline \end{array}$$
2) Comparons pour chacune des valeurs de $a\;,\ a\times 0\ $ et $\ 0\times a$
En observant les résultats du tableau ci-dessus, on peut dire :
Pour $a=42$, on a : $42\times 0=0\ $ et $\ 0\times 42=0$
Donc, $42\times 0=0\times 42=0$
Pour $a=72.3$, on a : $72.3\times 0=0\ $ et $\ 0\times 72.3=0$
Ainsi, $72.3\times 0=0\times 72.3=0$
Pour $a=324.765$, on a : $324.765\times 0=0\ $ et $\ 0\times 324.765=0$
D'où, $324.765\times 0=0\times 324.765=0$
Exercice 14
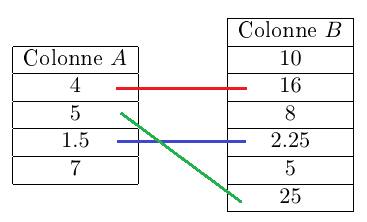
1) Recopions les tableaux ci-dessous et relions chaque nombre de la colonne $A$ à son carré dans la colonne $B\ :$
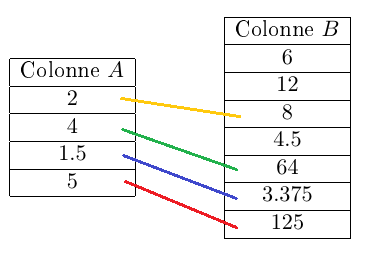
2) Recopions les tableaux ci-dessous et relions chaque nombre de la colonne $A$ à son cube dans la colonne $B\ :$
Exercice 15
Un camion livre $18$ palettes à un supermarché. Sur chaque palette ; il y a $18$ cartons, et dans chaque carton il y a $18$ boites de conserve.
Calculons le nombre de boites de conserve qu'il y a en tout.
On sait que sur chaque palette ; il y a $18$ cartons. Or, on a $18$ palettes.
Donc, le nombre de cartons est :
$$\text{nombre de cartons}=18\times\text{nombre de palettes}=18\times 18$$
Comme dans chaque carton il y a $18$ boites de conserve alors, le nombre de boites de conserve qu'il y a en tout est égal à :
$\begin{array}{rcl} \text{nombre de boites de conserve}&=&18\times\text{nombre de cartons}\\\\&=&18\times(18\times 18)\\\\&=&18\times 18\times 18\\\\&=&18^{3}\\\\&=&5\,832\end{array}$
D'où, il y a en tout $5\,832$ boites de conserve.
Exercice 16
Un commerçant achète $7$ rouleaux de $50\;m$ de tissu. Il paie chaque rouleau $22\,500\;F.$ Il revend le tissu au prix de $835$ francs le mètre.
Calculons le bénéfice réalisé par ce commerçant lorsqu'il aura revendu la totalité du tissu.
On a :
$$\text{bénéfice}=\text{prix de vente}-\text{prix d'achat}$$
Comme, il y a $7$ rouleaux et chaque rouleau coûte $22\,500\;F$ alors, on a :
$$\text{prix d'achat}=7\times 22\,500\;F$$
De plus, comme il revend le tissu au prix de $835$ francs le mètre alors, on a :
$$\text{prix de vente}=\text{longueur du tissu}\times 835\;F$$
Or, il y a $7$ rouleaux de tissu et chaque rouleau mesure $50\;m$ donc, la longueur de tissu acheté est :
$$\text{longueur de tissu acheté}=7\times 50\;m$$
Ainsi, le prix de vente est donné par :
$$\text{prix de vente}=(7\times 50)\times 835\;F$$
Alors, en remplaçant le prix d'achat et le prix de vente dans l'écriture du bénéfice, on trouve :
$\begin{array}{rcl}\text{bénéfice}&=&\text{prix de vente}-\text{prix d'achat}\\\\&=&(7\times 50)\times 835-7\times 22\,500\\\\&=&350\times 835-7\times 22\,500\\\\&=&292\,250-157\,500\\\\&=&134\,750\end{array}$
Donc, le bénéfice réalisé par ce commerçant est égal à $134\,750\;F.$
Exercice 17
Robert dispose de $10\,000\;F$ et veut acheter $12$ cahiers à $250\;F$ l'un, $8$ stylos à $100\;F$ l'un et $5$ livres coûtant chacun $950\;F.$
On a :
$$\text{prix des fournitures}=\text{prix des cahiers}+\text{prix des stylos}+\text{prix des livres}$$
Avec :
$\text{prix des cahiers}=12\times 250\;F$
$\text{prix des stylos}=8\times 100\;F$
$\text{prix des livres}=5\times 950\;F$
Donc, en remplaçant, on obtient :
$\begin{array}{rcl}\text{prix des fournitures}&=&\text{prix des cahiers}+\text{prix des stylos}+\text{prix des livres}\\\\&=&12\times 250+8\times 100+5\times 950\\\\&=&3\,000+800+4\,750\end{array}$
Ainsi, on a :
$$\text{prix des fournitures}=3\,000\;F+800\;F+4\,750\;F$$
En arrondissant l'ordre de grandeur de chaque terme au millier le plus proche, on obtient :
$3\,000$ est plus proche de $3\,000$
$800$ est plus proche de $1\,000$
$4\,750$ est plus proche de $5\,000$
Alors, une estimation du prix des fournitures est donnée par :
$$3\,000\;F+1\,000\;F+5\,000\;F=9\,000\;F$$
Comme Robert dispose de $10\,000\;F$ alors, il a assez d'argent pour payer sa fourniture.
Auteur:
Diny Faye

Commentaires
Papa (non vérifié)
jeu, 03/11/2021 - 23:37
Permalien
Maitre
mahamadou (non vérifié)
jeu, 06/10/2021 - 14:33
Permalien
Merci votre exo mais je vous
Amady (non vérifié)
ven, 03/07/2025 - 21:53
Permalien
Lycée ndiob
Amady (non vérifié)
ven, 03/07/2025 - 21:56
Permalien
Les devoires
Ajouter un commentaire