Solution des exercices : Équation du premier degré à une inconnue - 4e
Classe:
Quatrième
Exercice 1 Vocabulaire
Recopions puis complétons parles mots qui conviennent.
1) Une équation du premier degré à une inconnue est une équation dans laquelle un nombre est inconnu.
2) Résoudre l'équation, c'est trouver toutes les valeurs de l'inconnue pour lesquelles l'équation est vérifiée.
3) Les valeurs de l'inconnue sont les nombres qui vérifient l'équation.
4) On ne change pas les signes d'une équation lorsqu'on ajoute le même nombre dans chaque membre.
5) Dans l'équation : $2x-4=7\;;\quad 2x-4$ est le membre de gauche et $7$ est le membre de droite.
Exercice 2 "Équation de la forme $x+a=b$"
Résolvons dans $\mathbb{Q}$ chacune des équations suivantes en utilisant les propriétés des inégalités.
Résoudre une équation du type $x+a=b$ revient à trouver les valeurs de $x$ tels que :
$$x=b-a$$
Donc, il faut juste changer $a$ de membre ; de la gauche vers la droite sans oublier de changer son signe.
a) Soit à résoudre l'équation : $x+3=6$
Pour trouver la solution, on va changer $+3$ de membre (de la gauche vers la droite) pour devenir $-3.$
Donc, on obtient : $x=6-3$
Ce qui donne : $x=3$
Comme $3\in\mathbb{Q}\ $ alors, $\boxed{S=\{3\}}$
b) Soit l'équation : $x+5=-6$
Pour résoudre cette équation, on fait passer $+5$ de la gauche vers la droite en changeant son signe.
Ce qui entraîne : $x=-6-5=-11$
Or, $-11\in\mathbb{Q}\ $ donc, $\boxed{S=\{-11\}}$
c) Soit l'équation : $x+3=-8$
On procède comme dans les questions a) et b).
On a : $x+3=-8$ si, et seulement si, $x=-8-3=-11$
Comme $-11\in\mathbb{Q}\ $ alors, $\boxed{S=\{-11\}}$
d) Soit l'équation : $x-4=2$
On a : $x-4=2$ si, et seulement si, $x=2+4=6$
$6\in\mathbb{Q}\ $ donc, $\boxed{S=\{6\}}$
e) Soit à résoudre l'équation : $x-1=-4$
On a :
$\begin{array}{rcl} x-1=-4&\Leftrightarrow&x=-4+1\\\\&\Leftrightarrow&x=-3\end{array}$
Comme $-3\in\mathbb{Q}$ alors, $\boxed{S=\{-3\}}$
f) Soit à résoudre l'équation : $-4+x=-4$
L'équation $-4+x=-4$ peut aussi s'écrire $x-4=-4$
Donc, on applique la même méthode en changeant de membre le nombre $-4$ de la gauche vers la droite.
Ainsi, on obtient :
$\begin{array}{rcl} -4+x=-4&\Leftrightarrow&x=-4+4\\\\&\Leftrightarrow&x=0\end{array}$
Comme $0$ est un élément de $\mathbb{Q}$ alors, l'ensemble des solutions de l'équation est donnée par : $\boxed{S=\{0\}}$
g) Soit à résoudre l'équation : $x-\dfrac{2}{5}=\dfrac{4}{3}$
On a :
$\begin{array}{rcl} x-\dfrac{2}{5}=\dfrac{4}{3}&\Leftrightarrow&x=\dfrac{4}{3}+\dfrac{2}{5}\\ \\&\Leftrightarrow&x=\dfrac{20}{15}+\dfrac{6}{15}\\ \\&\Leftrightarrow&x=\dfrac{26}{15}\end{array}$
Comme $\dfrac{26}{15}\in\mathbb{Q}\ $ alors, $\boxed{S=\left\{\dfrac{26}{15}\right\}}$
h) Soit à résoudre l'équation : $x+\dfrac{1}{3}=\dfrac{3}{2}$
On a :
$\begin{array}{rcl} x+\dfrac{1}{3}=\dfrac{3}{2}&\Leftrightarrow&x=\dfrac{3}{2}-\dfrac{1}{3}\\ \\&\Leftrightarrow&x=\dfrac{9}{6}-\dfrac{2}{6}\\ \\&\Leftrightarrow&x=\dfrac{7}{6}\end{array}$
Or, $\dfrac{7}{6}\in\mathbb{Q}\ $ donc, $\boxed{S=\left\{\dfrac{7}{6}\right\}}$
i) Soit à résoudre l'équation : $x-\dfrac{4}{5}=-\dfrac{1}{3}$
On a :
$\begin{array}{rcl} x-\dfrac{4}{5}=-\dfrac{1}{3}&\Leftrightarrow&x=-\dfrac{1}{3}+\dfrac{4}{5}\\ \\&\Leftrightarrow&x=-\dfrac{5}{15}+\dfrac{12}{15}\\ \\&\Leftrightarrow&x=\dfrac{7}{15}\end{array}$
Or, $\dfrac{7}{15}\in\mathbb{Q}\ $ donc, $\boxed{S=\left\{\dfrac{7}{15}\right\}}$
j) Soit à résoudre l'équation : $-\dfrac{2}{5}+x=\dfrac{1}{2}$
$\begin{array}{rcl} -\dfrac{2}{5}+x=\dfrac{1}{2}&\Leftrightarrow&x=\dfrac{1}{2}+\dfrac{2}{5}\\ \\&\Leftrightarrow&x=\dfrac{5}{10}+\dfrac{4}{10}\\ \\&\Leftrightarrow&x=\dfrac{9}{10}\end{array}$
Comme, $\dfrac{9}{10}\in\mathbb{Q}\ $ alors, $\boxed{S=\left\{\dfrac{9}{10}\right\}}$
l) Soit à résoudre l'équation : $x-\dfrac{4}{5}=\dfrac{1}{3}$
On a :
$\begin{array}{rcl} x-\dfrac{4}{5}=\dfrac{1}{3}&\Leftrightarrow&x=\dfrac{1}{3}+\dfrac{4}{5}\\ \\&\Leftrightarrow&x=\dfrac{5}{15}+\dfrac{12}{15}\\ \\&\Leftrightarrow&x=\dfrac{17}{15}\end{array}$
Comme, $\dfrac{17}{15}\in\mathbb{Q}\ $ alors, $\boxed{S=\left\{\dfrac{17}{15}\right\}}$
m) Soit à résoudre l'équation : $-x+\dfrac{1}{5}=-\dfrac{1}{3}$
On a :
$\begin{array}{rcl} -x+\dfrac{1}{5}=-\dfrac{1}{3}&\Leftrightarrow&-x=-\dfrac{1}{3}-\dfrac{1}{5}\\ \\&\Leftrightarrow&-x=-\dfrac{5}{15}-\dfrac{3}{15}\\ \\&\Leftrightarrow&-x=-\dfrac{8}{15}\end{array}$
Par suite, en multipliant chaque membre de l'équation $-x=-\dfrac{8}{15}$ par $-1$, on obtient :
$(-1)\times(-x)=(-1)\times\left(-\dfrac{8}{15}\right)\ \Leftrightarrow\ x=\dfrac{8}{15}$
Or, $\dfrac{8}{15}\in\mathbb{Q}\ $ donc, $\boxed{S=\left\{\dfrac{8}{15}\right\}}$
Exercice 3 "Équation de la forme $ax=b$"
Résolvons dans $\mathbb{Q}$ chacune des équations suivantes en utilisant les propriétés des inégalités.
Résoudre dans $\mathbb{Q}$ une équation de la forme $ax=b\;;\ (a\neq 0)$ revient à déterminer les valeurs de $x$ telles que :
$$x=\dfrac{b}{a}$$
Si $\dfrac{b}{a}\in\mathbb{Q}$ alors, l'ensemble des solutions $(S)$ sera donnée par :
$$S=\left\{\dfrac{b}{a}\right\}$$
a) Soit à résoudre l'équation suivante : $4x=3$
On a : $4x=3\ \Leftrightarrow\ x=\dfrac{3}{4}$
Comme $\dfrac{3}{4}\in\mathbb{Q}\ $ alors, $\boxed{S=\left\{\dfrac{3}{4}\right\}}$
b) Soit à résoudre l'équation suivante : $-2x=4.8$
Alors : $-2x=4.8\ \Leftrightarrow\ x=\dfrac{4.8}{-2}=-2.4$
Or, $-2.4\in\mathbb{Q}$
Par suite ; $\boxed{S=\{-2.4\}}$
c) Soit à résoudre l'équation suivante : $3x=-19$
On a : $3x=-19\ \Leftrightarrow\ x=\dfrac{-19}{3}$
Or, $\dfrac{-19}{3}\in\mathbb{Q}\ $ donc, $\boxed{S=\left\{\dfrac{-19}{3}\right\}}$
d) Soit à résoudre l'équation suivante : $2x=\dfrac{3}{7}$
Alors :
$\begin{array}{rcl} 2x=\dfrac{3}{7}&\Leftrightarrow&x=\dfrac{\dfrac{3}{7}}{2}\\ \\&\Leftrightarrow&x=\dfrac{3}{7}\times\dfrac{1}{2}\\ \\&\Leftrightarrow&x=\dfrac{3}{14}\end{array}$
$\dfrac{3}{14}$ étant un élément de $\mathbb{Q}$ donc, $\boxed{S=\left\lbrace\dfrac{3}{14}\right\rbrace}$
e) Soit à résoudre l'équation suivante : $-2x=-\dfrac{7}{3}$
Alors :
$\begin{array}{rcl} -2x=-\dfrac{7}{3}&\Leftrightarrow&x=\dfrac{-\dfrac{7}{3}}{-2}\\ \\&\Leftrightarrow&x=\left(-\dfrac{7}{3}\right)\times\left(-\dfrac{1}{2}\right)\\ \\&\Leftrightarrow&x=\dfrac{7}{3}\times\dfrac{1}{2}\\ \\&\Leftrightarrow&x=\dfrac{7}{6}\end{array}$
Or, $\dfrac{7}{6}\in\mathbb{Q}\ $ donc, $\boxed{S=\left\lbrace\dfrac{7}{6}\right\rbrace}$
f) Soit à résoudre l'équation suivante : $\dfrac{4}{3}x=-\dfrac{9}{8}$
On a :
$\begin{array}{rcl}\dfrac{4}{3}x=-\dfrac{9}{8}&\Leftrightarrow&x=\dfrac{-\dfrac{9}{8}}{\dfrac{4}{3}}\\ \\&\Leftrightarrow&x=-\dfrac{9}{8}\times\dfrac{3}{4}\\ \\&\Leftrightarrow&x=-\dfrac{27}{32}\end{array}$
Comme, $-\dfrac{27}{32}\in\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace -\dfrac{27}{32}\right\rbrace}$
Exercice 4 "Équation de la forme $ax+b=c$"
Résolvons dans $\mathbb{Q}$ chacune des équations suivantes.
Résoudre dans $\mathbb{Q}$ une équation de la forme $ax+b=c$ revient à déterminer les valeurs de $x$ telles que :
$$x=\dfrac{c-b}{a}$$
Si $\dfrac{c-b}{a}\in\mathbb{Q}$ alors, l'ensemble des solutions $(S)$ sera donnée par :
$$S=\left\{\dfrac{c-b}{a}\right\}$$
a) Soit à résoudre l'équation suivante : $-2x-1=5$
On a :
$\begin{array}{rcl} -2x-1=5&\Leftrightarrow&-2x=5+1\\ \\&\Leftrightarrow&-2x=6\\ \\&\Leftrightarrow&x=\dfrac{6}{-2}\\\\&\Leftrightarrow&x=-3\end{array}$
Or, on sait que $-3\in\mathbb{Q}\ $ donc, $\boxed{S=\left\lbrace -3\right\rbrace}$
b) Soit à résoudre l'équation suivante : $-4x+2=5$
Alors on a :
$\begin{array}{rcl} -4x+2=5&\Leftrightarrow&-4x=5-2\\ \\&\Leftrightarrow&-4x=3\\ \\&\Leftrightarrow&x=\dfrac{3}{-4}\\\\&\Leftrightarrow&x=-\dfrac{3}{4}\end{array}$
Comme $-\dfrac{3}{4}\in\mathbb{Q}\ $ donc, $\boxed{S=\left\lbrace -\dfrac{3}{4}\right\rbrace}$
c) Soit à résoudre l'équation suivante :$-6x-1=-7$
On a :
$\begin{array}{rcl} -6x-1=-7&\Leftrightarrow&-6x=-7+1\\ \\&\Leftrightarrow&-6x=-6\\ \\&\Leftrightarrow&x=\dfrac{-6}{-6}\\\\&\Leftrightarrow&x=1\end{array}$
Comme, $1\in\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace 1\right\rbrace}$
d) Soit à résoudre l'équation suivante : $-\dfrac{3}{4}x-1=2$
On a :
$\begin{array}{rcl} -\dfrac{3}{4}x-1=2&\Leftrightarrow&-\dfrac{3}{4}x=2+1\\ \\&\Leftrightarrow&-\dfrac{3}{4}x=3\\ \\&\Leftrightarrow&x=\dfrac{3}{-\dfrac{3}{4}}\\\\&\Leftrightarrow&x=3\times\left(-\dfrac{4}{3}\right)\\\\&\Leftrightarrow&x=\dfrac{3\times(-4)}{3}\\\\&\Leftrightarrow&x=-4\end{array}$
Or, $-4\in\mathbb{Q}\ $ donc, $\boxed{S=\left\lbrace -4\right\rbrace}$
e) Soit à résoudre l'équation suivante : $\dfrac{6}{5}x-\dfrac{1}{3}=3$
On a :
$\begin{array}{rcl} \dfrac{6}{5}x-\dfrac{1}{3}=3&\Leftrightarrow&\dfrac{6}{5}x=3+\dfrac{1}{3}\\ \\&\Leftrightarrow&\dfrac{6}{5}x=\dfrac{9}{3}+\dfrac{1}{3}\\ \\&\Leftrightarrow&\dfrac{6}{5}x=\dfrac{10}{3}\\\\&\Leftrightarrow&x=\dfrac{\dfrac{10}{3}}{\dfrac{6}{5}}\\\\&\Leftrightarrow&x=\dfrac{10}{3}\times\dfrac{5}{6}\\\\&\Leftrightarrow&x=\dfrac{10\times 5}{3\times 6}\\\\&\Leftrightarrow&x=\dfrac{50}{18}\end{array}$
Comme $\dfrac{50}{18}\in\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace \dfrac{50}{18}\right\rbrace}$
f) Soit à résoudre l'équation suivante : $-2x+\dfrac{1}{4}=\dfrac{1}{3}$
On a :
$\begin{array}{rcl} -2x+\dfrac{1}{4}=\dfrac{1}{3}&\Leftrightarrow&-2x=\dfrac{1}{3}-\dfrac{1}{4}\\ \\&\Leftrightarrow&-2x=\dfrac{4}{12}-\dfrac{3}{12}\\\\&\Leftrightarrow&-2x=\dfrac{4-3}{12}\\\\&\Leftrightarrow&-2x=\dfrac{1}{12}\\\\&\Leftrightarrow&x=\dfrac{\dfrac{1}{12}}{-2}\\\\&\Leftrightarrow&x=\dfrac{1}{12}\times\dfrac{1}{-2}\\\\&\Leftrightarrow&x=\dfrac{1\times 1}{12\times(-2)}\\\\&\Leftrightarrow&x=\dfrac{1}{-24}\\\\&\Leftrightarrow&x=-\dfrac{1}{24}\end{array}$
Comme $-\dfrac{1}{24}\in\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace -\dfrac{1}{24}\right\rbrace}$
Exercice 5 "Équation de la forme $ax+b=cx+d$"
Pour résoudre dans $\mathbb{Q}$ une équation de la forme $ax+b=cx+d$, on regroupe les termes en $x$ dans un membre et les autres termes dans l'autre membre.
De plus, chaque terme qui change de membre change de signe.
Résolvons dans $\mathbb{Q}$ chacune des équations suivantes.
a) Soit à résoudre l'équation suivante : $2x+3=4x+5$
En regroupant les termes en $x$ dans le membre de gauche et les autres termes dans le membre de droite, on obtient :
$\begin{array}{rcl} 2x+3=4x+5&\Leftrightarrow&2x-4x=5-3\\ \\&\Leftrightarrow&-2x=2\\\\&\Leftrightarrow&x=\dfrac{2}{-2}\\\\&\Leftrightarrow&x=-1\end{array}$
$-1$ étant un élément de $\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace -1\right\rbrace}$
b) Soit à résoudre l'équation suivante : $2x-3=-4x+5$
On a :
$\begin{array}{rcl} 2x-3=-4x+5&\Leftrightarrow&2x+4x=5+3\\ \\&\Leftrightarrow&6x=8\\\\&\Leftrightarrow&x=\dfrac{8}{6}\end{array}$
Comme $\dfrac{8}{6}$ appartient à $\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace \dfrac{8}{6}\right\rbrace}$
c) Soit à résoudre l'équation suivante : $-2x+3.5=4x-5$
Alors, on a :
$\begin{array}{rcl} -2x+3.5=4x-5&\Leftrightarrow&-2x-4x=-5-3.5\\ \\&\Leftrightarrow&-6x=-8.5\\\\&\Leftrightarrow&x=\dfrac{-8.5}{-6}\\\\&\Leftrightarrow&x=\dfrac{8.5}{6}\end{array}$
Or, on sait que : $\dfrac{8.5}{6}=\dfrac{8.5\times 10}{6\times 10}=\dfrac{85}{60}$
De plus, $\dfrac{85}{60}\in\mathbb{Q}\ $ donc, $\boxed{S=\left\lbrace \dfrac{85}{60}\right\rbrace}$
d) Soit à résoudre l'équation suivante : $-2x-3=-4x+5$
On a :
$\begin{array}{rcl} -2x-3=-4x+5&\Leftrightarrow&-2x+4x=5+3\\ \\&\Leftrightarrow&2x=8\\\\&\Leftrightarrow&x=\dfrac{8}{2}\\\\&\Leftrightarrow&x=4\end{array}$
Comme, $4\in\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace 4\right\rbrace}$
e) Soit à résoudre l'équation suivante : $3-4x+3=5-6x$
Alors, on a :
$\begin{array}{rcl} 3-4x+3=5-6x&\Leftrightarrow&-4x+6x=5-3-3\\ \\&\Leftrightarrow&2x=-1\\\\&\Leftrightarrow&x=\dfrac{-1}{2}\end{array}$
Comme, $\dfrac{-1}{2}\in\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace \dfrac{-1}{2}\right\rbrace}$
f) Soit à résoudre l'équation suivante : $-3-4x=-1.5-7x$
Alors, on a :
$\begin{array}{rcl} -3-4x=-1.5-7x&\Leftrightarrow&-4x+7x=-1.5+3\\ \\&\Leftrightarrow&3x=1.5\\\\&\Leftrightarrow&x=\dfrac{1.5}{3}\\\\&\Leftrightarrow&x=0.5\end{array}$
Or, $0.5$ est un élément de $\mathbb{Q}\ $ donc, $\boxed{S=\left\lbrace 0.5\right\rbrace}$
g) Soit à résoudre l'équation suivante : $3x-4=8.3$Alors, on a :
$\begin{array}{rcl} 3x-4=8.3&\Leftrightarrow&3x=8.3+4\\ \\&\Leftrightarrow&3x=12.3\\\\&\Leftrightarrow&x=\dfrac{12.3}{3}\\\\&\Leftrightarrow&x=4.1\end{array}$
Comme $4.1$ est un élément de $\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace 4.1\right\rbrace}$
h) Soit à résoudre l'équation suivante : $-5x+7=6$
On a :
$\begin{array}{rcl} -5x+7=6&\Leftrightarrow&-5x=6-7\\ \\&\Leftrightarrow&-5x=-1\\\\&\Leftrightarrow&x=\dfrac{-1}{-5}\\\\&\Leftrightarrow&x=\dfrac{1}{5}\end{array}$
Comme $\dfrac{1}{5}\in\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace \dfrac{1}{5}\right\rbrace}$
i) Soit à résoudre l'équation suivante : $2x-2=2x$
Alors, on a :
$\begin{array}{rcl} 2x-2=2x&\Leftrightarrow&2x-2x=2\\ \\&\Leftrightarrow&0x=2\end{array}$
On sait qu'il n'existe aucun nombre rationnel $x$ vérifiant : $0\times x=2$
Par conséquent, $\boxed{S=\emptyset}$
Exercice 6
Résolvons dans $\mathbb{Q}$ chacune des équations suivantes.
a) $4(1-3x)=-3(2-x)$
On commence par développer et ensuite on applique les mêmes règles que dans les exercices précédents.
Ainsi, on a :
$\begin{array}{rcl} 4(1-3x)=-3(2-x)&\Leftrightarrow&4\times 1-4\times(3x)=-3\times 2-3\times(-x)\\ \\&\Leftrightarrow&4-12x=-6+3x\\\\&\Leftrightarrow&-12x-3x=-6-4\\\\&\Leftrightarrow&-15x=-10\\\\&\Leftrightarrow&x=\dfrac{-10}{-15}\\\\&\Leftrightarrow&x=\dfrac{10}{15}\end{array}$
Comme $\dfrac{10}{15}\in\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace \dfrac{10}{15}\right\rbrace}$
b) $(3x-1)-(x-1)=3x-5$
En développant puis en appliquant les mêmes règles que dans les exercices précédents, on obtient :
$\begin{array}{rcl} (3x-1)-(x-1)=3x-5&\Leftrightarrow&3x-1-x+1=3x-5\\ \\&\Leftrightarrow&3x-x-3x=-5+1-1\\\\&\Leftrightarrow&-x=-5\\\\&\Leftrightarrow&x=\dfrac{-5}{-1}\\\\&\Leftrightarrow&x=5\end{array}$
$5$ étant un élément de $\mathbb{Q}\ $ donc, $\boxed{S=\left\lbrace 5\right\rbrace}$
c) $6(2x-1)-2(-2x+3)=0$
En développant puis en appliquant les mêmes règles que dans les exercices précédents, on obtient :
$\begin{array}{rcl} 6(2x-1)-2(-2x+3)=0&\Leftrightarrow&6\times 2x-6\times 1-2\times(-2x)-2\times 3=0\\ \\&\Leftrightarrow&12x-6+4x-6=0\\\\&\Leftrightarrow&16x-12=0\\\\&\Leftrightarrow&16x=12\\\\&\Leftrightarrow&x=\dfrac{12}{16}\end{array}$
Or, $\dfrac{12}{16}$ est un élément de $\mathbb{Q}\ $ donc, $\boxed{S=\left\lbrace \dfrac{12}{16}\right\rbrace}$
d) $2(x-1)-3(-4x+7)=0$
On commence par développer puis on applique les mêmes règles que dans les exercices précédents.
$\begin{array}{rcl} 2(x-1)-3(-4x+7)=0&\Leftrightarrow&2\times x-2\times 1-3\times(-4x)-3\times 7=0\\ \\&\Leftrightarrow&2x-2+12x-21=0\\\\&\Leftrightarrow&14x-23=0\\\\&\Leftrightarrow&14x=23\\\\&\Leftrightarrow&x=\dfrac{23}{14}\end{array}$
Comme $\dfrac{23}{14}$ est un élément de $\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace \dfrac{23}{14}\right\rbrace}$
e) $-2(1-3x)=-3(2-x)$
On commence par développer puis on applique les mêmes règles que dans les exercices précédents.
$\begin{array}{rcl} -2(1-3x)=-3(2-x)&\Leftrightarrow&-2\times 1-2\times(-3x)=-3\times 2-3\times(-x)\\ \\&\Leftrightarrow&-2+6x=-6+3x\\\\&\Leftrightarrow&6x-3x=-6+2\\\\&\Leftrightarrow&3x=-4\\\\&\Leftrightarrow&x=\dfrac{-4}{3}\end{array}$
Comme $\dfrac{-4}{3}$ est un élément de $\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace \dfrac{-4}{3}\right\rbrace}$
f) $-3(1-3x)=2(2-x)+5$
En développant puis en appliquant les mêmes règles que dans les exercices précédents, on obtient :
$\begin{array}{rcl} -3(1-3x)=2(2-x)+5&\Leftrightarrow&-3\times 1-3\times(-3x)=2\times 2+2\times(-x)+5\\ \\&\Leftrightarrow&-3+9x=4-2x+5\\\\&\Leftrightarrow&9x+2x=4+5+3\\\\&\Leftrightarrow&11x=12\\\\&\Leftrightarrow&x=\dfrac{12}{11}\end{array}$
Or, $\dfrac{12}{11}$ est un élément de $\mathbb{Q}\ $ donc, $\boxed{S=\left\lbrace \dfrac{12}{11}\right\rbrace}$
g) $3x-6(3-4x)=9x-2$
En développant puis en appliquant les mêmes règles que dans les exercices précédents, on obtient :
$\begin{array}{rcl} 3x-6(3-4x)=9x-2&\Leftrightarrow&3x-6\times 3-6\times(-4x)=9x-2\\ \\&\Leftrightarrow&3x-18+24x=9x-2\\\\&\Leftrightarrow&3x+24x-9x=-2+18\\\\&\Leftrightarrow&18x=16\\\\&\Leftrightarrow&x=\dfrac{16}{18}\end{array}$
Comme $\dfrac{16}{18}$ est un élément de $\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace \dfrac{16}{18}\right\rbrace}$
h) Soit à résoudre l'équation suivante : $3x-2(x^{2}-1)=-2x^{2}-2$
Alors, on a :
$\begin{array}{rcl} 3x-2(x^{2}-1)=-2x^{2}-2&\Leftrightarrow&3x-2\times(x^{2})-2\times(-1)=-2x^{2}-2\\ \\&\Leftrightarrow&3x-2x^{2}+2=-2x^{2}-2\\\\&\Leftrightarrow&3x-2x^{2}+2x^{2}=-2-2\\\\&\Leftrightarrow&3x=-4\\\\&\Leftrightarrow&x=\dfrac{-4}{3}\end{array}$
Comme $\dfrac{-4}{3}$ est un élément de $\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace \dfrac{-4}{3}\right\rbrace}$
3) Résolvons dans $\mathbb{Q}$ chacune des équations suivantes.
a) Soit à résoudre l'équation suivante : $-\dfrac{8}{7}x+2=1$
Alors, on a :
$\begin{array}{rcl} -\dfrac{8}{7}x+2=1&\Leftrightarrow&-\dfrac{8}{7}x=1-2\\ \\&\Leftrightarrow&-\dfrac{8}{7}x=-1\\\\&\Leftrightarrow&x=\dfrac{-1}{-\dfrac{8}{7}}\\\\&\Leftrightarrow&x=(-1)\times\left(-\dfrac{7}{8}\right)\\\\&\Leftrightarrow&x=\dfrac{7}{8}\end{array}$
Comme $\dfrac{7}{8}$ est un élément de $\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace \dfrac{7}{8}\right\rbrace}$
b) Soit à résoudre l'équation suivante : $\dfrac{8}{7}x-8=1-x$
On a :
$\begin{array}{rcl} \dfrac{8}{7}x-8=1-x&\Leftrightarrow&\dfrac{8}{7}x+x=1+8\\ \\&\Leftrightarrow&\dfrac{8}{7}x+\dfrac{7}{7}x=9\\\\&\Leftrightarrow&\dfrac{15}{7}x=9\\\\&\Leftrightarrow&x=\dfrac{9}{\dfrac{15}{7}}\\\\&\Leftrightarrow&x=9\times\dfrac{7}{15}\\\\&\Leftrightarrow&x=\dfrac{63}{15}\end{array}$
$\dfrac{63}{15}$ étant un élément de $\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace \dfrac{63}{15}\right\rbrace}$
c) Soit à résoudre l'équation suivante : $\dfrac{3}{4}x-2x=-3+x$
Alors, on a :
$\begin{array}{rcl} \dfrac{3}{4}x-2x=-3+x&\Leftrightarrow&\dfrac{3}{4}x-2x-x=-3\\ \\&\Leftrightarrow&\dfrac{3}{4}x-\dfrac{8}{4}x-\dfrac{1}{4}x=-3\\\\&\Leftrightarrow&-\dfrac{6}{4}x=-3\\\\&\Leftrightarrow&x=\dfrac{-3}{-\dfrac{6}{4}}\\\\&\Leftrightarrow&x=(-3)\times\left(-\dfrac{4}{6}\right)\\\\&\Leftrightarrow&x=\dfrac{12}{6}\\\\&\Leftrightarrow&x=2\end{array}$
Comme $2\in\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace 2\right\rbrace}$
d) Soit à résoudre l'équation suivante : $\dfrac{2}{3}(5x-1)=\dfrac{3}{4}(x-3)$
En développant puis en regroupant les termes en $x$ dans le membre de gauche et les autres termes dans le membre de droite, on obtient :
$\begin{array}{rcl} \dfrac{2}{3}(5x-1)=\dfrac{3}{4}(x-3)&\Leftrightarrow&\dfrac{2}{3}\times(5x)-\dfrac{2}{3}\times 1=\dfrac{3}{4}\times x-\dfrac{3}{4}\times 3\\ \\&\Leftrightarrow&\dfrac{10}{3}x-\dfrac{2}{3}=\dfrac{3}{4}x-\dfrac{9}{4}\\\\&\Leftrightarrow&\dfrac{10}{3}x-\dfrac{3}{4}x=-\dfrac{9}{4}+\dfrac{2}{3}\\\\&\Leftrightarrow&\dfrac{40}{12}x-\dfrac{9}{12}x=-\dfrac{27}{12}+\dfrac{8}{12}\\\\&\Leftrightarrow&\dfrac{31}{12}x=-\dfrac{19}{12}\\\\&\Leftrightarrow&x=\dfrac{-\dfrac{19}{12}}{\dfrac{31}{12}}\\\\&\Leftrightarrow&x=-\dfrac{19}{12}\times\dfrac{12}{31}\\\\&\Leftrightarrow&x=-\dfrac{19}{31}\end{array}$
Comme $-\dfrac{19}{31}\in\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace -\dfrac{19}{31}\right\rbrace}$
Exercice 7 "Équation produit"
1) Résolvons dans $\mathbb{Q}$ chacune des équations suivantes.
Rappel : un produit de facteurs est nul si au moins l'un des facteurs est nul. Ainsi :
$$(ax+b)(cx+d)=0\ \Leftrightarrow\ ax+b=0\ \text{ ou }\ cx+d=0$$
a) Soit à résoudre l'équation suivante : $(x-4)(x+5)=0$
Alors, on a :
$\begin{array}{rcl} (x-4)(x+5)=0&\Leftrightarrow&x-4=0\ \text{ ou }\ x+5=0\\ \\&\Leftrightarrow&x=4\ \text{ ou }\ x=-5\end{array}$
Comme $4\ $ et $\ -5$ sont des éléments de $\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace 4\;;\ -5\right\rbrace}$
b) Soit à résoudre l'équation suivante : $\left(x+\dfrac{5}{3}\right)\left(x-\dfrac{3}{4}\right)=0$
On a :
$\begin{array}{rcl} \left(x+\dfrac{5}{3}\right)\left(x-\dfrac{3}{4}\right)=0&\Leftrightarrow&x+\dfrac{5}{3}=0\ \text{ ou }\ x-\dfrac{3}{4}=0\\ \\&\Leftrightarrow&x=-\dfrac{5}{3}\ \text{ ou }\ x=\dfrac{3}{4}\end{array}$
Comme $-\dfrac{5}{3}\ $ et $\ \dfrac{3}{4}$ sont des éléments de $\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace -\dfrac{5}{3}\;;\ \dfrac{3}{4}\right\rbrace}$
c) Soit à résoudre l'équation suivante : $(2x-1)(3x+4)=0$
Alors, on a :
$\begin{array}{rcl} (2x-1)(3x+4)=0&\Leftrightarrow&2x-1=0\ \text{ ou }\ 3x+4=0\\ \\&\Leftrightarrow&2x=1\ \text{ ou }\ 3x=-4\\\\&\Leftrightarrow&x=\dfrac{1}{2}\ \text{ ou }\ x=\dfrac{-4}{3}\end{array}$
Comme $\dfrac{1}{2}\ $ et $\ \dfrac{-4}{3}$ sont des éléments de $\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace \dfrac{1}{2}\;;\ \dfrac{-4}{3}\right\rbrace}$
d) Soit à résoudre l'équation suivante : $\left(3x-\dfrac{3}{4}\right)\left(2x-\dfrac{1}{3}\right)=0$
On a :
$\begin{array}{rcl} \left(3x-\dfrac{3}{4}\right)\left(2x-\dfrac{1}{3}\right)=0&\Leftrightarrow&3x-\dfrac{3}{4}=0\ \text{ ou }\ 2x-\dfrac{1}{3}=0\\ \\&\Leftrightarrow&3x=\dfrac{3}{4}\ \text{ ou }\ 2x=\dfrac{1}{3}\\\\&\Leftrightarrow&x=\dfrac{\dfrac{3}{4}}{3}\ \text{ ou }\ x=\dfrac{\dfrac{1}{3}}{2}\\\\&\Leftrightarrow&x=\dfrac{3}{4}\times\dfrac{1}{3}\ \text{ ou }\ x=\dfrac{1}{3}\times\dfrac{1}{2}\\\\&\Leftrightarrow&x=\dfrac{1}{4}\ \text{ ou }\ x=\dfrac{1}{6}\end{array}$
Comme $\dfrac{1}{4}\ $ et $\ \dfrac{1}{6}$ sont des éléments de $\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace \dfrac{1}{4}\;;\ \dfrac{1}{6}\right\rbrace}$
2) Résolvons dans $\mathbb{Q}$ chacune des équations suivantes.
On utilise la forme factorisée des identités remarquables.
a) Soit à résoudre l'équation suivante : $x^{2}-6x+9=0$
En factorisant l'expression $x^{2}-6x+9$, on obtient :
$$x^{2}-6x+9=(x-3)^{2}=(x-3)(x-3)$$
Par suite,
$\begin{array}{rcl} x^{2}-6x+9=0&\Leftrightarrow&(x-3)(x-3)=0\\\\&\Leftrightarrow&x-3=0\ \text{ ou }\ x-3=0\\ \\&\Leftrightarrow&x=3\ \text{ ou }\ x=3\end{array}$
Or, $3\in\mathbb{Q}\ $ donc, $\boxed{S=\left\lbrace 3\right\rbrace}$
b) Soit à résoudre l'équation suivante : $49x^{2}-1=0$
En factorisant l'expression $49x^{2}-1$, on obtient :
$$49x^{2}-1=(7x-1)(7x+1)$$
Ainsi,
$\begin{array}{rcl} 49x^{2}-1=0&\Leftrightarrow&(7x-1)(7x+1)=0\\\\&\Leftrightarrow&7x-1=0\ \text{ ou }\ 7x+1=0\\ \\&\Leftrightarrow&7x=1\ \text{ ou }\ 7x=-1\\\\&\Leftrightarrow&x=\dfrac{1}{7}\ \text{ ou }\ x=-\dfrac{1}{7}\end{array}$
Comme $\dfrac{1}{7}\ $ et $\ -\dfrac{1}{7}$ appartiennent à $\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace \dfrac{1}{7}\;;\ -\dfrac{1}{7}\right\rbrace}$
c) Soit à résoudre l'équation suivante : $4x^{2}+12x+9=0$
En factorisant l'expression $4x^{2}+12x+9$, on obtient :
$$4x^{2}+12x+9=(2x+3)^{2}=(2x+3)(2x+3)$$
Donc,
$\begin{array}{rcl} 4x^{2}+12x+9=0&\Leftrightarrow&(2x+3)(2x+3)=0\\\\&\Leftrightarrow&2x+3=0\ \text{ ou }\ 2x+3=0\\ \\&\Leftrightarrow&2x=-3\ \text{ ou }\ 2x=-3\\\\&\Leftrightarrow&x=-\dfrac{3}{2}\ \text{ ou }\ x=-\dfrac{3}{2}\end{array}$
Comme $-\dfrac{3}{2}\in\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace -\dfrac{3}{2}\right\rbrace}$
d) Soit à résoudre l'équation suivante : $36x^{2}-1=0$
En factorisant l'expression $36x^{2}-1$, on obtient :
$$36x^{2}-1=(6x-1)(6x+1)$$
Par suite,
$\begin{array}{rcl} 36x^{2}-1=0&\Leftrightarrow&(6x-1)(6x+1)=0\\\\&\Leftrightarrow&6x-1=0\ \text{ ou }\ 6x+1=0\\ \\&\Leftrightarrow&6x=1\ \text{ ou }\ 6x=-1\\\\&\Leftrightarrow&x=\dfrac{1}{6}\ \text{ ou }\ x=-\dfrac{1}{6}\end{array}$
Comme $\dfrac{1}{6}\ $ et $\ -\dfrac{1}{6}$ sont des éléments de $\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace \dfrac{1}{6}\;;\ -\dfrac{1}{6}\right\rbrace}$
e) Soit à résoudre l'équation suivante : $x^{2}-1=0$
En factorisant l'expression $x^{2}-1$, on obtient :
$$x^{2}-1=(x-1)(x+1)$$
Ainsi,
$\begin{array}{rcl} x^{2}-1=0&\Leftrightarrow&(x-1)(x+1)=0\\\\&\Leftrightarrow&x-1=0\ \text{ ou }\ x+1=0\\ \\&\Leftrightarrow&x=1\ \text{ ou }\ x=-1\end{array}$
Comme $1\ $ et $\ -1$ sont des éléments de $\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace 1\;;\ -1\right\rbrace}$
f) Soit à résoudre l'équation suivante : $4x^{2}-49=0$
En factorisant l'expression $4x^{2}-49$, on obtient :
$$4x^{2}-49=(2x-7)(2x+7)$$
Ainsi,
$\begin{array}{rcl} 4x^{2}-49=0&\Leftrightarrow&(2x-7)(2x+7)=0\\\\&\Leftrightarrow&2x-7=0\ \text{ ou }\ 2x+7=0\\ \\&\Leftrightarrow&2x=7\ \text{ ou }\ 2x=-7\\\\&\Leftrightarrow&x=\dfrac{7}{2}\ \text{ ou }\ x=-\dfrac{7}{2}\end{array}$
Comme $\dfrac{7}{2}\ $ et $\ -\dfrac{7}{2}$ appartiennent à $\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace \dfrac{7}{2}\;;\ -\dfrac{7}{2}\right\rbrace}$
3) Résolvons dans $\mathbb{Q}$ chacune des équations suivantes.
a) Soit à résoudre l'équation suivante : $(2x-1)(4x-3)-(2x-1)(6x-1)=0$
On factorise d'abord l'expression $(2x-1)(4x-3)-(2x-1)(6x-1)$
Ainsi, en mettant en évidence le facteur $(2x-1)$, on obtient :
$\begin{array}{rcl} (2x-1)(4x-3)-(2x-1)(6x-1)&=&(2x-1)[(4x-3)-(6x-1)]\\\\&=&(2x-1)(4x-3-6x+1)\\\\&=&(2x-1)(-2x-2)\end{array}$
Donc,
$$(2x-1)(4x-3)-(2x-1)(6x-1)=(2x-1)(-2x-2)$$
Par suite, en utilisant cette forme factorisée, on obtient :
$\begin{array}{rcl} (2x-1)(4x-3)-(2x-1)(6x-1)=0&\Leftrightarrow&(2x-1)(-2x-2)=0\\\\&\Leftrightarrow&2x-1=0\ \text{ ou }\ -2x-2=0\\ \\&\Leftrightarrow&2x=1\ \text{ ou }\ -2x=2\\\\&\Leftrightarrow&x=\dfrac{1}{2}\ \text{ ou }\ x=\dfrac{2}{-2}\\\\&\Leftrightarrow&x=\dfrac{1}{2}\ \text{ ou }\ x=-1\end{array}$
Comme $\dfrac{1}{2}\ $ et $\ -1$ appartiennent à $\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace \dfrac{1}{2}\;;\ -1\right\rbrace}$
b) Soit à résoudre l'équation suivante : $4x^{2}-1+(2x-1)(4x-5)=0$
En factorisant l'expression $4x^{2}-1+(2x-1)(4x-5)$, on obtient :
$\begin{array}{rcl} 4x^{2}-1+(2x-1)(4x-5)&=&(2x-1)(2x+1)+(2x-1)(4x-5)\\\\&=&(2x-1)[(2x+1)+(4x-5)]\\\\&=&(2x-1)(2x+1+4x-5)\\\\&=&(2x-1)(6x-4)\end{array}$
Ainsi,
$$4x^{2}-1+(2x-1)(4x-5)=(2x-1)(6x-4)$$
Par suite, en utilisant cette forme factorisée, on obtient :
$\begin{array}{rcl} 4x^{2}-1+(2x-1)(4x-5)=0&\Leftrightarrow&(2x-1)(6x-4)=0\\\\&\Leftrightarrow&2x-1=0\ \text{ ou }\ 6x-4=0\\ \\&\Leftrightarrow&2x=1\ \text{ ou }\ 6x=4\\\\&\Leftrightarrow&x=\dfrac{1}{2}\ \text{ ou }\ x=\dfrac{4}{6}\\\\&\Leftrightarrow&x=\dfrac{1}{2}\ \text{ ou }\ x=\dfrac{2}{3}\end{array}$
Comme $\dfrac{1}{2}\ $ et $\ \dfrac{2}{3}$ appartiennent à $\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace \dfrac{1}{2}\;;\ \dfrac{2}{3}\right\rbrace}$
c) Soit à résoudre l'équation suivante : $(3x-1)^{2}-(x-3)^{2}=0$
En factorisant l'expression $(3x-1)^{2}-(x-3)^{2}$, on obtient :
$\begin{array}{rcl} (3x-1)^{2}-(x-3)^{2}&=&[(3x-1)-(x-3)][(3x-1)+(x-3)]\\\\&=&(3x-1-x+3)(3x-1+x-3)\\\\&=&(2x+2)(4x-4)\end{array}$
Donc,
$$(3x-1)^{2}-(x-3)^{2}=(2x+2)(4x-4)$$
Par suite, en utilisant cette forme factorisée, on obtient :
$\begin{array}{rcl} (3x-1)^{2}-(x-3)^{2}=0&\Leftrightarrow&(2x+2)(4x-4)=0\\\\&\Leftrightarrow&2x+2=0\ \text{ ou }\ 4x-4=0\\ \\&\Leftrightarrow&2x=-2\ \text{ ou }\ 4x=4\\\\&\Leftrightarrow&x=\dfrac{-2}{2}\ \text{ ou }\ x=\dfrac{4}{4}\\\\&\Leftrightarrow&x=-1\ \text{ ou }\ x=1\end{array}$
Comme $-1\ $ et $\ 1$ appartiennent à $\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace -1\;;\ 1\right\rbrace}$
Exercice 8 "Équation de la forme $\dfrac{ax+b}{k}=\dfrac{cx+d}{k'}$"
Résolvons dans $\mathbb{Q}$ chacune des équations suivantes
En effet, résoudre les équations de la forme $\dfrac{ax+b}{k}=\dfrac{cx+d}{k'}$ revient à faire : produit des extrêmes $k'\times(ax+b)$ de cette égalité de quotients égal au produit de moyens $k\times(cx+d)$
Ainsi, pour résoudre une équation de la forme $\dfrac{ax+b}{k}=\dfrac{cx+d}{k'}$, il suffit de résoudre l'équation $k'\times(ax+b)=k\times(cx+d)\ :$
$$\dfrac{ax+b}{k}=\dfrac{cx+d}{k'}\ \Leftrightarrow\ k'\times(ax+b)=k\times(cx+d)$$
a) Soit à résoudre l'équation suivante : $\dfrac{x+1}{2}=\dfrac{2x-1}{3}$
Alors, on a :
$\begin{array}{rcl} \dfrac{x+1}{2}=\dfrac{2x-1}{3}&\Leftrightarrow&3(x+1)=2(2x-1)\\\\&\Leftrightarrow&3\times x+3\times 1=2\times(2x)-2\times 1\\ \\&\Leftrightarrow&3x+3=4x-2\\\\&\Leftrightarrow&3x-4x=-2-3\\\\&\Leftrightarrow&-x=-5\\\\&\Leftrightarrow&x=\dfrac{-5}{-1}\\\\&\Leftrightarrow&x=5\end{array}$
Comme $5\in\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace 5\right\rbrace}$
b) Soit à résoudre l'équation suivante : $\dfrac{x-1}{3}=\dfrac{7x-2}{5}$
$\begin{array}{rcl} \dfrac{x-1}{3}=\dfrac{7x-2}{5}&\Leftrightarrow&5(x-1)=3(7x-2)\\\\&\Leftrightarrow&5\times x-5\times 1=3\times(7x)-3\times 2\\ \\&\Leftrightarrow&5x-5=21x-6\\\\&\Leftrightarrow&5x-21x=-6+5\\\\&\Leftrightarrow&-16x=-1\\\\&\Leftrightarrow&x=\dfrac{-1}{-16}\\\\&\Leftrightarrow&x=\dfrac{1}{16}\end{array}$
Comme $\dfrac{1}{16}\in\mathbb{Q}\ $ alors, $\boxed{S=\left\lbrace \dfrac{1}{16}\right\rbrace}$
c) Soit à résoudre l'équation suivante : $\dfrac{4x-5}{3}+\dfrac{7x-2}{2}=0$
On peut commencer par changer de membre l'un des quotient en changeant son signe.
On obtient alors :
$$\dfrac{4x-5}{3}+\dfrac{7x-2}{2}=0\ \Leftrightarrow\ \dfrac{4x-5}{3}=-\dfrac{7x-2}{2}$$
Donc, résoudre l'équation $\dfrac{4x-5}{3}+\dfrac{7x-2}{2}=0$ revient à résoudre l'équation suivante : $\dfrac{4x-5}{3}=-\dfrac{7x-2}{2}$
Ainsi, on a :
$\begin{array}{rcl} \dfrac{4x-5}{3}+\dfrac{7x-2}{2}=0&\Leftrightarrow&\dfrac{4x-5}{3}=-\dfrac{7x-2}{2}\\\\&\Leftrightarrow&2(4x-5)=3[-(7x-2)]\\\\&\Leftrightarrow&2(4x-5)=3(-7x+2)\\\\&\Leftrightarrow&2\times(4x)-2\times 5=3\times(-7x)+3\times 2\\ \\&\Leftrightarrow&8x-10=-21x+6\\\\&\Leftrightarrow&8x+21x=6+10\\\\&\Leftrightarrow&29x=16\\\\&\Leftrightarrow&x=\dfrac{16}{29}\end{array}$
Or, $\dfrac{16}{29}\in\mathbb{Q}\ $ donc, $\boxed{S=\left\lbrace \dfrac{16}{29}\right\rbrace}$
d) Soit à résoudre l'équation suivante : $\dfrac{6x-1}{4}=-\dfrac{5x-1}{3}$
On a :
$\begin{array}{rcl} \dfrac{6x-1}{4}=-\dfrac{5x-1}{3}&\Leftrightarrow&3(6x-1)=4[-(5x-1)]\\\\&\Leftrightarrow&3(6x-1)=4(-5x+1)\\\\&\Leftrightarrow&3\times(6x)-3\times 1=4\times(-5x)+4\times 1\\ \\&\Leftrightarrow&18x-3=-20x+4\\\\&\Leftrightarrow&18x+20x=4+3\\\\&\Leftrightarrow&38x=7\\\\&\Leftrightarrow&x=\dfrac{7}{38}\end{array}$
Comme $\dfrac{7}{38}\in\mathbb{Q}\ $ donc, $\boxed{S=\left\lbrace \dfrac{7}{38}\right\rbrace}$
Exercice 9
Ndeuss a $15$ ans ; sa petite sœur Coumba a $6$ ans.
Déterminons le nombre d'années pour lequel l'âge de Neuss sera le double de sa sœur Coumba.
Soit $x$ le nombre d'années pour lequel l'âge de Neuss sera le double de sa sœur Coumba.
Alors, pour ce nombre $x$ d'années :
Ndeuss aura $15+x$ ans
Coumba aura $6+x$ ans
L'hypothèse suivante ; l'âge de Neuss sera le double de sa sœur Coumba peut se traduire sous forme d'équation par :
$$15+x=2(6+x)$$
En résolvant cette équation, on obtient :
$\begin{array}{rcl} 15+x=2(6+x)&\Leftrightarrow&15+x=2\times 6+2\times x\\ \\&\Leftrightarrow&15+x=12+2x\\\\&\Leftrightarrow&x-2x=12-15\\\\&\Leftrightarrow&-x=-3\\\\&\Leftrightarrow&x=\dfrac{-3}{-1}\\\\&\Leftrightarrow&x=3\end{array}$
Donc, dans $3$ ans l'âge de Neuss sera le double de sa sœur Coumba.
Vérification
On a :
$15+3=18$ donc, dans $3$ ans, Neuss aura $18$ ans.
$6+3=9$ donc, dans $3$ ans, sa sœur Coumba aura $9$ ans.
Or, $18=2\times 9$ donc, l'âge de Neuss est bien le double de celui de sa sœur Coumba.
Exercice 10
Adama, Assane et Abdou se partagent $79$ billes, Assane en a $2$ fois plus que Adama et Abdou en a $7$ de plus que Adama.
Déterminons la part de Adama, Assane et de Abdou.
Soit $x$ le nombre de billes dont dispose Adama.
On sait que Assane a $2$ fois plus que Adama.
Donc, la part de Assane est égale à : $2x$
Aussi, Abdou a $7$ billes de plus que Adama.
Donc, la part de Abdou est égale à : $x+7$
Par ailleurs, on sait que somme des parts est égale à $79$ billes.
Ce qui peut se traduire par l'équation suivante :
$$x+2x+(x+7)=79$$
En résolvant cette équation, on trouve la valeur de $x$ qui représente la part de Adama.
Ainsi, on a :
$\begin{array}{rcl} x+2x+(x+7)=79&\Leftrightarrow&x+2x+x+7=79\\ \\&\Leftrightarrow&4x=79-7\\\\&\Leftrightarrow&4x=72\\\\&\Leftrightarrow&x=\dfrac{72}{4}\\\\&\Leftrightarrow&x=18\end{array}$
Par suite, Adama dispose de $18$ billes
On a :
$2\times 18=36$ donc, Assane dispose de $36$ billes
$18+7=25$ alors, Abdou dispose de $25$ billes
Vérification :
On a : $18+36+25=79$
Ainsi, la somme des parts est bien égale à $79$ billes.
Exercice 11
Traduisons chacune des phrases suivantes par une équation.
1) La somme d'un nombre et de $7$ est égale à $5.$
Soit $x$ ce nombre, alors on a :
$$x+7=5$$
2) La différence d'un nombre et de $8$ est égale à $-3.$
Soit $x$ ce nombre, alors cette phrase se traduit par :
$$x-8=-3$$
3) Le produit d'un nombre et de $10$ est égal à $11.$
Soit $x$ ce nombre, alors cette phrase se traduit par :
$$x\times 10=11$$
4) Le quotient d'un nombre et de $4$ est égal à $5.$
Soit $x$ ce nombre, alors cette phrase se traduit par :
$$\dfrac{x}{4}=5$$
Exercice 12
1) Imaginons une équation du premier degré à une inconnue ayant pour solution $x=3.$
En faisant passer le nombre $3$ de la droite vers la gauche en changeant son signe, on obtient :
$$x-3=0$$
2) Imaginons une équation du premier degré à une inconnue ayant pour solution $t=-2.$
En faisant passer le nombre $-2$ de la droite vers la gauche en changeant son signe, on trouve :
$$t+2=0$$
Exercice 13
Khoudia dépense le quart de son salaire pour son logement et les deux cinquièmes pour la nourriture.
Il lui reste $227\,500\; F$ pour les autres dépenses.
Calculons son salaire mensuel.
Soit $x$ le salaire de Khoudia.
Alors :
la dépense pour le logement est égale à : $\dfrac{1}{4}x$
la dépense pour le nourriture est égale à : $\dfrac{2}{5}x$
les autres dépenses sont égales à : $227\,500\; F$
Or, on sait que la somme de toutes ces dépenses est égale au salaire $x.$
Ce qui se traduit par :
$$\dfrac{1}{4}x+\dfrac{2}{5}x+227\,500=x$$
On va résoudre cette équation pour trouver la valeur de $x$ qui détermine le salaire de Khoudia.
On a :
$\begin{array}{rcl} \dfrac{1}{4}x+\dfrac{2}{5}x+227\,500=x&\Leftrightarrow&\dfrac{1}{4}x+\dfrac{2}{5}x-x=-227\,500\\ \\&\Leftrightarrow&\dfrac{5}{20}x+\dfrac{8}{20}x-\dfrac{20}{20}x=-227\,500\\\\&\Leftrightarrow&-\dfrac{7}{20}x=-227\,500\\\\&\Leftrightarrow&x=\dfrac{-227\,500}{-\dfrac{7}{20}}\\\\&\Leftrightarrow&x=-227\,500\times\left(-\dfrac{20}{7}\right)\\\\&\Leftrightarrow&x=\dfrac{4\,550\,000}{7}\\\\&\Leftrightarrow&x=650\,000\end{array}$
Donc, Khoudia a un salaire de : $650\,000\; F$
Par suite,
pour le logement, on a : $\dfrac{650\,000}{4}=162\,500$ donc, Khoudia dépense $162\,500\;F$ pour son logement.
pour la nourriture, on a : $\dfrac{2\times 650\,000}{5}=260\,000$ alors, Khoudia dépense $260\,000\;F$ pour la nourriture.
Vérification :
On a : $162\,500\;F+260\,000\;F+227\,500\;F=650\,000\;F$
Ce qui prouve que la somme de toutes ses dépenses est égale à son salaire.
Exercice 14 Problème
On donne $f(x)=4x^{2}-1-(1-2x)(3x+4).$
1) a) Nous allons développer, réduire et ordonner $f(x).$
On a :
$\begin{array}{rcl} f(x)&=&4x^{2}-1-(1-2x)(3x+4)\\\\&=&4x^{2}-1+(-1+2x)(3x+4)\\\\&=&4x^{2}-1-1\times(3x)-1\times 4+(2x)\times(3x)+(2x)\times 4\\\\&=&4x^{2}-1-3x-4+6x^{2}+8x\\\\&=&4x^{2}+6x^{2}-3x+8x-1-4\\\\&=&10x^{2}+5x-5\end{array}$
D'où, $\boxed{f(x)=10x^{2}+5x-5}$
b) Calculons $f(0).$
Considérons la forme développée de $f(x)$ et remplaçons $x$ par $0.$
Soit : $f(x)=10x^{2}+5x-5$
Alors,
$\begin{array}{rcl} f(0)&=&10\times(0)^{2}+5\times 0-5\\\\&=&-5\end{array}$
Ainsi, $\boxed{f(0)=-5}$
2) a) Factorisons $f(x).$
Soit : $f(x)=4x^{2}-1-(1-2x)(3x+4)$
Dans l'expression de $f(x)$ on peut identifier deux parties $4x^{2}-1\ $ et $\ -(1-2x)(3x+4).$
Or, en utilisant la propriété des identités remarquables $a^{2}-b^{2}=(a-b)(a+b)$, on peut écrire :
$$4x^{2}-1=(2x-1)(2x+1)$$
De plus, en appliquant la règle sur le signe $(-)$ devant une parenthèse, on obtient :
$$-(1-2x)(3x+4)=(-1+2x)(3x+4)=(2x-1)(3x+4)$$
Finalement, en remplaçant les expressions de $4x^{2}-1\ $ et $\ -(1-2x)(3x+4)$ dans celle de $f(x)$, on obtient :
$$f(x)=(2x-1)(2x+1)+(2x-1)(3x+4)$$
En mettant en évidence le facteur commun $(2x-1)$, on obtient :
$\begin{array}{rcl} f(x)&=&(2x-1)(2x+1)+(2x-1)(3x+4)\\\\&=&(2x-1)[(2x+1)+(3x+4)]\\\\&=&(2x-1)(2x+1+3x+4)\\\\&=&(2x-1)(5x+5)\end{array}$
D'où, $\boxed{f(x)=(2x-1)(5x+5)}$
b) Résolvons dans $\mathbb{Q}$ l'équation $f(x)=0$
Comme le second membre de cette équation est égal à $0$ alors, nous allons utiliser la forme factorisée de $f(x)$ pour résoudre l'équation $f(x)=0.$
On a :
$\begin{array}{rcl} f(x)=0&\Leftrightarrow&(2x-1)(5x+5)=0\\\\&\Leftrightarrow&2x-1=0\ \text{ ou }\ 5x+5=0\\ \\&\Leftrightarrow&2x=1\ \text{ ou }\ 5x=-5\\\\&\Leftrightarrow&x=\dfrac{1}{2}\ \text{ ou }\ x=\dfrac{-5}{5}\\\\&\Leftrightarrow&x=\dfrac{1}{2}\ \text{ ou }\ x=-1\end{array}$
Comme $-1\ $ et $\ \dfrac{1}{2}$ appartiennent à $\mathbb{Q}$ alors,
$$\boxed{S=\left\lbrace -1\;;\ \dfrac{1}{2}\right\rbrace}$$
Exercice 15 Problème
On considère les expressions suivantes :
$f(x)=(5x-2)^{2}-(2x+3)^{2}\;;\quad g(x)=(3x-5)(2x-1)+9x^{2}-30x+25.$
1) Nous allons développer, réduire et ordonner $f(x)\ $ et $\ g(x).$
On a :
$\begin{array}{rcl} f(x)&=&(5x-2)^{2}-(2x+3)^{2}\\\\&=&(5x)^{2}-2\times 2\times(5x)+2^{2}-[(2x)^{2}+2\times 3\times(2x)+3^{2}]\\\\&=&25x^{2}-20x+4-(4x^{2}+12x+9)\\\\&=&25x^{2}-20x+4-4x^{2}-12x-9\\\\&=&25x^{2}-4x^{2}-20x-12x+4-9\\\\&=&21x^{2}-32x-5\end{array}$
D'où, $\boxed{f(x)=21x^{2}-32x-5}$
On a :
$\begin{array}{rcl} g(x)&=&(3x-5)(2x-1)+9x^{2}-30x+25\\\\&=&(3x)\times(2x)+(3x)\times(-1)-5\times(2x)-5\times(-1)+9x^{2}-30x+25\\\\&=&6x^{2}-3x-10x+5+9x^{2}-30x+25\\\\&=&6x^{2}+9x^{2}-3x-10x-30x+5+25\\\\&=&15x^{2}-43x+30\end{array}$
Ainsi, $\boxed{g(x)=15x^{2}-43x+30}$
2) Factorisons $f(x)\ $ et $\ g(x)$ en déduisons le facteur commun de $f(x)\ $ et $\ g(x).$
Soit $f(x)=(5x-2)^{2}-(2x+3)^{2}$ alors, $f(x)$ est de la forme $a^{2}-b^{2}.$
Donc, en appliquant la propriété des identités remarquables, on obtient :
$\begin{array}{rcl} f(x)&=&(5x-2)^{2}-(2x+3)^{2}\\\\&=&[(5x-2)-(2x+3)][(5x-2)+(2x+3)]\\\\&=&(5x-2-2x-3)(5x-2+2x+3)\\\\&=&(5x-2x-2-3)(5x+2x-2+3)\\\\&=&(3x-5)(7x+1)\end{array}$
Par suite, $\boxed{f(x)=(3x-5)(7x+1)}$
Soit $g(x)=(3x-5)(2x-1)+9x^{2}-30x+25$
Alors, on factorise d'abord la partie $9x^{2}-30x+25$ en utilisant la propriété des identités remarquables.
Ce qui donne :
$$9x^{2}-30x+25=(3x-5)^{2}$$
En remplaçant dans l'expression de $g(x)$, on obtient :
$$g(x)=(3x-5)(2x-1)+(3x-5)^{2}$$
On reconnait alors un facteur commun ; $(3x-5)$
Par suite,
$\begin{array}{rcl} g(x)&=&(3x-5)(2x-1)+(3x-5)^{2}\\\\&=&(3x-5)[(2x-1)+(3x-5)]\\\\&=&(3x-5)(2x-1+3x-5)\\\\&=&(3x-5)(2x+3x-1-5)\\\\&=&(3x-5)(5x-6)\end{array}$
D'où, $\boxed{g(x)=(3x-5)(5x-6)}$
On a : $f(x)=(3x-5)(7x+1)\ $ et $\ g(x)=(3x-5)(5x-6)$
Donc, le facteur commun de $f(x)\ $ et $\ g(x)$ est :
$$(3x-5)$$
3) Résolvons dans $\mathbb{Q}$ les équations suivantes : $f(x)=0\ $ et $\ g(x)=0.$
Comme le second membre de ces équations est égal à $0$ alors, nous allons considérer les formes factorisées de $f(x)$ et de $g(x)$ pour résoudre les équations $f(x)=0\ $ et $\ g(x)=0.$
Soit $f(x)=(3x-5)(7x+1)$ alors, on a :
$\begin{array}{rcl} f(x)=0&\Leftrightarrow&(3x-5)(7x+1)\\\\&\Leftrightarrow&3x-5=0\ \text{ ou }\ 7x+1=0\\ \\&\Leftrightarrow&3x=5\ \text{ ou }\ 7x=-1\\\\&\Leftrightarrow&x=\dfrac{5}{3}\ \text{ ou }\ x=\dfrac{-1}{7}\end{array}$
Comme $\dfrac{-1}{7}\ $ et $\ \dfrac{5}{3}$ appartiennent à $\mathbb{Q}$ alors,
$$\boxed{S=\left\lbrace \dfrac{-1}{7}\;;\ \dfrac{5}{3}\right\rbrace}$$
Soit $g(x)=(3x-5)(5x-6)$ alors, on a :
$\begin{array}{rcl} g(x)=0&\Leftrightarrow&(3x-5)(5x-6)\\\\&\Leftrightarrow&3x-5=0\ \text{ ou }\ 5x-6=0\\ \\&\Leftrightarrow&3x=5\ \text{ ou }\ 5x=6\\\\&\Leftrightarrow&x=\dfrac{5}{3}\ \text{ ou }\ x=\dfrac{6}{5}\end{array}$
Comme $\dfrac{5}{3}\ $ et $\ \dfrac{6}{5}$ appartiennent à $\mathbb{Q}$ alors,
$$\boxed{S=\left\lbrace \dfrac{5}{3}\;;\ \dfrac{6}{5}\right\rbrace}$$
4) Résolvons dans $\mathbb{Q}$ les équations suivantes : $f(x)=21x^{2}\ $ et $\ g(x)=15x^{2}.$
Comme le second membre de ces équations est différent de $0$ alors, nous allons utiliser les formes développées de $f(x)$ et de $g(x)$ pour résoudre les équations $f(x)=21x^{2}\ $ et $\ g(x)=15x^{2}.$
Soit $f(x)=21x^{2}-32x-5$ alors, on a :
$\begin{array}{rcl} f(x)=21x^{2}&\Leftrightarrow&21x^{2}-32x-5=21x^{2}\\\\&\Leftrightarrow&21x^{2}-32x-21x^{2}=5\\ \\&\Leftrightarrow&21x^{2}-21x^{2}-32x=5\\\\&\Leftrightarrow&-32x=5\\\\&\Leftrightarrow&x=\dfrac{5}{-32}\end{array}$
Or, $\dfrac{5}{-32}\in\mathbb{Q}$ donc,
$$\boxed{S=\left\lbrace \dfrac{5}{-32}\right\rbrace}$$
Soit $g(x)=15x^{2}-43x+30$ alors, on a :
$\begin{array}{rcl} g(x)=15x^{2}&\Leftrightarrow&15x^{2}-43x+30=15x^{2}\\\\&\Leftrightarrow&15x^{2}-43x-15x^{2}=-30\\ \\&\Leftrightarrow&15x^{2}-15x^{2}-43x=-30\\\\&\Leftrightarrow&-43x=-30\\\\&\Leftrightarrow&x=\dfrac{-30}{-43}\\\\&\Leftrightarrow&x=\dfrac{30}{43}\end{array}$
Comme $\dfrac{30}{43}\in\mathbb{Q}$ alors,
$$\boxed{S=\left\lbrace \dfrac{30}{43}\right\rbrace}$$
Exercice 16 Problème et Identités remarquables
On considère les expressions suivantes.
$A(x)=(2x-1)^{2}+2(2x-1)(7x-1)+(7x-1)^{2}.$
$B(x)=(x-1)^{2}-2(x-1)(3x-1)+(3x-1)^{2}.$
$C(x)=x^{2}+2x(8x-1)+(8x-1)^{2}.$
1) Développons, réduisons et ordonnons les expressions suivantes : $A(x)\;;\ B(x)\ $ et $\ C(x).$
On a :
$\begin{array}{rcl} A(x)&=&(2x-1)^{2}+2(2x-1)(7x-1)+(7x-1)^{2}\\\\&=&4x^{2}-4x+1+2(14x^{2}-2x-7x+1)+49x^{2}-14x+1\\\\&=&4x^{2}-4x+1+28x^{2}-4x-14x+2+49x^{2}-14x+1\\\\&=&4x^{2}+28x^{2}+49x^{2}-4x-4x-14x-14x+1+2+1\\\\&=&81x^{2}-36x+4\end{array}$
D'où, $\boxed{A(x)=81x^{2}-36x+4}$
On a :
$\begin{array}{rcl} B(x)&=&(x-1)^{2}-2(x-1)(3x-1)+(3x-1)^{2}\\\\&=&x^{2}-2x+1-2(3x^{2}-x-3x+1)+9x^{2}-6x+1\\\\&=&x^{2}-2x+1-6x^{2}+2x+6x-2+9x^{2}-6x+1\\\\&=&x^{2}-6x^{2}+9x^{2}-2x+2x+6x-6x+1-2+1\\\\&=&4x^{2}\end{array}$
Donc, $\boxed{B(x)=4x^{2}}$
On a :
$\begin{array}{rcl} C(x)&=&x^{2}+2x(8x-1)+(8x-1)^{2}\\\\&=&x^{2}+16x^{2}-2x+64x^{2}-16x+1\\\\&=&x^{2}+16x^{2}+64x^{2}-2x-16x+1\\\\&=&81x^{2}-18x+1\end{array}$
Ainsi, $\boxed{C(x)=81x^{2}-18x+1}$
2) Factorisons les expressions : $A(x)\;;\ B(x)\ $ et $\ C(x).$
Soit $A(x)=(2x-1)^{2}+2(2x-1)(7x-1)+(7x-1)^{2}$ alors, on constate que $A(x)$ est de la forme $a^{2}+2ab+b^{2}$ avec : $a=(2x-1)\ $ et $\ b=(7x-1)$
Donc, en utilisant la forme factorisée des identités remarquables $a^{2}+2ab+b^{2}=(a+b)^{2}$, on obtient :
$\begin{array}{rcl} A(x)&=&(2x-1)^{2}+2(2x-1)(7x-1)+(7x-1)^{2}\\\\&=&[(2x-1)+(7x-1)]^{2}\\\\&=&(2x-1+7x-1)^{2}\\\\&=&(2x+7x-1-1)^{2}\\\\&=&(9x-2)^{2}\end{array}$
D'où, $\boxed{A(x)=(9x-2)^{2}}$
Soit $B(x)=(x-1)^{2}-2(x-1)(3x-1)+(3x-1)^{2}.$
Alors, on remarque que $B(x)$ est de la forme $a^{2}-2ab+b^{2}$ avec : $a=(x-1)\ $ et $\ b=(3x-1).$
Donc, en utilisant la forme factorisée des identités remarquables $a^{2}-2ab+b^{2}=(a-b)^{2}$, on obtient :
$\begin{array}{rcl} B(x)&=&(x-1)^{2}-2(x-1)(3x-1)+(3x-1)^{2}\\\\&=&[(x-1)-(3x-1)]^{2}\\\\&=&(x-1-3x+1)^{2}\\\\&=&(x-3x-1+1)^{2}\\\\&=&(-2x)^{2}\end{array}$
Ainsi, $\boxed{B(x)=(-2x)^{2}}$
Soit $C(x)=x^{2}+2x(8x-1)+(8x-1)^{2}.$
Alors, on remarque que $C(x)$ est de la forme $a^{2}+2ab+b^{2}$ avec : $a=x\ $ et $\ b=(8x-1).$
Donc, en utilisant la forme factorisée des identités remarquables $a^{2}+2ab+b^{2}=(a+b)^{2}$, on obtient :
$\begin{array}{rcl} C(x)&=&x^{2}+2x(8x-1)+(8x-1)^{2}\\\\&=&[(x+(8x-1)]^{2}\\\\&=&(x+8x-1)^{2}\\\\&=&(9x-1)^{2}\end{array}$
D'où, $\boxed{C(x)=(9x-1)^{2}}$
3) Résolvons dans $\mathbb{Q}$ les équations suivantes : $A(x)=0\;;\ B(x)=0\ $ et $\ C(x)=81x^{2}.$
Comme le second membre des équations $A(x)=0\ $et $\ B(x)=0$ est égal à $0$ alors, nous allons considérer les formes factorisées de $A(x)$ et de $B(x)$ pour résoudre les équations $A(x)=0\ $ et $\ B(x)=0.$
Soit $A(x)=(9x-2)^{2}$ alors, on a :
$\begin{array}{rcl} A(x)=0&\Leftrightarrow&(9x-2)^{2}=0\\\\&\Leftrightarrow&9x-2=0\\ \\&\Leftrightarrow&9x=2\\\\&\Leftrightarrow&x=\dfrac{2}{9}\end{array}$
Comme $\dfrac{2}{9}\in\mathbb{Q}$ alors,
$$\boxed{S=\left\lbrace \dfrac{2}{9}\right\rbrace}$$
Soit $B(x)=(-2x)^{2}$ alors, on a :
$\begin{array}{rcl} B(x)=0&\Leftrightarrow&(-2x)^{2}=0\\\\&\Leftrightarrow&-2x=0\\ \\&\Leftrightarrow&x=\dfrac{0}{-2}\\\\&\Leftrightarrow&x=0\end{array}$
Comme $0$ est un élément de $\mathbb{Q}$ alors,
$$\boxed{S=\left\lbrace 0\right\rbrace}$$
$\ C(x)=81x^{2}.$
Pour résoudre l'équation $C(x)=81x^{2}$, nous pouvons utiliser la forme développée de $C(x)$ car le second membre de cette équation est différent de $0.$
Soit $C(x)=81x^{2}-18x+1$ alors, on a :
$\begin{array}{rcl} C(x)=81x^{2}&\Leftrightarrow&81x^{2}-18x+1=81x^{2}\\\\&\Leftrightarrow&81x^{2}-18x-81x^{2}=-1\\ \\&\Leftrightarrow&81x^{2}-81x^{2}-18x=-1\\\\&\Leftrightarrow&-18x=-1\\\\&\Leftrightarrow&x=\dfrac{-1}{-18}\\\\&\Leftrightarrow&x=\dfrac{1}{18}\end{array}$
Comme $\dfrac{1}{18}\in\mathbb{Q}$ alors,
$$\boxed{S=\left\lbrace \dfrac{1}{18}\right\rbrace}$$
Exercice 17 Problème
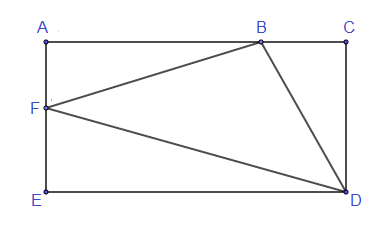
Le rectangle ci-dessous a pour longueur $AC=7\;cm$ et pour largeur $CD=4\;cm.\ B\in[AC]$ tel que $BC=x\;;\ F\in[AE]$ tel que $FE=x.$

1) Calculons l'aire du rectangle $ACDE.$
Soit $\mathcal{A}_{_{ACDE}}$ l'aire du rectangle $ACDE$ alors, on a :
$\begin{array}{rcl} \mathcal{A}_{_{ACDE}}&=&AC\times CD\\\\&=&7\times 4\\\\&=&28\end{array}$
Donc, $\boxed{\mathcal{A}_{_{ACDE}}=28\;cm^{2}}$
2) Calculons les aires des triangles $BCD\ $ et $\ DEF$ en fonction de $x.$
Soit $\mathcal{A}_{_{BCD}}$ l'aire du triangle $BCD$ alors, on a :
Comme le triangle $BCD$ est rectangle en $C$, alors on a :
$\begin{array}{rcl} \mathcal{A}_{_{BCD}}&=&\dfrac{CD\times BC}{2}\\\\&=&\dfrac{4\times x}{2}\\\\&=&2x\end{array}$
Par suite, $\boxed{\mathcal{A}_{_{BCD}}=2x\;cm^{2}}$
Soit $\mathcal{A}_{_{DEF}}$ l'aire du triangle $DEF.$
Comme le triangle $DEF$ est rectangle en $E$, alors on a :
$$\mathcal{A}_{_{DEF}}=\dfrac{ED\times FE}{2}$$
Or, $ED=AC$ car $ACDE$ est un rectangle.
Donc, en remplaçant $ED$ par $AC$, on obtient :
$\begin{array}{rcl} \mathcal{A}_{_{DEF}}&=&\dfrac{ED\times FE}{2}\\\\&=&\dfrac{AC\times FE}{2}\\\\&=&\dfrac{7\times x}{2}\\\\&=&\dfrac{7}{2}x\\\\&=&3.5x\end{array}$
D'où, $\boxed{\mathcal{A}_{_{DEF}}=3.5x\;cm^{2}}$
3) Montrons que l'aire du triangle $ABF$ est de : $$0.5x^{2}-5.5x+14$$
Soit $\mathcal{A}_{_{ABF}}$ l'aire du triangle $ABF.$
Le triangle $ABF$ étant rectangle en $A$, alors on a :
$$\mathcal{A}_{_{ABF}}=\dfrac{AB\times AF}{2}$$
Or, $B\in[AC]$ donc, $AB+BC=AC$
Par suite, $AB=AC-BC=7-x$
Aussi, comme $F\in[AE]$ alors, $AF+FE=AE$
Ainsi, $AF=AE-FE$
Or, $ACDE$ rectangle donc, $AE=CD$
Par suite, $AF=AE-FE=CD-FE=4-x$
En remplaçant $AB$ par $7-x\ $ et $\ AF$ par $4-x$ dans l'expression de $\mathcal{A}_{_{ABF}}$, on obtient :
$\begin{array}{rcl} \mathcal{A}_{_{ABF}}&=&\dfrac{AB\times AF}{2}\\\\&=&\dfrac{(7-x)(4-x)}{2}\\\\&=&\dfrac{7\times 4-7\times x-x\times 4-x\times(-x)}{2}\\\\&=&\dfrac{28-7x-4x+x^{2}}{2}\\\\&=&\dfrac{28-11x+x^{2}}{2}\\\\&=&\dfrac{28}{2}-\dfrac{11}{2}x+\dfrac{1}{2}x^{2}\\\\&=&14-5.5x+0.5x^{2}\\\\&=&0.5x^{2}-5.5x+14\end{array}$
D'où, $\boxed{\mathcal{A}_{_{ABF}}=0.5x^{2}-5.5x+14}$
4) En déduisons que l'aire de $FBD$ est égale à $-0.5x^{2}+14$
On sait que la somme des aires des triangles $BCD\;;\ DEF\;;\ ABF\ $ et $\ FBD$ est égale à l'aire du rectangle $ACDE.$
Ce qui peut encore s'écrire :
$$\mathcal{A}_{_{BCD}}+\mathcal{A}_{_{DEF}}+\mathcal{A}_{_{ABF}}+\mathcal{A}_{_{FBD}}=\mathcal{A}_{_{ACDE}}$$
Par suite,
$\begin{array}{rcl} \mathcal{A}_{_{FBD}}&=&\mathcal{A}_{_{ACDE}}-\mathcal{A}_{_{BCD}}-\mathcal{A}_{_{DEF}}-\mathcal{A}_{_{ABF}}\\\\&=&28-2x-3.5x-(0.5x^{2}-5.5x+14)\\\\&=&28-2x-3.5x-0.5x^{2}+5.5x-14\\\\&=&-0.5x^{2}-2x-3.5x+5.5x+28-14\\\\&=&-0.5x^{2}+14\end{array}$
D'où, $\boxed{\mathcal{A}_{_{FBD}}=-0.5x^{2}+14}$
5) Déterminons pour quelle valeur de $x$ l'aire du triangle $FBD$ représente les $\dfrac{3}{7}$ de l'aire du rectangle $ACDE.$
On a : $\mathcal{A}_{_{FBD}}=-0.5x^{2}+14\ $ et $\ \mathcal{A}_{_{ACDE}}=28$
Alors, l'aire du triangle $FBD$ représente les $\dfrac{3}{7}$ de l'aire du rectangle $ACDE$ peut se traduire par :
$$-0.5x^{2}+14=\dfrac{3}{7}\times 28=12$$
En résolvant cette équation, on trouve cette valeur de $x.$
Ainsi,
$\begin{array}{rcl} \mathcal{A}_{_{FBD}}=\dfrac{3}{7}\mathcal{A}_{_{ACDE}}&\Leftrightarrow&-0.5x^{2}+14=12\\\\&\Leftrightarrow&-0.5x^{2}+14=12-14\\ \\&\Leftrightarrow&-0.5x^{2}=-2\\\\&\Leftrightarrow&x^{2}=\dfrac{-2}{-0.5}\\\\&\Leftrightarrow&x^{2}=4\\\\&\Leftrightarrow&x^{2}-4=0\\\\&\Leftrightarrow&(x-2)(x+2)=0\\\\&\Leftrightarrow&x-2=0\ \text{ ou }\ x+2=0\\ \\&\Leftrightarrow&x=2\ \text{ ou }\ x=-2\end{array}$
On constate qu'on a deux valeurs de $x\ : 2\ $ et $\ -2$
Mais $x$ représente la distance $BC\ $ et $\ FE$ et une distance n'est jamais négative donc, nous allons considérer la valeur positive.
D'où, la valeur pour laquelle $\mathcal{A}_{_{FBD}}=\dfrac{3}{7}\mathcal{A}_{_{ACDE}}$ est : $2$
Exercice 19
Résolvons dans $\mathbb{Q}$ les équations ci-dessous.
Soit $5n-\dfrac{3}{2}=n+\dfrac{1}{6}$
Alors, on a :
$\begin{array}{rcl} 5n-\dfrac{3}{2}=n+\dfrac{1}{6}&\Leftrightarrow&5n-n=\dfrac{1}{6}+\dfrac{3}{2}\\\\&\Leftrightarrow&4n=\dfrac{1}{6}+\dfrac{9}{6}\\ \\&\Leftrightarrow&4n=\dfrac{10}{6}\\\\&\Leftrightarrow&n=\dfrac{\dfrac{10}{6}}{4}\\\\&\Leftrightarrow&n=\dfrac{10}{6}\times\dfrac{1}{4}\\\\&\Leftrightarrow&n=\dfrac{10}{24}\end{array}$
Comme $\dfrac{10}{24}\in\mathbb{Q}\ $ alors,
$$\boxed{S=\left\lbrace\dfrac{10}{24}\right\rbrace}$$
Soit $\dfrac{3m}{7}+2=5-\dfrac{m}{14}$ alors, on a :
$\begin{array}{rcl} \dfrac{3m}{7}+2=5-\dfrac{m}{14}&\Leftrightarrow&\dfrac{3m}{7}+\dfrac{m}{14}=5-2\\\\&\Leftrightarrow&\dfrac{6m}{14}+\dfrac{m}{14}=3\\ \\&\Leftrightarrow&\dfrac{7m}{14}=3\\\\&\Leftrightarrow&\dfrac{7m}{14}=\dfrac{3}{1}\\\\&\Leftrightarrow&1\times(7m)=3\times 14\\\\&\Leftrightarrow&7m=42\\\\&\Leftrightarrow&m=\dfrac{42}{7}\\\\&\Leftrightarrow&m=6\end{array}$
Comme $6$ est un élément de $\mathbb{Q}$ alors,
$$\boxed{S=\left\lbrace 6\right\rbrace}$$
Soit $-\dfrac{5}{3}+7x+1=\dfrac{x}{2}-1$ alors, on a :
$\begin{array}{rcl} -\dfrac{5}{3}+7x+1=\dfrac{x}{2}-1&\Leftrightarrow&7x-\dfrac{x}{2}=-1-1+\dfrac{5}{3}\\\\&\Leftrightarrow&\dfrac{14x}{2}-\dfrac{x}{2}=-2+\dfrac{5}{3}\\ \\&\Leftrightarrow&\dfrac{13x}{2}=\dfrac{-6}{3}+\dfrac{5}{3}\\\\&\Leftrightarrow&\dfrac{13x}{2}=\dfrac{-1}{3}\\\\&\Leftrightarrow&3\times(13x)=-1\times 2\\\\&\Leftrightarrow&39x=-2\\\\&\Leftrightarrow&x=\dfrac{-2}{39}\end{array}$
Comme $\dfrac{-2}{39}$ appartient à $\mathbb{Q}$ alors,
$$\boxed{S=\left\lbrace \dfrac{-2}{39}\right\rbrace}$$
Soit $\dfrac{2}{5}\left(\dfrac{2}{5}x+5\right)=-\dfrac{1}{2}\left(1-\dfrac{9}{5}x\right)$ alors, on a :
$\begin{array}{rcl} \dfrac{2}{5}\left(\dfrac{2}{5}x+5\right)=-\dfrac{1}{2}\left(1-\dfrac{9}{5}x\right)&\Leftrightarrow&\dfrac{2}{5}\times\left(\dfrac{2}{5}x\right)+\dfrac{2}{5}\times 5=-\dfrac{1}{2}\times 1-\dfrac{1}{2}\times\left(-\dfrac{9}{5}x\right)\\\\&\Leftrightarrow&\dfrac{4}{25}x+\dfrac{10}{5}=-\dfrac{1}{2}+\dfrac{9}{10}x\\ \\&\Leftrightarrow&\dfrac{4}{25}x-\dfrac{9}{10}x=-\dfrac{1}{2}-\dfrac{10}{5}\\\\&\Leftrightarrow&\dfrac{8}{50}x-\dfrac{45}{50}x=-\dfrac{5}{10}-\dfrac{20}{10}\\\\&\Leftrightarrow&-\dfrac{37}{50}x=-\dfrac{25}{10}\\\\&\Leftrightarrow&x=\dfrac{-\dfrac{25}{10}}{-\dfrac{37}{50}}\\\\&\Leftrightarrow&x=-\dfrac{25}{10}\times\left(-\dfrac{50}{37}\right)\\\\&\Leftrightarrow&x=\dfrac{1250}{370}\end{array}$
Comme $\dfrac{1250}{370}\in\mathbb{Q}$ alors,
$$\boxed{S=\left\lbrace \dfrac{1250}{370}\right\rbrace}$$
Exercice 20
Résolvons dans $\mathbb{Q}$ les équations ci-dessous
Soit $\dfrac{n}{2}-\dfrac{1}{3}\left(\dfrac{1}{2}-n\right)=\dfrac{7}{6}n+\dfrac{2}{3}$ alors, on a :
$\begin{array}{rcl} \dfrac{n}{2}-\dfrac{1}{3}\left(\dfrac{1}{2}-n\right)=\dfrac{7}{6}n+\dfrac{2}{3}&\Leftrightarrow&\dfrac{n}{2}-\dfrac{1}{3}\times\dfrac{1}{2}-\dfrac{1}{3}\times(-n)=\dfrac{7}{6}n+\dfrac{2}{3}\\\\&\Leftrightarrow&\dfrac{1}{2}n-\dfrac{1}{6}+\dfrac{1}{3}n=\dfrac{7}{6}n+\dfrac{2}{3}\\ \\&\Leftrightarrow&\dfrac{1}{2}n+\dfrac{1}{3}n-\dfrac{7}{6}n=\dfrac{2}{3}+\dfrac{1}{6}\\\\&\Leftrightarrow&\dfrac{3}{6}n+\dfrac{2}{6}n-\dfrac{7}{6}n=\dfrac{4}{6}+\dfrac{1}{6}\\\\&\Leftrightarrow&-\dfrac{2}{6}n=\dfrac{5}{6}\\\\&\Leftrightarrow&n=\dfrac{\dfrac{5}{6}}{-\dfrac{2}{6}}\\\\&\Leftrightarrow&n=\dfrac{5}{6}\times\left(-\dfrac{6}{2}\right)\\\\&\Leftrightarrow&n=-\dfrac{5\times 6}{6\times 2}\\\\&\Leftrightarrow&n=-\dfrac{5}{2}\end{array}$
Comme $-\dfrac{5}{2}\in\mathbb{Q}$ alors,
$$\boxed{S=\left\lbrace -\dfrac{5}{2}\right\rbrace}$$
Soit $2t-\dfrac{1}{4}=\dfrac{t}{2}$ alors, on a :
$\begin{array}{rcl} 2t-\dfrac{1}{4}=\dfrac{t}{2}&\Leftrightarrow&2t-\dfrac{t}{2}=\dfrac{1}{4}\\\\&\Leftrightarrow&\dfrac{4t}{2}-\dfrac{t}{2}=\dfrac{1}{4}\\ \\&\Leftrightarrow&\dfrac{3t}{2}=\dfrac{1}{4}\\\\&\Leftrightarrow&4\times(3t)=2\times 1\\\\&\Leftrightarrow&12t=2\\\\&\Leftrightarrow&t=\dfrac{2}{12}\end{array}$
Comme $\dfrac{2}{12}\in\mathbb{Q}$ alors,
$$\boxed{S=\left\lbrace \dfrac{2}{12}\right\rbrace}$$
Soit à résoudre l'équation $\dfrac{m}{3}=m-10.$
On a :
$\begin{array}{rcl} \dfrac{m}{3}=m-10&\Leftrightarrow&\dfrac{m}{3}-m=-10\\\\&\Leftrightarrow&\dfrac{m}{3}-\dfrac{3m}{3}=-10\\ \\&\Leftrightarrow&\dfrac{-2m}{3}=-10\\\\&\Leftrightarrow&\dfrac{-2m}{3}=\dfrac{-10}{1}\\\\&\Leftrightarrow&1\times(-2m)=3\times(-10)\\\\&\Leftrightarrow&-2m=-30\\\\&\Leftrightarrow&m=\dfrac{-30}{-2}\\\\&\Leftrightarrow&m=15\end{array}$
Comme $15\in\mathbb{Q}$ alors,
$$\boxed{S=\left\lbrace 15\right\rbrace}$$
Soit $3x=\dfrac{x}{3}+8$ alors, on a :
$\begin{array}{rcl} 3x=\dfrac{x}{3}+8&\Leftrightarrow&3x-\dfrac{x}{3}=8\\\\&\Leftrightarrow&\dfrac{9x}{3}-\dfrac{x}{3}=8\\ \\&\Leftrightarrow&\dfrac{8x}{3}=8\\\\&\Leftrightarrow&\dfrac{8x}{3}=\dfrac{8}{1}\\\\&\Leftrightarrow&1\times(8x)=3\times 8\\\\&\Leftrightarrow&8x=24\\\\&\Leftrightarrow&x=\dfrac{24}{8}\\\\&\Leftrightarrow&x=3\end{array}$
Comme $3\in\mathbb{Q}$ alors,
$$\boxed{S=\left\lbrace 3\right\rbrace}$$
Exercice 21
Ngor et Diégane ont ensemble $48$ billes, soit $x$ le nombre de billes de Ngor
1) Exprimons en fonction de $x$, le nombre de billes de Diégane.
Soit $x$ le nombre de billes de Ngor.
On sait que la somme des nombres de billes de Diégane et de Ngor est égale à $48.$
Ce qui se traduit par l'équation suivante :
$$\text{nombre de billes de Diégane}+x=48$$
On va résoudre cette équation pour trouver le nombre de billes de Diégane.
Il suffit alors de faire passer $x$ de la gauche vers la droite en changeant son signe.
$$\text{nombre de billes de Diégane}+x=48\ \Leftrightarrow\ \text{nombre de billes de Diégane}=48-x$$
Donc, le nombre de billes de Diégane est égal à $(48-x)$
2) Déterminons $x$ sachant que Ngor a $2$ fois plus de billes que Diégane.
On a :
le nombre de billes de Ngor est égal à : $x$
le nombre de billes de Diégane est égal à : $48-x$
Comme Ngor a $2$ fois plus de billes que Diégane alors, cela se traduit par l'équation suivante :
$$x=2(48-x)$$
En résolvant cette équation, on obtient :
$\begin{array}{rcl} x=2(48-x)&\Leftrightarrow&x=2\times 48-2\times x\\ \\&\Leftrightarrow&x=96-2x\\\\&\Leftrightarrow&x+2x=96\\\\&\Leftrightarrow&3x=96\\\\&\Leftrightarrow&x=\dfrac{96}{3}\\\\&\Leftrightarrow&x=32\end{array}$
Par suite, Ngor a $32$ billes et Diégane en a $16.$
Vérification :
On a : $32+16=48$
Ce qui montre que la somme des billes de Ngor et de Diégane est bien égale à $48.$
Exercice 22
Un père a $24$ ans de plus que son fils, calculons l'âge de chacun quand ils auront ensemble $100$ ans.
Soit $x$ l'âge du fils alors.
Comme le père a $24$ ans de plus que son fils alors, l'âge du père sera égal à : $(24+x).$
Le père et son fils auront ensemble $100$ ans. Ce qui peut se traduire sous forme d'équation par :
$$(24+x)+x=100$$
En résolvant cette équation, on obtient :
$\begin{array}{rcl} (24+x)+x=100&\Leftrightarrow&24+x+x=100\\ \\&\Leftrightarrow&2x=100-24\\\\&\Leftrightarrow&2x=76\\\\&\Leftrightarrow&x=\dfrac{76}{2}\\\\&\Leftrightarrow&x=38\end{array}$
Donc, l'âge du fils est de : $38$ ans.
On a : $24+38=62$ donc, le père a $62$ ans.
Vérification :
On a : $62+38=100$
Donc, la somme de leur âge est bien égale à $100$ ans.
Exercice 23
Les dimensions d'un rectangle sont $3\ $ et $\ 4\;m$
Déterminons le nombre qu'il faut ajouter à la longueur et à la largeur pour que le périmètre double.
Le périmètre du rectangle est :
$\begin{array}{rcl} P&=&2\times(3+4)\\\\&=&2\times 7\\\\&=&21\end{array}$
Donc, $P=21\;cm$
Soit $x$ le nombre à ajouter à la longueur et à la largeur alors :
la longueur devient : $(4+x)$
la largeur devient : $(3+x)$
Ainsi, le nouveau périmètre est donné par :
$$2[(4+x)+(3+x)]$$
Ce périmètre double si, et seulement si,
$$2[(4+x)+(3+x)]=2\times 21=42$$
Donc, en résolvant l'équation $2[(4+x)+(3+x)]=42$ on trouve la valeur de $x.$
On a :
$\begin{array}{rcl} 2[(4+x)+(3+x)]=42&\Leftrightarrow&2(4+x+3+x)=42\\\\&\Leftrightarrow&2\times 4+2\times x+2\times 3+2\times x=42\\ \\&\Leftrightarrow&8+2x+6+2x=42\\\\&\Leftrightarrow&4x=42-8-6\\\\&\Leftrightarrow&4x=28\\\\&\Leftrightarrow&x=\dfrac{28}{4}\\\\&\Leftrightarrow&x=7\end{array}$
Ainsi, il faut ajouter $7\;cm$ à la longueur et à la largeur pour que le périmètre double.
Par suite :
la longueur sera donnée par : $4+7=11\;cm$
la largeur sera donnée par : $3+7=10\;cm$
Vérification :
On a : $2\times(11+10)=2\times 21=42$
Ce qui prouve que le périmètre a doublé.
Exercice 24
Une mère a $15$ ans de plus que sa fille, dans $10$ ans l'âge de la mère sera le double de l'âge de la fille ;
Déterminons l'âge de la mère et celui de la fille.
Soit $x$ l'âge de la fille.
Comme la mère a $15$ ans de plus que sa fille alors, l'âge de la mère est : $(x+15)$
Ainsi, dans $10$ ans
la fille aura : $(x+10)$ ans
la mère aura : $[(x+15)+10]$ ans
Comme dans $10$ ans l'âge de la mère sera le double de l'âge de la fille alors, on peut le traduire par l'équation suivante :
$$[(x+15)+10]=2(x+10)$$
En résolvant cette équation, on obtient :
$\begin{array}{rcl} [(x+15)+10]=2(x+10)&\Leftrightarrow&(x+15+10)=2\times x+2\times 10\\\\&\Leftrightarrow&x+25=2x+20\\ \\&\Leftrightarrow&x-2x=20-25\\\\&\Leftrightarrow&-x=-5\\\\&\Leftrightarrow&x=\dfrac{-5}{-1}\\\\&\Leftrightarrow&x=5\end{array}$
Donc, la fille a $5$ ans.
On a : $5+15=20$ donc, la mère a $20$ ans
Dans $10$ ans la mère aura $30$ ans et sa fille aura $15$ ans.
Vérification :
On a : $30=2\times 15$
Ce qui confirme que l'âge de la mère est bien le double de celui de sa fille.
Exercice 25
Nafi a eu $13\ $ et $\ 15$ aux $2$ premiers contrôles de Maths.
Déterminons la note qu'elle doit obtenir au $3^{\text{ème}}$ contrôle pour que sa moyenne soit $16$
Soit $x$ la note obtenue au $3^{\text{ème}}$ contrôle.
Donc, pour calculer la moyenne de Nafi, on fait :
$$\dfrac{13+15+x}{3}$$
Pour que cette moyenne soit égale à $16$, on pose l'équation suivante :
$$\dfrac{13+15+x}{3}=16$$
En résolvant cette équation, on obtient :
$\begin{array}{rcl} \dfrac{13+15+x}{3}=16&\Leftrightarrow&\dfrac{28+x}{3}=\dfrac{16}{1}\\\\&\Leftrightarrow&1\times(28+x)=3\times 16\\ \\&\Leftrightarrow&28+x=48\\\\&\Leftrightarrow&x=48-28\\\\&\Leftrightarrow&x=20\end{array}$
Donc, Nafi doit obtenir $20$ au $3^{\text{ème}}$ contrôle pour que sa moyenne soit $16.$
Vérification :
On a : $\dfrac{13+15+20}{3}=\dfrac{48}{3}=16$
Ce qui montre bien que sa moyenne est $16$ lorsque sa note au $3^{\text{ème}}$ contrôle est $20.$
Exercice 26
Un terrain rectangulaire a un périmètre de $4.5\;km$ ; la longueur mesure $350\;m$ de plus que la largeur, déterminons les dimensions du terrain.
Soit $x$ la dimension de la largeur.
Comme la longueur mesure $350\;m$ de plus que la largeur alors, la dimension de la longueur est : $(x+350)$
Donc, le périmètre est donné par :
$$2[(x+350)+x]$$
Or, on sait que ce terrain a un périmètre de $P=4.5\;km.$ En convertissant en mètre, on obtient : $P=4.5\;km=4\,500\;m$
Ainsi, on l'équation suivante :
$$2[(x+350)+x]=4\,500$$
On va résoudre cette équation pour trouver la valeur de $x$ qui représente la dimension de la largeur.
On a :
$\begin{array}{rcl} 2[(x+350)+x]=4\,500&\Leftrightarrow&2(x+350+x)=4\,500\\\\&\Leftrightarrow&2(2x+350)=4\,500\\\\&\Leftrightarrow&2\times 2x+2\times 350+x=4\,500\\ \\&\Leftrightarrow&4x+700=\,500\\\\&\Leftrightarrow&4x=4\,500-700\\\\&\Leftrightarrow&4x=3\,800\\\\&\Leftrightarrow&x=\dfrac{3\,800}{4}\\\\&\Leftrightarrow&x=950\end{array}$
Alors, la largeur mesure $950\;m$
On a : $950+350=1\,300$ donc, la longueur mesure $1\,300\;m$
Vérification :
On a :
$\begin{array}{rcl}\text{Périmètre}&=&2(1\,300+950)\\\\&=&2\times 2\,250\\\\&=&4\,500\;m\\\\&=&4.5\;km\end{array}$
Donc, les dimensions vérifient bien le périmètre de ce terrain.
Exercice 27
Nogaye dépense les trois cinquième de son argent pour acheter un livre.
Elle donne ensuite le quart du reste à sa sœur Ami. Elle se retrouve après avec seulement $12\,000$ francs.
Déterminons la somme d'argent que Nogaye disposait.
Soit $x$ la somme totale que dispose Nogaye.
Comme elle dépense les trois cinquième de son argent pour acheter un livre alors, la dépense pour ce livre est : $\dfrac{3}{5}x$
Ainsi, la somme qui lui reste est : $\left(x-\dfrac{3}{5}x\right)$
Nogaye donne ensuite le quart de ce reste à sa sœur Ami. Donc, la somme donnée à Ami est : $\dfrac{1}{4}\left(x-\dfrac{3}{5}x\right)$
Enfin, la somme qui lui reste est : $12\,000\;F$
Par ailleurs, on sait que la somme dépensée pour le livre, la somme donnée à Ami et la somme restante constituent la somme totale d'argent $x$ que Nogaye disposait.
Ainsi, on peut écrire :
$$\dfrac{3}{5}x+\dfrac{1}{4}\left(x-\dfrac{3}{5}x\right)+12\,000=x$$
En résolvant cette équation, on obtient :
$\begin{array}{rcl} \dfrac{3}{5}x+\dfrac{1}{4}\left(x-\dfrac{3}{5}x\right)+12\,000=x&\Leftrightarrow&\dfrac{3}{5}x+\dfrac{1}{4}x-\dfrac{1}{4}\times\dfrac{3}{5}x+12\,000=x\\\\&\Leftrightarrow&\dfrac{3}{5}x+\dfrac{1}{4}x-\dfrac{3}{20}x-x=-12\,000\\\\&\Leftrightarrow&\dfrac{12}{20}x+\dfrac{5}{20}x-\dfrac{3}{20}x-\dfrac{20}{20}x=-12\,000\\ \\&\Leftrightarrow&-\dfrac{6}{20}x=-12\,000\\\\&\Leftrightarrow&x=\dfrac{-12\,000}{-\dfrac{6}{20}}\\\\&\Leftrightarrow&x=-12\,000\times\left(-\dfrac{20}{6}\right)\\\\&\Leftrightarrow&x=\dfrac{12\,000\times 20}{6}\\\\&\Leftrightarrow&x=\dfrac{240\,000}{6}\\\\&\Leftrightarrow&x=40\,000\end{array}$
Donc, Nogaye disposait de $40\,000\;F$
On a :
$\begin{array}{rcl}\dfrac{3}{5}\times 40\,000&=&\dfrac{3\times 40\,000}{5}\\\\&=&\dfrac{120\,000}{5}\\\\&=&24\,000\end{array}$
Ainsi, Nogaye a dépensé $24\,000\;F$ pour acheter un livre.
Aussi,
$\begin{array}{rcl}\dfrac{1}{4}\left(40\,000-\dfrac{3}{5}\times 40\,000\right)&=&\dfrac{1}{4}\left(40\,000-\dfrac{3\times 40\,000}{5}\right)\\\\&=&\dfrac{1}{4}\left(40\,000-\dfrac{120\,000}{5}\right)\\\\&=&\dfrac{1}{4}\left(40\,000-24\,000\right)\\\\&=&\dfrac{1}{4}\times 16\,000\\\\&=&\dfrac{16\,000}{4}\\\\&=&4\,000\end{array}$
Donc, Nogaye a donné $4\,000\;F$ à sa sœur Ami
Vérification :
On a : $24\,000+4\,000+12\,000=40\,000$
Exercice 28
1) Déterminons le nombre de places réservées aux passagers
Soit $x$ le nombre de places réservées aux passagers.
$-\ $ A l'embarquement à Dakar, les $\dfrac{3}{4}$ des sièges sont occupées.
Donc, le nombre de places occupés à l'embarquement à Dakar est de :
$$\dfrac{3}{4}x$$
$-\ $ A l'escale de Bamako, $45$ passagers descendent et $27$ montent.
Ce qui veut dire que le nombre de places occupées au départ de Bamako est de :
$$\boxed{\dfrac{3}{4}x-45+27}\qquad(1)$$
On sait par ailleurs, que l'avion est plein aux $\dfrac{2}{3}.$
Donc, le nombre de places occupées au départ de Bamako peut encore s'exprimer par :
$$\boxed{\dfrac{2}{3}x}\qquad(2)$$
Par suite, l'égalité des relations (1) et (2) donne :
$$\boxed{\dfrac{3}{4}x-45+27=\dfrac{2}{3}x}$$
En résolvant cette dernière équation, on trouvera le nombre $x$, de places réservées aux passagers.
On a :
$\begin{array}{rcl} \dfrac{3}{4}x-45+27=\dfrac{2}{3}x&\Leftrightarrow&\dfrac{3}{4}x-\dfrac{2}{3}x=45-27\\ \\&\Leftrightarrow&\dfrac{9}{12}x-\dfrac{8}{12}x=18\\ \\&\Leftrightarrow&\dfrac{x}{12}=18\\ \\&\Leftrightarrow&x=18\times 12\\ \\&\Leftrightarrow&x=216\end{array}$
D'où, $\boxed{x=216}$
Ainsi, cet avion compte $216$ places réservées aux passagers.
2) Déterminons le nombre de passagers débarquant à Abidjan.
Soit $A$ le nombre de passagers débarquant à Abidjan et $B$ le nombre de passagers au départ de Bamako.
$-\ $ Comme au départ de Bamako l'avion était plein aux $\dfrac{2}{3}$ alors, on a :
$$B=\dfrac{2}{3}x=\dfrac{2}{3}\times 216=144$$
$-\ $ A l'escale de Ouaga, la moitié de ces $144$ passagers descend et $25$ montent.
Cela se traduit par :
$$144-\dfrac{144}{2}+25=144-72+25=97$$
Donc, au départ de Ouaga, l'avion compte $97$ passagers à destination d'Abidjan.
Ainsi, le nombre de passagers débarquant à Abidjan est :
$$\boxed{A=97}$$
Auteur:
Diny Faye

Commentaires
Anonyme (non vérifié)
mar, 02/25/2020 - 00:15
Permalien
Correction de l'exercice 28
Anonyme (non vérifié)
lun, 11/30/2020 - 22:17
Permalien
Correction exercice 24
Anonyme (non vérifié)
sam, 05/23/2020 - 16:04
Permalien
Je pense vraiment que les
Anonyme (non vérifié)
dim, 02/28/2021 - 23:03
Permalien
Mien mais Les corrections sur
Anonyme (non vérifié)
sam, 06/26/2021 - 21:04
Permalien
Please la correction des
Mor Cisse (non vérifié)
sam, 03/13/2021 - 21:09
Permalien
Exercice intéressants mais y
Maimouna kane (non vérifié)
ven, 04/09/2021 - 18:12
Permalien
C'est bien mais les
Lena Ndour (non vérifié)
jeu, 05/27/2021 - 05:25
Permalien
Mais l'exercice 6
DJEVI (non vérifié)
sam, 06/03/2023 - 18:01
Permalien
COMMENTAIRE SUR EXERCICE NUM2RO 21
DJEVI (non vérifié)
sam, 06/03/2023 - 18:01
Permalien
COMMENTAIRE SUR EXERCICE NUM2RO 21
Ajouter un commentaire