Solution des exercices : Principes des actions réciproques - 3e

Classe:

Troisième

Exercice 1

L'action et la réaction sont des actions réciproques qui se produisent simultanément : on les appelle des forces d'interactions. Elles agissent sur deux objets différents et produisent alors un mouvement. Ce sont des forces directement opposées : elles ont même intensité, même direction et des sens opposées. Quand deux objets interagissent, l'action de l'un est toujours égale à la réaction de l'autre : ce sont des forces directement opposées.

Exercice 2

Deux forces peuvent être opposées ou directement opposées :

1) Caractéristiques des forces opposées :

$-\ $ points d'application différents

$-\ $ même droite d'action

$-\ $ sens différents

$-\ $ intensités différentes

Caractéristiques des forces directement opposées :

$-\ $ points d'application différents

$-\ $ même droite d'action

$-\ $ sens différents

$-\ $ même intensité

2) Exemple de forces opposées : le recul des armes à feu

Exemple de forces directement opposées : la propulsion par réaction des avions et des fusées

Activités

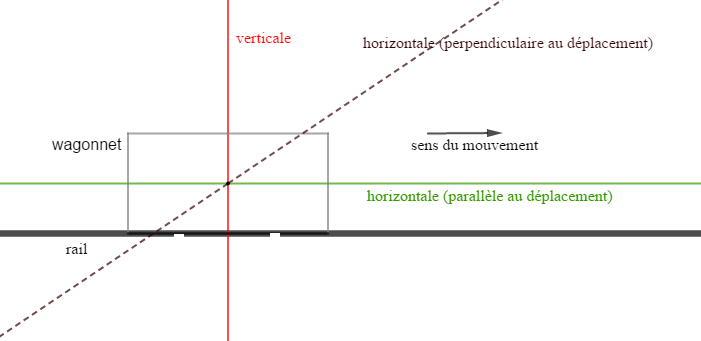
Un wagonnet lancé, se déplace sans frottement sur un rail horizontal.

On exerce sur lui une force $F$ par l'intermédiaire d'un souffleur d'air.

Pour modifier sa vitesse, plusieurs directions sont envisagées.

1) La direction "la plus efficace" pour modifier la vitesse du wagonnet est l'horizontale (parallèle au déplacement).

2) Les directions qui ne modifient pas la vitesse du wagonnet sont : la verticale, l'horizontale (perpendiculaire au déplacement).

3) Représentons les différentes directions envisagées

4) L'expression de $W$ pour la direction la plus efficace pour augmenter la vitesse est donnée par :

$$W=F\times d$$

où $d$ est la distance parcourue ou déplacement.

5) La force $F$ exercée par le souffleur favorise le déplacement du wagonnet si cette force est de même sens que le déplacement.

Le travail est alors moteur.

6) La force $F$ exercée par le souffleur s'oppose au déplacement du wagonnet lorsqu'elle est de sens contraire au sens de déplacement du wagonnet.

Par conséquent, le travail est résistant.

Exercice 3 Maitrise de connaissances

Recopions et complétons les phrases suivantes par les mots :

durée, joule, intensité, watt, moteur, longueur, travail, résistant, déplacement.

Le travail d'une force constante colinéaire au déplacement est égal au produit de l'intensité de la force par la longueur du déplacement de son point d'application.

Dans le système international, le joule est l'unité de travail.

Un travail est dit résistant si la force et le déplacement sont de sens contraire.

La puissance moyenne d'une force est le quotient du travail par la durée mise à l'effectuer.

Le watt est l'unité de puissance dans le système international

Exercice 4 Ordres de grandeurs

Dans le tableau ci-dessous, associons chaque système à l'ordre de grandeur de sa puissance mécanique :

$$\begin{array}{|l|c|} \hline \text{Système}&\text{Ordre de grandeur}\\ \hline \text{Moteur d'automobile}&2\;kW\\ \hline \text{Réacteur d'avion}&25\;MW\\ \hline \text{Moteur de camion}&200\;kW\\ \hline \text{Homme travaillant physiquement}&150\;W\\ \hline \text{Moteur de montre}&10^{-6}\;W\\ \hline \end{array}$$

Exercice 5 Déménageur

Un déménageur pousse une armoire sur un sol horizontal.

Il exerce une force $F$ constante, horizontale, parallèle au déplacement rectiligne, de valeur $100\;N.$

Les frottements sont assimilables à une force constante $(f)$ opposée au déplacement et d'intensité $10\;N.$

1) Calculons le travail $W_{_{(F)}}$ de la force pour un déplacement de $150\;cm$ de son point d'application.

On a : $W_{_{(F)}}=F\times d\ $ où $d$ est le déplacement égal à $150\;cm=150.10^{-2}\;m$

A.N : $W_{(F)}=100\times 150.10^{-2}=150$

Ainsi, $\boxed{W_{_{(F)}}=150\;J}$

2) Calculons le travail $W_{_{(f)}}$ de la force de frottement :

Soit : $W_{_{(f)}}=-f\times d$

Alors : $W_{_{(f)}}=-10\times150.10^{-2}$

D'où, $\boxed{W_{_{(f)}}=-15\;J}$

Nature du travail : résistant

Exercice 6 Travail du poids

L'intensité de la pesanteur est $g=9.8\;N.kg^{-1}$

Une balle de tennis de masse $m=60\;g$ tombe d'une hauteur $h=1.5\;m.$

Calculons le travail $W_{_{(P)}}$ du poids $P$ :

Soit : $W_{_{(P)}}=P\times h$

Or, $P=m\times g$ donc, $W_{_{(P)}}=m\times g\times h$

A.N : $W_{_{(P)}}=60.10^{-3}\times 9.8\times 1.5=0.882$

Ainsi, $\boxed{W_{_{(P)}}=0.882\;J}$

Par conséquent, le travail est moteur.

Exercice 7 Puissance moyenne et vitesse

Un mobile $M$, sous l'action d'une force constante $\vec{F}$ se déplace d'une longueur $L$ pendant une durée $t$ avec une vitesse constante $\vec{v}$ colinéaire à $\vec{F}$ et de même sens.

1) Montrons que la puissance $\mathcal{P}$ se met sous la forme : $\mathcal{P}=F\times v$

On sait que : $\mathcal{P}=\dfrac{W_{_{(F)}}}{t}\ $ avec $W_{_{(F)}}=F\times L$

Alors, $\mathcal{P}=\dfrac{F\times L}{t}=F\times\dfrac{L}{t}\ $ ; or $\dfrac{L}{t}=v$

Donc, en remplaçant $\dfrac{L}{t}$ par $v$, on obtient :

$$\mathcal{P}=F\times v$$

2) Une charge est soulevée à $d=3.1\;m$ du sol en $t=3.2\;s$ avec une force $F$ constante et dirigée suivant la verticale.

La puissance moyenne de cette force est $\mathcal{P}=600\;W.$

Déterminons la valeur de cette force.

On a : $\mathcal{P}=F\times v\ $ et $\ v=\dfrac{d}{t}$

Donc, en remplaçant $v$ par $\dfrac{d}{t}$, on obtient :

$\begin{array}{rcrcl}\mathcal{P}=F\times\dfrac{d}{t}&\Rightarrow&\mathcal{P}&=&\dfrac{F\times d}{t}\\ \\&\Rightarrow&F\times d&=&\mathcal{P}\times t\\ \\&\Rightarrow&F&=&\dfrac{\mathcal{P}\times t}{d}\end{array}$

A.N : $F=\dfrac{600\times 3.2}{3.1}=619.3$

Ainsi, $\boxed{F=619.3\;N}$

Exercice 8 haltérophilie

Une barre de masse $m=150\;kg$ est soulevée par un haltérophile d'une hauteur $h=1.95\;m$ en $t=2s.$ L'intensité de la pesanteur est $g=9.8\;N.kg^{-1}$

Calculons la puissance moyenne $\mathcal{P}$ de la force développée par l'haltérophile.

Soit : $\mathcal{P}=F\times v\ $ où $v$ est la vitesse de déplacement de la barre et $F$ la résultante des forces exercées par l'haltérophile.

Comme $F$ est verticale et que sa valeur est constante et égale au poids de la barre alors, on a : $F=P=m\times g$

De plus, $\ v=\dfrac{h}{t}$

Donc, en remplaçant $F\ $ et $\ v$ respectivement par $m\times g\ $ et $\ \dfrac{h}{t}$, on obtient :

$$\mathcal{P}=m\times g\times\dfrac{h}{t}=\dfrac{m\times g\times h}{t}$$

A.N : $\mathcal{P}=\dfrac{150\times 9.8\times 1.95}{2}=1433.25$

D'où, $\boxed{\mathcal{P}=1433.25\;W}$

Exercice 9 Pompe à eau

Un moteur de pompe remonte l'eau d'un puits.

La profondeur du puits est $L=15\;m$ et le débit est $d=10\;m^{3}.h^{-1}$

1) Calculons le volume d'eau remontée en une heure.

Soit $V_{e}$ le volume d'eau remontée du puits en un temps $t=1\;h.$

Alors, $V_{e}=d\times t$

A.N : $V_{e}=10\times 1=10$

D'où, $\boxed{V_{e}=10\;m^{3}}$

2) Calculons le travail $W_{_{(F)}}$, de la force motrice $F$ en une heure.

On a : $W_{_{(F)}}=F\times L\ $ où $F$ est égale en intensité au poids $P_{e}$ de l'eau pompée.

Donc, en remplaçant $F$ par $P_{e}$, on obtient : $W_{_{(F)}}=P_{e}\times L\ $ or, $P_{e}=m_{e}\times g$

Par suite, $W_{_{(F)}}=m_{e}\times g\times L\ $ avec $m_{e}=\rho_{e}\times V_{e}$

D'où, $W_{_{(F)}}=\rho_{e}\times V_{e}\times g\times L\ $ avec $\rho_{e}=10^{3}kg.m^{-3}\;;\ g=9.8\;N.kg^{-1}$

A.N : $W_{_{(F)}}=10^{3}\times 10\times 9.8\times 15=1470000$

Ainsi, $\boxed{W_{_{(F)}}=1470000\;J=1470\;kJ}$

3) Le travail cette force motrice est moteur.

4) Déterminons la puissance moyenne $\mathcal{P}$, du moteur

Soit : $\mathcal{P}=\dfrac{W_{_{(F)}}}{t}$

A.N : $\mathcal{P}=\dfrac{1470000}{1}$

D'où, $\boxed{\mathcal{P}=1470000\;W=1470\;kW}$

Exercice 10 Principe des actions réciproques

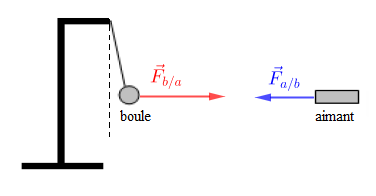
Une boule en fer (a) est accrochée à un pendule par l'intermédiaire d'un fil initialement vertical.

On approche un aimant (b) de la boule (a) qui s'écarte de sa position initiale.

Représentons avec la même échelle

1) La force $\vec{F}_{a/b}$ que la boule (a) exerce sur l'aimant (b):

2) La force $\vec{F}_{b/a}$ que l'aimant (b) exerce sur la boule (a) :

N.B : puisque la boule (a) s'écarte de sa position initiale sous l'effet de la force $\vec{F}_{b/a}$ et que l'aimant reste immobile alors, on peut écrire :

$$\|\vec{F}_{b/a}\|>\|\vec{F}_{a/b}\|$$

Ce qui signifie que la longueur du vecteur $\vec{F}_{b/a}$, représentant la force que l'aimant exerce sur la boule reste supérieure à la longueur du vecteur $\vec{F}_{a/b}$, représentant la force que la boule exerce sur l'aimant.

Auteur:

Aliou ndiaye