Solution des exercices : Droites des milieux - 4e
Classe:
Quatrième
Exercice 1
Soit $ABC$ un triangle isocèle en $A$ tel que :
$$AB=5\;cm\quad\text{et}\quad BC=4\;cm$$
$I\ $ et $\ K$ sont les milieux respectifs de $[AB]\ $ et $\ [AC].$
1) Faisons une figure complète.
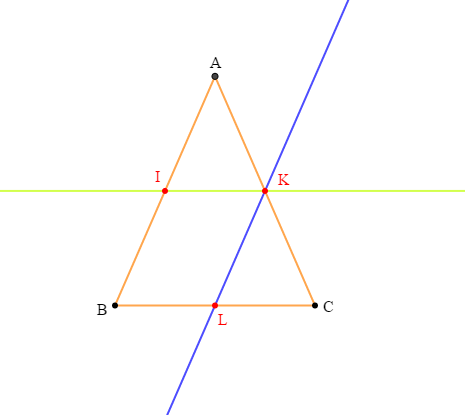
2) a) Montrons que $(IK)\ $ et $\ (BC)$ sont parallèles.
$I\ $ et $\ K$ étant les milieux respectifs de $[AB]\ $ et $\ [AC]$ alors, la droite $(IK)$ passant par $I\ $ et $\ K$ est appelée droite des milieux.
Ainsi, d'après le théorème de la droite des milieux, la droite $(IK)$ est parallèle au troisième côté du triangle $ABC.$
D'où, $(IK)\ $ et $\ (BC)$ sont parallèles.
b) Calculons $IK$ en précisant le théorème utilisé.
Dans un triangle, le segment joignant les milieux de deux côtés a pour longueur la moitié de la longueur du troisième côté.
Ainsi, $IK=\dfrac{BC}{2}=\dfrac{4}{2}=2\;cm$
3) La parallèle à $(AB)$ passant par $K$ coupe $(BC)$ en $L.$
Montrons que $L$ est le milieu de $[BC].$
On a : la droite qui est parallèle à $(AB)$ et qui passe par $K$ milieu de $[AC]$, coupe $(BC)$ en $L.$
Or, d'après la réciproque du théorème de la droite des milieux, on sait que, si une droite est parallèle à un côté et si elle passe par le milieu d'un deuxième côté alors elle passe par le milieu du troisième côté.
Par conséquent, $L$ est milieu de $[BC]$
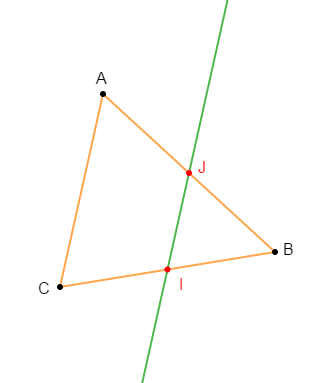
Exercice 2
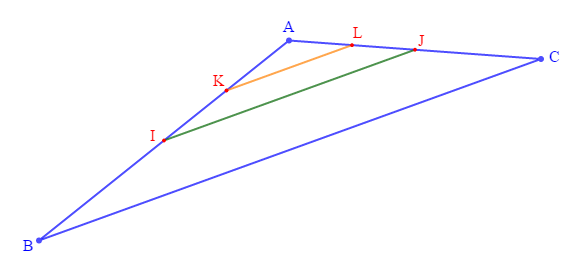
Soit $ABC$ un triangle, $I$ milieu du segment $[AB]\;,\ J$ milieu du segment $[AC]\;,\ K$ milieu du segment $[AI]$ et $L$ milieu du segment $[AJ].$
1) Faisons une figure.

2) Démontrons que : $4KL=BC.$
Dans le triangle $ABC$, on a : $I$ milieu du segment $[AB]\ $ et $\ J$ milieu du segment $[AC].$
Or, dans un triangle, le segment joignant les milieux de deux côtés a pour longueur la moitié de la longueur du troisième côté. Donc,
$$IJ=\dfrac{BC}{2}\qquad(\text{égalité 1})$$
Par ailleurs, en considérant le petit triangle $AIJ$, on a : $K$ milieu du segment $[AI]\ $ et $\ L$ milieu du segment $[AJ].$
Comme dans un triangle, le segment joignant les milieux de deux côtés a pour longueur la moitié de la longueur du troisième côté alors,
$$KL=\dfrac{IJ}{2}\qquad(\text{égalité 2})$$
Or, dans l'égalité 1, on avait $IJ=\dfrac{BC}{2}$ donc, en remplaçant dans l'égalité 2, on obtient :
$$KL=\dfrac{\dfrac{BC}{2}}{2}=\dfrac{BC}{2}\times\dfrac{1}{2}$$
Ce qui donne : $KL=\dfrac{BC}{4}$
D'où, $4KL=BC$
Exercice 3
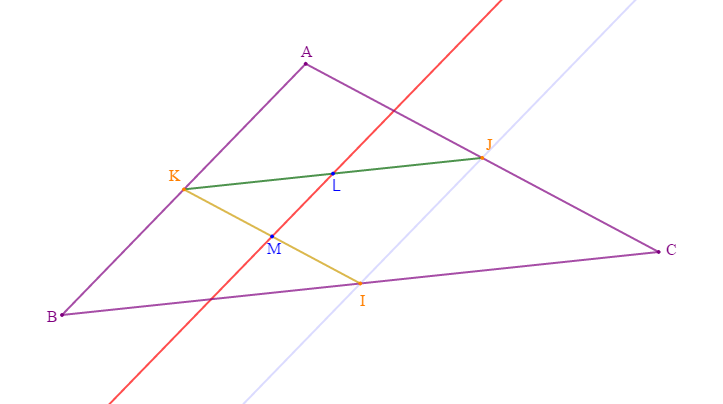
On suppose que $AB=7\;cm\;,\ AC=8\;cm\ $ et $\ BC=12\;cm$ et on désigne par $I\;,\ J\ $ et $\ K$ les milieux respectifs des côtés $[BC]\;,\ [AC]\ $ et $\ [AB].$ On désigne par $L\ $ et $\ M$ les milieux respectifs de $[KJ]\ $ et $\ [KI].$
1) Faisons une figure complète.

2) Prouvons que la droite $(LM)$ est parallèle à la droite $(AB).$
Dans le triangle $IJK$, on a : $L$ milieu de $[KJ]\ $ et $\ M$ milieu de $[KI].$
Ainsi, d'après le théorème de la droite des milieux, la droite $(LM)$, passant par les milieux respectifs de deux côtés, est parallèle au troisième côté du triangle $IJK.$
Par suite, $(LM)$ est parallèle à $(IJ).$
De plus, en considérant le triangle $ABC$, on remarque que la droite $(IJ)$ passe par $J\ $ et $\ I$ ; les milieux respectifs des côtés $[AC]\ $ et $\ [BC]$ du triangle.
Donc, en appliquant le théorème de la droite des milieux, on aura $(IJ)$ parallèle au troisième côté du triangle $ABC.$
D'où, $(IJ)$ est parallèle à $(AB).$
Par ailleurs, on sait que si deux droites sont parallèles alors, toute droite parallèle à l'une est parallèle à l'autre.
Or, $(IJ)$ parallèle à $(AB)$ et $(LM)$ parallèle à $(IJ).$
Par conséquent, $(LM)$ est parallèle à $(AB).$
3) Calculons le périmètre du triangle $KLM.$
Soit $\mathcal{P}_{_{KLM}}$ le périmètre du triangle $KLM.$
On a : $\mathcal{P}_{_{KLM}}=KL+MK+ML$
Comme $L$ es milieu de $[KJ]\ $ et $\ M$ milieu de $[KI]$ alors,
$KL=\dfrac{KJ}{2}\ $ et $\ MK=\dfrac{KI}{2}$
Par suite, $\mathcal{P}_{_{KLM}}=\dfrac{KJ}{2}+\dfrac{KI}{2}+ML$
Par ailleurs, on sait que dans un triangle, le segment joignant les milieux de deux côtés a pour longueur la moitié de la longueur du troisième côté. Donc,
$-\ \ $ Pour le triangle $ABC$, on aura :
$KJ=\dfrac{BC}{2}=\dfrac{12}{2}=6\;cm$
$KI=\dfrac{AC}{2}=\dfrac{8}{2}=4\;cm$
$IJ=\dfrac{AB}{2}=\dfrac{7}{2}=3.5\;cm$
$-\ \ $ Pour le triangle $IJK$, on aura :
$ML=\dfrac{IJ}{2}=\dfrac{3.5}{2}=1.75$
Ainsi, le périmètre $\mathcal{P}_{_{KLM}}$ du triangle $KLM$ sera donné par :
$\begin{array}{rcl}\mathcal{P}_{_{KLM}}&=&\dfrac{KJ}{2}+\dfrac{KI}{2}+ML\\\\&=&\dfrac{6}{2}+\dfrac{4}{2}+1.75\\ \\&=&3+2+1.75\\ \\&=&6.75\end{array}$
D'où, $\boxed{\mathcal{P}_{_{KLM}}=6.75\;cm}$
Remarque : $\mathcal{P}_{_{KLM}}=\dfrac{1}{2}\mathcal{P}_{_{IJK}}=\dfrac{1}{4}\mathcal{P}_{_{ABC}}$
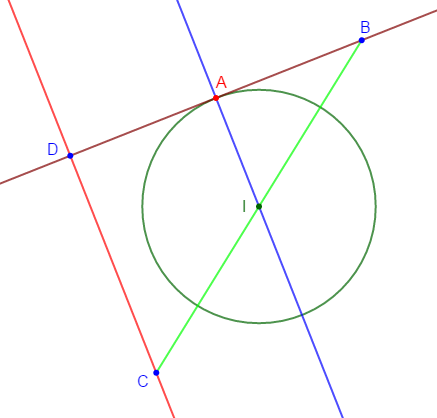
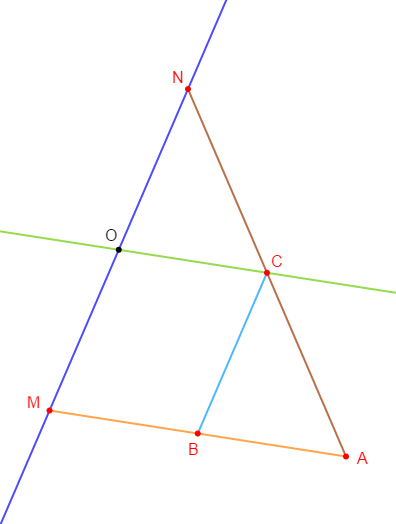
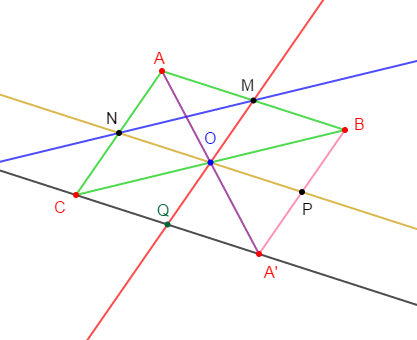
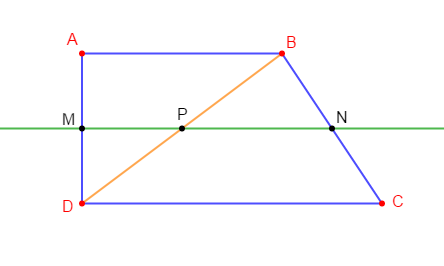
Exercice 4
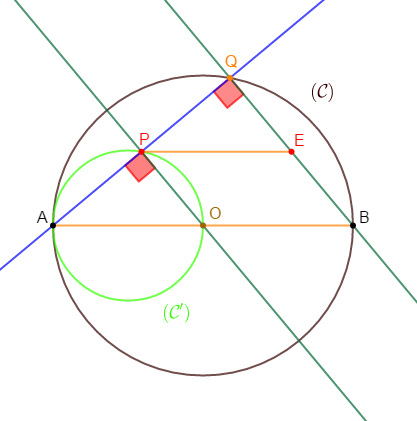
Traçons un cercle $(\mathcal{C})$ de centre $O$ et de diamètre $[AB]\ $ et $\ (\mathcal{C}')$ un cercle de diamètre $[OA].$ Soit $Q$ un point du cercle $(\mathcal{C}).$ La droite $(AQ)$ coupe $(\mathcal{C}')$ en $P.$

1) Démontrons que $P$ est le milieu de $[AQ].$
En effet, on a :
$ABQ$ est un triangle inscrit dans le cercle $(\mathcal{C})$ et dont le côté $[AB]$ est un diamètre de ce cercle. Alors, $ABQ$ est un triangle rectangle en $Q.$
Donc, $(BQ)$ est perpendiculaire à $(AQ).$
De la même manière, $APO$ est un triangle inscrit dans le cercle $(\mathcal{C}')$ et dont le côté $[OA]$ est un diamètre de ce cercle. Alors, $APO$ est un triangle rectangle en $P.$
Par suite, $(OP)$ est perpendiculaire à $(AQ)$ en $P.$
Donc, les droites $(BQ)\ $ et $\ (OP)$ sont perpendiculaires à la même droite $(AQ).$
Or, on sait que si deux droites sont perpendiculaires à une même droite alors, ces deux droites sont parallèles.
D'où, $(BQ)$ est parallèle à $(OP).$
Par suite, $(OP)$ parallèle à $(BQ)$ et passant par le milieu $O$ du côté $[AB]$, coupe $[AQ]$ en $P.$
Or, d'après la réciproque du théorème de la droite des milieux, on sait que : dans un triangle si, une droite est parallèle à un côté et si elle passe par le milieu d'un deuxième côté alors, elle passe par le milieu du troisième côté.
Par conséquent, $P$ est milieu de $[AQ]$
2) Soit $E$ milieu de $[BQ]$, démontrons que : $2PE=AB.$
En effet, d'après une conséquence du théorème de la droite des milieux, on sait que : dans un triangle, le segment joignant les milieux de deux côtés a pour longueur la moitié de la longueur du troisième côté.
Ainsi, dans le triangle $ABQ$, comme $P$ est milieu de $[AQ]\ $ et $\ E$ celui de $[BQ]$ alors, on obtient :
$$PE=\dfrac{AB}{2}$$
Par conséquent, $\boxed{2PE=AB}$
Exercice 5
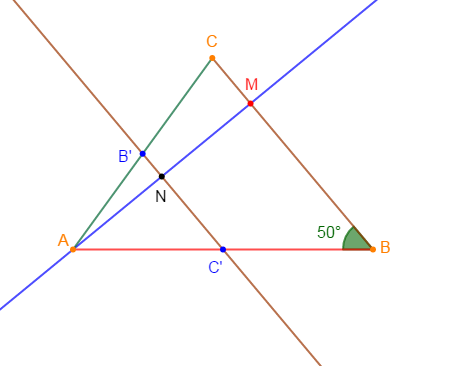
Soit $ABC$ un triangle tel que :
$$AB=6\;cm\;;\ BC=5\;cm\ \text{ et }\ mes\;B=50^{\circ}$$
1) Marquons les points $B'\ $ et $\ C'$ milieux respectifs des segments $[AC]\ $ et $\ [AB].$
2) Soit $M$ un point du segment $[BC]\ $ et $\ (AM)$ coupe $(B'C')$ en $N.$
3) Démontrons que les droites $(BC)\ $ et $\ (B'C')$ sont parallèles puis calculons la distance $B'C'.$
Dans le triangle $ABC$, on a : $B'$ milieu du segment $[AC]\ $ et $\ C'$ celui de $[AB].$
Or, d'après le théorème de la droite des milieux, on sait que : dans un triangle, la droite qui passe par les milieux des deux côtés est parallèle au troisième côté.
Donc, la droite $(B'C')$ passant par $B'\ $ et $\ C'$ est parallèle au troisième côté $[BC]$ du triangle $ABC.$
Par conséquent, les droites $(BC)\ $ et $\ (B'C')$ sont parallèles
Calcul de la distance $B'C'.$
En effet, d'après une conséquence du théorème de la droite des milieux, on sait que : dans un triangle, le segment joignant les milieux de deux côtés a pour longueur la moitié de la longueur du troisième côté.
Ainsi, dans le triangle $ABC$, comme $B'$ est milieu de $[AC]\ $ et $\ C'$ celui de $[AB]$ alors, on obtient :
$$B'C'=\dfrac{BC}{2}$$
Par suite, en remplaçant $BC$ par sa valeur, on trouve :
$$B'C'=\dfrac{5}{2}=2.5$$
D'où, $\boxed{B'C'=2.5\;cm}$
4) Démontrons que $N$ est le milieu de $[AM]$
Considérons le triangle $AMB.$
Alors, d'après la question $3)$ on a : $(B'C')$ parallèle à $(BC)$ ; c'est à dire $(B'C')$ est parallèle à $(AM)$
De plus, la droite $(B'C')$ passant par $C'$ milieu de $[AB]$, coupe $(AM)$ au point $N.$
Or, d'après la réciproque du théorème de la droite des milieux, on sait que : dans un triangle si, une droite est parallèle à un côté et si, elle passe par le milieu d'un deuxième côté alors, elle passe par le milieu du troisième côté.
Par conséquent, $N$ est milieu de $[AM]$
Remarque : on pouvait aussi considérer le triangle $AMC$ et appliquer la même démarche pour démontrer que $N$ est le milieu de $[AM].$

Exercice 6
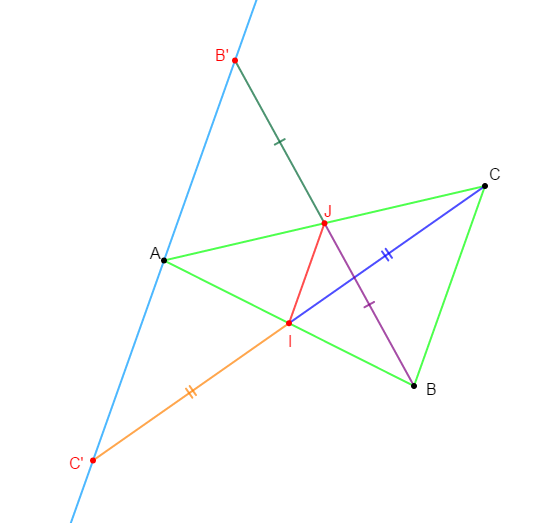
Soit un triangle $ABC$, le point $I$ est le milieu du segment $[AB]$ et le point $J$ est celui du segment $[AC].$
Le point $C'$ est le symétrique de $C$ par rapport à $I$ et le point $B'$ celui de $B$ par rapport à $J.$
1) Faisons une figure complète et codons-la.

2) a) Démontrons que : $(IJ)\parallel(AB')\ $ et $\ IJ=\dfrac{1}{2}AB'.$
En effet, comme $B'$ est le symétrique de $B$ par rapport à $J$ alors, le point $J$ est milieu du segment $[BB'].$
Donc, en considérant le triangle $ABB'$, nous constatons que la droite $(IJ)$ passe par les points $I\ $ et $\ J$ ; milieux respectifs des segments $[AB]\ $ et $\ [BB'].$
Or, d'après le théorème de la droite des milieux, on sait que : dans un triangle, la droite qui passe par les milieux des deux côtés est parallèle au troisième côté.
D'où, $(IJ)$ est parallèle à $(AB')$
Par ailleurs, d'après une conséquence du théorème de la droite des milieux, on sait que : dans un triangle, le segment joignant les milieux de deux côtés a pour longueur la moitié de la longueur du troisième côté.
Donc, en appliquant cette propriété au triangle $ABB'$, on obtient :
$$IJ=\dfrac{1}{2}AB'$$
b) Démontrons que : $(IJ)\parallel(AC')\ $ et $\ IJ=\dfrac{1}{2}AC'.$
En effet, on a : $C'$ symétrique de $C$ par rapport à $I$ donc, $I$ est le milieu du segment $[CC'].$
Alors, dans le triangle $ACC'$, nous remarquons que la droite $(IJ)$ passe par les points $I\ $ et $\ J$ ; milieux respectifs des segments $[CC']\ $ et $\ [AC].$
Or, d'après le théorème de la droite des milieux, on sait que : dans un triangle, la droite qui passe par les milieux des deux côtés est parallèle au troisième côté.
Ainsi, $(IJ)$ est parallèle à $(AC')$
De plus, d'après une conséquence du théorème de la droite des milieux, on sait que : dans un triangle, le segment joignant les milieux de deux côtés a pour longueur la moitié de la longueur du troisième côté.
Donc, en appliquant cette propriété au triangle $ACC'$, on obtient :
$$IJ=\dfrac{1}{2}AC'$$
3) Démontrons que $A$ est le milieu de $[B'C'].$
D'après la question $2)$ on a : $(IJ)\parallel(AB')\ $ et $\ (IJ)\parallel(AC')$
Or, si deux droites sont parallèles, toute droite parallèle à l'une est aussi parallèle à l'autre.
Donc, $(AB')$ est parallèle à $(AC')$
Par suite, les point $C'\;,\ A\ $ et $\ B'$ sont alignés.
Par ailleurs, on a :
$$\left.\begin{array}{rcl} IJ&=&\dfrac{1}{2}AB'\\\\IJ&=&\dfrac{1}{2}AC'\end{array}\right\rbrace\ \Rightarrow\ \dfrac{1}{2}AB'=\dfrac{1}{2}AC'$$
Par suite,
$\begin{array}{rcl} \dfrac{1}{2}AB'=\dfrac{1}{2}AC'&\Leftrightarrow&\dfrac{AB'}{2}=\dfrac{AC'}{2}\\\\&\Leftrightarrow&2\times AB'=2\times AC'\\\\&\Leftrightarrow&AB'=\dfrac{2AC'}{2}\\\\&\Leftrightarrow&AB'=AC'\end{array} $
Donc,
$$AB'=AC'$$
Ainsi, $C'\;,\ A\ $ et $\ B'$ sont trois points alignés tels que $AB'=AC'$
Par conséquent, $A$ est le milieu de $[B'C'].$
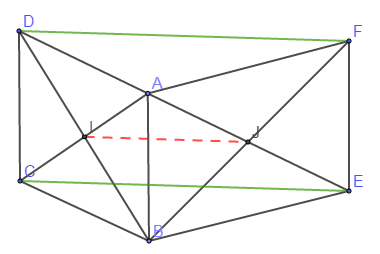
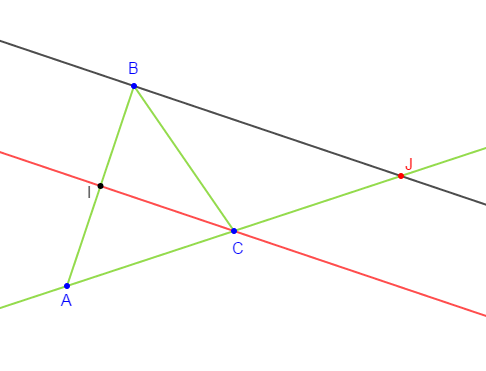
Exercice 7

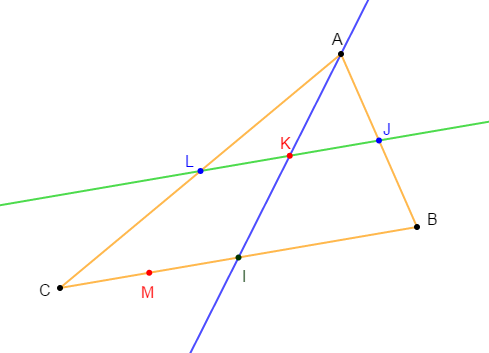
Dans la figure ci-dessus, $ABCD\ $ et $\ ABEF$ sont deux parallélogrammes de centres $I\ $ et $\ J.$
1) Montrer que les droites $(CE)\ $ et $\ (DF)$ sont parallèles (indication : on pourra utiliser $(IJ).$
En effet, comme $ABCD$ est un parallélogramme de centre $I$ alors, ses diagonales $[AC]\ $ et $\ [DB]$ ont même milieu $I.$
Aussi, comme $ABEF$ est un parallélogramme de centre $J$ alors, ses diagonales $[AE]\ $ et $\ [BF]$ ont même milieu $J.$
Donc, en considérant le triangle $DBF$, nous remarquons que la droite $(IJ)$ passe par les points $I\ $ et $\ J$ ; milieux respectifs des segments $[DB]\ $ et $\ [BF].$
Ainsi, d'après le théorème de la droite des milieux, $(IJ)$ est parallèle à $(DF).$
De la même manière, en considérant le triangle $ACE$, nous constatons que la droite $(IJ)$ passe par les points $I\ $ et $\ J$ ; milieux respectifs des segments $[AC]\ $ et $\ [AE].$
Donc, d'après le théorème de la droite des milieux, $(IJ)$ est parallèle à $(CE).$
Ainsi, on a :
$$(IJ)\parallel(DE)\ \text{ et }\ (CE)\parallel(IJ)$$
Or, on sait que : si deux droites sont parallèles, toute droite parallèle à l'une est aussi parallèle à l'autre.
Par conséquent, $(CE)\ $ et $\ (DF)$ sont parallèles.
2) En déduisons la nature du quadrilatère $DFEC.$
En effet, on a :
$ABCD$ parallélogramme alors, $(AB)\ $ et $\ (FE)$ sont parallèles.
$ABEF$ parallélogramme donc, $(AB)\ $ et $\ (DC)$ sont parallèles.
Or, si deux droites sont parallèles, toute droite parallèle à l'une est aussi parallèle à l'autre.
Donc, $(FE)\ $ et $\ (DC)$ sont parallèles.
Par ailleurs, d'après le résultat $1)$, on a : $(CE)\parallel(DF)$
Par suite, le quadrilatère $DFEC$ a ses côtés parallèles $2\ $ à $\ 2.$
Par conséquent, $DFEC$ est un parallélogramme.
Exercice 8
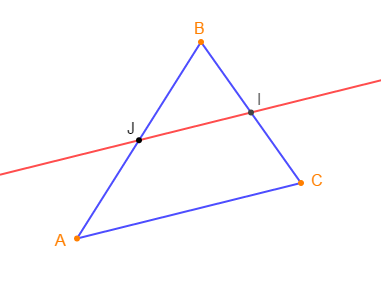
$ABC$ est un triangle, $I$ milieu de $[BC]\;,\ J$ celui de $[AB].$
Démontrons que $(IJ)\ $ et $\ (AC)$ sont parallèles en énonçant la propriété utilisée.
En effet, d'après le théorème de la droite des milieux, on sait que : dans un triangle, la droite qui passe par les milieux des deux côtés est parallèle au troisième côté.
Donc, la droite $(IJ)$ passant par $I\ $ et $\ J$ est parallèle au troisième côté $[AC]$ du triangle $ABC.$
Par conséquent, les droites $(IJ)\ $ et $\ (AC)$ sont parallèles

Exercice 9
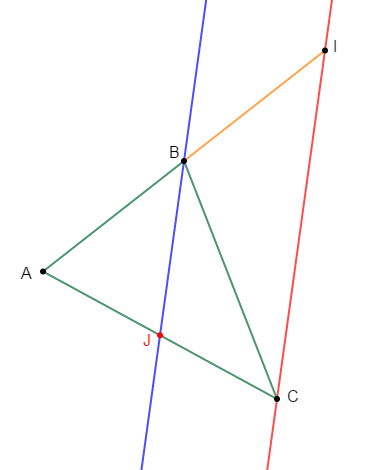
$ABC$ est un triangle, $I$ le symétrique de $A$ par rapport à $B\ $ et $\ J$ milieu de $[AC].$
Démontrons que les droites $(BJ)\ $ et $\ (IC)$ sont parallèles en énonçant la propriété utilisée.
Comme $I$ est le symétrique de $A$ par rapport à $B$ alors, le point $B$ est le milieu du segment $[AI].$
Donc, en considérant le triangle $ACI$, on remarque que la droite $(BJ)$ passe par les points $B\ $ et $\ J$ ; milieux respectifs des segments $[AI]\ $ et $\ [AC].$
Or, d'après le théorème de la droite des milieux, on sait que : dans un triangle, la droite qui passe par les milieux des deux côtés est parallèle au troisième côté.
Par conséquent, les droites $(BJ)\ $ et $\ (IC)$ sont parallèles

Exercice 10
$ABC$ est un triangle, $I$ milieu de $[BC]\;,\ J$ un point de $[AB]$ tel que $(IJ)$ parallèle à $(CA).$
Démontrons que $J$ est le milieu de $[AB]$ en énonçant le théorème utilisé.
En effet, d'après la réciproque du théorème de la droite des milieux, on sait que : dans un triangle si, une droite est parallèle à un côté et si, elle passe par le milieu d'un deuxième côté alors, elle passe par le milieu du troisième côté.
Or, la droite $(IJ)$ passant par $I$ milieu de $[BC]$ et parallèle à $(CA)$, coupe $(AB)$ au point $J.$
Donc, $J$ est le milieu de $[AB]$

Exercice 11
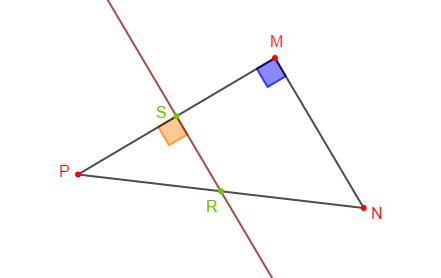
$MNP$ est un triangle rectangle en $M\;,\ S$ milieu de $[MP]$, la perpendiculaire à $(MP)$ en $S$ coupe $[NP]$ en $R.$
Démontrons que $R$ est le milieu de $[NP]$
En effet, $MNP$ étant un triangle rectangle en $M$ alors, $(MN)$ est perpendiculaire à $(MP).$
De plus, $(SR)$ est perpendiculaire à $(MP).$
Or, on sait que si, deux droites sont perpendiculaires à une même droite alors, ces deux droites sont parallèles.
Donc, les droites $(SR)\ $ et $\ (MN)$ sont parallèles.
Par ailleurs, d'après la réciproque du théorème de la droite des milieux, on sait que : dans un triangle si, une droite est parallèle à un côté et si, elle passe par le milieu d'un deuxième côté alors, elle passe par le milieu du troisième côté.
Donc, la parallèle à $(MN)$ passant par $S$ milieu de $[MP]$ coupe $[NP]$ en son milieu.
D'où, $R$ est le milieu de $[NP]$

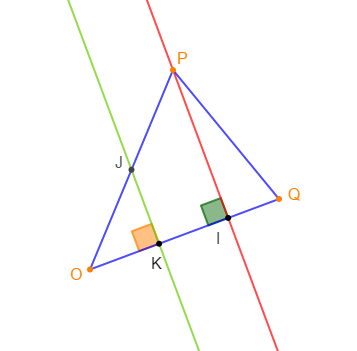
Exercice 12
$OPQ$ est un triangle, $I$ le pied de la hauteur issue de $P.$
$J$ est le milieu de $[OP].$
La perpendiculaire à $(OQ)$ passant par $J$ coupe $[OQ]$ en $K.$
Démontrons que $K$ est le milieu de $[OI].$
En effet, $I$ étant le pied de la hauteur issue de $P$ alors, $(IP)$ est perpendiculaire à $(OQ).$
De plus, $(JK)$ est perpendiculaire à $(OQ).$
Or, on sait que si, deux droites sont perpendiculaires à une même droite alors, ces deux droites sont parallèles.
Donc, les droites $(JK)\ $ et $\ (IP)$ sont parallèles.
Alors, en considérant le triangle $OPI$, on constate que la droite $(JK)$ passant par le milieu de $[OP]$ et parallèle à $(IP)$, coupe $[OI]$ en $K.$
Ainsi, d'après la réciproque du théorème de la droite des milieux, $K$ est le milieu de $[OI].$

Exercice 13
$ABC$ est un triangle, $I$ milieu de $[AB].$
La parallèle à $(IC)$ passant par $B$ coupe $(AC)$ en $J.$
Montrons que $C$ est le milieu de $[AJ]$
En effet, d'après la réciproque du théorème de la droite des milieux, on sait que : dans un triangle si, une droite est parallèle à un côté et si, elle passe par le milieu d'un deuxième côté alors, elle passe par le milieu du troisième côté.
Considérons le triangle $ABJ.$
Alors, on a : $I$ milieu de $[AB]$ et la droite $(IC)$ passant par $I$ et parallèle à $(BJ)$ coupe $[AJ]$ en $C.$
Par conséquent, $C$ est le milieu de $[AJ]$

Exercice 14
1) $ABC$ est un triangle tel que $AB=34\;,\ BC=53\ $ et $\ AC=29.$
$E$ est milieu de $[AB]\ $ et $\ F$ celui de $[BC].$
Alors :
b) $EF=14.5$
En effet, d'après une conséquence du théorème de la droite des milieux, on sait que : dans un triangle, le segment joignant les milieux de deux côtés a pour longueur la moitié de la longueur du troisième côté.
Donc, $EF=\dfrac{AC}{2}=\dfrac{29}{2}=14.5$
D'où, $EF=14.5$
2) $BAC$ est un triangle tel que $AB=6\;,\ AC=7\;,\ BC=8.$
$O\;,\ P\ $ et $\ L$ sont les milieux respectifs des segments $[BA]\;,\ [BC]\ $ et $\ [AC].$
Le périmètre du triangle $POL$ est égal à :
d) $10.5$
En effet, on sait que dans un triangle, le segment joignant les milieux de deux côtés a pour longueur la moitié de la longueur du troisième côté.
Ainsi, chaque côté du triangle $POL$ a pour longueur la moitié de la longueur du côté parallèle du triangle $BAC.$
Par conséquent,
$$\text{périmètre du triangle }POL=\dfrac{\text{périmètre du triangle }BAC}{2}$$
Or,
$\begin{array}{rcl} \text{périmètre du triangle }BAC&=&AB+AC+BC\\\\&=&6+7+8\\\\&=&21\;cm \end{array}$
Donc, $\text{périmètre du triangle }POL=\dfrac{21}{2}=10.5$
D'où, le périmètre du triangle $POL$ est égal à $10.5\;cm$
Exercice 15
Traçons un cercle de centre $I.$
Soit $A$ un point sur ce cercle et $B$ est un point extérieur à ce cercle tels que $(AB)$ soit tangente au cercle.
Soit $C$ le symétrique de $B$ par rapport à $I$ et soit $D$ le symétrique de $B$ par rapport à $A.$
1) Faisons une figure et traçons les droites $(DC)\ $ et $\ (AI).$

2) Démontrons que les droites $(DC)\ $ et $\ (AI)$ sont parallèles.
Considérons le triangle $BCD.$
Comme $C$ est symétrique de $B$ par rapport à $I$ alors, le point $I$ est le milieu de $[BC].$
De même, comme $D$ est le symétrique de $B$ par rapport à $A$ alors, $A$ est milieu de $[BD].$
Ainsi, la droite $(AI)$ passe par les milieux respectifs des côtés $[BD]\ $ et $\ [BC]$ du triangle $BCD.$
Donc, d'après le théorème de la droite des milieux, $(AI)$ est parallèle à $(DC).$
3) Démontrons que $AI=\dfrac{1}{2}DC.$
En effet, d'après une conséquence du théorème de la droite des milieux, on sait que : dans un triangle, le segment joignant les milieux de deux côtés a pour longueur la moitié de la longueur du troisième côté.
Donc, en appliquant cette propriété au triangle $BCD$, on obtient :
$$AI=\dfrac{1}{2}DC$$
Exercice 16
$ABC$ est un triangle tel que $BC=3.5\;cm\;;\ AB=3\;cm\ $ et $\ AC=4\;cm.$
Soit $M$ le point symétrique de $A$ par rapport à $B\ $ et $\ N$ celui de $A$ par rapport à $C.$
1) Démontrons que $(MN)$ est parallèle à $(BC).$
Considérons le triangle $AMN.$
On a : $M$ symétrique de $A$ par rapport à $B$ donc, le point $B$ est le milieu de $[AM].$
De même, $N$ est le symétrique de $A$ par rapport à $C$ donc, $C$ est milieu de $[AN].$
Par suite, la droite $(BC)$ passe donc par $B\ $ et $\ C$ ; milieux respectifs des côtés $[AM]\ $ et $\ [AN]$ du triangle $AMN.$
Ainsi, en appliquant le théorème de la droite des milieux, on obtient :
$$(BC)\parallel(MN)$$
2) Calculons $MN.$
En effet, d'après une conséquence du théorème de la droite des milieux, on sait que : dans un triangle, le segment joignant les milieux de deux côtés a pour longueur la moitié de la longueur du troisième côté.
Donc, en appliquant cette propriété au triangle $AMN$, on obtient :
$$BC=\dfrac{MN}{2}$$
Par conséquent, $MN=2BC=2\times 3.5=7$
D'où, $\boxed{MN=7\;cm}$
3) La parallèle à $(AM)$ passant par $C$ coupe $[MN]$ en $O.$
a) Montrons que $O$ est le milieu de $[MN].$
En effet, d'après la réciproque du théorème de la droite des milieux, on sait que : dans un triangle si, une droite est parallèle à un côté et si, elle passe par le milieu d'un deuxième côté alors, elle passe par le milieu du troisième côté.
Or, dans le triangle $AMN$, on a : $C$ milieu de $[AN]$ et la droite $(OC)$ passant par $C$ et parallèle à $(AM)$, coupe $[MN]$ en $O.$
Par conséquent, $O$ est le milieu de $[MN]$
b) Calculons $OC.$
Comme dans un triangle, le segment joignant les milieux de deux côtés a pour longueur la moitié de la longueur du troisième côté alors, on a :
$$OC=\dfrac{AM}{2}$$
Mais, on sait que $AM=2AB$ car, le point $B$ est milieu du segment $[AM].$
Donc, en remplaçant $AM$ par $2AB$, on obtient :
$\begin{array}{rcl} OC&=&\dfrac{AM}{2}\\\\&=&\dfrac{2AB}{2}\\\\&=&AB\\\\&=&3\end{array}$
D'où, $\boxed{OC=3\;cm}$

Exercice 17
$ABC$ est un triangle ; $M$ milieu de $[AB]\ $ et $\ N$ milieu de $[AC].$
1) Démontrons que les droites $(MN)\ $ et $\ (BC)$ sont parallèles.
En effet, en considérant le triangle $ABC$, nous constatons que la droite $(MN)$ $(BC)$ passe par $M\ $ et $\ N$ ; milieux respectifs des côtés $[AB]\ $ et $\ [AC].$
Or, d'après le théorème de la droite des milieux, on sait que : dans un triangle, la droite qui passe par les milieux des deux côtés est parallèle au troisième côté.
Par conséquent, les droites $(MN)\ $ et $\ (BC)$ sont parallèles.
2) Construisons $A'$, symétrique de $A$ par rapport à $O$, milieu du segment $[BC].$
3) La droite $(ON)$ est parallèle à la droite $(AB)$
Justification :
Comme $N$ est milieu de $[AC]\ $ et $\ O$ celui de $[BC]$ alors, en appliquant le théorème de la droite des milieux sur le triangle $ABC$, on a : $(ON)$ parallèle à $(AB).$
4) Soit $P$ est le milieu de $[BA'].$
Alors, les droites $(OP)\ $ et $\ (AB)$ sont parallèles.
En effet, $A'$ est le symétrique de $A$ par rapport à $O$ donc, le point $O$ est milieu de $[AA'].$
Ainsi, dans le triangle $ABA'$, nous remarquons que la droite $(OP)$ passe par $O\ $ et $\ P$ ; milieux respectifs des côtés $[AA']\ $ et $\ [BA'].$
Donc, en appliquant le théorème de la droite des milieux sur le triangle $ABA'$, on obtient : $(OP)$ parallèle à $(AB).$
5) La parallèle à $(AC)$ passant par $O$ coupe $(CA')$ en $Q.$
Montrons que $Q$ est le milieu de $[CA']$ et que les points $M\;,\ O\ $ et $\ Q$ sont alignés.
Considérons le triangle $ACA'.$
Alors, on a : $O$ milieu de $[AA']$ et la droite $(OQ)$ passant par $O$ et parallèle à la droite $(AC)$, coupe $[CA']$ en $Q.$
Or, d'après la réciproque du théorème de la droite des milieux, on sait que : dans un triangle si, une droite est parallèle à un côté et si, elle passe par le milieu d'un deuxième côté alors, elle passe par le milieu du troisième côté.
Par conséquent, $Q$ est le milieu de $[CA']$
Montrons les points $M\;,\ O\ $ et $\ Q$ sont alignés.
On sait que $(OQ)$ est parallèle à $(AC).$
De plus, en appliquant le théorème de la droite des milieux sur le triangle $ABC$, on a : $(OM)$ parallèle à $(AC).$
Or, on sait que si deux droites sont parallèles, toute droite parallèle à l'une est aussi parallèle à l'autre.
Donc, $(OM)$ est parallèle à $(OQ)$
Par conséquent, les point $M\;,\ O\ $ et $\ Q$ sont alignés.

Exercice 18
$ABCD$ est un trapèze tel que $(AB)$ parallèle à $(DC).$
Soit $M$ le milieu de $[AD]$ et $P$ celui de $[BD]$
1) Démontrons que $(MP)$ est parallèle à $(AB).$
Dans le triangle $ABD$, nous constatons que la droite $(MP)$ passe par $M\ $ et $\ P$ ; milieux respectifs des côtés $[AD]\ $ et $\ [BD].$
Or, d'après le théorème de la droite des milieux, on sait que : dans un triangle, la droite qui passe par les milieux des deux côtés est parallèle au troisième côté.
Donc, en appliquant le théorème de la droite des milieux sur le triangle $ABD$, on obtient : $(MP)$ parallèle à $(AB).$
2) La droite $(MP)$ coupe la droite $(BC)$ en $N.$
Prouvons que $N$ est le milieu de $[BC].$
Considérons le triangle $BCD.$
On sait que $(MP)$ est parallèle à $(AB).$
Or, $(AB)$ est parallèle à $(DC)$ donc, $(MP)$ est parallèle à $(DC).$
Alors, on a : $P$ milieu de $[BD]$ et la droite $(MP)$ passant par $P$ et parallèle à la droite $(DC)$, coupe $[BC]$ en $Q.$
Or, d'après la réciproque du théorème de la droite des milieux, on sait que : dans un triangle si, une droite est parallèle à un côté et si, elle passe par le milieu d'un deuxième côté alors, elle passe par le milieu du troisième côté.
Par conséquent, $N$ est le milieu de $[BC]$
3) Prouvons que $MN=\dfrac{AB+DC}{2}.$
En effet, d'après une conséquence du théorème de la droite des milieux, on sait que : dans un triangle, le segment joignant les milieux de deux côtés a pour longueur la moitié de la longueur du troisième côté.
Donc,
en appliquant cette propriété sur le triangle $ABD$, on obtient :
$$MP=\dfrac{AB}{2}$$
en appliquant cette propriété sur le triangle $BCD$, on obtient :
$$PN=\dfrac{DC}{2}$$
Par ailleurs, $MN=MP+PN$ car, $P\in[MN]$
Donc, en remplaçant $MP\ $ et $\ PN$ par leur expression, on obtient :
$\begin{array}{rcl} MN&=&MP+PN\\\\&=&\dfrac{AB}{2}+\dfrac{DC}{2}\\\\&=&\dfrac{AB+DC}{2}\end{array}$
D'où, $\boxed{MN=\dfrac{AB+DC}{2}}$

Exercice 19
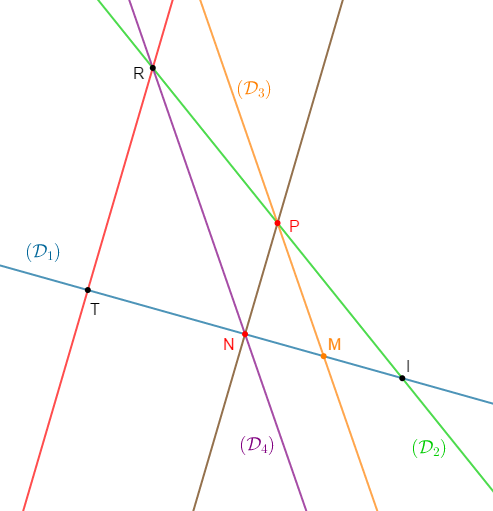
Soit deux droites $(\mathcal{D}_{1})\ $ et $\ (\mathcal{D}_{2})$ sécantes en un point $I.$
Soit $M$ un point appartenant à $(\mathcal{D}_{1})$ et soit $N$ le symétrique de $I$ par rapport à $M.$
Soit $(\mathcal{D}_{3})$ une droite passant par $M$ qui coupe $(\mathcal{D}_{2})$ en $P.$
Soit $(\mathcal{D}_{4})$ la parallèle à $(\mathcal{D}_{3})$ passant par $N$ qui coupe $(\mathcal{D}_{2})$ en $R.$
1) Faisons une figure et traçons la droite $(NP)$ puis la parallèle à la droite $(NP)$ passant par $R\ :$ cette parallèle coupe $(\mathcal{D}_{1})$ en $T.$

2) En considérant le triangle $INR$, démontrons que $P$ est le milieu de $[IR].$
Considérons le triangle $INR.$
On a : $(\mathcal{D}_{4})$ parallèle à $(\mathcal{D}_{3})$ ; ce qui signifie que $(NR)$ est parallèle à $(MP).$
De plus, comme $N$ est le symétrique de $I$ par rapport à $M$ alors, le point $M$ est milieu de $[IN].$
Ainsi, on a : $M$ milieu de $[IN]$ et la droite $(MP)$ passant par $M$ et parallèle à la droite $(NR)$, coupe $[IR]$ en $P.$
Donc, d'après la réciproque du théorème de la droite des milieux, $P$ est milieu de $[IR].$
3) Déduisons-en que $N$ est le milieu de $[IT].$
En considérant le triangle $IRT$, nous constatons que la droite $(NP)$ passant par $P$ et parallèle à la droite $(RT)$ coupe $[IT]$ en $N.$
Comme $P$ est milieu de $[IR]$ alors, d'après la réciproque du théorème de la droite des milieux, $N$ est milieu de $[IT].$
Exercice 20
Soit $ABC$ un triangle, on appelle $I$ le milieu de $[BC]\;,\ J$ le milieu de $[AB]\ $ et $\ K$ le milieu de $[AI].$
Soit $L$ le point d'intersection de $(JK)\ $ et $\ (AC).$
1) Faisons une figure complète.

2) Démontrons que $(JK)\parallel(BC).$
Considérons le triangle $ABI.$
On a : la droite $(JK)$ passe par les points $J\ $ et $\ K$ ; milieux respectifs des côtés $[AB]\ $ et $\ [AI].$
Or, d'après le théorème de la droite des milieux, on sait que : dans un triangle, la droite qui passe par les milieux des deux côtés est parallèle au troisième côté.
Donc, en appliquant le théorème de la droite des milieux sur le triangle $ABI$, on obtient : $(JK)$ parallèle à $(BI).$
Par conséquent, $(JK)\parallel(BC)$ car, $B\;,\ I\ $ et $\ C$ sont alignés.
3) Démontrons que $L$ est le milieu de $(AC).$
Considérons le triangle $ABC.$
Alors, on a : $J$ milieu de $[AB]$ et la droite $(JK)$ passant par $J$ et parallèle à la droite $(BC)$, coupe $[AC]$ en $L.$
Or, d'après la réciproque du théorème de la droite des milieux, on sait que : dans un triangle si, une droite est parallèle à un côté et si, elle passe par le milieu d'un deuxième côté alors, elle passe par le milieu du troisième côté.
Donc, d'après la réciproque du théorème de la droite des milieux, $L$ est milieu de $[AC].$
4) On appelle $M$ le milieu de $[IC].$
Montrons que $JK=KL=IM.$
En effet, d'après une conséquence du théorème de la droite des milieux, on sait que : dans un triangle, le segment joignant les milieux de deux côtés a pour longueur la moitié de la longueur du troisième côté.
Alors, en considérant le triangle $AIC$, on a : $K$ milieu de $[AI]\ $ et $\ L$ celui de $[AC].$
Par conséquent,
$$KL=\dfrac{IC}{2}$$
Par ailleurs, comme $M$ est le milieu de $[IC]$ alors,
$$IM=\dfrac{IC}{2}$$
De la même manière, en considérant le triangle $ABI$, on a : $J$ milieu de $[AB]\ $ et $\ K$ celui de $[AI]$ alors, $JK=\dfrac{BI}{2}$
Or, $I$ est le milieu de $[BC]$ donc, $BI=IC.$
Par suite, en remplaçant $BI$ par $IC$, on obtient :
$$JK=\dfrac{BC}{2}=\dfrac{IC}{2}$$
Ainsi, on a :
$$\left\lbrace\begin{array}{rcl} KL&=&\dfrac{IC}{2}\\\\IM&=&\dfrac{IC}{2}\\\\JK&=&\dfrac{IC}{2}\end{array}\right.$$
Par conséquent, $\boxed{JK=KL=IM}$

Exercice 21
Dans la figure ci-dessous, $ABC$ est un triangle tel que $D\ $ et $\ E$ appartiennent à $(AB)\;,\ G\ $ et $\ F$ appartiennent à $(BC)\;,\ K$ point d'intersection des droites $(GD)\ $ et $\ (AF).$

1) Montrons que $(EF)\ $ et $\ (GD)$ sont parallèles.
En considérant le triangle $BDG$, on remarque que $F$ est milieu de $[GB]\ $ et $\ E$ celui de $[BD].$
Donc, la droite $(EF)$ passe par les points $E\ $ et $\ F$ ; milieux respectifs des côtés $[BD]\ $ et $\ [GB]$ de ce triangle.
Or, d'après le théorème de la droite des milieux, on sait que : dans un triangle, la droite qui passe par les milieux des deux côtés est parallèle au troisième côté.
Par conséquent, les droites $(EF)\ $ et $\ (GD)$ sont parallèles.
2) Montrons que $K$ est le milieu de $[AF].$
En considérant le triangle $AEF$, on constate que $D$ est milieu de $[AE].$
Alors, la droite $(GD)$ passant par $D$ et parallèle à la droite $(EF)$, coupe $[AF]$ en $K.$
Or, d'après la réciproque du théorème de la droite des milieux, on sait que : dans un triangle si, une droite est parallèle à un côté et si, elle passe par le milieu d'un deuxième côté alors, elle passe par le milieu du troisième côté.
Donc, d'après la réciproque du théorème de la droite des milieux, $K$ est le milieu de $[AF].$
3) Comparons $DK\ $ et $\ DG.$
En effet,
En effet, d'après une conséquence du théorème de la droite des milieux, on sait que : dans un triangle, le segment joignant les milieux de deux côtés a pour longueur la moitié de la longueur du troisième côté.
Alors, en considérant le triangle $AEF$, on a : $K$ milieu de $[AF]\ $ et $\ D$ celui de $[AE].$
Par conséquent, $DK=\dfrac{EF}{2}$
Ce qui donne : $EF=2DK$
De la même manière, en considérant le triangle $BDG$, on a : $E$ milieu de $[BD]\ $ et $\ F$ celui de $[GB].$
D'où, $EF=\dfrac{DG}{2}$
Ainsi, dans cette dernière égalité, en remplaçant $EF$ par $2DK$, on obtient :
$\begin{array}{rcl} EF=\dfrac{DG}{2}&\Rightarrow&2DK=\dfrac{DG}{2}\\\\&\Rightarrow&2\times 2DK=DG\\\\&\Rightarrow&4DK=DG\end{array}$
D'où, $\boxed{DG=4DK}$
4) Montrons que $(DG)\ $ et $\ (AC)$ sont parallèles.
En considérant le triangle $ACF$, on a : $G$ milieu de $[CF]\ $ et $\ K$ celui de $[AF].$
Donc, d'après le théorème de la droite des milieux, les droites $(GK)\ $ et $\ (AC)$ sont parallèles.
Ce qui signifie que $(DG)\ $ et $\ (AC)$ sont parallèles.
Exercice 22
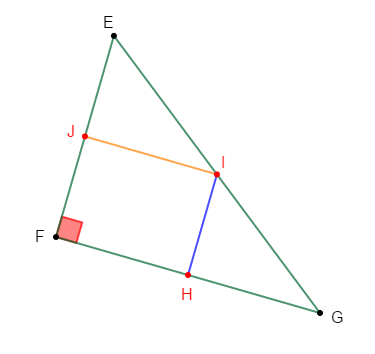
$EFG$ est un triangle rectangle en $F.$
Les points $H\;,\ I\ $ et $\ J$ sont les milieux respectifs des côtés $[FG]\;,\ [GE]\ $ et $\ [EF].$
Démontrons que le quadrilatère $FHIJ$ est un rectangle.
En effet, dans le triangle $EFG$ on a : $I$ milieu de $[GE]\ $ et $\ J$ milieu de $[EF].$
Donc, d'après le théorème de la droite des milieux, la droite $(IJ)$ est parallèle à la droite $(FG).$
D'où, $(IJ)$ parallèle à $(FH)$
De la même manière, on a : $I$ milieu de $[GE]\ $ et $\ H$ milieu de $[FG].$
Alors, d'après le théorème de la droite des milieux, la droite $(IH)$ est parallèle à la droite $(EF).$
Par suite, $(IH)$ parallèle à $(JF)$
Ainsi, on a :
$$\left\lbrace\begin{array}{r} (IJ)\parallel(FH)\\\\(IH)\parallel(JF)\end{array}\right.$$
Donc, le quadrilatère $FHIJ$ a ses côtés parallèles $2$ à $2.$
Alors, c'est un parallélogramme.
Par ailleurs, on sait que : si, un parallélogramme a un angle droit alors, c'est un rectangle
Or, le triangle $EFG$ étant rectangle en $F$ alors, l'angle $\widehat{F}$ est un angle droit.
Par conséquent, $FHIJ$ est un rectangle.

Exercice 23
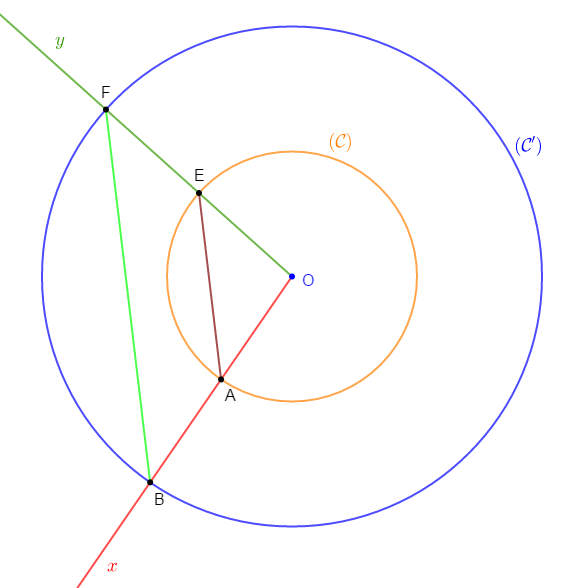
$(\mathcal{C})\ $ et $\ (\mathcal{C}')$ sont deux cercles de centre $O$ dont les rayons sont respectivement $2.5\;cm\ $ et $\ 5\;cm.$
Une demi-droite $[Ox)$ coupe $(\mathcal{C})$ au point $A\ $ et $\ (\mathcal{C}')$ au point $B.$
Une autre demi-droite $[Oy)$ non opposée à $[Ox)$ coupe $(\mathcal{C})$ au point $E\ $ et $\ (\mathcal{C}')$ au point $F.$
1) Démontrons que $BF=2AE.$
En effet, comme le rayon du cercle $(\mathcal{C}')$ est le double de celui du cercle $(\mathcal{C})$ alors, on a :
$OF=2OE$ ; ce qui signifie que $E$ est le milieu de $[OF]$
$OB=2OA$ ; ce qui veut dire que $A$ est le milieu de $[OB]$
Or, d'après une conséquence du théorème de la droite des milieux, on sait que : dans un triangle, le segment joignant les milieux de deux côtés a pour longueur la moitié de la longueur du troisième côté.
Donc, en appliquant cette propriété au triangle $OBF$, on obtient :
$$AE=\dfrac{BF}{2}$$
Ce qui donne alors :
$$BF=2AE$$
2) $ABFE$ est un trapèze
Justification :
En effet, dans le triangle $OBF$, nous constatons que la droite $(AE)$ passe par $A\ $ et $\ E$ ; milieux respectifs des côtés $[OB]\ $ et $\ [OF].$
Donc, en appliquant le théorème de la droite des milieux sur le triangle $OBF$, on obtient : $(AE)$ parallèle à $(BF).$
De plus, d'après la question $1)$, on a : $BF=2AE$ donc, les segments $[BF]\ $ et $\ [AE]$ n'ont pas la même longueur.
Ainsi, $ABFE$ est un quadrilatère dont deux côtés sont parallèles et de longueurs différentes.
Par conséquent, $ABFE$ est un trapèze.

Auteur:
Diny Faye

Commentaires
Aladji (non vérifié)
jeu, 01/30/2020 - 18:16
Permalien
Aba48932@gmail.com
MAMADOU SALIOU BALDE (non vérifié)
ven, 03/26/2021 - 23:08
Permalien
tous les exercices des droites des milieux
Cheikhouna Bousso (non vérifié)
jeu, 02/06/2020 - 01:50
Permalien
J'aimerais voir tous la
Cheikhouna Bousso (non vérifié)
jeu, 02/06/2020 - 01:54
Permalien
J'aimerais voir tous les
Anonyme (non vérifié)
mar, 12/01/2020 - 21:24
Permalien
Bonsoir je voulais la
MAMADOU SALIOU BALDE (non vérifié)
ven, 03/26/2021 - 23:09
Permalien
tous les exercices des droites des milieux
Anonyme (non vérifié)
ven, 02/05/2021 - 20:56
Permalien
pour le PGDC il faut dadort
Anonyme (non vérifié)
ven, 02/05/2021 - 20:56
Permalien
pour le PGDC il faut dadort
Anonyme (non vérifié)
ven, 02/05/2021 - 20:56
Permalien
pour le PGDC il faut dadort
Anonyme (non vérifié)
ven, 02/05/2021 - 20:56
Permalien
pour le PGDC il faut dadort
Mouhamed (non vérifié)
mar, 04/13/2021 - 19:51
Permalien
Telechargement
Absa (non vérifié)
ven, 05/07/2021 - 00:30
Permalien
J'aimerais avoir la
Ajouter un commentaire