Solution des exercices : Systèmes d'équations à deux inconnues 3e
Classe:
Troisième
Exercice 1
1) Soit l'équation $2x-y+2=0$ alors, un couple $(a\;,\ b)$ est solution de cette équation si, et seulement si, ce couple vérifie l'équation ; c'est à dire si, $2a-b+2=0.$
Pour le couple $(-2\;;\ 1)$ on a : $2\times(-2)-1+2=-4-1+2=-3\neq 0$
Donc, ce couple ne vérifiant pas l'équation, alors $(-2\;;\ 1)$ n'est pas solution de $2x-y+2=0.$
Pour le couple $(0\;;\ -2)$ on a : $2\times(0)-(-2)+2=0+2+2=4\neq 0$
Ce couple ne vérifiant pas l'équation alors, $(0\;;\ -2)$ n'est pas solution de $2x-y+2=0.$
Pour le couple $(-2\;;\ 0)$ on a : $2\times(-2)-(0)+2=-4+2=-2\neq 0$
Donc, ce couple ne vérifiant pas l'équation alors, $(-2\;;\ 0)$ n'est pas solution de $2x-y+2=0.$
Pour le couple $(-4\;;\ -6)$, on a : $2\times(-4)-(-6)+2=-8+6+2=-8+8=0$
On voit que ce couple vérifie l'équation.
Donc, $(-4\;;\ -6)$ est solution de $2x-y+2=0.$
2) a) $(-1\;,\ 0)$ et $(2\;,\ 2)$ sont deux couples, solutions de l'équation $2x-3y+2=0$
b) $(0\;,\ 0)$ et $(1\;,\ 2)$ sont deux couples, solutions de l'équation $2x-y=0$
Exercice 2
On sait que :
$-\ $ Un couple est solution d'un système d'équations s'il vérifie les équations du système.
$-\ $ Si un couple ne vérifie pas une des équations du système alors, ce couple n'est pas solution de ce système.
1) Le couple $\left(\dfrac{3}{2}\;;\ \dfrac{-1}{2}\right)$ est solution du système
$$\left\lbrace\begin{array}{rcl} x-y-2&=&0 \\ -x-y+1&=&0\end{array}\right.\qquad vrai$$
En effet, $\dfrac{3}{2}-\dfrac{-1}{2}-2=\dfrac{3}{2}+\dfrac{1}{2}-\dfrac{4}{2}=0$, donc le couple de points $\left(\dfrac{3}{2}\;;\ \dfrac{-1}{2}\right)$ vérifie la première équation.
Aussi, $-\dfrac{3}{2}-\dfrac{-1}{2}+1=-\dfrac{3}{2}+\dfrac{1}{2}+\dfrac{2}{2}=0$
Donc, le couple $\left(\dfrac{3}{2}\;;\ \dfrac{-1}{2}\right)$ vérifie également la deuxième équation.
D'où, Le couple $\left(\dfrac{3}{2}\;;\ \dfrac{-1}{2}\right)$ est solution du système $$\left\lbrace\begin{array}{rcl} x-y-2&=&0 \\ -x-y+1&=&0\end{array}\right.$$
2) Le couple $(\sqrt{2}\;;\ \sqrt{3})$ est solution de ce système
$$\left\lbrace\begin{array}{rcl} \sqrt{2}x-\sqrt{3}y-2&=&-1 \\ \sqrt{6}x+3y&=&4\sqrt{3}\end{array}\right.\qquad faux$$
En effet, on a : $\sqrt{2}\times\sqrt{2}-\sqrt{3}\times\sqrt{3}-2=2-3-2=-3\neq -1$
Alors, le couple $(\sqrt{2}\;;\ \sqrt{3})$ ne vérifie pas la première équation.
Donc, le couple $(\sqrt{2}\;;\ \sqrt{3})$ n'est pas solution du système $$\left\lbrace\begin{array}{rcl} \sqrt{2}x-\sqrt{3}y-2&=&-1 \\ \sqrt{6}x+3y&=&4\sqrt{3}\end{array}\right.$$
Exercice 3
On se propose de résoudre dans $\mathbb{R}\times\mathbb{R}$ chacun des systèmes d'équations suivants par la "méthode de substitution" :
Méthode :
$-\ $ choisir une équation et exprimer l'une des inconnues en fonction de l'autre dans cette équation
$-\ $ remplacer l'expression de cette inconnue dans l'autre équation afin d'obtenir une équation du 1er degré à une inconnue
$-\ $ résoudre cette équation du 1er degré et trouver la valeur de l'inconnue
$-\ $ remplacer cette valeur de l'inconnue trouvée dans l'équation choisie au départ afin de déterminer la valeur de l'autre inconnue.
Ainsi, ce couple de valeurs va constituer la solution du système.
1) Soit à résoudre le système suivant
$$\left\lbrace\begin{array}{rcl} x-y+3&=&0\qquad(1) \\ 2x+y-6&=&0\qquad(2)\end{array}\right.$$
Exprimons $x$ en fonction de $y$ dans l'équation (1). On a alors : $x=y-3.$
Remplaçons cette expression de $x$ dans l'équation (2).
Cela donne : $2(y-3)+y-6=0.$
En développant on obtient : $2y-6+y-6=0$
Ainsi, $3y=12$ ; par suite $y=\dfrac{12}{3}=4$
Remplaçons maintenant cette valeur de $y$ dans l'équation (1) pour déterminer celle de $x.$
On obtient alors : $x-4+3=0$
Ainsi, $x-1=0$ ; par suite $x=1$
D'où $$S=\{(1\;;\ 4)\}$$
2) Soit à résoudre le système
$$\left\lbrace\begin{array}{rcl} x+2y-11&=&0\qquad(1)\\ 2x+3y-5&=&0 \qquad(2)\end{array}\right.$$
Exprimons $x$ en fonction de $y$ dans l'équation (1). On a alors : $x=-2y+11.$
Remplaçons cette expression de $x$ dans l'équation (2).
Cela donne : $2(-2y+11)+3y-5=0.$
Ainsi, $-4y+22+3y-5=0$
Ce qui donne : $-y=-17$ ; c'est-à-dire $y=17$
Remplaçons maintenant cette valeur de $y$ dans l'équation (1) pour trouver celle de $x.$
On obtient alors : $x+2\times 17-11=0$
Donc, $x+34-11=0$
Ainsi, $x+23=0$ ; par suite $x=-23$
D'où $$S=\{(-23\;;\ 17)\}$$
3) Soit le système suivant
$$\left\lbrace\begin{array}{rcr} 2x-3y&=&0\qquad(1)\\ x+y&=&-4\qquad(2)\end{array}\right.$$
Exprimons $x$ en fonction de $y$ dans l'équation (2). On a alors : $x=-y-4.$
Remplaçons cette expression de $x$ dans l'équation (1).
Cela donne : $2(-y-4)-3y=0.$
Ainsi, $-2y-8-3y=0$
par suite, $-5y=8$ ; par conséquent $y=\dfrac{8}{-5}=-\dfrac{8}{5}$
Remplaçons maintenant cette valeur de $y$ dans l'équation (2) pour trouver la valeur de $x.$
On obtient alors : $x-\dfrac{8}{5}=-4$
donc, $x=-4+\dfrac{8}{5}$
ainsi, $x=\dfrac{-20}{5}+\dfrac{8}{5}=\dfrac{-20+8}{5}$ ;
par suite, $x=\dfrac{-12}{5}=-\dfrac{12}{5}$
D'où $$S=\left\{\left(-\dfrac{12}{5}\;;\ -\dfrac{8}{5}\right)\right\}$$
4) Soit à résoudre le système suivant
$$\left\lbrace\begin{array}{rcr} 4x-3y&=&1\\ 12x-y&=&-5\end{array}\right.$$
On procède comme dans les questions 1, 2, 3
On trouve $$S=\left\{\left(-\dfrac{1}{2}\;;\ -1\right)\right\}$$
5) Soit à résoudre le système suivant
$$\left\lbrace\begin{array}{rcl} x+y-6&=&0\\ 5x-2y&=&8\end{array}\right.$$
On procède comme dans les questions 1, 2, 3
Ainsi, la solution de ce système est donnée par $$S=\left\{\left(\dfrac{8}{7}\;;\ -\dfrac{8}{7}\right)\right\}$$
6) Soit à résoudre le système suivant
$$\left\lbrace\begin{array}{rcl} x-\sqrt{2}y&=&2\\ x+\sqrt{2}y-\sqrt{3}&=&0\end{array}\right.$$
On procède comme dans les questions 1, 2, 3
Ainsi, la solution est $$S=\left\{\left(\dfrac{2+\sqrt{3}}{2}\;;\ \dfrac{-2\sqrt{2}+\sqrt{6}}{4}\right)\right\}$$
Exercice 4
On se propose de résoudre dans $\mathbb{R}^{2}$ les systèmes suivants par la "méthode de comparaison" :
Méthode :
$-\ $ pour chacune des deux équations, exprimer l'une des inconnues en fonction de l'autre
$-\ $ comparer les deux égalités obtenues pour trouver l'une des inconnues
$-\ $ remplacer la valeur de l'inconnue trouvée dans l'une des équations afin de déterminer la valeur de l'autre inconnue.
Ainsi, ce couple de valeurs va constituer la solution du système.
1) Soit à résoudre le système suivant
$$\left\lbrace\begin{array}{rcl} x-y&=&7\qquad(1)\\ x+y&=&3\qquad(2)\end{array}\right.$$
Dans les équations (1) et (2), exprimons $x$ en fonction de $y.$
On a : $$\left\lbrace\begin{array}{rcl} x&=&7+y\qquad(3)\\ x&=&3-y\qquad(4)\end{array}\right.$$
La comparaison des équations (3) et (4) donne : $7+y=3-y$
donc, $2y=3-7=-4$
par suite, $y=\dfrac{-4}{2}=-2$
En remplaçant cette valeur de $y$ dans l'équation (1) on obtient :
$x-(-2)=7$ c'est-à-dire $x+2=7$
donc, $x=7-2=5$
Ainsi, $$S=\{(5\;;\ -2)\}$$
Remarque : on peut aussi remplacer la valeur de $y$ directement dans les équations (3) ou (4) afin de trouver plus rapidement la valeur de $x.$
2) Soit à résoudre le système
$$\left\lbrace\begin{array}{rcl} x-y-5&=&0\qquad(1)\\ x+2y&=&4\qquad(2)\end{array}\right.$$
Exprimons $x$ en fonction de $y$ dans les équations (1) et (2).
On a : $$\left\lbrace\begin{array}{rcr} x&=&y+5\qquad(3)\\ x&=&4-2y\qquad(4)\end{array}\right.$$
Comparons les équations (3) et (4).
On a alors : $y+5=4-2y$
donc, $3y=4-5=-1$
par suite, $y=\dfrac{-1}{3}$
En remplaçant cette valeur de $y$ dans l'équation (3) on obtient :
$x=-\dfrac{1}{3}+5$
cela donne : $x=\dfrac{14}{3}$
D'où, $$S=\left\{\left(\dfrac{14}{3}\;;\ -\dfrac{1}{3}\right)\right\}$$
3) Soit à résoudre le système
$$\left\lbrace\begin{array}{rcr} 2y+x&=&5\qquad(1)\\ -y+7&=&x+4\qquad(2)\end{array}\right.$$
Dans les équations (1) et (2), exprimons $x$ en fonction de $y.$
On a : $$\left\lbrace\begin{array}{rcr} x&=&5-2y\qquad(3)\\ x&=&-y+7-4\qquad(4)\end{array}\right.$$
La comparaison des équations (3) et (4) donne : $5-2y=-y+3$
alors, $-y=-2$, c'est-à-dire $y=2$
En remplaçant cette valeur de $y$ dans l'équation (4) on obtient :
$x=-2+7-4$ c'est-à-dire $x=-6+7$
donc, $x=1$
Ainsi, $$S=\{(1\;;\ 2)\}$$
4) Soit à résoudre le système
$$\left\lbrace\begin{array}{rcl} 3x-y&=&2\\ 2x-y&=&1\end{array}\right.$$
En appliquant la même méthode que dans les questions 1, 2, 3, on obtient :
$$S=\{(1\;;\ 1)\}$$
5) Soit à résoudre le système
$$\left\lbrace\begin{array}{rcl} x-2y&=&6\\ -x+y&=&-4\end{array}\right.$$
En appliquant la même méthode que dans les questions 1, 2, 3, on obtient :
$$S=\{(2\;;\ -2)\}$$
6) Soit à résoudre le système
$$\left\lbrace\begin{array}{rcl} x-3y-3&=&0\\ 3x-2y+4&=&0\end{array}\right.$$
En appliquant la même méthode que dans les questions 1, 2, 3, on obtient :
$$S=\left\{\left(-\dfrac{18}{7}\;;\ -\dfrac{13}{7}\right)\right\}$$
Exercice 5
On se propose de résoudre dans $\mathbb{R}\times\mathbb{R}$ les systèmes d'équations suivants par la "méthode de combinaison ou d'addition" :
Méthode :
$-\ $ multiplier éventuellement les équations par des coefficients de sorte qu'en les additionnant l'on obtienne une équation à une inconnue
$-\ $ après multiplication de coefficients, additionner les équations
$-\ $ résoudre l'équation à une inconnue obtenue afin de trouver la valeur de l'inconnue
$-\ $ remplacer cette valeur de l'inconnue dans l'une des équations de départ pour trouver la valeur de l'autre inconnue.
Ainsi, ce couple de valeurs va constituer la solution du système.
1) Soit à résoudre le système suivant
$$\left\lbrace\begin{array}{rcl} x-y&=&7\qquad(1)\\ 2x+3y&=&1\qquad(2)\end{array}\right.$$
En multipliant donc l'équation (1) par -2 et l'équation (2) par 1 on obtient :
$$\left\lbrace\begin{array}{rcr} -2x+2y&=&-14\qquad(3)\\ 2x+3y&=&1\qquad(4)\end{array}\right.$$
En "additionnant" l'équation (3) et l'équation (4) on aura :
$-2x+2y+2x+3y=-14+1$
Cela donne : $5y=-13$
donc, $y=-\dfrac{13}{5}$
En remplaçant cette valeur de $y$ dans l'équation (1), on obtient :
$x-\left(-\dfrac{13}{5}\right)=7$
donc, $x=7-\dfrac{13}{5}=\dfrac{22}{5}$
Ainsi, $$S=\left\{\left(\dfrac{22}{5}\;;\ -\dfrac{13}{5}\right)\right\}$$
2) Soit à résoudre le système
$$\left\lbrace\begin{array}{rcl} 3x+7y-5&=&0\qquad(1)\\ 5x-3y+3&=&0\qquad(2)\end{array}\right.$$
En multipliant donc l'équation (1) par 5 et l'équation (2) par -3 on obtient :
$$\left\lbrace\begin{array}{rcl} 15x+35y-25&=&0\qquad(3)\\ -15x+9y-9&=&0\qquad(4)\end{array}\right.$$
En "additionnant" l'équation (3) et l'équation (4) on aura :
$15x+35y-25-15x+9y-9=0$
c'est-à-dire $44y-34=0$, ou encore $44y=34$
donc, $y=\dfrac{34}{44}$ et en simplifiant on trouve $y=\dfrac{17}{22}$
En remplaçant cette valeur de $y$ dans l'équation (1), on obtient :
$3x+7\left(\dfrac{17}{22}\right)-5=0$
donc, $3x=5-\dfrac{119}{22}=-\dfrac{9}{22}$
d'où $x=\dfrac{-\dfrac{9}{22}}{3}=-\dfrac{9}{22}\times\dfrac{1}{3}=-\dfrac{3}{22}$
Ainsi, $$S=\left\{\left(-\dfrac{3}{22}\;;\ \dfrac{17}{22}\right)\right\}$$
3) Soit à résoudre le système suivant
$$\left\lbrace\begin{array}{rcl} 4x-3y&=&0\qquad(1)\\ 3x-2y&=&1\qquad(2)\end{array}\right.$$
En multipliant donc l'équation (1) par -2 et l'équation (2) par 3 on obtient :
$$\left\lbrace\begin{array}{rcr} -8x+6y&=&0\qquad(3)\\ 9x-6y&=&3\qquad(4)\end{array}\right.$$
En "additionnant" l'équation (3) et l'équation (4) on aura :
$-8x+6y+9x-6y=3$
Cela donne : $x=3$
En remplaçant cette valeur de $x$ dans l'équation (1), on obtient :
$4\times 3-3y=0$
donc, $-3y=-12$
d'où $y=\dfrac{12}{3}=4$
Ainsi, $$S=\{(3\;;\ 4)\}$$
4) Soit à résoudre le système suivant
$$\left\lbrace\begin{array}{rcl} 7x+3y&=&1\qquad(1)\\ x-3y&=&7\qquad(2)\end{array}\right.$$
En observant bien ce système, on constate qu'en additionnant les équations (1) et (2) on obtient une équation à une inconnue car les termes en $y$ vont se neutraliser.
On a alors : $7x+3y+x-3y=1+7$
donc, $8x=8$
d'où $x=1$
En remplaçant cette valeur de $x$ dans l'équation (1), on obtient :
$7\times 1+3y=1$
donc, $3y=1-7=-6$
d'où $y=-\dfrac{6}{3}=-2$
Ainsi, $$S=\{(1\;;\ -2)\}$$
5) Soit à résoudre le système suivant
$$\left\lbrace\begin{array}{rcl} 5x+3y-6&=&0\qquad(1)\\ -5x+2y-1&=&0\qquad(2)\end{array}\right.$$
Là encore, il suffit d'additionner les deux équations pour obtenir une équation à une inconnue.
On a alors : $5x+3y-6-5x+2y-1=0$
donc, $5y-7=0$ ; c'est-à-dire $5y=7$
d'où, $y=\dfrac{7}{5}$
En remplaçant cette valeur de $y$ dans l'équation (1), on obtient :
$5x+3\left(\dfrac{7}{5}\right)-6=0$
donc, $5x=6-\dfrac{21}{5}=\dfrac{30-21}{5}=\dfrac{9}{5}$
d'où $x=\dfrac{\dfrac{9}{5}}{5}=\dfrac{9}{5}\times\dfrac{1}{5}=\dfrac{9}{25}$
Ainsi, $$S=\left\{\left(\dfrac{9}{25}\;;\ \dfrac{7}{5}\right)\right\}$$
6) Soit à résoudre le système suivant
$$\left\lbrace\begin{array}{rcl} 2x+2y&=&1\\ 3x-3y&=&-2\end{array}\right.$$
En appliquant la même méthode que dans les questions 1, 2, 3, on obtient :
$$S=\left\{\left(-\dfrac{1}{12}\;;\ \dfrac{7}{12}\right)\right\}$$
Exercice 6
1) Résolvons algébriquement dans $\mathbb{R}\times\mathbb{R}$ le système d'équations défini par : $$\left\lbrace\begin{array}{rcl} x-y-1&=&0\qquad(1)\\ 2x-y+2&=&0\qquad(2)\\ -x+3y+9&=&0\qquad(3)\end{array}\right.$$
Méthode :
$-\ $ choisir deux équations
$-\ $ résoudre le système composé de ces deux équations
$-\ $ vérifier avec le couple de solutions dans l'équation non choisie.
Considérons les équations (1) et (3).
Alors, on a le système suivant : $$\left\lbrace\begin{array}{rcl} x-y-1&=&0\qquad(1)\\ -x+3y+9&=&0\qquad(3)\end{array}\right.$$
On procède par la méthode de combinaison en additionnant les équations (1) et (3).
Cela donne : $x-y-1-x+3y+9=0$
donc, $2y+8=0$ ; par suite , $2y=-8$
d'où, $y=-\dfrac{8}{2}=-4$
En remplaçant cette valeur de $y$ dans l'équation (1) on obtient :
$x-(-4)-1=0$ ; soit $x=-3$
Regardons maintenant si ces valeurs de $x$ et $y$ vérifient l'équation (2).
On a : $2\times(-3)-(-4)+2=-6+4+2=-6+6=0$
Ce qui montre que ces valeurs vérifient bien l'équation (2).
Donc, $$S=\{(-3\;;\ -4)\}$$
2) Interprétons géométriquement cette réponse dans un repère orthonormé $(O\;,\ I\;,\ J).$
Considérons les droites $(D_{1})\;,\ (D_{2})$ et $(D_{3})$ d'équations respectives les équations du système.
On a alors :
$(D_{1})\;:\ x-y-1=0\;,\ (D_{2})\;:\ 2x-y+2=0$ et $(D_{3})\;:\ -x+3y+9=0$
Dans un repère orthonormé $(O\;,\ I\;,\ J)$, le couple de valeurs ; solutions du système, constitue les cordonnées du point d'intersection de ces trois droites.
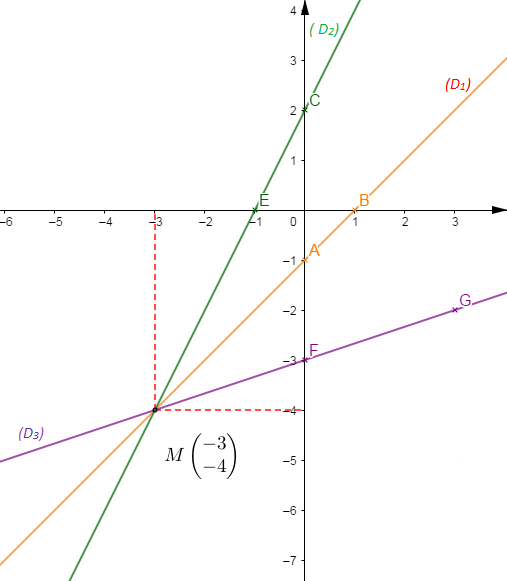
Donc, si $M=(D_{1})\cap (D_{2})\cap (D_{3})$ alors on aura : $$M\begin{pmatrix} -3 \\ -4\end{pmatrix}$$
Illustration :
Illustration :
Pour tracer chaque droite on choisit deux points.
Soit $A\;,\ B\in (D_{1})\;,\ C\;,\ E\in (D_{2})\ $ et $\ F\;,\ G\in (D_{3})$
On a :
$$\begin{array}{|c|c|c|}\hline & A & B \\ \hline x & 0 & 1 \\ \hline y & -1 & 0 \\ \hline\end{array}\qquad\qquad \begin{array}{|c|c|c|}\hline & C & E \\ \hline x & 0 & -1 \\ \hline y & 2 & 0 \\ \hline\end{array}\qquad\qquad \begin{array}{|c|c|c|}\hline & F & G \\ \hline x & 0 & 3 \\ \hline y & -3 & -2 \\ \hline\end{array}$$

Le point $M\begin{pmatrix} -3 \\ -4\end{pmatrix}$ est la solution graphique du système.
On remarque que le couple de valeurs ; solution du système, représente les cordonnées du point $M$, point d'intersection des trois droites.
Exercice 7
Résolvons dans $\mathbb{R}\times\mathbb{R}$ les systèmes d'équations suivants par la "méthode graphique" :
1) $\left\lbrace\begin{array}{rcl} 2x-y-1&=&0\qquad(1)\\ x-y+4&=&0\qquad(2)\end{array}\right.$
Considérons les droites $(D_{1})$ et $(D_{2})$ d'équations respectives les équations (1) et (2) du système.
On a alors :
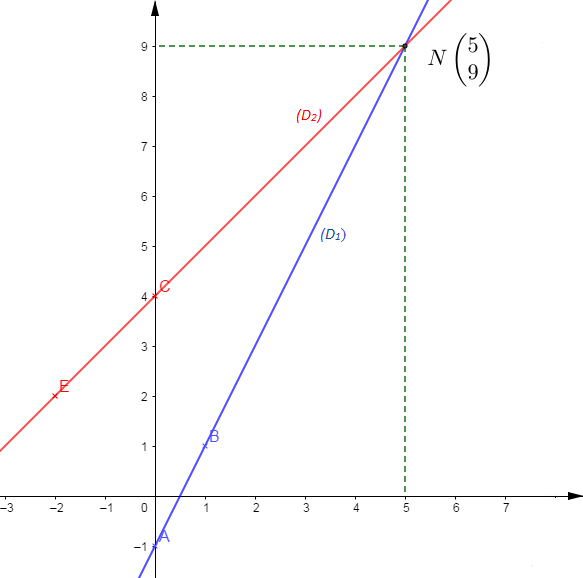
$(D_{1})\;:\ 2x-y-1=0\quad$ et $\quad(D_{2})\;:\ x-y+4=0$
Traçons ces deux droites dans un repère orthonormé $(O\;,\ I\;,\ J).$
Pour cela, on choisit, pour chaque droite, deux points dont les coordonnées vérifient l'équation de la droite.
Soit $A\;,\ B\in (D_{1})\ $ et $\ C\;,\ E\in (D_{2})$
On a :
$$\begin{array}{|c|c|c|}\hline & A & B \\ \hline x & 0 & 1 \\ \hline y & -1 & 1 \\ \hline\end{array}\qquad\qquad \begin{array}{|c|c|c|}\hline & C & E \\ \hline x & 0 & -2 \\ \hline y & 4 & 2 \\ \hline\end{array}$$

Le point $N\begin{pmatrix} 5 \\ 9\end{pmatrix}$ est la solution du système par la méthode graphique.
2) $\left\lbrace\begin{array}{rcl} x-2y+4&=&0\qquad(1)\\ -2x+4y-8&=&0\qquad(2)\end{array}\right.$
Nous remarquons qu'en multipliant l'équation (1) par $-2$, on obtient l'équation (2).
Donc, les droites $(D_{1})$ et $(D_{2})$ d'équations respectives les équations (1) et (2) du système sont confondues.
Ainsi, la solution graphique de ce système n'est rien d'autre que la représentation graphique de $(D_{1})\ $ ou $\ (D_{2}).$
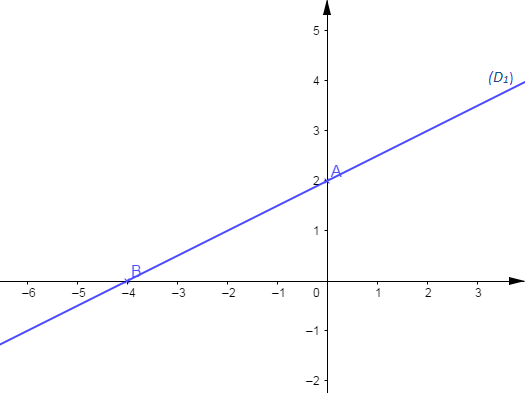
Soit alors $(D_{1})\ :\ x-2y+4=0$
Pour tracer cette droite on choisit deux points dont les coordonnées vérifient l'équation de la droite.
Soit $A\;,\ B\in (D_{1})$
On a :
$$\begin{array}{|c|c|c|}\hline & A & B \\ \hline x & 0 & -4 \\ \hline y & 2 & 0 \\ \hline\end{array}$$

Exercice 8
Résolvons les systèmes d'équations suivants :
1) Soit le système suivant :
$$\left\lbrace\begin{array}{rclr} x^{2}+y^{2}&=&41&\qquad(1)\\\\x^{2}-y^{2}&=&9&\qquad(2)\end{array}\right.$$
Pour résoudre ce système, on peut utiliser la méthode d'addition.
Alors, en additionnant membre à membre les équations $(1)\ $ $(2)$, on obtient :
$$x^{2}+y^{2}+x^{2}-y^{2}=41+9$$
Ce qui donne : $2x^{2}=50$
En résolvant cette équation, on trouve :
$\begin{array}{rcl} 2x^{2}=50&\Leftrightarrow&x^{2}=\dfrac{50}{2}\\\\&\Leftrightarrow&x^{2}=25\\\\&\Leftrightarrow&\sqrt{x^{2}}=\sqrt{25}\\\\&\Leftrightarrow&|x|=5\\\\&\Leftrightarrow&x=5\ \text{ ou }\ x=-5\end{array}$
Donc, $\boxed{x=5\ \text{ ou }\ x=-5}$
Ainsi, dans l'équation $(1)$, en remplaçant $x$ par $5$, on obtient :
$$5^{2}+y^{2}=41$$
C'est-à-dire ; $25+y^{2}=41$
Ce qui donne : $y^{2}=41-25=16$
En résolvant cette équation, on trouve :
$\begin{array}{rcl} y^{2}=16&\Leftrightarrow&\sqrt{y^{2}}=\sqrt{16}\\\\&\Leftrightarrow&|y|=4\\\\&\Leftrightarrow&y=4\ \text{ ou }\ x=-4\end{array}$
Donc, $\boxed{y=4\ \text{ ou }\ y=-4}$
Ainsi, les couples : $(5\;;\ 4)\ $ et $\ (5\;;\ -4)$ sont solutions du système.
De la même manière, en remplaçant $x$ par $-5$ dans l'équation $(1)$, on obtient :
$$(-5)^{2}+y^{2}=41$$
Ce qui donne : $25+y^{2}=41$
Ce qui entraine : $y^{2}=16$
En résolvant cette équation, on trouve : $\boxed{y=4\ \text{ ou }\ y=-4}$
Donc, les couples : $(-5\;;\ 4)\ $ et $\ (-5\;;\ -4)$ sont aussi solutions du système.
Par conséquent, le système d'équations : $\left\lbrace\begin{array}{rcl} x^{2}+y^{2}&=&41\\\\x^{2}-y^{2}&=&9\end{array}\right.$ a pour solution dans $\mathbb{R}\times\mathbb{R}\ :$
$$S=\left\{(5\;;\ 4)\;,\ (5\;;\ -4)\;,\ (-5\;;\ 4)\;,\ (-5\;;\ -4)\right\}$$
2) Soit à résoudre le système suivant :
$$\left\lbrace\begin{array}{rclr}\dfrac{2}{x}-\dfrac{1}{y}&=&\dfrac{3}{5}&\qquad(1)\\ \\ \dfrac{1}{x}+\dfrac{1}{y}&=&\dfrac{7}{5}&\qquad(2)\end{array}\right.$$
Il faut rappeler que ce système existe si, et seulement si, $x\neq 0\ $ et $\ y\neq 0.$
Pour résoudre ce système, on peut procéder par méthode d'addition.
Alors, en additionnant membre à membre les équations $(1)\ $ et $\ (2)$, on obtient :
$$\dfrac{2}{x}-\dfrac{1}{y}+\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{3}{5}+\dfrac{7}{5}$$
Cela donne : $\dfrac{3}{x}=\dfrac{10}{5}=2$
Donc, $2x=3$
Ce qui entraine : $\boxed{x=\dfrac{3}{2}}$
Ainsi, dans l'équation $(2)$, en remplaçant $x$ par $\dfrac{3}{2}$, on obtient :
$$\dfrac{1}{\dfrac{3}{2}}+\dfrac{1}{y}=\dfrac{7}{5}$$
C'est-à-dire ;
$$\dfrac{2}{3}+\dfrac{1}{y}=\dfrac{7}{5}$$
En résolvant cette équation, on trouve :
$\begin{array}{rcl} \dfrac{2}{3}+\dfrac{1}{y}=\dfrac{7}{5}&\Leftrightarrow&\dfrac{1}{y}=\dfrac{7}{5}-\dfrac{2}{3}\\\\&\Leftrightarrow&\dfrac{1}{y}=\dfrac{21}{15}-\dfrac{10}{15}\\\\&\Leftrightarrow&\dfrac{1}{y}=\dfrac{21-10}{15}\\\\&\Leftrightarrow&\dfrac{1}{y}=\dfrac{11}{15}\\\\&\Leftrightarrow&11y=15\\\\&\Leftrightarrow&y=\dfrac{15}{11}\end{array}$
Donc, $\boxed{y=\dfrac{15}{11}}$
Par conséquent, le système d'équations : $\left\lbrace\begin{array}{rcl}\dfrac{2}{x}-\dfrac{1}{y}&=&\dfrac{3}{5}\\ \\ \dfrac{1}{x}+\dfrac{1}{y}&=&\dfrac{7}{5}\end{array}\right.$ a pour solution dans $\mathbb{R}^{*}\times\mathbb{R}^{*}\ :$
$$S=\left\{\left(\dfrac{3}{2}\;;\ \dfrac{15}{11}\right)\right\}$$
3) Soit le système suivant :
$$\left\lbrace\begin{array}{rr} \dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{5}&\qquad(1)\\ \\ x+y+z=30&\qquad(2)\end{array}\right.$$
En considérant l'équation $(1)$, on a :
$$\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{5}\ \Leftrightarrow\ \dfrac{x}{2}=\dfrac{x+y+z}{2+3+5}$$
Or, d'après l'équation $(2)$, on a : $x+y+z=30$
Donc, en remplaçant $x+y+z$ par $30$, on obtient :
$$\dfrac{x}{2}=\dfrac{30}{2+3+5}=\dfrac{30}{10}$$
Ce qui donne : $\dfrac{x}{2}=3$
Ainsi, $\boxed{x=6}$
Alors, dans l'équation $(1)$, en remplaçant $x$ par $6$, on trouve :
$$\dfrac{6}{2}=\dfrac{y}{3}$$
Cela donne : $y=\dfrac{3\times 6}{2}=\dfrac{18}{2}=9$
Donc, $\boxed{y=9}$
Enfin, dans l'équation $(2)$, en remplaçant $x\ $ et $\ y$ par leur valeur, on obtient :
$$6+9+z=30$$
Ce qui entraine : $z=30-6-9=15$
Ainsi, $\boxed{z=15}$
Par conséquent, le système d'équations : $\left\lbrace\begin{array}{r} \dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{5}\\ \\ x+y+z=30\end{array}\right.$ a pour solution dans $\mathbb{R}\times\mathbb{R}\times\mathbb{R}\ :$
$$S=\left\{\left(6\;;\ 9\;;\ 15\right)\right\}$$
Exercice 9
On donne le système :
$$\left\lbrace\begin{array}{rclr} x^{2}+y^{2}&=&85&\qquad(1)\\\\xy&=&42&\qquad(2)\end{array}\right.$$
1) Calculons $(x+y)^{2}$
En utilisant la forme développée des identités remarquables, on a :
$$(x+y)^{2}=x^{2}+2\times xy+y^{2}$$
Ce peut encore s'écrire : $x^{2}+y^{2}+2\times xy$
Or, d'après les équations du système, on a : $x^{2}+y^{2}=85\ $ et $\ xy=42$
Donc, en remplaçant, on trouve :
$\begin{array}{rcl} x^{2}+y^{2}+2\times xy&=&85+2\times 42\\\\&=&85+84\\\\&=&169\end{array}$
Ainsi, $\boxed{(x+y)^{2}=169}$
2) Calculons $(x-y)^{2}$
En utilisant la forme développée des identités remarquables, on a :
$$(x-y)^{2}=x^{2}-2\times xy+y^{2}$$
Ce qui est équivalent à : $x^{2}+y^{2}+2\times xy$
Or, d'après les équations du système, on a : $x^{2}+y^{2}=85\ $ et $\ xy=42$
Donc, en remplaçant, on trouve :
$\begin{array}{rcl} x^{2}+y^{2}-2\times xy&=&85-2\times 42\\\\&=&85-84\\\\&=&1\end{array}$
D'où, $\boxed{(x-y)^{2}=1}$
3) Des questions précédentes, résolvons le système donné.
En effet, nous remarquons que :
En multipliant l'équation $(2)$ par $2$ et en ajoutant l'équation $(1)$, on trouve :
$$(x+y)^{2}=169$$
en multipliant l'équation $(2)$ par $-2$ et en ajoutant l'équation $(1)$, on trouve :
$$(x-y)^{2}=1$$
Donc, le système d'équations $\left\lbrace\begin{array}{rcl} x^{2}+y^{2}&=&85\\\\xy&=&42\end{array}\right.$ est équivalent au système
$$\left\lbrace\begin{array}{rclr} (x+y)^{2}&=&169&\qquad(3)\\\\(x-y)^{2}&=&1&\qquad(4)\end{array}\right.$$
Or, on a :
$(x+y)^{2}=169$ si, et seulement si, $\sqrt{(x+y)^{2}}=\sqrt{169}$
C'est-à-dire ; $|x+y|=13$
Ce qui donne : $x+y=13\ $ ou $\ x+y=-13$
$(x-y)^{2}=1$ si, et seulement si, $\sqrt{(x-y)^{2}}=\sqrt{1}$
Cela entraine : $|x-y|=1$
Ce qui donne : $x-y=1\ $ ou $\ x-y=-1$
Donc,
$-\ $ pour $x+y=13\ $ et $\ x-y=1$, on a le système suivant :
$$\left\lbrace\begin{array}{rclr} x+y&=&13&\qquad(5)\\\\x-y&=&1&\qquad(6)\end{array}\right.$$
En additionnant membre à membre les équations $(5)\ $ et $\ (6)$, on trouve :
$$x+y+x-y=13+1=14$$
Cela donne : $2x=14$
Ce qui entraine : $x=\dfrac{14}{2}=7$
D'où, $\boxed{x=7}$
En remplaçant $x$ par $7$, dans l'équation $(5)$, on obtient :
$$7+y=13$$
C'est-à-dire ; $y=13-7=6$
Donc, $\boxed{y=6}$
Ainsi, le couple $(7\;;\ 6)$ est solution du système donné.
$-\ $ pour $x+y=13\ $ et $\ x-y=-1$, on a le système suivant :
$$\left\lbrace\begin{array}{rclr} x+y&=&13&\qquad(7)\\\\x-y&=&-1&\qquad(8)\end{array}\right.$$
En additionnant membre à membre les équations $(7)\ $ et $\ (8)$, on trouve :
$$x+y+x-y=13-1=12$$
Cela donne : $2x=12$
Ce qui entraine : $x=\dfrac{12}{2}=6$
D'où, $\boxed{x=6}$
En remplaçant $x$ par $6$, dans l'équation $(7)$, on obtient :
$$6+y=13$$
C'est-à-dire ; $y=13-6=7$
Donc, $\boxed{y=7}$
Ainsi, le couple $(6\;;\ 7)$ est solution du système donné.
$-\ $ pour $x+y=-13\ $ et $\ x-y=1$, on a le système suivant :
$$\left\lbrace\begin{array}{rclr} x+y&=&-13&\qquad(9)\\\\x-y&=&1&\qquad(10)\end{array}\right.$$
En additionnant membre à membre les équations $(9)\ $ et $\ (10)$, on trouve :
$$x+y+x-y=-13+1=-12$$
Cela donne : $2x=-12$
Ce qui entraine : $x=\dfrac{-12}{2}=-6$
D'où, $\boxed{x=-6}$
En remplaçant $x$ par $-6$, dans l'équation $(9)$, on obtient :
$$-6+y=-13$$
C'est-à-dire ; $y=-13+6=-7$
Donc, $\boxed{y=-7}$
Ainsi, le couple $(-6\;;\ -7)$ est solution du système donné.
$-\ $ pour $x+y=-13\ $ et $\ x-y=-1$, on a le système suivant :
$$\left\lbrace\begin{array}{rclr} x+y&=&-13&\qquad(11)\\\\x-y&=&-1&\qquad(12)\end{array}\right.$$
En additionnant membre à membre les équations $(11)\ $ et $\ (12)$, on trouve :
$$x+y+x-y=-13-1=-14$$
Cela donne : $2x=-14$
Ce qui entraine : $x=\dfrac{-14}{2}=-7$
D'où, $\boxed{x=-7}$
En remplaçant $x$ par $-7$, dans l'équation $(11)$, on obtient :
$$-7+y=-13$$
C'est-à-dire ; $y=-13+7=-6$
Donc, $\boxed{y=-6}$
Ainsi, le couple $(-7\;;\ -6)$ est solution du système donné.
Par conséquent, le système d'équations : $\left\lbrace\begin{array}{rcl} x^{2}+y^{2}&=&85\\\\xy&=&42\end{array}\right.$ a pour solution dans $\mathbb{R}\times\mathbb{R}\ :$
$$S=\left\{\left(7\;;\ 6\right)\;,\ \left(6\;;\ 7\right)\;,\ \left(-6\;;\ -7\right)\;,\ \left(-7\;;\ -6\right)\right\}$$
Exercice 10
Nous allons procéder par une mise en équation.
Soit $x$ la longueur du terrain et $y$ la largeur.
Alors,
$-\ $ le périmètre est égal à : $2(x+y)$
$-\ $ l'aire est donnée par : $xy$
$-\ $ l'aire augmentée de $120\;m^{2}$ peut s'écrire : $xy+120$
$-\ $ la largeur augmentée de $5\;m$ devient : $(y+5)$
$-\ $ la longueur diminuée de $5\;m$ devient : $(x-5)$
$-\ $ avec ces nouvelles dimensions, l'aire devient : $(x-5)(y+5)$
Par hypothèse, ce terrain rectangulaire a un périmètre de $150\;m.$
Ce qui se traduit par : $2(x+y)=150$ ; équation (1)
Aussi, l'aire avec les nouvelles dimensions est égale à l'aire de départ augmentée de $120\;m^{2}.$
Cela peut s'écrire ainsi : $(x-5)(y+5)=xy+120$ équation (2)
Soit maintenant le système d'équations suivant : $$\left\lbrace\begin{array}{rcl} 2(x+y)&=&150\ \qquad\qquad(1)\\ (x-5)(y+5)&=&xy+120 \qquad(2)\end{array}\right.$$
Ce système est équivalent à : $$\left\lbrace\begin{array}{lcl} x+y&=&75\qquad(3)\\ x-y&=&29 \qquad(4)\end{array}\right.$$
En additionnant les équations (3) et (4) on obtient :
$x+y+x-y=75+29$
Donc, $2x=104$ ; d'où $x=52$
En remplaçant cette valeur de $x$ dans l'équation (3) on obtient :
$52+y=75$ ; c'est-à-dire $y=75-52=23$
Ainsi, ce terrain rectangulaire a pour longueur $52\;m$ et pour largeur $23\;m.$
Exercice 11
1) Mettons ce problème sous la forme d'un système d'équations du premier degré.
Soit $x$ les économies de Assane et $y$ celles de Ousseynou.
Par hypothèse, les économies de Ousseynou représentent les $4/5$ de celles de Assane.
Cela se traduit donc par : $y=\dfrac{4}{5}x$ ; équation (1)
Aussi, en réunissant leurs économies, il leur manque $2\,720$ francs pour effectuer leur achat. Ce qui veut dire qu'en ajoutant $2\,720$ francs à leurs économies, ils pourront acheter le magnétophone.
Cela se traduit alors par : $x+y+2\,720=20\,000$ ; équation (2)
On obtient le système d'équations suivant constitué des équations (1) et (2) : $$\left\lbrace\begin{array}{rcl} y&=&\dfrac{4}{5}x\\ \\x+y+2720&=&20000\end{array}\right.$$
2) Calculons alors le montant des économies de chacun des deux garçons.
Cela revient tout simplement à résoudre le système de la question 1).
On a : $$\left\lbrace\begin{array}{rcl} y&=&\dfrac{4}{5}x\quad\qquad(1)\\ \\x+y+2720&=&20000\qquad(2)\end{array}\right.$$
Remplaçons l'expression de $y$ dans l'équation (2).
On a alors : $x+\dfrac{4}{5}x+2\,720=20\,000$
donc, $\dfrac{9}{5}x=17\,280$ ; soit $x=\dfrac{17\,280\times 5}{9}=9\,600$
En remplaçant cette valeur de $x$ dans l'équation (1) on obtient :
$y=\dfrac{4\times 9\,600}{5}=7\,680$
Ainsi, les économies de Assane s'élèvent à $9\,600$ francs et celles de Ousseynou à $7\,680$ francs.
Exercice 12
Soit $x$ le nombre de garçons et $y$ le nombre de filles.
On sait qu'au début, il y a deux fois plus de garçons que de filles.
Cela se traduit donc par : $x=2y$ ; équation (1)
Lorsque six garçons quittent la salle le nombre de garçon devient alors : $(x-6)$
De même, lorsque six filles arrivent dans la salle le nombre de filles devient alors : $(y+6)$
A ce stade, on sait qu'il y a alors deux fois plus de filles que de garçons.
Ce qui peut se traduire par : $(y+6)=2(x-6)$
Cela est encore équivalent à $y=2x-18$ ; équation (2)
On obtient donc, le système suivant : $$\left\lbrace\begin{array}{rcl} x&=&2y\ \qquad\qquad(1)\\ y&=&2x-18\qquad(2)\end{array}\right.$$
En résolvant ce système, on trouvera le nombre de filles et de garçons de cette classe.
Prenons l'expression de $x$ dans l'équation (1) et remplaçons la dans l'équation (2).
On obtient alors : $y=2\times 2y-18$
Donc, $3y=18$ ; soit alors $y=\dfrac{18}{3}=6$
Remplaçons cette valeur de $y$ dans l'équation (1).
On obtient alors : $x=2\times 6=12$
Ainsi, cette classe comptait au début douze garçons et six filles.
Exercice 13
1) Résolvons le système suivant :
$$\left\lbrace\begin{array}{rclr} x+y&=&8&\qquad(1)\\\\x+2y&=&11&\qquad(2)\end{array}\right.$$
Pour cela, nous utilisons la méthode d'addition.
Multiplions d'abord l'équation $(1)$ par $-1.$
On obtient alors :
$$\left\lbrace\begin{array}{rclr} -x-y&=&-8&\qquad(3)\\\\x+2y&=&11&\qquad(2)\end{array}\right.$$
Additionnons ensuite membre à membre les équations $(3)\ $ et $\ (2).$
On trouve : $-x-y+x+2y=-8+11$
Cela donne : $\boxed{y=3}$
Enfin, en remplaçant cette valeur de $y$, dans l'équation $(2)$, on trouve :
$$x+2\times 3=11$$
C'est-à-dire ; $x+6=11$
Ce qui donne : $x=11-6=5$
Donc, $\boxed{x=5}$
Ainsi, le système $\left\lbrace\begin{array}{rcl} x+y&=&8\\\\x+2y&=&11\end{array}\right.$ a pour solution dans $\mathbb{R}\times\mathbb{R}\ :$
$$S=\left\{\left(5\;;\ 3\right)\right\}$$
2) On désigne par $x$ la longueur d'un rectangle et par $y$ sa largeur, exprimées en $cm.$ Le périmètre de ce rectangle est $16\;cm.$ Si l'on ajoute $3\;cm$ à la longueur et si l'on double la largeur le périmètre devient $28\;cm.$
Écrivons les deux équations correspondant à ces données.
En effet, comme $x$ est la longueur de ce rectangle et $y$ sa largeur alors, son périmètre est donné par : $2(x+y)$
Or, on sait que le périmètre de ce rectangle est égal à $16\;cm.$
Cela se traduit alors par : $2(x+y)=16$
Ce qui donne :
$$x+y=8\qquad(\text{équation 1})$$
Par ailleurs,
$-\ $ en ajoutant $3\;cm$ à la longueur, on obtient alors : $(x+3)$
$-\ $ en doublant la largeur, on obtient : $2y$
Alors, en considérant ces nouvelles dimensions, le périmètre devient : $2[(x+3)+2y]$
Or, avec ces dimensions, le périmètre est de $28\;cm.$
Cela se traduit alors par : $2[(x+3)+2y]=28$
Ce qui donne : $x+3+2y=14$
Ce qui entraine : $x+2y=14-3=11$
Ainsi,
$$x+2y=11\qquad(\text{équation 2})$$
3) Déterminons la longueur et la largeur de ce rectangle.
Pour déterminer la longueur et la largeur de ce rectangle, on va résoudre le système d'équations formé des équations $(1)\ $ et $\ (2).$
Soit alors le système suivant :
$$\left\lbrace\begin{array}{rcl} x+y&=&8\\\\x+2y&=&11\end{array}\right.$$
D'après les résultats de la question $1)$, ce système a pour solution : $S=\left\{\left(5\;;\ 3\right)\right\}.$
Ce qui signifie que : $x=5\ $ et $\ y=3$
Par conséquent, la longueur de ce rectangle est égale à $5\;cm$ et sa largeur est égale à $3\;cm.$
Exercice 14
1) Résolvons dans $\mathbb{R}\times\mathbb{R}$ le système suivant :
$$\left\lbrace\begin{array}{rclr} x+2y&=&625&\qquad(1)\\\\6x+13y&=&3\,975&\qquad(2)\end{array}\right.$$
En multipliant l'équation $(1)$ par $-6$, le système devient :
$$\left\lbrace\begin{array}{rclr} -6x-12y&=&-3\,750&\qquad(3)\\\\6x+13y&=&3\,975&\qquad(2)\end{array}\right.$$
En additionnant membre à membre les équations $(3)\ $ et $\ (2)$, on trouve :
$$-6x-12y+6x+13y=-3\,750+3\,975$$
Cela donne : $\boxed{y=225}$
En remplaçant ensuite cette valeur de $y$ dans l'équation $(1)$, on trouve :
$$x+2\times 225=625$$
C'est-à-dire ; $x+450=625$
Ce qui donne : $x=625-450=175$
Ainsi, $\boxed{x=175}$
Par conséquent, le système $\left\lbrace\begin{array}{rcl} x+2y&=&625\\\\6x+13y&=&3\,975\end{array}\right.$ a pour solution dans $\mathbb{R}\times\mathbb{R}\ :$
$$S=\left\{\left(175\;;\ 225\right)\right\}$$
2) Tante Adja dit à sa fille : "Avec $6\,250$ francs CFA j'achetais $10\;kg$ de pommes de terre et $20\;kg$ d'oignons. Après la dévaluation du franc CFA, je dois payer $7\,950$ francs CFA pour avoir les mêmes quantités".
Trouvons le prix d'un kilogramme de pommes de terre et celui d'oignons avant la dévaluation sachant que ces prix ont été multipliés respectivement par $1.2\ $ et $\ 1.3$ après la dévaluation
Soit :
$x$ le prix d'un kilogramme de pommes de terre avant la dévaluation
$y$ le prix d'un kilogramme d'oignons avant la dévaluation
Alors,
$-\ $ le prix de $10\;kg$ de pommes de terre est égal à : $10x$
$-\ $ le prix de $20\;kg$ d'oignons est égal à : $20y$
Comme Tante Adja a payé $6\,250$ francs CFA pour acheter $10\;kg$ de pommes de terre et $20\;kg$ d'oignons alors, cela se traduit par : $10x+20y=6\,250$
En divisant chaque membre de cette équation par $10$, on obtient :
$$x+2y=625\qquad(\text{équation 1})$$
Par ailleurs, après la dévaluation :
$-\ $ le prix d'un kilogramme de pommes de terre a été multiplié par $1.2$, ce prix devient alors : $1.2x$
$-\ $ le prix d'un kilogramme d'oignons a été multiplié par $1.3$, ce qui donne alors : $1.3y$
Avec ces nouveaux prix, Tante Adja doit payer $7\,950$ francs CFA pour $10\;kg$ de pommes de terre et $20\;kg$ d'oignons.
Cela se traduit alors par : $10\times 1.2x+20\times 1.3y=7\,950$
Ce qui donne : $12x+26y=7\,950$
Ainsi, en divisant chaque membre de cette équation par $2$, on obtient :
$$6x+13y=3\,975\qquad(\text{équation 2})$$
Pour trouver le prix d'un kilogramme de pommes de terre et celui d'oignons avant la dévaluation on va résoudre le système d'équations formé des équations $(1)\ $ et $\ (2).$
Soit alors à résoudre le système suivant :
$$\left\lbrace\begin{array}{rcl} x+2y&=&625\\\\6x+13y&=&3\,975\end{array}\right.$$
D'après les résultats de la question $1)$, ce système a pour solution : $S=\left\{\left(175\;;\ 225\right)\right\}.$
Ce qui signifie que : $x=175\ $ et $\ y=225$
Par conséquent, avant la dévaluation, le prix d'un kilogramme de pommes de terre était égal à $175\;F$ CFA et celui d'oignons avant la dévaluation était de $225\;F$ CFA.
Exercice 15
Les économies de Amy et Aly sont composées exclusivement de pièces de $250$ francs.
Amy dit à Aly : "Si tu me donnes six pièces, je disposerai alors de deux fois plus d'argent que toi ; mais si je donne quatre pièces, nous aurons les mêmes sommes d'argent".
1) En prenant $x\ $ et $\ y$ comme économies respectives de Amy et Aly, mettons ce problème sous la forme d'un système d'équations à deux inconnues.
En effet,
six pièces de $250\;F$ sont égales à : $6\times 250=1\,500\;F$
quatre pièces de $250\;F$ sont égales à : $4\times 250=1\,000\;F$
Donc,
$-\ $ si Aly donne six pièces en plus à Amy alors,
les économies de Amy deviennent : $x+1\,500$
les économies de Aly deviennent : $y-1\,500$
Comme dans ce cas les économies de Amy seront le double de celles de Aly alors, cela se traduit par : $x+1\,500=2(y-1\,500)$
Ce qui donne : $x+1\,500=2y-3\,000$
On obtient alors :
$$x+4\,500=2y\qquad(\text{équation 1})$$
$-\ $ si Aly donne quatre pièces en plus à Amy alors,
les économies de Amy deviennent : $x+1\,000$
les économies de Aly deviennent : $y-1\,000$
Comme dans ce cas les économies de Amy et celles de Aly seront les mêmes alors, cela se traduit par : $x+1\,000=y-1\,000$
Cela donne alors :
$$x+2\,000=y\qquad(\text{équation 2})$$
On obtient alors le système d'équations suivant, formé des équations $(1)\ $ et $\ (2)\ :$
$$\left\lbrace\begin{array}{rcl} x+4\,500&=&2y\\\\x+2\,000&=&y\end{array}\right.$$
2) Calculons le montant des économies de chacun.
Pour cela, nous allons résoudre le système d'équations trouvé à la question $1).$
Soit alors à résoudre le système suivant :
$$\left\lbrace\begin{array}{rcl} x+4\,500&=&2y\\\\x+2\,000&=&y\end{array}\right.$$
En multipliant chaque membre de la deuxième équation par $-1$, le système devient :
$$\left\lbrace\begin{array}{rcl} x+4\,500&=&2y\\\\-x-2\,000&=&-y\end{array}\right.$$
Alors, en additionnant ensuite membre à membre les deux équations de ce nouveau système, on trouve :
$$x+4\,500-x-2\,000=2y-y$$
Ce qui donne : $\boxed{y=2\,500}$
Enfin, en remplaçant cette valeur de $y$ dans première équation du système, on obtient :
$$x+4\,500=2\times 2\,500$$
Cela donne alors : $x+4\,000=5\,000$
Donc, $x=5\,000-4\,500=500$
D'où, $\boxed{x=500}$
Ainsi, les économies de Amy s'élèvent à $500\;F$ et celles de Aly s'élèvent à $1\,500\;F$
Exercice 16
J'ai deux fois l'âge que vous aviez quand j'avais l'âge que vous avez.
Et quand vous aurez mon âge, nous aurons à nous deux $63$ ans.
Déterminons nos âges.
Pour cela, nous allons mettre le problème sous forme de système d'équations à deux inconnues.
Soit $x$ mon âge et $y$ votre âge.
La différence des âges est donc égale à : $(x-y)$
$-\ $ Lorsque j'avais l'âge que vous avez,
mon âge était alors égal à : $x-(x-y)=x-x+y=y$
votre âge était alors égal à : $y-(x-y)=y-x+y=2y-x$
Dans ce cas, mon âge était le double de ton âge.
Cela se traduit par : $y=2(2y-x)=4y-2x$
Ce qui donne :
$$2x=3y\qquad(\text{équation 1})$$
$-\ $ Quand vous aurez mon âge,
votre âge serez alors égal à : $y+(x-y)=y+x-y=x$
mon âge sera alors égal à : $x+(x-y)=x+x-y=2x-y$
Dans ce cas, la somme de nos âges sera égale à $63$ ans.
Cela se traduit par : $x+2x-y=63$
Donc,
$$3x-y=63\qquad(\text{équation 2})$$
On obtient alors le système d'équations suivant, formé des équations $(1)\ $ et $\ (2)\ :$
$$\left\lbrace\begin{array}{rcl} 2x&=&3y\\\\3x-y&=&63\end{array}\right.$$
Pour déterminer nos âges, nous résolvons le système ci-dessus.
En considérant la première équation du système, on a : $x=\dfrac{3y}{2}$
En remplaçant cette expression de $x$ dans la deuxième équation, on obtient :
$$3\times\dfrac{3y}{2}-y=63$$
En résolvant cette équation, on trouve :
$\begin{array}{rcl} 3\times\dfrac{3y}{2}-y=63&\Rightarrow&\dfrac{9y}{2}-y=63\\\\&\Rightarrow&\dfrac{9y}{2}-\dfrac{2y}{2}=63\\\\&\Rightarrow&\dfrac{9y-2y}{2}=63\\\\&\Rightarrow&\dfrac{7y}{2}=63\\\\&\Rightarrow&7y=2\times 63\\\\&\Rightarrow&y=\dfrac{126}{7}\\\\&\Rightarrow&y=18\end{array}$
Donc, $\boxed{y=18}$
En remplaçant ensuite cette valeur de $y$ dans l'équation $x=\dfrac{3y}{2}$, on trouve :
$$x=\dfrac{3\times 18}{2}=\dfrac{54}{2}=27$$
Ce qui donne : $\boxed{x=27}$
Par conséquent, j'ai $27$ ans et vous en avez $18.$
Exercice 17
Le périmètre d'un triangle $ABC$ est égal à $120\;m.$ Les côtés sont respectivement proportionnels à $3\;,\ 4\ $ et $\ 5.$
Déterminons les dimensions de ce triangle.
Soit $x\;,\ y\ $ et $\ z$ les dimensions de ce triangle tels que : $AB=x\;,\ AC=y\ $ et $\ BC=z.$
Les côtés sont respectivement proportionnels à $3\;,\ 4\ $ et $\ 5$ avec un même coefficient de proportionnalité.
Cela signifie :
$$\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}\qquad(\text{équation 1})$$
Par ailleurs, le périmètre du triangle $ABC$ est égal à $120\;m.$
Ce qui se traduit par :
$$x+y+z=120\qquad(\text{équation 2})$$
On obtient alors le système d'équations suivant, formé des équations $(1)\ $ et $\ (2)\ :$
$$\left\lbrace\begin{array}{c} \dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}\\\\x+y+z=120\end{array}\right.$$
Alors, pour trouver les dimensions de ce triangle, nous résolvons le système ci-dessus.
En considérant l'équation $(1)$, on a :
$$\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}\ \Leftrightarrow\ \dfrac{x}{3}=\dfrac{x+y+z}{3+4+5}$$
Or, d'après l'équation $(2)$, on a : $x+y+z=120$
Donc, en remplaçant $x+y+z$ par $120$, on obtient :
$$\dfrac{x}{3}=\dfrac{120}{3+4+5}=\dfrac{120}{12}$$
Ce qui donne : $\dfrac{x}{3}=10$
Ainsi, $\boxed{x=30}$
Alors, dans l'équation $(1)$, en remplaçant $x$ par $30$, on trouve :
$$\dfrac{30}{3}=\dfrac{y}{4}$$
Cela donne : $y=\dfrac{4\times 30}{3}=\dfrac{120}{3}=40$
Donc, $\boxed{y=40}$
Enfin, dans l'équation $(2)$, en remplaçant $x\ $ et $\ y$ par leur valeur, on obtient :
$$30+40+z=120$$
Ce qui entraine : $z=120-30-40=50$
Ainsi, $\boxed{z=50}$
Par conséquent, les dimensions du triangles $ABC$ son : $AB=30\;cm\;,\ AC=40\;cm\ $ et $\ BC=50\;cm.$
Exercice 18
Richard possède une certaine somme d'argent. Il envisage d'en dépenser les $2/3$ pour acheter un album de timbres, et d'en encaisser le quart en revendant ses timbres en double. Il lui restera alors $210$ francs
Déterminons la somme que Richard possède.
Soit $x$ la somme disposée par Richard.
Richard envisage de dépenser les $\dfrac{2}{3}$ de cette somme pour acheter un album de timbres.
$-\ $ Donc, la somme dépensée pour acheter un album de timbres est égale à : $\dfrac{2}{3}x$
En revendant ses timbres, Richard encaisse une somme équivalente au quart de la somme qu'il disposait.
$-\ $ Donc, la somme encaissée par Richard est égale à : $\dfrac{1}{4}x$
Enfin, il lui reste $210$ francs.
Ce qui peut se traduit par :
$$x-\dfrac{2}{3}x+\dfrac{1}{4}x=210$$
Alors, en résolvant cette équation, on trouve :
$\begin{array}{rcl} x-\dfrac{2}{3}x+\dfrac{1}{4}x=210&\Leftrightarrow&\dfrac{12}{12}x-\dfrac{8}{12}x+\dfrac{3}{12}x=210\\\\&\Leftrightarrow&\dfrac{12x-8x+3x}{12}=210\\\\&\Leftrightarrow&\dfrac{7x}{12}=210\\\\&\Leftrightarrow&7x=210\times 12\\\\&\Leftrightarrow&7x=2\,520\\\\&\Leftrightarrow&x=\dfrac{2\,520}{7}\\\\&\Leftrightarrow&x=360\end{array}$
Donc, $\boxed{x=360}$
Ainsi, Richard dispose d'une somme d'argent égale à : $360\;F$
Exercice 19
Un transporteur a livré $144$ caisses, toutes identiques, et $25$ fûts tous de même masse, en trois voyages. Le premier chargement de $56$ caisses et de $4$ fûts atteignait $3\,480\;kg.$
Le second de $40$ caisses et $7$ fûts pesait $4\,350\;kg.$
Déterminons la masse du dernier chargement.
En effet,
$-\ $ le nombre de caisses que compte le dernier chargement est égal à :
$$144-56-40=48$$
$-\ $ le nombre de fûts que compte le dernier chargement est égal à :
$$25-4-7=14$$
Donc, le dernier chargement est composé de $48$ caisses et de $14$ fûts.
Déterminons alors le poids d'une caisse et le poids d'un fût.
Pour cela, nous allons mettre le problème sous forme de système d'équations à deux inconnues.
Soit $x$ le poids d'une caisse et $y$ le poids d'un fût.
$-\ $ Le premier chargement compte $56$ caisses et $4$ fûts.
Alors, le poids du premier chargement est donné par : $56x+4y$
Or, ce premier chargement atteignait $3\,480\;kg.$
Donc, on a : $56x+4y=3\,480$
Alors, en divisant chaque membre de cette équation par $4$, on trouve :
$$14x+y=870\qquad(\text{équation 1})$$
$-\ $ Le second chargement compte $40$ caisses et $7$ fûts.
Donc, le poids de ce second chargement est donné par : $40x+7y$
Comme ce second chargement pesait $4\,350\;kg$ alors, cela se traduit par :
$$40x+7y=4\,350\qquad(\text{équation 2})$$
On obtient alors le système d'équations suivant, formé des équations $(1)\ $ et $\ (2)\ :$
$$\left\lbrace\begin{array}{rcl} 14x+y&=&870\\\\40x+7y&=&4\,350\end{array}\right.$$
Alors, pour trouver le poids d'une caisse et d'un fût, nous résolvons le système ci-dessus.
En multipliant l'équation $(1)$ par $-7$, on obtient le système suivant :
$$\left\lbrace\begin{array}{rclr} -98x-7y&=&-6\,090&\qquad(3)\\\\40x+7y&=&4\,350&\qquad(2)\end{array}\right.$$
En additionnant membre à membre les équations $(3)\ $ et $\ (2)$, on obtient :
$$-98x-7y+40x+7y=-6\,090+4\,350$$
Ce qui donne : $-58x=-1740$
Par suite, $x=\dfrac{-1740}{-58}=30$
Ainsi, $\boxed{x=30}$
En remplaçant cette valeur de $x$ dans l'équation $(1)$, on trouve :
$$14\times 30+y=870$$
Ce qui entraine : $y=870-420=450$
D'où, $\boxed{y=450}$
Par conséquent, chaque caisse pèse $30\;kg$ et chaque fût pèse $450\;kg$
Comme le dernier chargement compte $48$ caisses et $14$ fûts sa masse est donné par :
$$48\times 30+14\times 450=1\,440+6\,300=7\,740$$
Ainsi, le dernier chargement pèse $7\,740\;kg.$
Exercice 20
Un âne porte $15$ sacs de sel et $2\;kg$ d'olives. Un mulet porte $2$ sacs de sel et $41\;kg$ d'olives. L'âne souffle fort! "De quoi te plains-tu ?" dit le mulet, "nous portons la même charge"
Déterminons la masse, en kilogramme, d'un sac de sel.
Soit $x$ le poids d'un sac de sel.
Alors,
$-\ $ la masse totale portée par l'âne est égale à : $15x+2$
$-\ $ la masse totale portée par le mulet est égale à : $2x+41$
Comme l'âne et le mulet portent la même charge alors, cela se traduit par :
$$15x+2=2x+41$$
En résolvant cette équation, on obtient :
$\begin{array}{rcl} 15x+2=2x+41&\Leftrightarrow&15x-2x=41-2\\\\&\Leftrightarrow&13x=39\\\\&\Leftrightarrow&x=\dfrac{39}{13}\\\\&\Leftrightarrow&x=3\end{array}$
Donc, $\boxed{x=3}$
Donc, le poids d'un sac de sel est de $3\;kg.$
Exercice 21
Une ficelle de $70\;cm$ est fixée à deux clous $A\ $ et $\ B$ distants de $20\;cm.$ On tend la ficelle jusqu'à un point $C$ tel que $ABC$ est un triangle rectangle en $A.$
Calculons alors les longueurs $AC\ $ et $\ BC.$
Pour cela, nous allons mettre ce problème sous de système d'équations à deux inconnues.
Soit $x$ la longueur $AC\ $ et $\ y$ la longueur $BC.$
Alors, le périmètre du triangle $ABC$ est donné par :
$$AB+AC+BC=20+x+y$$
Comme la ficelle mesure $70\;cm$ alors, cela signifie que le périmètre du triangle $ABC$ est égal à $70\;cm.$
Ce qui se traduit par : $20+x+y=70$
Ce qui entraine : $x+y=70-20$
Cela donne alors :
$$x+y=50\qquad(\text{équation 1})$$
Par ailleurs, le triangle $ABC$ est rectangle en $A.$
Donc, en utilisant le théorème de Pythagore, on a :
$$BC^{2}=AB^{2}+AC^{2}$$
C'est-à-dire ; $y^{2}=(20)^{2}+x^{2}$
Cela donne alors :
$$y^{2}-x^{2}=400\qquad(\text{équation 2})$$
On obtient alors le système d'équations suivant, formé des équations $(1)\ $ et $\ (2)\ :$
$$\left\lbrace\begin{array}{rcl} x+y&=&50\\\\y^{2}-x^{2}&=&400\end{array}\right.$$
En remarquant que $y^{2}-x^{2}=(y-x)(y+x)$, ce système peut encore s'écrire :
$$\left\lbrace\begin{array}{rclr} x+y&=&50&\qquad(1)\\\\(y-x)(x+y)&=&400&\qquad(2)\end{array}\right.$$
Résolvons alors le système ci-dessus
En effet, dans l'équation $(2)$, en remplaçant $(x+y)$ par $50$, on obtient :
$$\left\lbrace\begin{array}{rclr} x+y&=&50&\qquad(1)\\\\(y-x)\times 50&=&400&\qquad(3)\end{array}\right.$$
Ce qui est équivalent à :
$$\left\lbrace\begin{array}{rclr} x+y&=&50&\qquad(1)\\\\y-x&=&\dfrac{400}{50}=8&\qquad(3)\end{array}\right.$$
En additionnant membre à membre les équations $(1)\ $ et $\ (3)$, on trouve :
$$x+y+y-x=50+8$$
Ce qui donne : $2y=58$
D'où, $\boxed{y=29}$
En remplaçant cette valeur de $y$ dans l'équation $(1)$, on obtient :
$$x+29=50$$
Cela donne : $x=50-29=21$
Donc, $\boxed{x=21}$
Par conséquent, les dimensions du triangle $ABC$ sont : $AB=20\;cm\;,\ AC=21\;cm\ $ et $\ BC=29\;cm.$
Exercice 22
La moyenne de six notes est $4.$ On ajoute une note et la moyenne devient $5.$
Déterminons cette septième note.
Soit $y$ la somme des six notes et $x$ la septième note.
Alors, la moyenne de ces six notes est donnée par : $\dfrac{y}{6}$
Comme la moyenne des six notes est égale à $4$ alors, cela se traduit par :
$$\dfrac{y}{6}=4\qquad(\text{équation 1})$$
En ajoutant une septième note aux six premières, la moyenne devient : $\dfrac{y+x}{7}$
Or, cette moyenne est égale à $5.$
Ce qui signifie que :
$$\dfrac{y+x}{7}=5\qquad(\text{équation 2})$$
Soit alors le système d'équations suivant, formé des équations $(1)\ $ et $\ (2)\ :$
$$\left\lbrace\begin{array}{rcl} \dfrac{y}{6}&=&4\\\\\dfrac{y+x}{7}&=&5\end{array}\right.$$
En considérant l'équation $(1)$, on a : $\dfrac{y}{6}=4$
Ce qui entraine : $y=4\times 6=24$
D'où, $\boxed{y=24}$
En remplaçant cette valeur de $y$ dans l'équation $(2)$, on trouve :
$$\dfrac{24+x}{7}=5$$
Ce qui donne : $24+x=5\times 7=35$
C'est-à-dire ; $x=35-24=11$
Donc, $\boxed{x=11}$
Par conséquent, cette septième note est égale à $11.$
Exercice 23
Trouvons trois nombres entiers naturels consécutifs dont la somme vaut $1\,995.$
Soit $x\;,\ y\ $ et $\ z$ trois nombres entiers naturels consécutifs.
Donc :
$y$ est le nombre entier naturel qui suit consécutivement l'entier $x$, ce qui peut s'écrire :
$$y=x+1$$
$z$ est le nombre entier naturel qui vient juste après $y.$ Ce qui se traduit par :
$$z=y+1$$
En remplaçant $y$ par son expression, on trouve : $z=x+1+1=x+2$
Comme la somme de ces trois nombres est égale à $1\,993$ alors, cela se traduit par :
$$x+y+z=1\,995$$
Dans cette équation, en remplaçant $y\ $ et $\ z$ par leur expression en fonction de $x$, on obtient :
$$x+x+1+x+2=1\,995$$
Ce qui donne : $3x+3=1\,995$
Ce qui entraine : $3x=1\,995-3$
Par suite, $x=\dfrac{1\,992}{3}=664$
Donc, $\boxed{x=664}$
En remplaçant cette valeur de $x$ dans l'expression de $y$, on trouve :
$$y=664+1=665$$
Donc, $\boxed{y=665}$
En remplaçant cette valeur de $y$ dans l'expression de $z$, on trouve :
$$y=665+1=666$$
Donc, $\boxed{z=666}$
Ainsi, les trois nombres entiers naturels consécutifs dont la somme vaut $1995$ sont :
$$664\;;\quad 665\;;\quad 666$$
Exercice 24
David et Fabrice ont respectivement $15$ ans et $5$ ans.
Déterminons le nombre d'années pendant lequel l'âge de David sera le double de celui de Fabrice.
Soit $x$ le nombre d'années pour lequel l'âge de David sera le double de celui de Fabrice.
Alors,
$-\ $ dans $x$ années, l'âge de David sera égale à : $15+x$
$-\ $ dans $x$ années, l'âge de Fabrice sera égale à : $5+x$
Or, à ce moment, l'âge de David sera le double de celui de Fabrice.
Cela se traduit alors par :
$$15+x=2(5+x)$$
En résolvant cette équation, on trouve :
$\begin{array}{rcl} 15+x=2(5+x)&\Leftrightarrow&15+x=10+2x\\\\&\Leftrightarrow&x-2x=10-15\\\\&\Leftrightarrow&-x=-5\\\\&\Leftrightarrow&x=5\end{array}$
Donc, $\boxed{x=5}$
Ce qui signifie que dans $5$ ans, l'âge de David sera le double de celui de Fabrice.
Déterminons le nombre d'années pour lequel l'âge de David sera le triple de celui de Fabrice.
En effet, en observant les âges de David et de Fabrice, nous constatons que l'âge de David est déjà le triple de celui de Fabrice.
$$15=3\times 5$$
Donc, au départ, l'âge de David est déjà le triple de celui de Fabrice.
Déterminons le nombre d'années pour lequel l'âge de David sera $6$ fois plus grand que celui de Fabrice.
Soit $x$ le nombre d'années pour lequel l'âge de David sera $6$ fois plus grand que celui de Fabrice.
Alors,
$-\ $ dans $x$ années, l'âge de David sera égale à : $15+x$
$-\ $ dans $x$ années, l'âge de Fabrice sera égale à : $5+x$
Comme l'âge de David est $6$ fois plus grand que celui de Fabrice alors, cela se traduit par :
$$15+x=6(5+x)$$
En résolvant cette équation, on trouve :
$\begin{array}{rcl} 15+x=6(5+x)&\Leftrightarrow&15+x=30+6x\\\\&\Leftrightarrow&x-6x=30-15\\\\&\Leftrightarrow&-5x=15\\\\&\Leftrightarrow&x=\dfrac{15}{-5}\\\\&\Leftrightarrow&x=-3\end{array}$
Donc, $\boxed{x=-3}$
Or, le nombre d'années doit être toujours positif.
Par conséquent, l'âge de David ne sera jamais $6$ fois plus grand que celui de Fabrice.
Par contre, $x=-3$ signifie que : il y a de cela $3$ ans, l'âge de David était $6$ fois plus grand que celui de Fabrice.
C'est-à-dire ; lorsque David avait $(15-3)=12$ ans et Fabrice $(5-3)=2$ ans.
On constate alors que : $12=6\times 2$
Exercice 25
Un père a $27$ ans de plus que son fils. Dans $6$ ans, son âge sera le double de celui de son fils.
Déterminons les âges du père et du fils.
Pour cela, nous allons mettre ce problème sous forme de système d'équations à deux inconnues.
Soit $x$ l'âge du père et $y$ l'âge du fils.
Comme le père a $27$ ans de plus que son fils alors, cela se traduit par :
$$x=y+27\qquad(\text{équation 1})$$
Dans $6$ ans :
$-\ $ l'âge du père sera égal à : $x+6$
$-\ $ l'âge du fils sera égal à : $y+6$
Comme dans ce cas l'âge du père sera le double de celui de son fils alors, cela se traduit par :
$$x+6=2(y+6)\qquad(\text{équation 2})$$
Nous obtenons alors le système d'équations suivant, formé des équations $(1)\ $ et $\ (2)\ :$
$$\left\lbrace\begin{array}{rcl} x&=&y+27\\\\x+6&=&2(y+6)\end{array}\right.$$
Dans l'équation $(2)$, en remplaçant $x$ par son expression, on trouve :
$$y+27+6=2(y+6)$$
En résolvant cette équation, on obtient :
$\begin{array}{rcl} y+27+6=2(y+6)&\Leftrightarrow&y+33=2y+12\\\\&\Leftrightarrow&y-2y=12-33\\\\&\Leftrightarrow&-y=-21\\\\&\Leftrightarrow&y=21\end{array}$
Donc, $\boxed{y=21}$
En remplaçant cette valeur de $y$ dans l'équation $(1)$, on trouve :
$$x=21+27=48$$
Donc, $\boxed{x=48}$
Par conséquent, le père a $48$ ans et son fils $21$ ans.
Exercice 26
Une mère de $37$ ans a trois enfants âgés de $8\;,\ 10\ $ et $\ 13$ ans.
Nous allons déterminer le nombre d'années au bout duquel l'âge de la mère sera égal à la somme des âges de ses enfants.
Pour cela, nous procédons par une mise en équation.
Soit $x$ le nombre d'années au bout duquel l'âge de la mère sera égal à la somme des âges de ses enfants.
Alors, au bout de $x$ années :
$-\ $ l'âge de la mère sera égal à : $37+x$
$-\ $ l'âge de l'enfant de $8$ ans sera égal à : $8+x$
$-\ $ l'âge de l'enfant de $10$ ans sera égal à : $10+x$
$-\ $ l'âge de l'enfant de $13$ ans sera égal à : $13+x$
Donc, au bout de $x$ années la somme des âges des trois enfants sera donnée par :
$$8+x+10+x+13+x=31+3x$$
De plus, on sait qu'au bout de $x$ années l'âge de la mère sera égal à la somme des âges de ses enfants.
Cette hypothèse se traduit par :
$$37+x=31+3x$$
En résolvant cette équation, on obtient :
$37+x=31+3x$ si, et seulement si, $37-31=3x-x$
Par suite, $6=2x$ soit encore $2x=6$
Ce qui donne : $x=\dfrac{6}{2}=3$
Ainsi, au bout de $3$ ans, l'âge de la mère sera égal à la somme des âges de ses enfants.
Exercice 27
Pierre dit à Yves : "J'ai $5$ fois l'âge que tu avais quand j'avais l'âge que tu as". Yves lui répond : "Quand tu auras l'âge que j'ai, la somme de nos âges sera $88$ ans"
Déterminons l'âge de Pierre.
Pour cela, nous allons mettre le problème sous forme de système d'équations à deux inconnues.
Soit $x$ l'âge Pierre et $y$ celui de Yves.
La différence de leurs âges est donc égale à : $(x-y)$
$-\ $ Lorsque Pierre avait l'âge de Yves alors,
l'âge de Pierre était égal à : $x-(x-y)=x-x+y=y$
l'âge de Yves était égal à : $y-(x-y)=y-x+y=2y-x$
Comme l'âge de Pierre était $5$ fois celui de Yves alors, cela se traduit par :
$$y=5(2y-x)=10y-5x$$
Ce qui est équivalent à :
$$9y-5x=0\qquad(\text{équation 1})$$
$-\ $ Quand Yves aura l'âge de Pierre alors,
l'âge de Yves sera égal à : $y+(x-y)=y+x-y=x$
l'âge de Pierre sera égal à : $x+(x-y)=x+x-y=2x-y$
Dans ce cas, la somme de leurs âges est égale à $88$ ans.
Cela se traduit par :
$$x+2x-y=88$$
Donc,
$$3x-y=88\qquad(\text{équation 2})$$
On obtient alors le système d'équations suivant, formé des équations $(1)\ $ et $\ (2)\ :$
$$\left\lbrace\begin{array}{rcl} 9y-5x&=&0\\\\3x-y&=&88\end{array}\right.$$
Pour déterminer leurs âges respectifs, nous résolvons le système ci-dessus.
En considérant la première équation du système, on a :
$9y-5x=0$ si, et seulement si, $5x=9y$
C'est-à-dire ; $x=\dfrac{9y}{5}$
En remplaçant cette expression de $x$ dans la deuxième équation, on obtient :
$$3\times\dfrac{9y}{5}-y=88$$
En résolvant cette équation, on trouve :
$\begin{array}{rcl} 3\times\dfrac{9y}{5}-y=88&\Leftrightarrow&\dfrac{27y}{5}-y=88\\\\&\Leftrightarrow&\dfrac{27y}{5}-\dfrac{5y}{5}=88\\\\&\Leftrightarrow&\dfrac{27y-5y}{5}=88\\\\&\Leftrightarrow&\dfrac{22y}{5}=88\\\\&\Leftrightarrow&22y=5\times 88\\\\&\Leftrightarrow&y=\dfrac{440}{22}\\\\&\Leftrightarrow&y=20\end{array}$
Donc, $\boxed{y=20}$
Or, d'après l'équation $(1)$, on a : $x=\dfrac{9y}{5}$
Donc, en remplaçant $y$ par sa valeur, on trouve :
$$x=\dfrac{9\times 20}{5}=\dfrac{180}{5}=36$$
Ce qui donne : $\boxed{x=36}$
Par conséquent, Pierre a $36$ ans et Yves a $20$ ans.
Exercice 28
Quand le père avait l'âge du fils, le fils avait $10$ ans.
Quand le fils aura l'âge du père, le père aura $70$ ans.
Déterminons leurs âges respectifs.
Soit $x$ l'âge du père et $y$ celui du fils.
La différence de leurs âges est donc égale à : $(x-y)$
$-\ $ Lorsque le père avait l'âge du fils alors,
l'âge du père était égal à : $x-(x-y)=x-x+y=y$
l'âge du fils était égal à : $y-(x-y)=y-x+y=2y-x$
Comme le fils avait $10$ ans à cette époque alors, cela peut s'écrire :
$$2y-x=10\qquad(\text{équation 1})$$
$-\ $ Quand le fils aura l'âge du père alors,
l'âge du fils sera égal à : $y+(x-y)=y+x-y=x$
l'âge du père sera égal à : $x+(x-y)=x+x-y=2x-y$
Comme à ce moment le père aura $70$ ans alors, cela se traduit par :
$$2x-y=70\qquad(\text{équation 2})$$
On obtient alors le système d'équations suivant, formé des équations $(1)\ $ et $\ (2)\ :$
$$\left\lbrace\begin{array}{rcl} 2y-x&=&10\\\\2x-y&=&70\end{array}\right.$$
Pour déterminer leurs âges respectifs, nous résolvons le système ci-dessus.
En multipliant chaque membre de l'équation $(1)$ par $2$, on obtient le système suivant :
$$\left\lbrace\begin{array}{rclr} 4y-2x&=&20&\qquad(3)\\\\2x-y&=&70&\qquad(2)\end{array}\right.$$
En additionnant membre à membre les équations $(3)\ $ et $\ (2)$, on trouve :
$$4y-2x+2x-y=20+70$$
Cela donne : $3y=90$
Ce qui entraine : $y=\dfrac{90}{3}=30$
Donc, $\boxed{y=30}$
En remplaçant cette valeur de $y$ dans la deuxième équation, on obtient :
$$2x-30=70$$
Donc, $2x=70+30=100$
Par suite, $x=\dfrac{100}{2}=50$
D'où, $\boxed{x=50}$
Par conséquent, l'âge du père est égal a $50$ ans et celui du fils est égal a $30$ ans.
Exercice 29
Si on augmente de $3$ mètres la longueur du côté d'un carré, l'aire augmente de $45\;m^{2}.$
Déterminons l'aire de ce carré.
Soit $x$ la longueur du côté de ce carré.
Alors,
$-\ $ l'aire est donnée par : $x^{2}$
$-\ $ l'aire augmentée de $45\;m^{2}$ peut s'écrire : $x^{2}+45$
En augmentant de $3\;m$ le côté alors,
$-\ $ la longueur du côté devient : $(x+3)$
$-\ $ avec ces nouvelles dimension, l'aire devient : $(x+3)^{2}$
Or, on sait que si on augmente de $3$ mètres la longueur du côté d'un carré, l'aire augmente de $45\;m^{2}.$
Cela signifie que l'aire avec les nouvelles est égale à l'aire augmentée de $45\;m^{2}.$
Ce qui se traduit alors par :
$$(x+3)^{2}=x^{2}+45$$
En résolvant cette équation, on trouve :
$\begin{array}{rcl} (x+3)^{2}=x^{2}+45&\Leftrightarrow&x^{2}+6x+9=x^{2}+45\\\\&\Leftrightarrow&x^{2}+6x-x^{2}=45-9\\\\&\Leftrightarrow&6x=36\\\\&\Leftrightarrow&x=\dfrac{36}{6}\\\\&\Leftrightarrow&x=6\end{array}$
Donc, $\boxed{x=6}$
Ainsi, la longueur du côté de ce carré est égale à $6\;m.$
Par conséquent, son aire est de : $6^{2}=36\;m^{2}.$
Exercice 30
Trouvons les nombre réels $a\ $ et $\ b$ tels que les couples $(-1\;;\ 3)\ $ et $\ (2\;;\ -5)$ soient solutions de l'équation $ax+by-1=0$
En effet, comme le couple $(-1\;;\ 3)$ est solution de l'équation $ax+by-1=0$ alors, en remplaçant $x$ par $-1\ $ et $\ y$ par $3$, on obtient :
$$-a+3b-1=0\qquad(\text{équation 1})$$
Aussi, comme le couple $(2\;;\ -5)$ est solution de l'équation $ax+by-1=0$ alors, remplaçons $x$ par $2\ $ et $\ y$ par $-5.$
On trouve :
$$2a-5b-1=0\qquad(\text{équation 2})$$
Considérons alors le système d'équations suivant, formé des équations $(1)\ $ et $\ (2)\ :$
$$\left\lbrace\begin{array}{rclr} -a+3b-1&=&0&\qquad(1)\\\\2a-5b-1&=&0&\qquad(2)\end{array}\right.$$
Pour déterminer les nombres réels $a\ $ et $\ b$, nous résolvons le système ci-dessus.
En multipliant chaque membre de l'équation $(1)$ par $2$, on obtient le système suivant :
$$\left\lbrace\begin{array}{rclr} -2a+6b-2&=&0&\qquad(3)\\\\2a-5b-1&=&0&\qquad(2)\end{array}\right.$$
En additionnant membre à membre les équations $(3)\ $ et $\ (2)$, on trouve :
$$-2a+6b-2+2a-5b-1=0$$
Cela donne : $b-3=0$
D'où, $\boxed{b=3}$
En remplaçant cette de $b$ dans l'équation $(2)$, on obtient :
$$2a-5\times 3-1=0$$
Alors, $2a-15-1=0$
Ce qui entraine : $2a=16$
Par suite, $a=\dfrac{16}{2}=8$
Donc, $\boxed{a=8}$
Exercice 31
1) Résolvons le système :
$$\left\lbrace\begin{array}{rclr} x+y&=&110&\qquad(1)\\ 2x+5y&=&340&\qquad(2)\end{array}\right.$$
En multipliant chaque membre de l'équation $(1)$ par $-2$, le système devient :
$$\left\lbrace\begin{array}{rclr} -2x-2y&=&-220&\qquad(3)\\\\2x+5y&=&340&\qquad(2)\end{array}\right.$$
En additionnant membre à membre les équations $(3)\ $ et $\ (2)$, on trouve :
$$-2x-2y+2x+5y=-220+340$$
Cela donne : $3y=120$
Donc, $y=\dfrac{120}{3}=40$
D'où, $\boxed{y=40}$
En remplaçant ensuite cette valeur de $y$ dans l'équation $(1)$, on trouve :
$$x+40=110$$
Ce qui donne : $x=110-40=70$
Ainsi, $\boxed{x=70}$
Par conséquent, le système $\left\lbrace\begin{array}{rcl} x+y&=&110\\\\2x+5y&=&340\end{array}\right.$ a pour solution dans $\mathbb{R}\times\mathbb{R}\ :$
$$S=\left\{\left(70\;;\ 40\right)\right\}$$
2) Un théâtre propose deux types de billets les uns à $1\,000\;F$ et les autres à $2\,500\;F.$
On sait que $110$ spectateurs ont assisté à cette représentation théâtrale et que la recette totale s'élève à $170\,000\;F.$
Calculons le nombre de billets vendus pour chaque type.
Soit :
$x$ le nombre de billets dont le prix est $1\,000\;F$ l'unité
$y$ le nombre de billets dont le prix est $2\,500\;F$ l'unité
Comme $110$ spectateurs ont assisté à cette représentation théâtrale alors, cela signifie que le nombre total de billets vendus est égal à $110.$
Cela peut donc s'écrire :
$$x+y=110\qquad(\text{équation 1})$$
Par ailleurs, on sait que la recette totale s'élève à $170\,000\;F.$
Cela se traduit par : $1\,000\times x+2\,500\times y=170\,000$
Ce qui donne : $1\,000x+2\,500y=170\,000$
Alors, en divisant chaque membre de cette équation par $500$, on obtient :
$$2x+5y=340\qquad(\text{équation 2})$$
Pour trouver le nombre de billets vendus pour chaque type, nous allons résoudre le système d'équations formé des équations $(1)\ $ et $\ (2).$
Soit alors à résoudre le système suivant :
$$\left\lbrace\begin{array}{rcl} x+y&=&110\\\\2x+5y&=&340\end{array}\right.$$
D'après les résultats de la question $1)$, ce système a pour solution : $S=\left\{\left(70\;;\ 40\right)\right\}.$
Ce qui signifie que : $x=70\ $ et $\ y=40$
Par conséquent, le théâtre a vendu $70$ billets de $1\,000\;F\ $ et $\ 40$ billets de $2\,500\;F.$
Auteur:
Diny Faye

Commentaires
pape (non vérifié)
jeu, 02/14/2019 - 22:20
Permalien
Bonne travail
pape (non vérifié)
jeu, 02/14/2019 - 22:22
Permalien
Bon travail
Aminata (non vérifié)
mar, 03/12/2019 - 15:06
Permalien
Ou sont les problemes
Aminata (non vérifié)
mar, 03/12/2019 - 15:08
Permalien
Ou sont les problemes
Anonyme (non vérifié)
mar, 04/16/2019 - 23:46
Permalien
Bon travail
Zeynab (non vérifié)
lun, 04/22/2019 - 20:57
Permalien
Il y a seulement les
Zeynab (non vérifié)
lun, 04/22/2019 - 20:57
Permalien
Il y a seulement les
fdini
lun, 04/22/2019 - 21:23
Permalien
T'inquiète zeynab on y est,
T'inquiète zeynab on y est, on va bientôt mettre le reste des corrigés
Anonyme (non vérifié)
ven, 05/17/2019 - 08:56
Permalien
Merci sunu daara on l'appelle
Mame Mor (non vérifié)
jeu, 01/16/2025 - 20:53
Permalien
Jaajëf
Gana (non vérifié)
dim, 11/24/2019 - 22:55
Permalien
Fantastique
David (non vérifié)
sam, 04/18/2020 - 00:28
Permalien
Apprendre
David (non vérifié)
sam, 04/18/2020 - 00:29
Permalien
Apprendre
David (non vérifié)
sam, 04/18/2020 - 00:30
Permalien
Apprendre
David (non vérifié)
sam, 04/18/2020 - 00:31
Permalien
Apprendre
David (non vérifié)
sam, 04/18/2020 - 00:31
Permalien
Apprendre
Anonyme (non vérifié)
lun, 05/18/2020 - 16:03
Permalien
Machallah merci beaucoup pour
Fatoumata diallo (non vérifié)
lun, 03/22/2021 - 10:10
Permalien
Très bon travail
Mourtalla (non vérifié)
dim, 04/18/2021 - 18:32
Permalien
La correction de 28
Kane (non vérifié)
dim, 03/06/2022 - 22:26
Permalien
Correction exo 36 svp
Khassim (non vérifié)
lun, 12/19/2022 - 23:40
Permalien
Correction exercice 25 s'il
Moussa Millimono (non vérifié)
jeu, 10/12/2023 - 03:45
Permalien
Révision
Doul (non vérifié)
mer, 03/19/2025 - 07:06
Permalien
Ha ah ah ah c'est trop cool
Ajouter un commentaire