Solution des exercices : Les forces - 3e
Classe:
Troisième
Exercice 1
1) Une intensité : c'est la valeur numérique exprimée en unité de force.
2) Une droite d'action : c'est la droite suivant laquelle la force agit ; elle peut être horizontale, oblique ou verticale.
3) On mesure la valeur d'une force à l'aide d'un dynamomètre.
Exercice 2
Représentons par un vecteur chacune des forces suivantes :
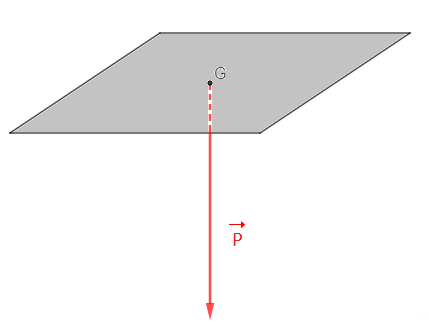
1) Le poids d'une plaque métallique pesant $4.75\;N$
on prend pour échelle $1\;cm \longrightarrow 1\;N$
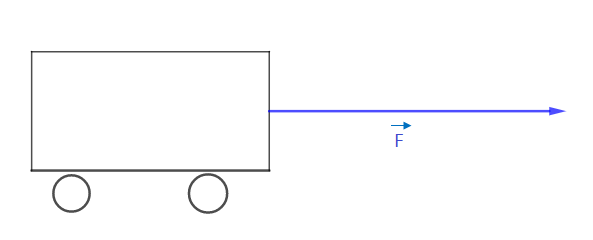
2) La force de traction de $525\;N$ avec laquelle une remorque est déplacée horizontalement.
on prend pour échelle $1\;cm \longrightarrow 105\;N$
Exercice 3
La caisse $C$ de poids $20\;N$ est en équilibre sur une table tel que indiqué par le schéma ci-dessous. $A\ $ et $\ B$ sont deux charges pesant chacune $0.5\;kg$
1) Représentatons toutes les forces agissant sur la caisse $C$
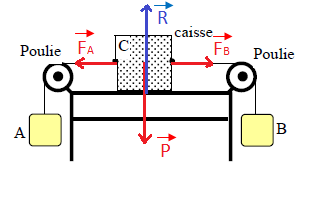
$\vec{R}$ : réaction de la table
$\vec{P}$ : poids de la caisse
$\vec{F}_{B}$ : force exercée par la charge $B$ sur la caisse
$\vec{F}_{A}$ : force exercée par la charge $A$ sur la caisse
2) Représentons le poids de chacune des deux cgarges
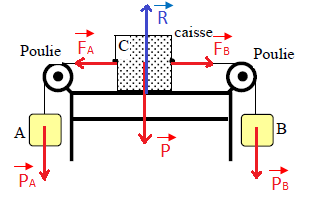
3) Calculons $\|\vec{P}_{A}\|$ et $\|\vec{P}_{B}\|$
On a : $\vec{P}_{A}=m_{A}\times\vec{g}\ $ et $\ \vec{P}_{B}=m_{B}\times\vec{g}\ $ or, $m_{A}=m_{B}$
Donc, $\|\vec{P}_{A}\|=\|\vec{P}_{B}\|=m_{A}\times g$
A.N : $\|\vec{P}_{A}\|=\|\vec{P}_{B}\|=0.5\times 10=5$
D'où, $\boxed{\|\vec{P}_{A}\|=\|\vec{P}_{B}\|=5\;N}$
Exercice 4
1) Le poids $\vec{P}$ d'un objet est la force d'attraction exercée par la terre sur cet objet. C'est une force à distance.
2) Caractéristiques :
$-\ $ point d'application : centre d'inertie de l'objet
$-\ $ droite d'action : verticale
$-\ $ sens : du haut vers le bas
$-\ $ norme (intensité) : $P=m\times g$
Exercice 5
Un objet de masse $500\;g$ est suspendu à un ressort et pend.
1) Représentons, sur un schéma, les forces qui lui sont appliquées
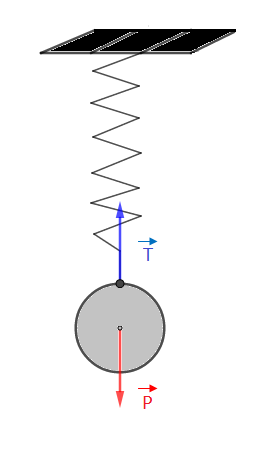
$\vec{T}$ est la tension du ressort.
$\vec{P}$ est le poids de la masse.
2) Donnons les caractéristiques de chacune de ces forces.
$\centerdot\ $ Le poids $\vec{P}$
$-\ $ point d'application : centre d'inertie de la masse
$-\ $ droite d'action : verticale
$-\ $ sens : du haut vers le bas
$-\ $ norme (intensité) : $P=m\times g$
A.N : $P=500\;10^{-3}\times 10=5$
Donc, $\boxed{P=5\;N}$
$\centerdot\ $ La tension $\vec{T}$
$-\ $ point d'application : point de contact entre la masse et le ressort.
$-\ $ droite d'action : verticale
$-\ $ sens : du bas vers le haut
$-\ $ norme (intensité) : $T$
On a : $\vec{T}=-\vec{P}\ \Rightarrow\ T=P$
Donc, $\boxed{T=5\;N}$
Exercice 6
Faisons l'inventaire de toutes les forces qui s'appliquent sur une voiture roulant à vitesse constante sur une route horizontale.
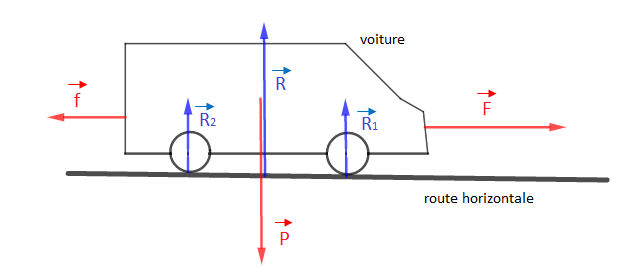
$\vec{R}$ (résultante de $\vec{R}_{1}$ et $\vec{R}_{2}$) : réaction de la route sur la voiture
$\vec{P}$ : poids de la voiture
$\vec{F}$ : force motrice de la voiture (force de déplacement)
$\vec{f}$ : force de frottement sur la voiture (force opposée au déplacement)
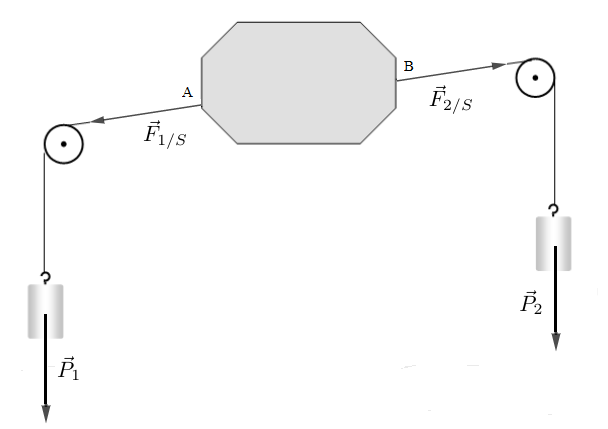
Activité : Condition d'équilibre d'un solide
Une plaque de polystyrène de poids négligeable est soumise à l'action de deux forces par l'intermédiaire de deux fils tendus.
Les deux cylindres accrochés aux deux poulies ont pour masse $50\;g.$
On donne $g=10\;N.kg^{-1}$
1) Calculons l'intensité du poids de chaque cylindre.
Soit $\vec{P}_{1}$ le poids du cylindre relié en $A$ et $\vec{P}_{2}$ le poids du cylindre relié en $B.$
On a : $P_{1}=m_{1}\times g\ $ et $\ P_{2}=m_{2}\times g$
Puisque les deux cylindres sont égales en masse $(m_{1}=m_{2}=m)$ et que l'intensité de la pesanteur $(g)$ est une constante alors, les poids des deux cylindres sont de même intensité.
Par suite, $P_{1}=P_{2}=m\times g$
A.N : $P_{1}=P_{2}=0.05\times 10$
D'où, $\boxed{P_{1}=P_{2}= 0.5\,N}$
2) Représentons le poids des deux cylindres ainsi que les forces $\vec{F}_{1/S}\ $ et $\ \vec{F}_{2/S}$ exercées respectivement en $A\ $ et $\ B.$
$\vec{P}_{1}\ $ et $\ \vec{P}_{2}$ auront pour dimension $2\,cm$, en tenant compte de l'échelle : $1\,cm$ pour $0.25\,N$

Aussi, $F_{1/S}\ $ et $\ F_{2/S}$ sont respectivement égales aux poids $P_{1}\ $ et $\ P_{2}$ des deux cylindre.
Donc, $F_{1/S}=F_{2/S}= 0.5\,N$
Par suite, leur dimension est de $2\,cm$, en utilisant la même échelle.
3) Comme $\left\lbrace\begin{array}{ccc}F_{1/S}&=&P_{1}\\F_{2/S}&=&P_{2}\end{array}\right.$
Et que $P_{1}=P_{2}$ alors, $F_{1/S}=F_{2/S}$
Par ailleurs, $\vec{F}_{1/S}\ $ et $\ \vec{F}_{2/S}$ sont de sens opposés.
Donc, la somme des forces exercées sur la plaque s'annule.
On dit alors que la plaque est en équilibre.
4) Complétons le tableau suivant :
$$\begin{array}{|c|c|c|c|c|}\hline\text{Force}&\text{Point d'application}&\text{Direction}&\text{Sens}&\text{Intensité }(N)\\ \hline&&\text{direction du}&\text{de }A\text{ vers}&\\ \vec{F}_{1/S}&\text{le point }A&\text{fil accroché}&\text{l'extérieur}&0.5\\&&\text{en }A&\text{(centrifuge)}&\\ \hline&&\text{direction du}&\text{de }B\text{ vers}&\\ \vec{F}_{2/S}&\text{le point }B&\text{fil accroché}&\text{l'extérieur}&0.5\\&&\text{en }B&\text{(centrifuge)}&\\ \hline\end{array}$$
5) Nous constatons, d'après le tableau précédent, que les forces $\vec{F}_{1/S}\ $ et $\ \vec{F}_{2/S}$ ont même intensité, même direction, mais sont de sens opposés. Nous en déduisons alors :
$$\vec{F}_{1/S}=-\vec{F}_{2/S}\quad\text{ou encore}\quad\vec{F}_{1/S}+\vec{F}_{2/S}=\vec{0}$$
Exercice 7 : Effets d'une action mécanique
1) Lorsqu'on exerce une action mécanique sur un objet, plusieurs effets sont possibles dont :
$-\ $ un changement de trajectoire
$-\ $ une déformation (étirement, déformation...)
$-\ $ une cassure
2) Pour chaque effet, un exemple est donné dans le tableau ci-dessous :
$$\begin{array}{|l|l|}\hline\text{Effet}&\text{Exemple}\\ \hline\text{changement de}&\text{changement de la trajectoire}\\ \text{trajectoire}&\text{d'un ballon de foot}\\ \hline\text{déformation}&\text{étirement d'un ressort par une masse}\\&\text{accrochée à son extrémité}\\ \hline\text{cassure}&\text{fissure sur un pan de mur}\\ \hline\end{array}$$
Exercice 8 : Types d'actions mécaniques
1) Citons deux exemples d'une action de contact et deux exemples d'une action à distance :
$\centerdot\ $ action de contact :
$-\ $ force de traction d'une voiture
$-\ $ force exercée par la surface de l'eau sur un bateau (poussée d'Archimède)
$\centerdot\ $ action à distance :
$-\ $ force exercée par le soleil sur les planètes du système solaire (force gravitationnelle)
$-\ $ action d'un aimant sur un métal (force magnétique)
2) Citons un exemple d'une action localisée et un exemple d'une action répartie :
$\centerdot\ $ action localisée : action de contact de la pointe d'un clou sur une planche en bois
$\centerdot\ $ action répartie : action du vent sur la voile d'un bateau
Exercice 9 : Reconnaissance de types d'actions mécaniques
Classons dans le tableau suivant, les types d'action en action de contact et en action à distance :
$$\begin{array}{|l|l|} \hline \text{Action de contact}&\text{Action à distance}\\ \hline\text{Action exercée par un pied}&\text{Action exercée par la Terre sur une}\\ \text{sur un ballon.}&\text{mangue qui tombe d'un manguier.}\\&\\ \text{Action exercée par un marteau}&\text{Action exercée par un aimant sur une}\\ \text{sur un clou.}&\text{bille d'acier passant à sa proximité.}\\&\\ \text{Action exercée par le vent}&\\ \text{sur une voile de bateau.}&\\&\\ \text{Action exercée par un homme}&\\ \text{tirant sur la laisse d'un chien.}&\\ \hline\end{array}$$
Exercice 10 : Caractéristiques d'une force
1) Citons les quatre caractéristiques d'une force représentant une action localisée
$-\ $ Point d'application : le point où agit la force ;
$-\ $ Direction : direction de l'action provoquant la force ;
$-\ $ Sens : centripète à l'objet qui subit l'action ;
$-\ $ Norme : l'intensité de la force de l'action subit par l'objet.
2) On représente une force par un vecteur
3) La valeur d'une force est mesurée par un appareil appelé dynamomètre.

Commentaires
Anonyme (non vérifié)
jeu, 03/04/2021 - 20:11
Permalien
svt,maths,pc
Nany Traoré (non vérifié)
mar, 06/29/2021 - 14:52
Permalien
Apprendre
Anonyme (non vérifié)
jeu, 03/18/2021 - 21:39
Permalien
PC forces
Anonyme (non vérifié)
jeu, 03/23/2023 - 15:08
Permalien
Je n'ai rien compris
Alioune ndiaye (non vérifié)
ven, 03/26/2021 - 17:22
Permalien
Figure
Anonyme (non vérifié)
mar, 04/13/2021 - 14:49
Permalien
Interésant
Anonyme (non vérifié)
jeu, 04/22/2021 - 20:47
Permalien
Bon travail excellent
Anonyme (non vérifié)
jeu, 04/22/2021 - 20:47
Permalien
Bon travail excellent
Anonyme (non vérifié)
jeu, 04/22/2021 - 20:58
Permalien
Je voudrais voire la
Sangare Seydou (non vérifié)
ven, 05/28/2021 - 23:56
Permalien
Exercice
Jessica suarez (non vérifié)
mer, 06/29/2022 - 19:21
Permalien
Exo
Jessica suarez (non vérifié)
mer, 06/29/2022 - 19:21
Permalien
Exo
Anonyme (non vérifié)
mer, 06/02/2021 - 00:00
Permalien
Merci
Perle (non vérifié)
sam, 06/19/2021 - 21:38
Permalien
Manque de compréhension
fdini
sam, 06/19/2021 - 23:20
Permalien
$G$ est le centre de
$G$ est le centre de gravité, c'est le point d'application du poids $\vec{P}$
PENDA (non vérifié)
mar, 02/15/2022 - 20:22
Permalien
LE POURQUOI ON A ECRIT G
Anonyme (non vérifié)
mer, 06/29/2022 - 19:23
Permalien
C est parceque c est le
Anonyme (non vérifié)
mer, 06/29/2022 - 19:23
Permalien
C est parceque c est le
Anonyme (non vérifié)
sam, 08/07/2021 - 00:34
Permalien
Bien
Anonyme (non vérifié)
sam, 08/07/2021 - 00:39
Permalien
Bien
Fambaye Diop (non vérifié)
dim, 05/08/2022 - 20:34
Permalien
C est très bien
Fambaye Diop (non vérifié)
dim, 05/08/2022 - 20:34
Permalien
C est très bien
DAME TALLA (non vérifié)
ven, 02/10/2023 - 21:26
Permalien
Savoir
Diallo (non vérifié)
mar, 02/21/2023 - 00:13
Permalien
Aide
Fima (non vérifié)
dim, 02/26/2023 - 15:10
Permalien
Demande
Fa Gadiaga (non vérifié)
ven, 03/03/2023 - 18:32
Permalien
Pour l'exercice de PC , je ne trouve pas sa correction .
Fa Gaadiaga (non vérifié)
ven, 03/03/2023 - 18:37
Permalien
Maintenir le cap
neyla (non vérifié)
mer, 11/15/2023 - 16:16
Permalien
correction
Bsila (non vérifié)
mer, 11/15/2023 - 16:39
Permalien
Une force a une intensité de
Bsila (non vérifié)
mer, 11/15/2023 - 16:39
Permalien
exercice 11 correction
Anonyme (non vérifié)
ven, 02/16/2024 - 19:44
Permalien
Correction exercice 11
diarristadiop17... (non vérifié)
dim, 05/19/2024 - 23:42
Permalien
C'est une bonne application pour apprendre
anonyme (non vérifié)
jeu, 01/09/2025 - 21:34
Permalien
L exercice N 10 a un probleme
Anonyme (non vérifié)
ven, 02/14/2025 - 08:10
Permalien
exercices 11
Anonyme (non vérifié)
dim, 03/23/2025 - 23:12
Permalien
Correction de l'exo 11 svp.
Saïdou Abdoulaye ly (non vérifié)
mer, 04/09/2025 - 21:29
Permalien
Cv incroyable travail
Pages
Ajouter un commentaire