Le quadrilatère - 5e

Classe: 
Cinquième
 

I. Définition

On appelle quadrilatère toute figure géométrique ayant quatre côtés.
 
Comme exemple nous citerons le trapèze, le parallélogramme mais aussi le rectangle, le carré, le losange qui sont des parallélogrammes particuliers.

II. Le parallélogramme

II.1. Activité

1) Tracez un segment $[AB]$ de $6\;cm$ de longueur.
 
2) Placez un point $O$ n'appartenant pas à $[AB]$ tel que :
$$OA=2\;cm\quad\text{et}\quad OB=5\;cm$$
3) Construire les points $C\ $ et $\ D$ tels que :
$$D=S_{O}(B)\quad\text{et}\quad C=S_{O}(A)$$
4) Comment sont les droites $(AB)\ $ et $\ (DC)\ ?\ (AD)\ $ et $\ (BC)\ ?$
 
5) Comparer les longueurs entre $AB\ $ et $\ DC\ $ et entre $\ AD\ $ et $\ BC$

Solution

1) 2) 3) (voir figure)

 

 
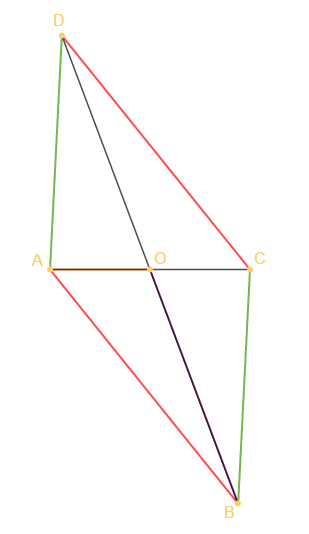
4) Les droites $(AB)\ $ et $\ (DC)$ sont parallèles.
 
De même, les droites $(AD)\ $ et $\ (BC)$ sont parallèles.
 
5) Les longueurs entre $AB\ $ et $\ DC$ et entre $AD\ $ et $\ BC$ sont les mêmes.

II.2. Définition

On appelle parallélogramme tout quadrilatère dont les côtés sont deux à deux parallèles et de même longueur.

II.3. Propriétés

Dans un parallélogramme :
 
$-\ $ les diagonales se coupent en leur milieu
 
$-\ $ les deux angles opposés ont la même mesure
 
$-\ $ deux angles consécutifs sont supplémentaires

Application

1) Construire un parallélogramme $ABCD$ tel que
$$AB=6\;cm\quad\text{et}\quad BC=3\;cm$$
2) Construire un parallélogramme $ABCD$ tel que
$$mes\,\hat{A}=45^{\circ}\quad\text{et}\quad mes\,\hat{B}=135^{\circ}$$

Solution

1)

 

 
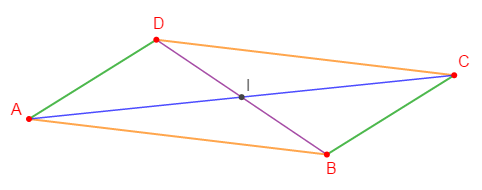
2)

 

 

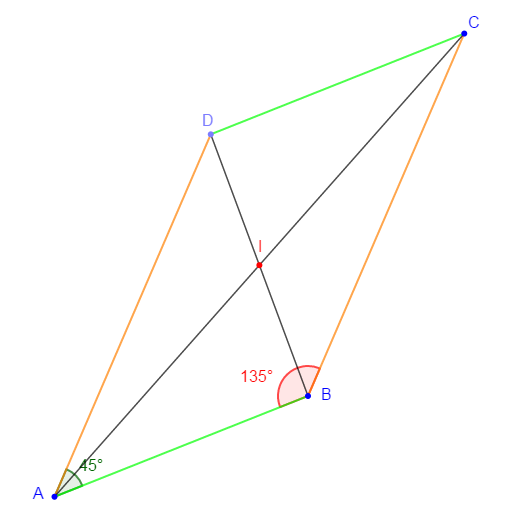
III. Le losange

III.1. Activités

1) Tracez un segment $[AC]$ perpendiculaire au segment $[BD]$ en leur milieu $O$ tel que
$$AC=6\;cm\quad\text{et}\quad BD=3\;cm$$
2) Que représente le quadrilatère $ABCD\ ?$
 
3) Est-ce que toutes les propriétés du parallélogramme sont respectées ? sinon précise les autres propriétés par la figure.

Solution

1)

 

 
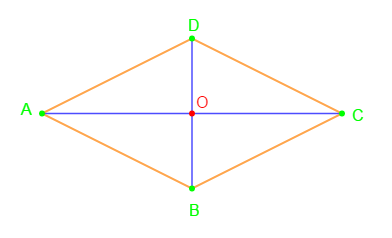
2) Le quadrilatère $ABCD$ est un parallélogramme.
 
3) On vérifie que toutes les propriétés du parallélogramme sont respectées.
 
De plus, d'après la figure, on constate que deux côtés consécutifs ont même longueur.

III.2. Définition

Un losange est un parallélogramme dont deux côtés consécutifs ont même longueur.

III.3. Propriétés

Dans un losange :
 
$-\ $ deux côtés consécutifs ont même longueur
 
$-\ $ les diagonales sont perpendiculaires
 
$-\ $ une diagonale est en même temps bissectrice

Application

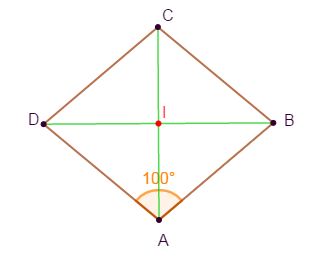
Construire un losange $ABCD$ tel que :
$$AB=3\;cm\quad\text{et}\quad mes\,\hat{A}=100^{\circ}$$

Solution

 


 
 
Auteur: 
Mamadou Siradji Dia

Commentaires

Anonyme (non vérifié)

mer, 04/28/2021 - 03:07

Comment démontre que des point sont alignés

Anonyme (non vérifié)

mer, 04/28/2021 - 03:07

Comment démontre que des point sont alignés

Anonyme (non vérifié)

mer, 04/28/2021 - 03:08

Comment on démontre que les point sont alignés

Ajouter un commentaire