Solution des exercices : Dosage acide - base - Ts
Classe:
Terminale
Exercice 1
1) Bilan de matière des ions hydronium et hydroxyde :
$$\begin{array}{|c|ccccccc|} \hline \text{Etat du système}&H_{3}O^{+}&\ &+\ OH^{-}&\ &\rightarrow&\ &2H_{2}O\\ \hline \text{Avancement}& &|&nH_{3}O^{+}&|&n_{OH^{-}}&|&n_{H_{2}O}\\ \hline \text{Etat initial}& &|&n_{A}&|&n_{B}&|&\text{Excès}\\ \hline \text{Etat intermédiaire}&x&|&n_{A}-x&|&n_{B}-x&|&\text{Excès}\\ \hline \text{Etat final}&x_{max}&|&n_{A}-x_{max}&|&n_{B}-x_{max}&|&\text{Excès}\\ \hline \end{array}$$
$\begin{array}{lcl} n_{B}-x_{max}&=&0\\&\Rightarrow&x_{max}=n_{B} \end{array}$
$\begin{array}{lcl} n_{A}-x_{max}&=&0\\&\Rightarrow&x_{max}=n_{A}\\&\Rightarrow& n_{B}=n_{A} \end{array}$
2) Calcul de la concentration molaire de la solution après neutralisation :
$\bullet\ \ $ $V_{A}=200\,mL\;,\ pH_{A}=2.0\text{ et }V_{B}=200\,mL\;,\ pH_{B}=12.0.$
$\begin{array}{lcl} n_{A}&=&C_{A}V_{A}\\&=&10^{-pH_{A}}V_{A}\\&=&10^{-2}\times200\cdot10^{-3}\\&=&2.0\cdot10^{-3}mol \end{array}$
$\begin{array}{lcl} n_{B}&=&C_{B}V_{B}\\&=&10^{-pH_{B}}V_{B}\text{ avec }C_{B}\\&=&\left[OH^{-}\right]\\&=&\dfrac{K_{e}}{10^{-pH_{B}}}\\&=&10^{14+pH_{B}}\\&\Rightarrow&n_{B}=10^{-14+pH_{B}}V_{B}\\&=&10^{-14+12.0}\times200\cdot10^{-3}\\&=&2.0\cdot10^{-3}mol\\&\Rightarrow&\dfrac{n_{A}}{1}=\dfrac{n_{B}}{1} \end{array}$
La réaction est totale.
La solution est neutre et $pH=7$
$\bullet\ \ $ $V_{A}=800\,mL\;,\ pH_{A}=2.0\text{ et }V_{B}=500\,mL\;,\ pH_{B}=12.0.$
$\begin{array}{lcl} n_{A}&=&C_{A}V_{A}\\&=&10^{-pH_{A}}V_{A}\\&=&10^{-2}\times800\cdot10^{-3}\\&=&8.0\cdot10^{-3}mol \end{array}$
$\begin{array}{lcl} n_{B}&=&10^{-14+pH_{B}}V_{B}\\&=&10^{-14+12.0}\times500\cdot10^{-3}\\&=&5.0\cdot10^{-3}mol \end{array}$
$\dfrac{n_{A}}{1}>\dfrac{n_{B}}{1}$, l'acide $HCl$ est en excès, la base $NaOH$ est le réactif limitant
$\begin{array}{lcl} \left[H_{3}O^{+}\right]&=&\dfrac{C_{A}V_{A}-C_{B}V_{B}}{V_{A}+V_{B}}\\&\Rightarrow&pH=-\log\dfrac{C_{A}V_{A}-C_{B}V_{B}}{V_{A}V_{B}}\\&=&-\log\dfrac{8.0\cdot10^{-3}-5.0\cdot10^{-3}}{800\cdot10^{-3}+500\cdot10^{-3}}\\&\Rightarrow&pH=2.6 \end{array}$
$\bullet\ \ $ $V_{A}=300\,mL\;,\ pH_{A}=2.0\text{ et }V_{B}=200\,mL\;,\ pH_{B}=12.3.$
$\begin{array}{lcl} n_{A}&=&C_{A}V_{A}\\&=&10^{-pH_{A}}V_{A}\\&=&10^{-2}\times300\cdot10^{-3}\\&=&3.0\cdot10^{-3}mol \end{array}$
$\begin{array}{lcl} n_{B}&=&C_{B}V_{B}\\&=&10^{-14+pH_{B}}V_{B}\\&=&10^{-14+12.3}\times200\cdot10^{-3}\\&=&6.0\cdot10^{-3}mol \end{array}$
$\dfrac{n_{B}}{1}>\dfrac{n_{A}}{1}$, la base $NaOH$ est en excès, l'acide est le réactif limitant
$\begin{array}{lcl} \left[OH^{-}\right]&=&\dfrac{C_{B}V_{B}-C_{A}V_{A}}{V_{A}+V_{B}}\\&\Rightarrow&pH=14+\log\dfrac{C_{B}V_{B}-C_{A}V_{A}}{V_{A}V_{B}}\\&=&14+\log\dfrac{6.0\cdot10^{-3}-3.0\cdot10^{-3}}{300\cdot10^{-3}+200\cdot10^{-3}}\\&\Rightarrow&pH=11.3 \end{array}$
3) Calcule de la concentration molaire des ions sodium et des ions chorure en solution dans trois cas.
$\bullet\ \ $ $V_{A}=200\,mL\;,\ pH_{A}=2.0\text{ et }V_{B}=200\,mL\;,\ pH_{B}=12.0.$
$\begin{array}{lcl} \left[Cl^{-}\right]&=&\dfrac{C_{A}V_{A}}{V_{A}+V_{B}}\\&=&\dfrac{10^{-pH_{A}}V_{A}}{V_{A}+V_{B}}\\&=&\dfrac{10^{-2}\times200\cdot10^{-3}}{200\cdot10^{-3}+200\cdot10^{-3}}\\&\Rightarrow&\left[Cl^{-}\right]=5.0\cdot10^{-3}mol\cdot L^{-1} \end{array}$
$\begin{array}{lcl} \left[Na^{+}\right]&=&\dfrac{C_{B}V_{B}}{V_{A}+V_{B}}\\&=&\dfrac{10^{-14+pH_{B}}V_{B}}{V_{A}+V_{B}}\\&=&\dfrac{10^{-14+12}\times200\cdot10^{-3}}{200\cdot10^{-3}+200\cdot10^{-3}}\\&\Rightarrow&\left[Na^{+}\right]=5.0\cdot10^{-3}mol\cdot L^{-1} \end{array}$
$\bullet\ \ $ $V_{A}=800\,mL\;,\ pH_{A}=2.0\text{ et }V_{B}=500\,mL\;,\ pH_{B}=12.0.$
$\begin{array}{lcl} \left[Cl^{-}\right]&=&\dfrac{C_{A}V_{A}}{V_{A}+V_{B}}\\&=&\dfrac{10^{-pH_{A}}V_{A}}{V_{A}+V_{B}}\\&=&\dfrac{10^{-2}\times800\cdot10^{-3}}{800\cdot10^{-3}+500\cdot10^{-3}}\\&\Rightarrow&\left[Cl^{-}\right]=6.2\cdot10^{-3}mol\cdot L^{-1} \end{array}$
$\begin{array}{lcl} \left[Na^{+}\right]&=&\dfrac{C_{B}V_{B}}{V_{A}+V_{B}}\\&=&\dfrac{10^{-14+pH_{B}}V_{B}}{V_{A}+V_{B}}\\&=&\dfrac{10^{-14+12}\times500\cdot10^{-3}}{800\cdot10^{-3}+500\cdot10^{-3}}\\&\Rightarrow&\left[Na^{+}\right]=3.8\cdot10^{-3}mol\cdot L^{-1} \end{array}$
$\bullet\ \ $ $V_{A}=300\,mL\;,\ pH_{A}=2.0\text{ et }V_{B}=200\,mL\;,\ pH_{B}=12.3.$
$\begin{array}{lcl} \left[Cl^{-}\right]&=&\dfrac{C_{A}V_{A}}{V_{A}+V_{B}}\\&=&\dfrac{10^{-pH_{A}}V_{A}}{V_{A}+V_{B}}\\&=&\dfrac{10^{-2.0}\times300\cdot10^{-3}}{300\cdot10^{-3}+200\cdot10^{-3}}\\&\Rightarrow&\left[Cl^{-}\right]=6.0\cdot10^{-3}mol\cdot L^{-1} \end{array}$
$\begin{array}{lcl} \left[Na^{+}\right]&=&\dfrac{C_{B}V_{B}}{V_{A}+V_{B}}\\&=&\dfrac{10^{-14+pH_{B}}V_{B}}{V_{A}+V_{B}}\\&=&\dfrac{10^{-14+12.3}\times200\cdot10^{-3}}{300\cdot10^{-3}+200\cdot10^{-3}}\\&\Rightarrow&\left[Na^{+}\right]=8.0\cdot10^{-3}mol\cdot L^{-1} \end{array}$
Exercice 2
1) Montrons que la concentration $C$ est voisine de $6\,mol\cdot L^{-1}$
$\begin{array}{lcl} C&=&\dfrac{m}{MV}\\&=&\dfrac{20\%m_{S}}{MV}\\&=&\dfrac{20\%\rho\,V}{MV}\\&=&\dfrac{20\%\rho}{M}\\&\Rightarrow&C=\dfrac{0.20\times 1000\times 1.2}{40}\\&\Rightarrow& C=6\,mol\cdot L^{-1} \end{array}$
2) Volume de la solution commerciale à prélever.
Au cours de la dilution le nombre de la base, le nombre de moles de la base reste constant :
$\begin{array}{lcl} n_{B}&=&CV_{0}\\&=&CV\\&\Rightarrow& V_{0}=\dfrac{CV}{C}\\&=&\dfrac{3\cdot 10^{-2}}{C}\\&\Rightarrow& V_{0}5\,mL \end{array}$
3) a) Une base est une espèce chimique susceptible de capter au moins un proton
b) Calcule du $pH$ de la solution diluée
$pH=14+\log\,C=14+\log\,3\cdot 10^{-2}\Rightarrow pH=12.5$
4) a) Équation de la réaction :
$H_{3}O^{+}\ +\ OH^{-}\ \rightarrow\ 2H_{2}O$ ou
$HCl\ +\ NaOH\ \rightarrow\ NaCl\ +\ H_{2}O$
b) Calcule de la concentration de la solution diluée :
$\Rightarrow C_{B}=\dfrac{C_{A}V_{A}}{V_{B}}=\dfrac{1\cdot 10^{-2}\times 15}{5}$
$n_{B}=n_{A}\Rightarrow C_{B}V_{B}=C_{A}V_{A}\Rightarrow C_{B}=3\cdot 10^{-2}mol\cdot L^{-1}$
On retrouve bien la valeur souhaitée
Exercice 3
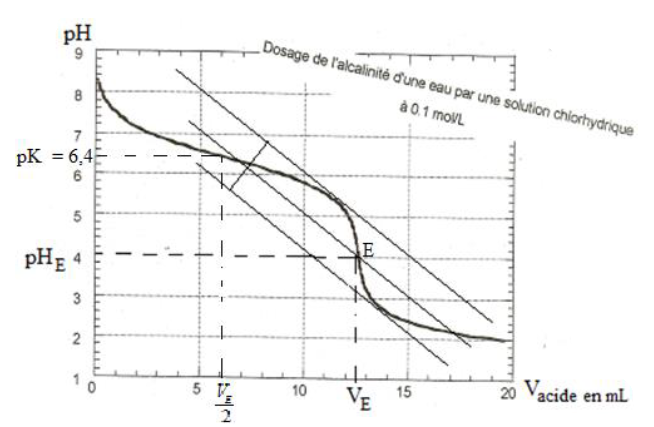
1) a) Les coordonnées du point d'équivalence : $E\left(pH_{E}=4\ ;\ V_{E}=12.5\,mL\right)$
b) Le $pK_{A}$ de la base est : $pK_{A}=6.4$
2) Équation de la réaction de dosage :
$HCO_{3}^{-}\ +\ H_{3}O^{+}\ \rightarrow\ H_{2}CO_{3}$
Concentration molaire de la base :
$\begin{array}{lcl} C_{B}&=&\dfrac{C_{A}V_{A}}{V_{B}}\\&=&\dfrac{1\cdot 10^{-1}\times 12.5}{50}\\&\Rightarrow& C_{B}=2.5\cdot 10^{-2}mol\cdot L^{-1} \end{array}$
Concentration massique de la base :
$\begin{array}{lcl} C_{m_{B}}&=&C_{B}\times M_{HCO_{3}^{-}}\\&=&2.5\cdot 10^{-2}\times(1.0+12+3\times16)\\&\Rightarrow&C_{m_{B}}=1.5\,g\cdot L^{-1} \end{array}$
3) Détermination du titre alcalimétrique $T.A.C$
$\begin{array}{lcl} C_{B}V_{B}&=&C_{A}V_{A}\\&\Rightarrow&V_{A}=\dfrac{C_{B}V_{B}}{C_{A}}\\&=&\dfrac{2.5\cdot 10^{-2}\times 100}{2\cdot 10^{-2}}\\&\Rightarrow& V_{A}=125\,mL \end{array}$
Exercice 4
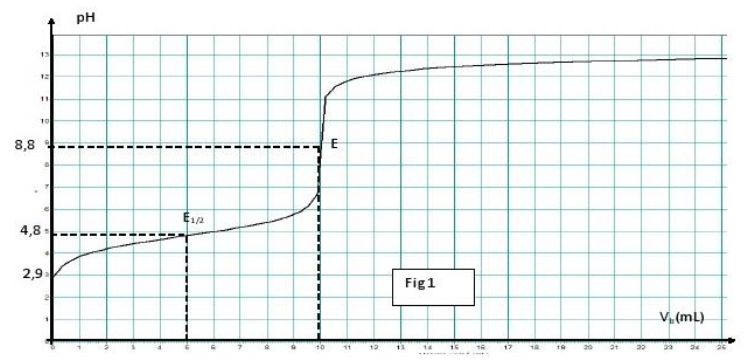
1) a) La courbe est croissante : on part d'un $pH$ acide et on atteint des $pH$ basiques
Cette courbe comporte quatre parties essentielles :
$\bullet\ \ 0\,mL\leq V_{b}\geq 5\,mL$ où le $pH$ croit assez nettement
$\bullet\ \ 5\,mL\leq V_{b}\geq 9\,mL$ où le $pH$ varie peu, la courbe est quasiment rectiligne ;
$\bullet\ \ 9\,mL\leq V_{b}\geq 13\,mL$, où l'on observe une variation de $pH$, brusque mais moins importante que pour l'acide fort
$\bullet\ \ V_{b}\geq 3\,mL$ où le $pH$ varie faiblement et tend vers une asymptote horizontale
b) L'acide $AH$ est un acide faible puisque la courbe présente deux points d'inflexion $E$ et $E_{1/2}$
2) a) La valeur du $PH$ à l'équivalence est déterminée par méthode des tangentes : $pH=8.8$
b) La constante d'acidité $pK_{A}$ du couple $AH/A^{-}$ correspond à l'ordonnée du volume à la demi-équivalence $pK_{A}=4.8$
3) Le point d'équivalence d'un tirage ou plus largement d'une réaction chimique est le point où l'espèce chimique à tirer et l'espèce titrante ont été mélangés dans des proportions stoechiométriques.
A l'équivalence du tirage, ces deux espèces sont complètement consommées et donc leur quantité de matière est nulle.
$\bullet\ \ $Calcul de la concentration $C_{A}$ de la solution de l'acide $AH$
A l'équivalence :
$\begin{array}{lcl} C_{A}V_{A}&=&C_{B}V_{B}\\&\Rightarrow& C_{A}=\dfrac{C_{B}V_{B}}{V_{A}}\\&=&\dfrac{0.1\times 10}{20}\\&\Rightarrow& C_{A}=0.1\,mol\cdot L^{-1} \end{array}$
4) a) Équation de la réaction de dosage
$$AH\ +\ OH\ \rightarrow\ A^{-}\ +\ H_{2}O$$
Montrons que la réaction est pratiquement totale
$\begin{array}{lcl} K_{R}&=&\dfrac{[A^{-}]}{[AH][OH^{-}]}\\&=&\dfrac{[A^{-}]\left[H_{3}O^{+}\right]}{[AH]\left[OH^{-}\right]\left[H_{3}O^{+}\right]}\\&=&\dfrac{K_{A}}{Ke}\\&\Rightarrow&K_{R}=\dfrac{10^{-4.8}}{10^{-14}}\\&=&10^{9.2}\\&\Rightarrow&K_{R}>10^{4} \end{array}$
La réaction est pratiquement totale
b) A l'équivalence la solution est une solution de base faible : la solution est donc basique
c) Vérifions que le $pH$ à l'équivalence $E$ est donné par la relation :
$pH_{E}=\left(pKe+pKa+\log\,C'_{AE}\right)$
Pour $pKa=4.8\quad C'_{AE}=\dfrac{C_{B}V_{B}}{V_{A}+V_{B}}\Rightarrow$
$\begin{array}{lcl} pH&=&\dfrac{1}{2}\left(14+pK_{A}+\log\dfrac{C_{B}V_{B}}{V_{A}+V_{B}}\right)\\&=&\dfrac{1}{2}\left(14+4.8+\log\dfrac{0.1\times 10}{20+10}\right)\\&\Rightarrow& pH=8.7\\&\Rightarrow&pH_{E}=8.8 \end{array}$
5) a)
$\bullet\ \ $Le $Ph$ diminue avec la concentration qui diminue avec la dilution.
Le $pH$ initial de la solution acide augmente donc avec la dilution
$\bullet\ \ $La dilution n'a pas d'effet sur le $pH$ à la demi-équivalence, car ce $pH$ est indépendant de la concentration ; car il faut $pH=pK_{A}$
$\bullet\ \ $La dilution n'a pas d'effet sur le volume $V_{BE}$ de base versé à l'équivalence car, cette dilution apporte autant ions $H_{3}O^{+}$ que d'ions $OH^{-}$
$\bullet\ \ $Le $pH$ à l'équivalence augmente avec la dilution car la concentration diminue
b) Calcule du volume $Ve$ d'eau
Au cours de la dilution, le nombre moles d'acide reste contant :
$\begin{array}{lcl} n_{A}&=&C'_{AE}\left(V_{e}+V_{a}\right)V_{e}\\&=&C_{A}V_{a}\\\Rightarrow V_{e}&=&\left(\dfrac{C_{A}}{C'_{AE}}-1\right)V_{a}\\\Rightarrow V_{e}&=&\left(\dfrac{C_{A}}{10^{2\,pH_{E}-\left(pK_{A}+pK_{e}\right)}}-1\right)V_{a}\\\Rightarrow V_{e}&=&\left(\dfrac{10^{-1}}{10^{2\times(8.8-0.15)-(4.8+14)}}-1\right)V_{a}\\\Rightarrow V_{e}&=&43\,mL \end{array}$
6) a) La teinte sensible d'un indicateur coloré correspond à la zone de virage de cet indicateur coloré (ou la teinte sensible est le nom donné à la couleur que prend la solution dans la zone de virage).
b) La phénolphtatéine est l'indicateur approprié car le $pH$ à l'équivalence $\left(pH_{E}=8.8\right)$ appartient à la zone de virage cet indicateur $(8.2-10.0)$
Exercice 5
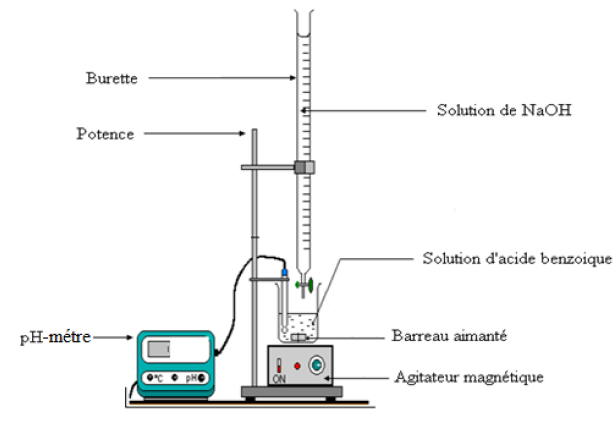
1) Schéma annoté du dispositif
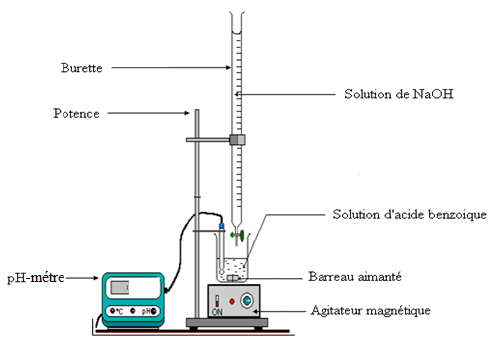
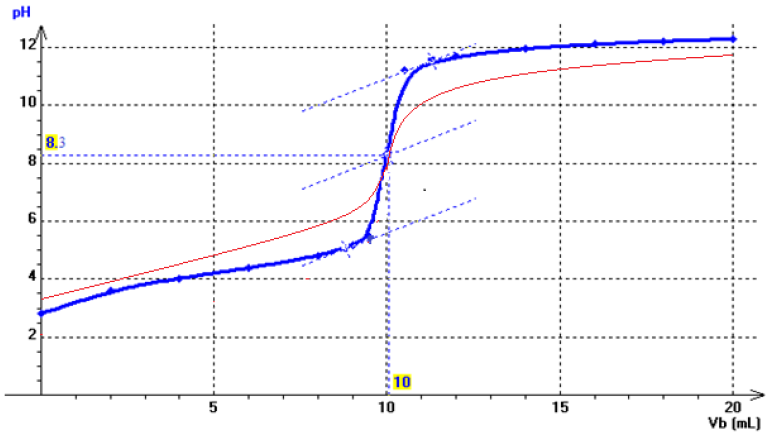
2) Tracé de la courbe
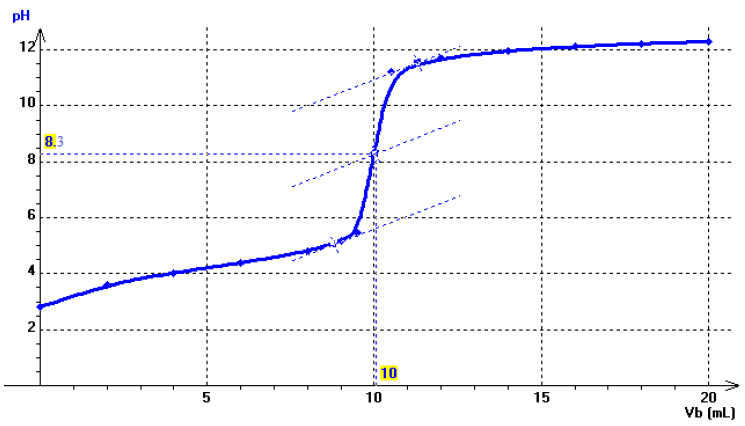
3) a) A l'équivalence à $pH_{E}=8.3$ et il s'agit d'un acide faible (pour un dosoge d'un acide fort par une base forte, à l'équivalence, $pH_{E}=7$)
b) A la demi-équivalence : $pH=pK_{A}=4.2$ et l'acide est l'acide benzoique
c) La valeur du $pH$ initial est : $pH=2.81$
$-\ $ Calcule de la concentration $C_{a}$ de l'aide
L'acide est faiblement dissocié :
$\begin{array}{lcl} pH&=&\dfrac{1}{2}\left(pK_{A}-\log\,C_{a}\right)\\&\Rightarrow& C_{a}=10^{-2pH+pK_{A}}\\&=&10^{-2\times 2.81+4.2}\\&\Rightarrow& C_{a}=3.8\cdot10^{-2}mol\cdot L^{-1} \end{array}$
4) Équation de la réaction du dosage :
$C_{6}H_{5}COOH\ +\ OH^{-}\ \rightarrow\ C_{6}H_{5}CO^{-}\ +\ H_{2}O$
5) Calcule de la concentration $C_{b}$ de la base :
A l'équivalence :
$\begin{array}{lcl} n_{b}&=&n_{a}\\&\Rightarrow& C_{a}V_{b}=C_{a}V_{a}\\&\Rightarrow& C_{b}=\dfrac{C_{a}V_{a}}{V_{b}}\\&=&\dfrac{3.8\cdot10^{-2}\times 20}{10}\\&\Rightarrow&C_{b}=7.6\cdot10^{-2}mol\cdot L^{-1} \end{array}$
6) Tracé de la courbe
Exercice 6
1) a) Cette solution est basique car son $pH$ est supérieur à $7$
b) L'espèce conjuguée est l'ion ammonium de formule : $NH_{4}^{+}$
c) Le couple acide-base auquel appartient l'ammoniac est : $NH_{4}^{+}|NH_{3}$
d) Diagramme de prédominance, en fonction de $pH$, des espèce de ce couple

Le $pH>pK_{A}\;,\ NH_{3}$ est l'espèce prédominante dans la solution $S$
2) a) Équation de la réaction support du dosage
$H_{3}O^{+}\ +\ NH_{3}\ \rightarrow\ NH_{4}^{+}\ +\ H_{2}O$ ou
$HCl\ +\ NH_{3}\ \rightarrow\ NH_{4}^{+}\ +\ Cl^{-}\ +\ H_{2}O$
La transformation chimique est rapide et totale
b) Expression de la constante d'équilibre $K_{r}$ en fonction de la constante d'acidité $Ka.$
$\begin{array}{lcl} K_{r}&=&\dfrac{\left[NH_{4}^{+}\right]}{\left[H_{3}O^{+}\right]\left[NH_{3}\right]}\\&\text{or }K_{A}&=\dfrac{\left[H_{3}O^{+}\right]\left[NH_{3}\right]}{\left[NH_{4}^{+}\right]}\\&\Rightarrow&K_{r}=\dfrac{1}{K_{A}} \end{array}$
Calculer sa valeur de la constante de réaction
$\begin{array}{lcl} K_{r}&=&\dfrac{1}{K_{A}}\\&=&\dfrac{1}{6.3\cdot10^{-10}}\\&\Rightarrow&K_{r}=1.6\cdot10^{9} \end{array}$
$K_{r}\geq 10^{4}$, la réaction est totale
c) Détermination de la concentration molaire $C$ de la solution
A l'équivalence :
$\begin{array}{lcl} n_{B}&=&n_{A}\\&\Rightarrow& CV=C_{A}V_{A}\\&\Rightarrow& C=\dfrac{C_{A}V_{A}}{V}\\&=&\dfrac{5.00\cdot10^{-1}\times10.8}{10.0}\\&\Rightarrow&C=5.40\cdot10^{-1}mol\cdot L^{-1} \end{array}$
Concentration $C_{0}$ de la solution commerciale
$\begin{array}{lcl} C&=&\dfrac{C_{0}}{20}\\&\Rightarrow&C_{0}=20C\\&=&20\times5.40\cdot10^{-1}\\&\Rightarrow&C_{0}=10.8\,mol\cdot L^{-1} \end{array}$
d) Détermination de l'expression du pourcentage massique de la solution commerciale en fonction de $C_{0}$ ; $M$ et $\mu.$
$\begin{array}{lcl} C_{0}&=&\dfrac{m_{NH_{3}}}{M\times V_{\text{Solution}}}\\&=&\dfrac{x\times m_{\text{Solution}}}{M\times V_{\text{Solution}}}\\&=&\dfrac{x\times\mu\times V_{\text{Solution}}}{M\times V_{\text{Solution}}}\\&=&\dfrac{x\times\mu}{M}\\&\Rightarrow& x=\dfrac{C_{0}M}{\mu}\\&=&\dfrac{10.8\times 17}{920}\\&\Rightarrow&x=0.20\ ;\ \text{soit }x=20\% \end{array}$
Cette valeur correspond bien au pourcentage massique de l'ammoniac
3) a) Détermination les quantités de matière $n_{1}$ d'ammoniac et $n_{2}$ d'acide chlorhydrique introduites
$\begin{array}{lcl} n_{1}&=&CV\\&=&5.4\cdot10^{-1}\times10.0\cdot10^{-3}\\&\Rightarrow&n_{1}=5.4\cdot10^{-3}mol \end{array}$
$\begin{array}{lcl} n_{2}&=&C_{A}V_{A}\\&=&5.00\cdot10^{-1}\times6.0\cdot10^{-3}\\&\Rightarrow&n_{2}=3.0\cdot10^{-3}mol \end{array}$
b) Détermination de l'avancement final, l'avancement maximal à l'aide d'un tableau descriptif de l'évolution du système chimique
$$\begin{array}{|c|c|ccccccc|} \hline \text{Système}&\text{Avancement}&H_{3}O^{+}\ &+&\ NH_{3}\ &\rightarrow&NH_{4}^{+}&+&\ H_{2}O\\ \hline \text{Initial}&x=0&0&|&5.4\cdot10^{-3}&|&0&|&0\\ \hline \text{Intermédiaire}&x&C_{A}V_{A}-x&|&5.4\cdot10^{-3}-x&|&x&|&x\\ \hline \text{Final}&x_{f}&C_{A}V_{A}-x_{f}&|&5.4\cdot10^{-3}-x_{f}&|&x_{f}&|&x_{f}\\ \hline \end{array}$$
L'avancement final correspond à :
$5.4\cdot10^{-3}-x_{f}=0\Rightarrow x_{f}=5.4\cdot10^{-3}mol$
Lorsque la quantité initiale de base introduite est consommée l'avancement est maximal : $x_{f}=x_{max}$
c) Montrons que la transformation est quasi-totale
$\tau=\dfrac{x_{f}}{n_{B}}=\dfrac{x_{f}}{CV}=\dfrac{5.4\cdot10^{-3}}{5.4\cdot10^{-1}\times10.0\cdot10^{-3}}$
$$\Rightarrow\tau=1$$
La transformation est quasi-totale
Exercice 7
1) Schéma annoté du dispositif expérimental
2) Tracé des courbes $pH_{1}=f\left(V_{B1}\right)$ et $pH_{2}=f\left(V_{B2}\right)$

3) Identification sur le graphique de l'acide fort et l'acide faible
$AH_{1}$ est l'acide fort et $AH_{2}$ est l'acide faible
4) Calcule des concentration des deux acides
A l'équivalence :
$-\ $ acide fort :
$\begin{array}{lcl} n_{AH_{1}}&=&n_{b}\\&\Rightarrow&C_{AH_{1}}V_{AH_{1}}\\&=&C_{b}V_{E}\\&\Rightarrow&C_{AH_{1}}=\dfrac{C_{b}V_{E}}{V_{AH_{1}}}\\&\Rightarrow&C_{AH_{1}}=\dfrac{0.1\times10}{10}\\&\Rightarrow&C_{AH_{1}}=10^{-1}mol\cdot L^{-1} \end{array}$
$-\ $ acide faible :
$\begin{array}{lcl} n_{AH_{2}}&=&n_{b}\\&\Rightarrow&C_{AH_{2}}V_{AH_{2}}\\&=&C_{b}V_{E}\\&\Rightarrow&C_{AH_{2}}=\dfrac{C_{b}V_{E}}{V_{AH_{2}}}\\&\Rightarrow&C_{AH_{2}}=\dfrac{0.1\times10}{10}\\&\Rightarrow&C_{AH_{2}}=10^{-1}mol\cdot L^{-1} \end{array}$
5) Détermination du $pK_{A}$ et la constante d'acidité $K_{A}$ de l'acide faible.
A la demi-équivalence : $pH=pK_{A}=4.8$
$K_{A}=10^{-pK_{A}}=10^{-4.8}=1.6\cdot10^{-5}$
6) Valeur $pH$ de la solution acide lorsqu'on continue à ajouter la solution
Après l'équivalence, la solution est basique :
$\begin{array}{lcl} pH&=&14+\log\,C'_{b}\\&=&14+\log\dfrac{C_{b}V_{b}-C_{a}V_{a}}{V_{b}+V_{a}}\\&=&14+\log\dfrac{V_{b}\left(C_{b}-C_{a}\dfrac{V_{a}}{V_{b}}\right)}{V_{a}\left(1+\dfrac{V_{a}}{V_{b}}\right)}\\&=&14+\log\dfrac{\left(C_{b}-C_{a}\dfrac{V_{a}}{V_{b}}\right)}{\left(1+\dfrac{V_{a}}{V_{b}}\right)}\\\\&\Rightarrow&pH=14+\log\,C_{b}\\&=&14+\log0.1V_{b}V_{a}\\&\Rightarrow&\dfrac{V_{a}}{V_{b}}\approx 0\\&\Rightarrow&pH=13 \end{array}$
Exercice 8
1) Montrons que la concentration molaire $C$ est voisine de $6\,mol\cdot L^{-1}$
$\begin{array}{lcl} C&=&\dfrac{n}{V}\\&=&\dfrac{m}{MV}\\&=&\dfrac{20\%m_{\text{}Solution}}{MV}\\&=&\dfrac{20\%\rho V}{MV}\\&=&\dfrac{20\%\rho}{M}\\&=&\dfrac{20\%\mathrm{d}\rho_{eau}}{M}\\&\Rightarrow&C=\dfrac{0.20\times1.2\times1000}{40}\\&\Rightarrow&C=6\,mol\cdot L^{-1} \end{array}$
2) Volume de la solution commerciale à prélever
Au cours de la dilution le nombre de moles de la soude reste constant :
$\begin{array}{lcl} n_{b}&=&CV\\&=&C'V'\\&\Rightarrow&V=\dfrac{C'V'}{C}\\&\Rightarrow&V=\dfrac{3\cdot10^{-2}\times1}{6}\\&\Rightarrow&V=5\,mL \end{array}$
3) a) Une base forte est une base qui s'ionise totalement dans l'eau en donnant des ions $HO^{-}$
b) Calcul du pH de la solution diluée
$pH=14+\log\,C'=14+\log3\cdot10^{-2}\Rightarrow pH=12.5$
4) a) Équation – bilan de la réaction
$$H_{3}O^{+}\ +\ OH^{-}\ \rightarrow\ 2H_{2}O\quad\text{ou}$$
$$HCl\ +\ NaOH\ \rightarrow\ NaCl\ +\ H_{2}O$$
b) Calcul de la concentration de la solution diluée
A l'équivalence :
$\begin{array}{lcl} n_{b}&=&n_{a}\\&=&C_{b}V_{b}\\&=&C_{a}V_{a}\\&\Rightarrow&C_{b}=\dfrac{C_{a}V_{a}}{V_{b}}\\&\Rightarrow&V=\dfrac{10^{-2}\times15}{5}\\&\Rightarrow&C_{b}=3\cdot10^{-2}mol\cdot L^{-1} \end{array}$
On retrouve bien la valeur souhaitée.
Exercice 9
1) a) Représentation graphique $pH=f(x)$
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|} \hline \dfrac{V_{B}}{V_{A}}&\dfrac{1}{5}&\dfrac{1}{4}&\dfrac{1}{3}&\dfrac{1}{2}&1&2&3&4&5\\ \hline x&-0.7&-0.6&-0.5&-0.3&0&0.3&0.5&0.6&0.7\\ \hline pH&3.1&3.2&3.3&3.5&3.8&4.1&4.3&4.4&4.5\\ \hline \end{array}$$
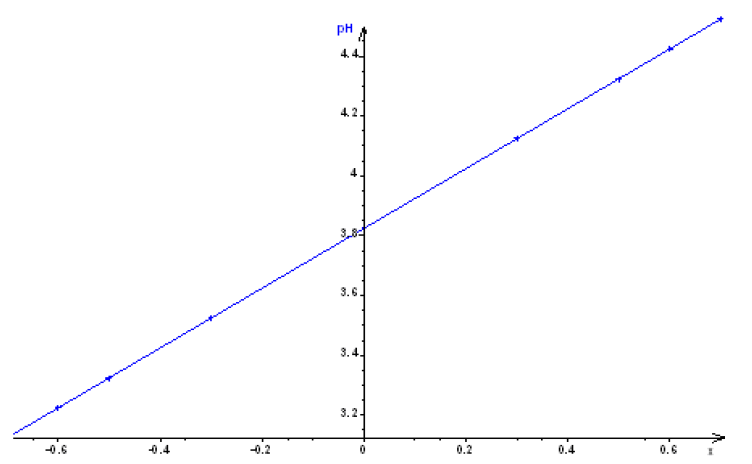
b) Le graphe représentant le $pH$ en fonction de $x$ est une fonction affine qui peut se mettre sous la forme : $pH=a+bx$
$a$ est l'ordonnée à l'origine :
$b$ est le coefficient directeur de la droite
$\begin{array}{lcl} b&=&\dfrac{\Delta pH}{\Delta x}\\&=&\dfrac{(4.5-3.1)}{(0.7-(-0.7))}\\&\Rightarrow&b=1\\&\Rightarrow&pH=3.8+\log x \end{array}$
2) Montrons que pour une même concentration d'acide et de base, $\dfrac{\left[RCOO^{-}\right]}{\left[RCOOH\right]}=\dfrac{V_{B}}{V_{A}}$
Dans le mélange :
$\left[RCOO^{-}\right]=\dfrac{CV_{B}}{V_{A}+V_{B}}$
$\begin{array}{lcl} \left[RCOO^{-}\right]&=&\dfrac{CV_{B}}{V_{A}+V_{B}}\\&\Rightarrow&\dfrac{\left[RCOO^{-}\right]}{\left[RCOOH\right]}\\&=&\dfrac{\dfrac{CV_{B}}{V_{A}+V_{B}}}{\dfrac{CV_{A}}{V_{A}+V_{B}}}\\&=&\dfrac{CV_{B}}{V_{A}+V_{B}}\times\dfrac{V_{A}+V_{B}}{CV_{A}}\\&\Rightarrow&\dfrac{\left[RCOO^{-}\right]}{\left[RCOOH\right]}=\dfrac{V_{B}}{V_{A}} \end{array}$
3) a) Expression du $pH$ du mélange obtenu en fonction du $pKa$ et du rapport : $\dfrac{\left[RCOO^{-}\right]}{\left[RCOOH\right]}$
Équation de la réaction :
$RCOOH\ +\ H_{2}O\ \rightarrow\ RCOO^{-}\ +\ H_{3}O^{+}$
La constante de réaction s'écrit :
$\begin{array}{lcl}K_{A}=\dfrac{\left[RCOO^{-}\right]\left[H_{3}O^{+}\right]}{\left[RCOOH\right]}\\&\Rightarrow&\log K_{A}=\log\dfrac{\left[RCOO^{-}\right]\left[H_{3}O^{+}\right]}{\left[RCOOH\right]}\\&=&\log\dfrac{\left[RCOO^{-}\right]}{\left[RCOOH\right]}+\log\left[H_{3}O^{+}\right]\\&\Rightarrow&-\log\left[H_{3}O^{+}\right]\\&=&-\log K_{A}+\log\dfrac{\left[RCOO^{-}\right]}{\left[RCOOH\right]}\\&\Rightarrow&pH=pK_{A}+\log\dfrac{\left[RCOO^{-}\right]}{\left[RCOOH\right]} \end{array}$
b) Le $pKa$ de l'acide
$pH=3.8+\log x=pH=3.8+\log\dfrac{\left[RCOO^{-}\right]}{\left[RCOOH\right]}$
et $pH=pK_{A}+\log\dfrac{\left[RCOO^{-}\right]}{\left[RCOOH\right]}$
Par identification :
$pK_{A}=3.8$
Exercice 10
1.1. Équation- bilan entre l'acide éthanoïque et l'eau
$CH_{3}COOH\ +\ H_{2}O\ \rightarrow\ CH_{3}COO^{-}\ +\ H_{3}O^{+}$
1.2.1. Expression du $pH$ et calcul du rapport $\dfrac{\left[CH_{3}COO^{-}\right]}{\left[CH_{3}COOH\right]}$
$\begin{array}{lcl} pH&=&pKa+\log\dfrac{\left[CH_{3}COO^{-}\right]}{\left[CH_{3}COOH\right]}\\&\Rightarrow&\dfrac{\left[CH_{3}COO^{-}\right]}{\left[CH_{3}COOH\right]}\\&=&10^{pH-pKa}\\&=&10^{3.4-4.78}\\&\Rightarrow&\dfrac{\left[CH_{3}COO^{-}\right]}{\left[CH_{3}COOH\right]}=4.2\cdot10^{-2} \end{array}$
1.2.2. Calcul des concentrations molaires des espèces chimiques présentes dans $S_{1}.$
Espèces chimiques présentes dans la solution $S_{1}$ :
$H_{3}O^{+}\;,\ CH_{3}COOH\;,\ CH_{3}COO^{-}\;,\ H_{2}O\;,\ OH^{-}$
$\begin{array}{lcl} \left[H_{3}O^{+}\right]&=&10^{-pH}\\&=&10^{-3.4}\\&\Rightarrow&\left[H_{3}O^{+}\right]=3.98\cdot 10^{-4}mol\cdot L^{-1} \end{array}$
$\begin{array}{lcl} \left[OH^{-}\right]&=&\dfrac{Ke}{\left[H_{3}O^{+}\right]}\\&=&\dfrac{10^{-14}}{3.98\cdot10^{-4}}\\&\Rightarrow&\left[OH^{-}\right]=2.5\cdot 10^{-11}mol\cdot L^{-1} \end{array}$
Electroneutralité de la solution : $\left[CH_{3}COO^{-}\right]+\left[OH^{-}\right]=\left[H_{3}O^{+}\right]$ solution acide, on néglige les ions $\left[OH^{-}\right]\Rightarrow\left[CH_{3}COO^{-}\right]=\left[H_{3}O^{+}\right]=3.98\cdot10^{-4}mol\cdot L^{-1}$
$\begin{array}{lcl}\left[CH_{3}COOH\right]&=&\dfrac{\left[CH_{3}COO^{-}\right]}{4.2\cdot10^{-2}}\\&=&\dfrac{3.98\cdot10^{-4}}{4.2\cdot10^{-2}}\\&\Rightarrow&\left[CH_{3}COOH\right]=9.5\cdot10^{-3}mol\cdot L^{-1}\end{array}$
1.2.3. Concentration $C_{A}$ de la solution $S_{1}$
La concentration de la matière s'écrit :
$\left[CH_{3}COOH\right]+\left[CH_{3}COO^{-}\right]=C_{A}$
la dissociation de l'acide étant faible $\Rightarrow C_{A}\approx\left[CH_{3}COOH\right]=9.5\cdot10^{-3}mol\cdot L^{-1}$
1.2.4. Détermination de la masse $m$ introduite
$\begin{array}{lcl} m&=&n\times M\\&=&C_{A}V\times M\\&=&9.5\cdot10^{-3}\times 1\times(12\times2+4\times1+16\times2)\\&\Rightarrow&m=0.75\,g \end{array}$
2.1. Les espèces chimiques présentes dans $S_{2}$ :
$H_{3}O^{+}\;,\ CH_{3}COOH\;,\ CH_{3}CO^{-}\;,\ H_{2}O\;,\ OH^{-}$
$\begin{array}{lcl} \left[H_{3}O^{+}\right]&=&10^{-pH}\\&=&10^{-8.4}\\&\Rightarrow&\left[H_{3}O^{+}\right]=3.98\cdot10^{-9}mol\cdot L^{-1} \end{array}$
$\begin{array}{lcl} \left[OH^{-}\right]&=&\dfrac{Ke}{\left[H_{3}O^{+}\right]}\\&=&\dfrac{10^{-14}}{3.98\cdot 10^{-9}}\\&\Rightarrow&\left[OH^{-}\right]=2.5\cdot 10^{-6}mol\cdot L^{-1} \end{array}$
$\left[Na^{+}\right]=C_{B}=10^{-2}mol\cdot L^{-1}$
Electroneutralité de la solution :
$\left[CH_{3}COO^{-}\right]+\left[OH^{-}\right]=\left[H_{3}O^{+}\right]+\left[Na^{+}\right]$,
on néglige les concentrations des ions $H_{3}O^{+}$ et $OH^{-}$ devant celle des ions $Na^{+}$
$\Rightarrow\left[CH_{3}COO^{-}\right]\approx\left[Na^{+}\right]=C_{B}=10^{-2}mol\cdot L^{-1}$
La concentration de la matière s'écrit :
$\begin{array}{lcl} \left[CH_{3}COOH\right]+\left[CH_{3}COO^{-}\right]&=&C_{B}\\&\Rightarrow&\left[CH_{3}COOH\right]&=&C_{B}-\left[CH_{3}COO^{-}\right]\\&\approx&0mol\cdot L^{-1} \end{array}$
2.3. Calcul de la valeur $pKa$ du couple acide/base
$\begin{array}{lcl} pH&=&\dfrac{1}{2}\left(14+pK_{A}+\log\,C_{B}\right)\\&\Rightarrow&pK_{A}=2pH-14-\log\,C_{B}\\&\Rightarrow&pK_{A}=2\times 8.4-14-\log\,10^{-2}\\&\Rightarrow&pK_{A}=4.8 \end{array}$
Les valeurs de $pKa$ sont équivalentes
3.1. Montrons que :
$\left[CH_{3}COOH\right]=\left[CH_{3}COO^{-}\right]$
Electroneutralité de la solution :
$\left[CH_{3}COO^{-}\right]+\left[OH^{-}\right]=\left[H_{3}O^{+}\right]+\left[Na^{+}\right]$
on néglige les concentrations des ions $H_{3}O^{+}$ et $OH^{-}$ devant celle des ions $Na^{+}$
$\begin{array}{lcl} \Rightarrow\left[CH_{3}COO^{-}\right]&\approx&\left[Na^{+}\right]\\&=&\dfrac{C_{B}V_{B}}{V_{A}+V_{B}}\\&=&\dfrac{10^{-2}\times 20}{20+20}\\&=&5\cdot 10^{-3}mol\cdot L^{-1} \end{array}$
$\begin{array}{lcl} \left[CH_{3}COOH\right]&=&\dfrac{10^{-2}\times V_{A}}{V_{A}+V_{B}}\\&=&\dfrac{10^{-2}\times 20}{30+20}\\&=&5\cdot 10^{-3}mol\cdot L^{-1}\\&\Rightarrow&\left[CH_{3}COOH\right]=\left[CH_{3}COO^{-}\right] \end{array}$
3.2. $pH$ de la solution $S$
$pH=pKa+\log\dfrac{\left[CH_{3}COO^{-}\right]}{\left[CH_{3}COOH\right]}$
or $\left[CH_{3}COOH\right]=\left[CH_{3}COO^{-}\right]$
$\Rightarrow\,pH=pKa=4.75$
3.3. Nom et propriétés de la solution
La solution est une solution tampon et, le $pH$ varie peu lors de l'addition modérée d'un acide fort ou d'une base forte ; ou lors d'une dilution.
Exercice 11
1.1 Détermination du volume $V_{0}$ de la solution commerciale
Le nombre de moles de l'acide ne varie pas :
$C_{0}V_{0}=C_{a}V_{a}$
$\Rightarrow\,V_{0}=\dfrac{C_{a}V_{a}}{C_{0}}$ or
$\begin{array}{lcl} C_{0}&=&\dfrac{m}{MV_{S}}\\&=&\dfrac{99\%m_{S}}{MV_{S}}\\&=&\dfrac{99\%\rho\,V_{S}}{MV_{S}}\\&=&\dfrac{99\%\rho}{M}\\&\Rightarrow&V_{0}=\dfrac{C_{a}V_{a}}{\dfrac{99\%\rho}{M}}\\&=&\dfrac{C_{a}V_{a}M}{99\%\rho}\\&=&\dfrac{0.1\times 1\times 60}{0.99\times 1050}\\&\Rightarrow&V_{0}=5.8\,mL \end{array}$
1.2 Équation bilan de la réaction de l'acide éthanoïque avec l'eau
$CH_{3}COOH+H_{2}O\ \rightarrow\ CH_{3}COO^{-}+H_{3}O^{+}$
2.1. Détermination de la masse $m_{b}$ d'éthanoate de sodium
$m_{B}=C_{b}V_{b}\times M=0.3\times 500\cdot 10^{-3}\times 82$
$\Rightarrow\,m_{b}=12.3\,g$
2.2. Équation de la dissociation de l'éthanoate de sodium dans l'eau
$CH_{3}COONa\ \rightarrow\ CH_{3}COO^{-}+Na^{+}$
2.3. Équation de la réaction entre un ion éthanoate et l'eau
$CH_{3}COO^{-}+H_{2}O\ \rightarrow\ CH_{3}COOH+OH^{-}$
3.1. Propriétés d'une solution tampon
Le $pH$ varie peu lors de l'addition modérée d'un acide fort ou d'une base forte ; ou lors d'une dilution
3.2. Expression de la constante d'acidité $Ka$ du couple d'acide éthanoïque ion/éthanoate
$Ka=\dfrac{\left[CH_{3}COO^{-}\right]\left[H_{3}O^{+}\right]}{\left[CH_{3}COOH\right]}$
$\begin{array}{lcl} \log\,Ka&=&\log\dfrac{\left[CH_{3}COO^{-}\right]\left[H_{3}O^{+}\right]}{\left[CH_{3}COOH\right]}\\&\Rightarrow&\log\,Ka=\log\dfrac{\left[CH_{3}COO^{-}\right]}{\left[CH_{3}COOH\right]}+\log\left[H_{3}O^{+}\right]\\&\Rightarrow&-pKa=-pH+\log\dfrac{\left[CH_{3}COO^{-}\right]}{\left[CH_{3}COOH\right]}\\&\Rightarrow&pH=pKa+\log\dfrac{\left[CH_{3}COO^{-}\right]}{\left[CH_{3}COOH\right]} \end{array}$
3.3. $pH=pKa$ lorsque $\left[CH_{3}COOH\right]=\left[CH_{3}COO^{-}\right]$
3.4. Détermination les volumes d'acide éthanoïque et d'éthanoate de sodium à utiliser
$\left[CH_{3}COOH\right]=\dfrac{C_{a}V_{a}}{V_{a}+V_{b}}$ ;
$\left[CH_{3}COOH\right]=\dfrac{C_{b}V_{b}}{V_{a}+V_{b}}$ ;
$\left[CH_{3}COOH\right]=\left[CH_{3}COO^{-}\right]$
$\begin{array}{lcl} \left[CH_{3}COOH\right]&=&\left[CH_{3}COO^{-}\right]\\&\Rightarrow&\dfrac{C_{a}V_{a}}{V_{a}+V_{b}}=\dfrac{C_{b}V_{b}}{V_{a}+V_{b}}\\&\Rightarrow&C_{a}V_{a}=C_{b}V_{b}\\&\Rightarrow&V_{a}=\dfrac{C_{b}}{C_{a}}V_{b}\text{ or }V_{a}+V_{b}=V\\&\Rightarrow&\dfrac{C_{b}}{C_{a}}V_{b}+V_{b}=V\\&\Rightarrow&V_{b}=\dfrac{V}{\dfrac{C_{b}}{C_{a}}}+1\\&=&\dfrac{100}{\dfrac{0.3}{0.1}}+1\\&\Rightarrow&V_{b}=25\,mL \end{array}$
$V_{a}=V-V_{b}=100-25\Rightarrow\,V_{a}=75\,mL$
4.1. Tracé de la courbe $pH=f\left(V_{b}\right)$
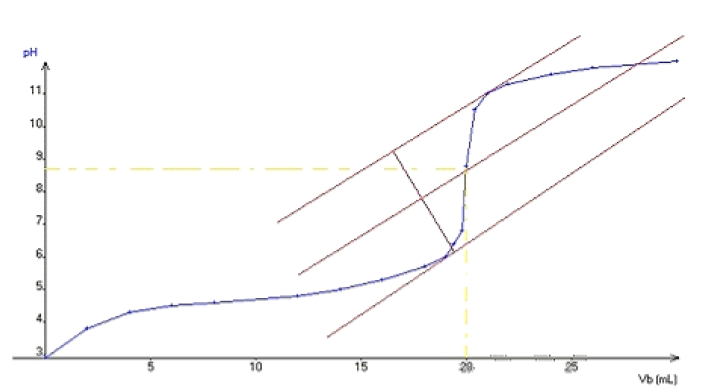
4.2. Détermination graphique des coordonnées du point d'équivalence $E$
A l'équivalence : $V_{E}=20\,mL\text{ et }pH_{E}=8.8$
4.3. Valeur de la concentration molaire $Ca$ de la solution d'acide éthanoïque
$\begin{array}{lcl}C_{a}V_{a}&=&C_{b}V_{E}\\&\Rightarrow&C_{a}=\dfrac{C_{b}V_{E}}{V_{a}}\\&=&\dfrac{0.1\times 20}{20}\\&\Rightarrow&C_{a}=0.1\,mol\cdot L^{-1} \end{array}$
4.4. Valeur du $pKa$ du couple $CH_{3}COOH|CH_{3}COO^{-}$
$pKa=4.75$

Commentaires
ahmed (non vérifié)
ven, 01/01/2021 - 11:49
Permalien
tres bon travail merci
ahmed (non vérifié)
jeu, 05/06/2021 - 17:06
Permalien
Tres bon travail
Anonyme (non vérifié)
lun, 03/11/2024 - 17:49
Permalien
Correction exo 12
Ajouter un commentaire