Exercices : géométrie dans l'espace 3e
Classe:
Troisième
Exercice 1
Une pyramide régulière à base carrée a pour hauteur $21\;cm$ ; son volume est de $847\;cm^{3}.$
a) Calcule le coté du carré de sa base.
b) Détermine la longueur $[AC]$.
c) Calcule la longueur des arêtes de la pyramide.
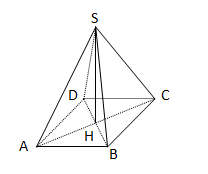
Exercice 2
Soit $SABCD$ une pyramide régulière à base carrée de hauteur $[SH]$.Faire la figure. On donne aire de base $50\;cm^{2}$ et une arête $[SA]$ $\ 13\;cm.$
1) Calculer la valeur exacte de $AB$, puis démontrer que $AC=10\;cm.$
2) Calcule $[SH]$ et le volume de $SABCD.$
Exercice 3
Une boîte de chocolats a la forme d'une pyramide tronquée (figure ci-dessous). Le rectangle $ABCD$ de centre $H$ et le rectangle $A'B'C'D'$ de centre $H'$ sont des plans parallèles. On donne : $AB=6\;cm\;;\ BC=18\;cm\;;\ HH'=8\;cm\;;\ SH=24\;cm.$
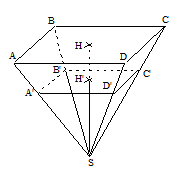
1) Calcule le volume $V_{1}$ de la pyramide $SABCD$ de hauteur $SH.$
2) Quel est le coefficient $k$ de la réduction qui permet de passer de la pyramide $SABCD$ à la pyramide $SA'B'C'D'$ de hauteur $SH'\; ?$
3) Déduis en le volume $V_{2}$ de la pyramide $SA'B'C'D'$ puis le volume $V_{3}$ de la boîte de chocolats ?
Exercice 4
$SABCD$ est une pyramide régulière dont la base est un carré de $240\;cm$ de coté.
1) On coupe cette pyramide par un plan parallèle à sa base. Le tronc de pyramide obtenu (la partie différente de la réduction) est un récipient de $30\;cm$ de profondeur et dont l'ouverture est un carré de $80\;cm$ de coté.
a) Montre que la hauteur de la pyramide initiale $SABCD$ est de $45\;cm$ et que celle de la pyramide réduite est $15\;cm.$
b) Calcule le volume de ce récipient.
2) Les faces latérales de ce récipient sont des trapèzes de mêmes dimensions.
a) Montre que la hauteur de ces trapèzes est $10\sqrt{73}\;cm$.
b) calcule l'aire latérale de ce récipient.
Exercice 5
$SABCD$ est une pyramide régulière dont la base est le carré $ABCD$ de côté $5\;cm$ et de centre $I.$ La hauteur $[SI]$ de la pyramide a pour longueur $SI=3\;cm.$
1) Calculer le volume de la pyramide.
2) Soit $M$ le milieu de l'arête $[BC]$.
Démontrer que la longueur $IM=2.5\;cm$.
3) On admet que le triangle $SIM$ est rectangle en $I$.
a) Calculer tan $MSI$
b) En déduire la mesure de l'angle $\widehat{MSI}$ à un degré prés
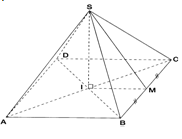
Exercice 6
$SABCD$ est une pyramide de hauteur $[OS]$. Son volume est de $240\;cm^{3}$ et sa hauteur $[OS]$ mesure $15\;cm$
1) A partir de la formule donnant le volume de la pyramide, calculer l'aire de la base $(ABCD).$
2) $O'$ est le point du segment $[SO]$ tel que $O'S=\dfrac{1}{2}OS.$
Le plan passant par $O'$ et parallèle à la base $(ABCD)$ coupe les droites $(SA)$ en $A'$ $\ (SB)$ en $B'$, $\ (SC)$ en $C'$ et $(SD)$ en $D'.$
Calculer le volume de la pyramide $(SA'B'C'D').$
3) On donne $OA=5\;cm$. calculer au degré près la mesure de l'angle $\widehat{OSA}.$
Exercice 7
Figure ci-dessous représente le patron de la partie latérale d'un cône de révolution.
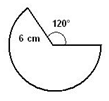
1) Montrer que le rayon de sa base est $4\;cm$ et que sa hauteur $h$ mesure $2\sqrt{5}\;cm$
2) Calculer son volume.
3) On coupe ce cône par un plan parallèle à sa base à $\dfrac{2}{3}$ de la hauteur à partir de la base. Calculer le volume du tronc.
Exercice 8
Le chapeau d'un berger a la forme d'un cône de révolution de sommet S (voir figure ci-dessous) : $IH=10\;cm\;,\ SH=10\;cm$. $\ H$ est le centre du disque de base.
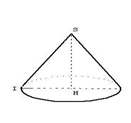
1) Calculer le volume de ce cône.
2) Le berger recouvre son chapeau extérieurement d'un papier de décoration vendu par feuille carrée de $10\;cm$ de coté et à 1000 F la feuille. Calculer la dépense minimale.
Exercice 9
On se propose de calculer le volume d'un seau qui a la forme d'un tronc de cône de révolution.
On donne $OS=2\sqrt{13}$ et $OA= 2a$. $\ a$ étant un nombre réel positif, et $O'$ milieu de $[OS].$
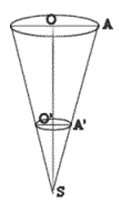
1) Calcule $O'A'$ en fonction de $a$.
2) On prend $a=\sqrt{3}$ pour la suite et pour unité le décimètre.
a) Calcule le volume du cône initial.
b) Calcule le volume du cône réduit et en déduire celui du seau.
Exercice 10
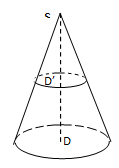
$C$ est un cône de sommet $S$ et de base un disque $D$ de rayon $5\;cm$. Le volume de ce cône est de $80\;cm^{3}$. Le disque $D'$ de rayon $3\;cm$ est une section du cône $C$ par un plan parallèle à la base. $C'$ est le cône de sommet $S$ et de base le disque $D'$. On se propose de calculer le volume de $C'.$
a) $D'$ est une réduction de $D$ ; à l'aide des rayons de $D$ et de $D'$, calcule l'échelle de cette réduction.
b) Quelle formule permet de calculer le volume de $C'$ à partir du volume de $C$ ? Calcule le volume de $C'.$
Exercice 11
Soit $SABCD$ une pyramide régulière à base carrée. Sa hauteur mesure $6\;cm$ ; le coté de sa base mesure $4\;cm.$
$O$ est le centre de la base.
1) Dessine la pyramide en perspective cavalière.
2) Calculer la longueur de ses arêtes latérales.
3) Dessine le patron de cette pyramide (échelle 1/2)
4) Calculer l'aire latérale et l'aire totale.
5) Calculer le volume de cette pyramide.
Exercice 12
$ABCD$ est un tétraèdre tel que : la base $ABC$ est rectangle en $A$ et de hauteur $[AD].$ On suppose que $AB=6\;cm\;;\ AC=8\;cm$ et $AD=8\;cm.$
1) Dessine ce tétraèdre en perspective cavalière.
2) Montrer que $BCD$ est un triangle isocèle en $B.$
3) Calculer le volume de ce tétraèdre.
4) Calculer l'aire totale de ce tétraèdre.
Exercice 13
L'unité de longueur est le cm. $ACBE$ est un losange tel que : $CE=12$ et $AB=6.$
1) Représente $ACBE$ en dimensions réelles.
2) S est un point n'appartenant pas au plan contenant ce losange tel que : $SABC$ soit un tétraèdre de hauteur $[SB]$ avec $SB=8.$
a) Calculer $SA$ et $SC$ (on remarquera que $(SB)\perp(BA)$ et $(SB)\perp(BC)).$
b) Calculer l'aire de $ACBE$ en déduire l'aire de $ABC.$
c) Calculer le volume du tétraèdre $SABC.$
Exercice 14
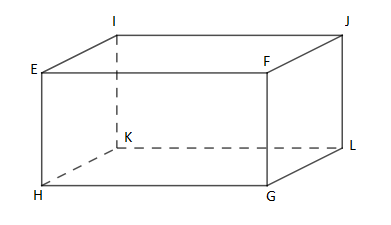
La figure ci-dessous $EFGHIJLK$ est un parallélépipédique rectangle tel que : $EF=8\;cm\;;\ EH=6\;cm$ et $HK=4\;cm.$
1) Calculer le volume du parallélépipède et l'aire totale.
2) Calculer $EG.$
3) Calculer l'aire du triangle $EGH.$
4) Calculer le volume de la pyramide de base $EGH$ de sommet $K.$
Exercice 15
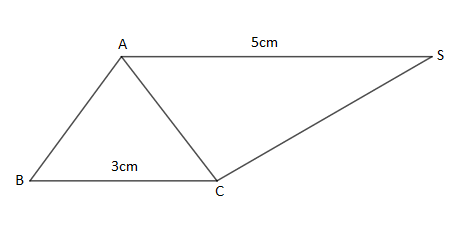
La figure ci-dessous est une partie d'un patron de la pyramide régulière $SABC.$
1) Terminer ce patron.
2) Calculer l'apothème de cette pyramide.
3) Calculer l'aire latérale et l'aire totale.
4) Calculer la hauteur et le volume.
Exercice 16
$SAB$ est un cône de révolution de sommet $S$ de centre $O$ et du diamètre de base le segment $[AB]$ tel que : $AB=4\;cm$ et $SO=8\;cm.$
1) Dessine ce cône en perspective cavalière.
2) Calculer la génératrice $[SA].$
3) Calculer le volume et l'aire totale du cône.
4) Calculer l'angle d'ouverture du développement de ce cône.
5) Représenter le patron de ce cône.
Exercice 17
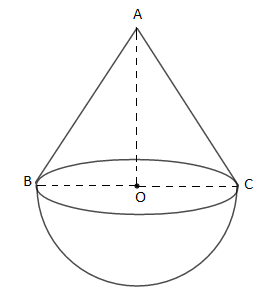
Une balise est formée d'une demi boule surmontée d'un cône de révolution comme l'indique la figure ci-dessous. On donne $AB=10\;cm$ et $BC=12\;cm.$
1) Calculer la distance $AO.$
2) Calculer le volume $V$ de la balise.
3) Calculer l'aire latérale $A_{\text{lat}}$ de la balise.
Exercice 18
Une pyramide de sommet $S$ et de base le trapèze $ABCD$ a pour hauteur $SA=8\;cm.$ On donne $AB=6\;cm\;;\ DC=4\;cm\ $ et $\ AD=3\;cm.$ Le trapèze est rectangle de bases $[AB]\ $ et $\ [DC].$
1) Calculer l'aire de ce trapèze.
2) Faire une figure de la pyramide.
3) Préciser la nature du triangle $SAB.$ Calculer $SB.$
4) Calculer le sinus de l'angle $\widehat{ABS}.$
5) Un plan $\mathcal{P}$ sectionne la pyramide $(ABCDS)$ parallèlement à sa base $(ABCD)$ à $1/3$ de sa hauteur $[SA]$ à partir de $A$ et coupe respectivement les arêtes $[SA]\;;\ [SB]\;;\ [SC]$ et $[SD]$ en $I\;,\ J\;,\ K$ et $L.$ Compléter la figure et préciser la nature de la section $(IJKL).$
6) Monter que $\dfrac{IJ}{AB}=\dfrac{2}{3}$ et en déduire $IJ.$
7) Calculer le volume de la pyramide $(IJKLS)$ et celui du tronc $(IJKLABCD).$
Exercice 19
Un entrepreneur des travaux publics doit aménager le long des allées d'une avenue des bancs en béton. Il hésite entre deux modèles :
Le modèle 1 a la forme d'un tronc de cône de révolution dont les bases parallèles ont respectivement $20\;cm$ et $10\;cm$ de rayons.
Le modèle 2 a la forme d'un tronc de pyramide dont les bases parallèles sont des carrées de cotés respectifs $40\;cm$ et $20\;cm.$
Les deux modèles ont une hauteur de $50\;cm.$
1) Représenter chaque modèle.
2) Sachant que le modèle le moins volumineux est le plus économique pour l'entrepreneur ; aidez le à faire le bon choix.
Exercice 20
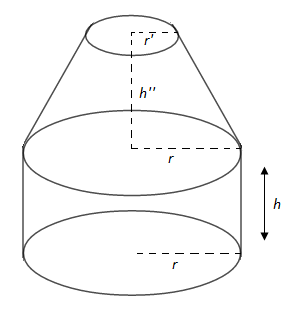
Un réservoir est constitué d'un cylindre de rayon de base $r$ et de hauteur $h$ et d'un cône de révolution de même rayon de base et de hauteur $h'=\dfrac{3h}{2}.$ (Voir la figure ci-dessous)
1) Montrer que le volume de cylindre est le double de celui du cône.
2) Dans la suite on donne $r=4\;cm.$
a) Calculer la hauteur $h'$ du cône pour que le volume du réservoir soit de $528\;cm^{3}.$
b) Pour créer une ouverture du réservoir on coupe le cône à mi-hauteur parallèlement au plan de sa base. On obtient un réservoir ayant la forme indiquée par la figure ci-dessous : Calculer le volume restant du réservoir.
On donne $\pi\cong\dfrac{22}{7}$

Exercice 21
On considère une pyramide de sommet $E$ et de base un carré $ABCD$ et de hauteur $[EA].$
On donne $EA=AB=5\;cm.$
1) Calculer la longueur $AC$ et en déduire la longueur $CE.$
2) Démontrer que le triangle $EBC$ est rectangle en $B.$
3) On coupe cette pyramide par un plan $\mathcal{P}_{1}$ parallèle à sa base à $\dfrac{1}{3}$ à partir de la base. Calculer le volume du tronc de pyramide obtenu.
4) Soit $\mathcal{C}_{1}$ le cercle circonscrit à la base $ABCD$ de la pyramide $EABCD.$ Déterminer son centre et son rayon.
5) On considère le cône de révolution de base $\mathcal{C}_{1}$, de sommet $F$ et de hauteur $[FO]$ telle que $FO=5\;cm.$ Calculer l'aire latérale de ce cône.
6) On coupe ce cône par un plan $\mathcal{P}_{2}$ parallèle à sa base à $\dfrac{2}{5}$ à partir du sommet. Calculer le volume du tronc de cône obtenu.
Exercice 22
Répondre par vraie ou fausse en justifiant la réponse
1) Un cône de révolution dont la hauteur mesure $10\;cm$ et dont le rayon de base mesure $6\;cm$ a un volume de $360\pi\;cm^{3}.$
2) Si on double l'arête d'un cube son volume est multiplié par 2.
Exercice 23
Recopie puis réponds par vrai ou faux :
1) Un tétraèdre est une pyramide qui a quatre faces.
2) La hauteur d'une pyramide est la droite qui relie son sommet au centre de sa base.
3) Une génératrice d'un cône de révolution est un segment qui relie le sommet du cône à un point du cercle de base.
4) Si une pyramide a sept faces, alors sa base est un hexagone.
5) La hauteur d'une pyramide passe toujours par le centre de la base.
6) Le patron d'un cône de révolution est constitué de $2$ disques pleins.
7) Dans un cône de révolution, la longueur d'une génératrice est le périmètre du disque de base.
Exercice 24
Reproduis la figure puis relie chaque phrase de la colonne $A$ à un nom de figure de la colonne $B.$
$$\begin{array}{|l|r|} \hline \text{Colonne }A&\text{Colonne }B\\ \hline\text{La section d'une pyramide à base carrée}&\text{hexagone}\\ \text{par un plan parallèle à la base est un}&\\ \hline\text{La section d'un tétraèdre régulier par un}&\text{carré}\\ \text{plan parallèle à la base est un}&\\ \hline\text{La section d'une pyramide à base}&\text{triangle}\\ \text{hexagonale par un plan parallèle à la}&\text{équilatéral}\\ \text{base est un}&\\ \hline \end{array}$$
Exercice 25
1) $ABCD$ est une pyramide dont la base est un triangle rectangle et isocèle en $C$ tel que :
$AB=2.5\;cm\text{ et }BC=3\;cm.$
(Voir figure ci-dessous)
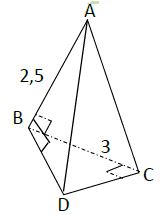
Construis le patron de cette pyramide.
2) Construis le patron d'un cône de révolution de rayon de base $3\;cm$ et de génératrice $5\;cm.$
Exercice 26
$EFGHLIJK$ est un parallélépipède rectangle tel que :
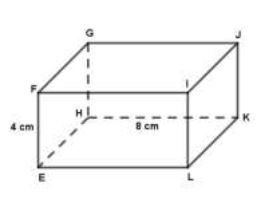
$EF=4\;cm$, $EH=4\;cm$ et $HK=8\;cm.$
1) Calcule le volume du parallélépipède.
2) Calcule $EG.$
3) Calcule l'aire du triangle $EGH.$
4) Calcule le volume de la pyramide de base $EGH$ et de sommet $L.$
5) Calcule l'aire totale de cette pyramide.
Exercice 27
La figure ci-dessous représente un tronc de cône dont les bases ont pour aires $12\;cm^{2}$ et $100\;cm^{2}.$

La distance $OO'$ des centres de bases est égale à $6\;cm.$
1) Calcule la hauteur puis le volume du cône.
2) Calcule le volume du tronc de cône.
Exercice 28
Le solide $A'B'C'D'ABCD$ est une caisse qui a la forme du tronc d'une pyramide régulière $SABCD$ à base carrée qui peut contenir $2024\;cm^{3}$ de mil.
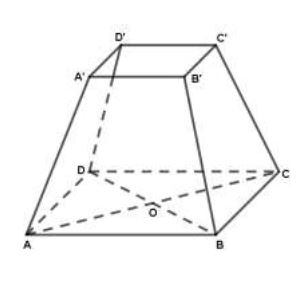
On donne :
$SA'=10\;cm$, $SO=28\;cm$, $AC=20\;cm$ et $AB=15\;cm.$
1) Que représente $[SA]$ pour la pyramide ?
2) Calcule sa longueur.
3) Calcule le volume de la pyramide $SABCD.$
Exercice 29
Cette médaille ci-dessous est tirée d'un patron d'une pyramide à base hexagonale.
On y voit $6$ faces qui sont des triangles équilatéraux superposables.
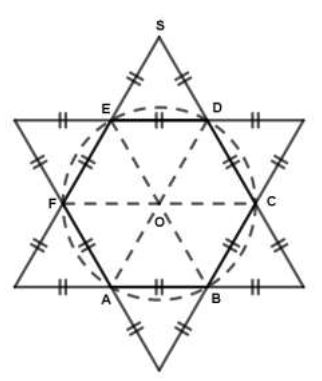
La hauteur de chaque triangle est de $4\sqrt{3}\;cm.$
Calcule :
1) l'arête de base de la pyramide ;
2) l'aire de base de la pyramide ;
3) sachant que la hauteur $SO$ de la pyramide vaut $6\;cm$, calcule le volume et l'aire latérale de la pyramide.
Exercice 30
Fatou mange de la glace ayant la forme d'un cône de révolution.
Au bout d'un moment, la hauteur de sa glace diminue de moitié.
Les figures ci-dessous schématisent la situation.
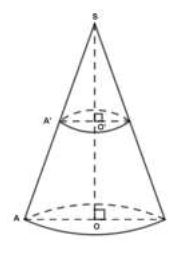
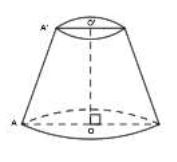
On donne :
$SA=15\;cm$ et $OA=2\;cm.$
On admet que les droites $(OA)$ et $(O'A')$ sont parallèles.
1) Dessine le triangle $SAO$ à l'échelle $\dfrac{1}{2}$ et calcule $O'A'.$
2) Calcule le volume de la glace que Fatou a mangé.
Quelle fraction du volume initial lui reste-t-il à manger ?
Exercice 31
On considère le tronc de cône ci-dessous associé à un cône de révolution de sommet $S$ et de rayon $OB=6\;cm.$
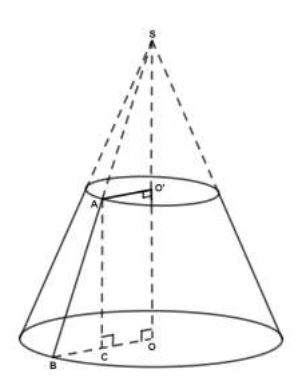
1) Sachant que $OO'=4\;cm$ ; $OB=6\;cm$ et $O'A=3\;cm$,
montre que :
$AB=5\;cm.$
2) Montre que la hauteur $SO$ de ce cône est égale à $8\;cm.$
3) La génératrice $SB$ de ce cône est égale à $10\;cm$ ;
calcule l'aire latérale $A_{L}$ du cône.
4) Ce cône de révolution est obtenu d'un secteur circulaire d'angle $\alpha.$
Calcule en degré la mesure de l'angle $\alpha$ du développement de ce cône.
5) Calcule le volume $V_{c}$ du cône initial.
Exercice 32
Le dessin ci-dessous représente un réservoir formé d'un tronc de cône de hauteur $6\;dm$ et de rayon de base (petite base) $4\;dm$ ; d'un cylindre de hauteur $8.5\;dm$ et de rayon $7\;dm.$
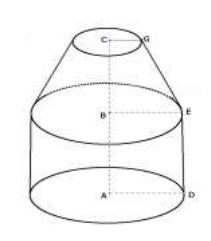
Calcule :
a) Le volume $V_{1}$ du tronc de cône ;
b) Le volume $V_{2}$ du cylindre et le volume total $V_{t}$ du réservoir.
Exercice de Synthèse
I. Le schéma ci-dessous représente le patron d'un cône de révolution de sommet $S$, de rayon de base $r.$
La génératrice $[SA]$ a pour longueur $36\;cm.$
1) Justifie que la circonférence de sa base mesure $54\pi\;cm.$
2) Montre que son rayon de base $r$ vaut $27\;cm.$
3) Justifie que la hauteur de ce cône est égale à $9\sqrt{7}\;cm$
4) Calcule l'aire totale de ce cône.
On prendra $\pi=3.14$
5) On sectionne ce cône et le rayon du cône réduit est égal à $15\;cm.$
Déterminer le coefficient de réduction ainsi que le volume du cône réduit

II. Soit un cône de révolution de sommet $S$ et dont la base est un disque de centre $O$ et de rayon $OA$ égal à $3\;cm$
1) Sachant que l'angle $OSA=30^{\circ}$ ; calculer la génératrice $SA$ de ce cône et montre que $SO=3\sqrt{3}$
2) Montre que le volume de ce cône de révolution est $9\pi\sqrt{3}\;cm^{3}$
3) On coupe ce cône par un plan parallèle à sa base de telle sorte que la base du cône réduit qui en résulte ait une aire de $\dfrac{9}{4}\pi\;cm^{2}.$
Calculer le coefficient de réduction $k$ et en déduire le volume $V'$ du cône réduit.
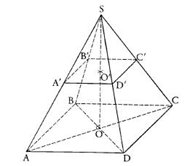
III. $SABCD$ est une pyramide à base carrée $ABCD$ de centre $H.$
On donne :
$AB=20\;cm$, $SA=40\;cm$, $SH$ est la hauteur et $A'$ est le milieu de $[SA].$
On coupe la pyramide par un plan parallèle à sa base passant par $A'.$
1) Calcule $AC$, $AH$ et $SH$
2) Soit $K$ milieu de $[AB]$, calculer $SK$
3) Calcule l'aire de base
4) Calcule le volume de la pyramide $SABCD.$
Déduis-en le volume $\mathcal{V'}$ de la pyramide réduite
VI. Dans cet exercice, les longueurs sont exprimées en $cm$
La relation entre la longueur $c$ du côté d'un carre et la longueur $d$ de sa diagonale est donnée par la formule $d=c\sqrt{2}.$
On donne $c=\sqrt{8}$
1) a) Montrer que la longueur de sa diagonale est un nombre entier.
b) Montrer que l'aire en $cm^{2}$ de ce carré est un nombre entier
2) La longueur de la diagonale d'un autre carré est $\sqrt{40}$
Calculer la longueur de son côté et exprimer cette longueur sous la forme $a\sqrt{5}$ où $a$ est un nombre entier naturel
V. Le volume d'un parallélépipède est égal :
a) $(L+l)\times h$
b) $(L-l)+h$
c) $L\times l\times h$

Commentaires
Anonyme (non vérifié)
sam, 05/25/2019 - 10:23
Permalien
Merci pour tout
Ndeye sokhna (non vérifié)
sam, 04/11/2020 - 22:53
Permalien
La correction de l’exercice
Anonyme (non vérifié)
lun, 05/31/2021 - 02:59
Permalien
La correction de l'exercice
Anonyme (non vérifié)
jeu, 04/29/2021 - 22:23
Permalien
Correction exercice 12 svp
Anonyme (non vérifié)
mer, 05/19/2021 - 22:51
Permalien
Correction de l'exercice 6
Anonyme (non vérifié)
lun, 05/31/2021 - 03:00
Permalien
Exo 32 correction
Dieynaba thiare (non vérifié)
lun, 04/29/2024 - 23:27
Permalien
Tétraèdre
Ajouter un commentaire