Organisation d'un calcul 6e
Classe:
Sixième
I. Règles de priorité des opérations
I.1 Priorité des parenthèses
Règles :
Les opérations entre parenthèses sont prioritaires sur toute autre opération.
Exemples :
$\begin{array}{rcl} A&=&3\times(4.5+7)\\ \\&=&3\times 11.5\\ \\&=&34.5\end{array}$
$\begin{array}{rcl} B&=&45\div(23-14)\\ \\&=&45\div 9\\ \\&=&5\end{array}$
$\begin{array}{rcl} C&=&35-(17+6)\\ \\&=&35-23\\ \\&=&12\end{array}$
$\begin{array}{rcl} D&=&(25\times 4)\div 5\\ \\&=&100\div 5\\ \\&=&20\end{array}$
I.2 Priorité de la multiplication par rapport à l'addition et à la soustraction
Règle :
La multiplication est prioritaire sur l'addition et la soustraction.
Exemples :
$\begin{array}{rcl} A&=&12+5\times 9\\ \\&=&12+45\\ \\&=&57\end{array}$
$\begin{array}{rcl} B&=&56-12\times 3\\ \\&=&56-36\\ \\&=&20\end{array}$
$\begin{array}{rcl} C&=&135\times 3-198\\ \\&=&405-198\\ \\&=&207\end{array}$
$\begin{array}{rcl} D&=&78\times 5+347\\ \\ &=&390+347\\ \\ &=&737\end{array}$
I.3 Priorité de la division par rapport à l'addition et à la soustraction
Règle :
La division est prioritaire sur l'addition et la soustraction.
Exemples :
$\begin{array}{rcl} A&=&45+78\div 2\\ \\&=&45+39\\ \\&=&84\end{array}$
$\begin{array}{rcl} B&=&678-790\div 10\\ \\&=&678-7.9\\ \\&=&670.1\end{array}$
$\begin{array}{rcl} C&=&575\div 25+68\\ \\ &=&23+68\\ \\&=&91\\ \end{array}$
$\begin{array}{rcl} D&=&956\div 4-173.67\\ \\&=&239-173.67\\ \\&=&65.33\end{array}$
II. Suite d'opérations
II.1 Suite de multiplication
Règle :
Dans une suite de multiplication ; on peut partir de la gauche vers la droite ou de la droite vers la gauche.
Exemple :
Calculer : $A=2.7\times 34\times 21.67\times 78\quad B=3468\div 6\div 16$
Solution
En partant de de la gauche vers la droite, on obtient :
$\begin{array}{rcl} A&=&2.7\times 34\times 21.67\times 78\\\\&=&91.8\times 21.67\times 78\\\\&=&1\,989.306\times 78\\\\&=&155\,165.868\end{array}$
En partant de de la droite vers la gauche, on obtient :
$\begin{array}{rcl} A&=&2.7\times 34\times 21.67\times 78\\\\&=&2.7\times 34\times 1\,690.26\\\\&=&2.7\times 54\,468.84\\\\&=&155\,165.868\end{array}$
D'où, $\boxed{A=155\,165.868}$
II.2 Suite de division
Règle :
Dans une suite de division ; on effectue les opérations de la gauche vers la droite.
Exemple :
Calculer : $B=3\,468\div 6\div 16$
Solution
On a :
$\begin{array}{rcl} B&=&3\,468\div 6\div 16\\\\&=&578\div 16\\\\&=&36.125\end{array}$
Donc, $\boxed{B=36.125}$
II.3 Suite d'addition
Règle :
Dans une suite d'addition ; on peut partir de la gauche vers la droite ou de la droite vers la gauche.
Exemple :
Calculer : $C=763+8\,745+233+338$
Solution
En partant de de la gauche vers la droite, on obtient :
$\begin{array}{rcl} C&=&763+8745+233+338\\\\&=&9\,508+233+338\\\\&=&9\,741+338\\\\&=&10\,079\end{array}$
En partant de de la droite vers la gauche, on obtient :
$\begin{array}{rcl} C&=&763+8\,745+233+338\\\\&=&763+8\,745+571\\\\&=&763+9\,316\\\\&=&10\,079\end{array}$
Ainsi, $\boxed{C=10\,079}$
II.4 Suite de soustraction
Règle :
Dans une suite de soustraction; on effectue les opérations de la gauche vers la droite.
Exemple :
Calculer : $D=94\,648-536-122-936$
Solution
On a :
$\begin{array}{rcl} D&=&94\,648-536-122-936\\\\&=&94\,112-122-936\\\\&=&93\,990-936\\\\&=&93\,054\end{array}$
D'où, $\boxed{D=93\,054}$
II.5 Suites d'opérations
Règle :
Dans une suite d'opérations ; on effectue les calculs en respectant les règles de priorité des opérations.
Ainsi, on effectue d'abord les opérations entre parenthèses ensuite, les multiplications et les divisions et enfin, les additions et les soustractions.
Exemples :
Calculer :
$$E=576+36\times(127.67-25)+4\,568\div 64\quad F=92\,354-54\times 4+45\div 9$$
Solution
On a :
$\begin{array}{rcl} E&=&576+36\times(127.67-25)+4\,568\div 64\\\\&=&576+36\times 102.67+4\,568\div 64\\\\&=&576+3\,696.12+71.375\\\\&=&4\,272.12+71.375\\\\&=&4\,343.495\end{array}$
D'où, $\boxed{E=4\,343.495}$
Soit :
$\begin{array}{rcl} F&=&92\,354-54\times 4+45\div 9\\\\&=&92\,354-54\times 4+5\\\\&=&92\,354-216+5\\\\&=&92\,138+5\\\\&=&92\,143\end{array}$
Ainsi, $\boxed{F=92\,143}$
Exercice d'application
Effectuer les opérations suivantes :
1) $3.3+4.5\times 6-13.5$
2) $4\times 7-8.3\div 2$
3) $42-(13+4\times 8.8)$
4) $(45+32)-3\times(19.3-4\times 2.3)\times 2$
Solution
1) On a :
$\begin{array}{rcl} 3.3+4.5\times 6-13.5&=&3.3+27-13.5\\ \\&=&30.3-13.5\\ \\&=&16.8\end{array}$
Ainsi, $\boxed{3.3+4.5\times 6-13.5=16.8}$
2) Soit :
$\begin{array}{rcl} 4\times 7-8.3\div 2&=&28-4.15\\ \\&=&23.85\end{array}$
Donc, $\boxed{4\times 7-8.3\div 2=23.85}$
3) On a :
$\begin{array}{rcl} 42-(13+4\times 8.8)&=&42-(13+35.2)\\ \\&=&42-48.2\\ \\&=&-6.2\end{array}$
D'où, $\boxed{42-(13+4\times 8.8)=-6.2}$
4) Soit :
$\begin{array}{rcl} (45+32)-3\times(19.3-4\times 2.3)\times 2&=&77-3\times(19.3-9.2)\times 2\\ \\&=&77-3\times 10.1\times 2\\ \\&=&77-60.6\\ \\&=&16.4\end{array}$
Alors, $\boxed{(45+32)-3\times(19.3-4\times 2.3)\times 2=16.4}$
III. Utilisation des parenthèses
Dans une suites d'opérations, pour éviter d'obtenir des résultats différents, on utilise des parenthèses et des crochets qui montrent les opérations prioritaires.
Exemple :
Calculer : $A=(84+(35.6-15.6)\times 32)\ $ et $\ B=((35\div 7)\times(354+56)$
Solution
On a :
$\begin{array}{rcl} A&=&84+((35.6-15.6)\times 32)\\\\&=&84+(20\times 32)\\\\&=&84+640\\\\&=&724\end{array}$
Ainsi, $\boxed{A=724}$
Soit :
$\begin{array}{rcl} B&=&((35\div 7)\times(354+56)\\\\&=&5\times 410\\\\&=&2\,050\end{array}$
Alors, $\boxed{B=2\,050}$
Remarque :
Si le calcul contient plusieurs parenthèses alors, on commence toujours par les parenthèses qui sont les plus intérieures. Ce qui permet de réduire petit à petit le nombre de parenthèses.
Exemple :
Calculer : $C=[((15+(12-7)+5)+(3\times 6))\times 2]+[((72\div 2)-(25+3))\div 4]$
Solution
On a :
$\begin{array}{rcl} C&=&[((15+(12-7)+5)+(3\times 6))\times 2]+[((72\div 2)-(25+3))\div 4]\\\\&=&[((15+5+5)+18)\times 2]+[(36-28)\div 4]\\\\&=&[(25+18)\times 2]+[8\div 4]\\\\&=&[43\times 2]+2\\\\&=&86+2\\\\&=&88\end{array}$
Ainsi, $\boxed{C=88}$
IV. Schéma de calcul
IV.1 Écriture en ligne
Dans une écriture en ligne, on traduit un énoncé mathématique sous forme de calcul en ligne ou suite d'opérations.
Exemple :
Traduis la différence de $250$ du produit de $6$ par la somme de $3\ $ et $\ 5$ sous la forme d'un calcul en ligne.
On obtient alors : $250-6\times(3+5)$
IV.2 Schéma de calcul
C'est un programme de calcul représenté sous forme de schéma et qui permet d'obtenir le résultat d'un calcul en ligne.
Exemple :
Calculer l'expression suivante, en utilisant un schéma de calcul :
$$A=[13+5\div 2-(14-13)+12\times 3]$$
Solution
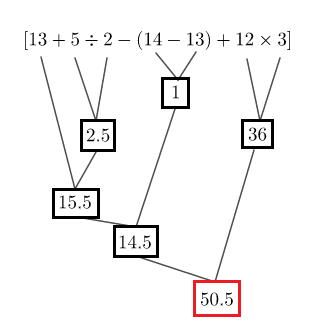
$\text{schéma de calcul}$
D'où, $\boxed{A=50.5}$

Commentaires
Ami (non vérifié)
ven, 08/14/2020 - 14:26
Permalien
Groupe
Ami (non vérifié)
ven, 08/14/2020 - 14:27
Permalien
Est ce que c'est un groupe
Anonyme (non vérifié)
jeu, 08/20/2020 - 21:32
Permalien
Super
Anonyme (non vérifié)
jeu, 08/20/2020 - 21:32
Permalien
Super
Anonyme (non vérifié)
jeu, 06/03/2021 - 19:49
Permalien
le I.1 vous avez fais une
Anonyme (non vérifié)
jeu, 06/03/2021 - 19:49
Permalien
le I.1 vous avez fais une
Anonyme (non vérifié)
jeu, 06/03/2021 - 19:49
Permalien
le I.1 vous avez fais une
Anonyme (non vérifié)
ven, 03/17/2023 - 21:34
Permalien
C'est exceptionnel.Machallah
Ajouter un commentaire