Vous êtes ici

Exercices : Statistique 3e

Classe:

Troisième

Exercice 1 BFEM 1994

Voici les tailles en cm des vingt élèves d'une classe de 3iéme. $$\begin{array}{cccccccccc} 165&145&150&166&165&160&158&162&165&150 \\ 158&165&154&158&160&162&162&154&165&160\end{array}$$

1) a) Quelle est la population étudiée ?

b) Quelle est le caractère étudié ? Puis donner sa nature.

2) Dresser le tableau des : Effectifs ; $\text{E.C.C ; E.C.D}$ ; Fréquences ; $\text{F.C.C}\ $ et $\ \text{F.C.D}$ en $\%.$

3) a) Combien d'élèves ont au plus $158\;cm\ ?$

b) Combien d'élèves ont plus de $158\;cm\ ?$

4) a) Quel est le mode de cette série ? Donner sa signification.

b) Calculer la taille moyenne de cette série. Donner sa signification.

Exercice 2 BFEM BLANC 2005

Le tableau ci-dessous représente les tailles de $40$ élèves d'une classe de $3^{\text{ième}}.$

$$\begin{array}{|c|c|c|c|c|c|}\hline\text{Tailles en}&[140\;;\ 150[&[150\;;\ 160[&[160\;;\ 170[&[170\;;\ 180[&[180\;;\ 190[ \\ cm& & & & & \\ \hline\text{Effectifs}& &8&5&18& \\ \hline\text{Fréquences}& & & & & \\ \text{en }\%& & & & & \\ \hline\text{F.C.C en }\%& & & & & \\ \hline\text{F.C.D en }\%& & & & & \\ \hline\end{array}$$

1) Compléter le tableau sachant que l'effectif de la classe $[140\;;\ 150[$ est la moitié de $[180\;;\ 190[.$

2) Quel est le pourcentage d'élèves dont la taille est inférieure à $1.80\;m$ et supérieure à $150\;cm\ ?$

3) Combien d'élèves ont une taille au moins égale à $160\;cm\ ?$

4) Quelle est la classe médiane de cette série ?

5) Combien d'élève ont une taille supérieure à la taille moyenne ?

6) Construire les histogrammes cumulatifs dans un même repère.

7) Faire apparaître les polygones ; déterminer graphiquement la médiane puis interpréter le résultat.

Exercice 3 BFEM 2006

Pour préparer une "opération Tabaski", un éleveur pèse ses $30$ moutons afin de les répartir par catégories de poids, en quatre classes de poids, d'amplitude $4\;kg$, qu'il désigne respectivement par : "4e choix" ; "3e

choix" ; "2e choix" ; "1e choix".

Le relevé ci-dessous donne le poids en kilogramme des moutons pesés : $$\begin{array}{cccccccccc} 50&52&52.5&54.5&52&59&58&55&55.5&56 \\ 55&55&57&58&58.5&60&60.5&65&63&60 \\ 61&65&64&65&55&59&58&59&59.5&65\end{array}$$

1) Donner les classes de cette répartition sachant que la borne inférieure de la première classe de poids est $50.$

2) Dresser le tableau des effectifs de la série groupée en classes obtenue. Déterminer la classe médiane.

3) On suppose dans la suite que le tableau des effectifs obtenu est : $$\begin{array}{|c|c|c|c|c|}\hline&\text{"4e choix"}&\text{"3e choix"}&\text{"2e choix"}&\text{"1e choix"} \\ \hline\text{Classes}&[50\;;\ 54[&[54\;;\ 58[&[58\;;\ 62[&[62\;;\ 66[ \\ \hline\text{Nombre de moutons :}&4&8&12&6 \\ \text{Effectifs}& & & & \\\hline\end{array}$$

Dessiner le diagramme circulaire de cette série.

4) Un mouton "1er choix" est vendu à $70\,000\;F$ un mouton "2e choix" $65\,000\;F$ et un mouton "4e choix" $52\,000\;F$. A combien un mouton "3e choix" devra-t-il être vendu pour que le prix de vente moyen des moutons soit $62\,000\;F$ une fois que les moutons seront tous vendus aux prix indiqués.

Exercice 4 BFEM 2007

Le tableau ci-dessous donne la répartition des joueurs d'une équipe de football, selon la taille en $m$ : $$\begin{array}{|c|c|c|c|c|}\hline\text{Tailles}&[1.65\;;\ 1.75[&[1.75\;;\ 1.85[&[1.85\;;\ 1.95[&[1.95\;;\ 2.05[ \\ \hline\text{Effectifs}&6&15&20&9 \\ \hline\end{array}$$

1) Recopier puis compléter le tableau ci-dessous en y faisant figurer : $\text{E.C.D ; F}$ en $\%\ $ et $\ \text{F.C.C}.$

2) Combien de joueurs ont une taille au moins égale à $1.75\;m\ ?$

3) Donner la taille moyenne dans cette équipe en centimètre prés par défaut.

4) Indiquer la classe modale de cette série statistique.

Exercice 5 BFEM 2009

1e Partie :

Le tableau statistique ci-dessous donne la répartition de notes d'élèves obtenues lors d'un examen. $$\begin{array}{|l|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline\text{Notes}&2&3&4&5&6&7&8&9&10&11&12&13&14&15&16&17 \\ \hline\text{Effectifs}&2&1&1&2&3&2&4&6&7&6&5&3&2&3&2&1\\ \hline\text{E.C.C}&&&&&&&&&&&&&&&&\\ \hline\text{E.C.D}&&&&&&&&&&&&&&&&\\ \hline\text{F en }\%&&&&&&&&&&&&&&&&\\ \hline\text{F.C.C en }\%&&&&&&&&&&&&&&&&\\ \hline\end{array}$$

1) Compléter le tableau ci-dessus.

2) Que représente l'effectif de la modalité $6\ ?\ \text{E.C.C}$ de la modalité $8\ ?\ \text{E.C.D}$ de la modalité $5\ ?\ \text{F.C.C}$ de la modalité $16\ ?$

3) Déduire de ce tableau le pourcentage des élèves qui ont moins de $14.$

2e Partie :

On groupe les notes précédentes en classes d'amplitude $4$ dans le tableau ci-dessous. $$\begin{array}{|c|c|c|c|c|c|}\hline\text{Notes}&[0\;;\ 4[&[4\;;\ 8[&[8\;;\ 12[&[12\;;\ 16[&[16\;;\ 20[ \\ \hline\text{Effectifs}& & & & & \\ \hline\text{E.C.C}& & & & & \\ \hline\end{array}$$

1) Recopie et complète le tableau.

2) Calcule la moyenne des notes obtenues par ces élèves.

3) Construire l'histogramme des effectifs cumulés croissants.

Exercice 6 BFEM 2008

$$\begin{array}{|c|c|c|c|c|c|}\hline\text{Nombre de jours à l'hôtel} & 2 & 3 & 4 & 5 & 6 \\ \hline\text{Effectifs cumulés décroissants} & 180 & 90 & 50 & 20 & 15 \\ \hline\end{array}$$

Le tableau statistique ci-dessus est réalisé par la direction commerciale d'un hôtel qui a reçu des invités lors du dernier sommet de l'O.C.I organisé à Dakar.

1) Quelle est la population étudiée ?

2) Indique le caractère étudié et précise sa nature.

3) Détermine la médiane de cette série.

4) a) Calcule le pourcentage des invités qui ont passé au moins $3$ jours à l'hôtel.

b) Calcule le nombre d'invités qui ont passé moins de $4$ jours à l'hôtel.

c) Quel est le nombre d'invités qui ont passé plus de $4$ jours à l'hôtel.

5) Construis le diagramme circulaire des effectifs de cette série.

Exercice 7 BFEM 2003

Le tableau ci-dessous représente la répartition des notes de mathématiques lors d'un test de niveau où la note moyenne est $12.5$

$$\begin{array}{|c|c|c|c|c|c|c|}\hline\text{Notes sur }20 & 6 & 8 & 9 & 12 & 15 & x \\ \hline\text{Nombre d'élèves} & 6 & 9 & 15 & 9 & 15 & 18 \\ \hline\end{array}$$

1) Calculer $x$, la meilleure note attribuée lors de ce test.

2) Combien d'élèves ont une note au moins égale à $12\ ?$

3) Quel est le pourcentage des élèves qui ont au plus $15\ ?$

4) Déterminer la note médiane

Exercice 8 BFEM 1997

Sur une période donnée les recettes d'une essencerie se répartissent comme suit :

$$\begin{array}{|c|c|c|c|c|}\hline\text{Carburant}&\text{Essence ordinaire}&\text{Essence super}&\text{Gasoil}&\text{Mélange} \\ \hline\text{Pourcentage de}&30\%&25\%&40\%&5\% \\ \text{toutes les recettes}& & & & \\ \hline\end{array}$$

1) Représenter cette série par un diagramme semi-circulaire.

2) Sachant que l'essence ordinaire vendue a rapporté $126\,000$ francs et que $42$ litres de mélange ont été vendus, trouver :

a) La somme rapportée par le gasoil

b) Le prix du litre de mélange

Exercice 9

Une entreprise a effectué une étude sur l'âge de ses clients en les classant par tranche d'amplitude $5$ ans.

$$\begin{array}{|c|c|c|c|c|c|c|c|c|}\hline\text{Age} & [15;\ 20[ & [20;\ 25[ & [25;\ 30[ & [30;\ 35[ & [35;\ 40[ & [40;\ 45[ & [45;\ 50[ & [50;\ 55[ \\ \hline\text{Effectif} & 2 & 5 & 8 & x & 18 & 4 & 6 & 3 \\ \hline \end{array}$$

1) Sachant que l'étude a porté sur un échantillon de $55$ clients, déterminer l'effectif manquant.

2) Calculer l'âge moyen des clients, en utilisant le centre des intervalles.

3) Reproduire le tableau et compléter par la ligne des effectifs cumulés croissants

4) Représenter l'histogramme et le polygone des effectifs cumulés croissants.

5) Utiliser le polygone des effectifs cumulés croissants pour déterminer l'âge médian

Exercice 10

$20$ élèves sautent en hauteur. Les performances sont classées en intervalles d'amplitude $10\;cm$.
$$\begin{array}{|c|c|c|c|c|c|}\hline\text{Performance}&[100\;;\ 110[&[110\;;\ 120[&[120\;;\ 130[&[130\;;\ 140[&[140\;;\ 150[\\ \hline\text{Centre}&&&&&\\\hline \text{Effectifs}&X&4&8&Y&2 \\ \hline \end{array}$$

1) Compléter la ligne des centres et préciser la classe modale.

2) la moyenne de cette série est $126.5\;cm$. Déterminer $X\ $ et $\ Y$

3) a) Construire l'histogramme des effectifs cumulés décroissants

b) Déterminer graphiquement la performance médiane

Exercice 11 BFEM 1999

Dans le registre des consultations du dispensaire d'un village, on a relevé les cas du paludisme et on obtient le tableau suivant :
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline\text{Mois}&\text{Jan}&\text{Fév}&\text{Mars}&\text{Avril}&\text{Mai}&\text{Juin}&\text{Juil}&\text{Aout}&\text{Sept}&\text{Oct}&\text{Nov}&\text{Déc}\\ \hline\text{Nombre}&&&&&&&&&&&&\\ \text{de cas}&21&12&5&4&2&6&13&68&92&53&40&30\\ \text{Paludisme}&&&&&&&&&&&&\\ \hline\end{array}$$
1) Ajouter au tableau la ligne des effectifs cumulés croissants.

2) Tracer le diagramme en bâtons de cette série ($1\;cm$ représente $10$ malades).

3) Représenter graphiquement la courbe des effectifs cumulés croissants ($2\;cm$ représente $50$ malades) puis déterminer la période médiane (le mois) pendant laquelle $50\%$ des malades ont été consultés.

4) En moyenne combien y a-t-il de malades du paludisme par mois ?

5) Le paludisme est la maladie qui tue le plus au Sénégal.

Sachant que $10.5\%$ des malades paludisme sont décédés et qu'ils représentent $75\%$ de l'ensemble des cas de décès annuels du dispensaire, calculer :

a) Le nombre de décès de malades du paludisme.

b) Le nombre total annuel de malades décédés de ce dispensaire.

Exercice 12 BFEM 2002

Un conseil régional, voulant octroyer $50$ bourses aux meilleurs élèves des classes de Troisièmes de sa localité, organise un concours à cet effet.

Le montant de la bourse dépend de la note obtenue, laquelle varie de $0$ à $20.$ Ce montant est fixé au maximum à $30\,000\;F.$

Le tableau ci-dessous résulte de la représentation de la série par un diagramme circulaire.

$$\begin{array}{|c|c|c|c|c|c|}\hline\text{Notes obtenues}&[10\;;\ 12[&[12\;;\ 14[&[14\;;\ 16[&[16\;;\ 18[&[18\;;\ 20[ \\ \hline\text{Montant de}&&&&&\\ \text{la bourse}&10\,000&15\,000&20\,000&25\,000&30\,000\\ \text{(F CFA)}&&&&&\\ \hline\text{Angles (en degrés)}&108&93.5&\widehat{A}&50.4&36\\ \hline\end{array}$$

1) Calculer l'angle manquant $\widehat{A}$.

2) Calculer les effectifs associés aux différents intervalles.

3) Calculer la valeur moyenne des bourses attribuées.

4) a) Quel est le nombre d'élèves qui ont une note au moins égale à $12\ ?$ En déduire le pourcentage correspondant.

b) Quel est le nombre d'élèves qui ont une bourse au plus égale à $25\,000\;F\ ?$

5) a) Construire le polygone des fréquences cumulées croissantes (exprimer les fréquences en pourcentages)

b) Déterminer la note médiane (en utilisant le théorème de Thalès)

Exercice 13

On a relevé les notes obtenues par des candidats à un examen noté sur $100.$
$$\begin{array}{|c|c|c|c|c|c|c|c|c|}\hline\text{Notes}&20\text{ à }30&30\text{ à }40&40\text{ à }50&50\text{ à }60&60\text{ à }70&70\text{ à }80&80\text{ à }90&90\text{ à }100\\ \hline\text{Nombre}&&&&&&&&\\ \text{de}&3&6&9&12&18&6&3&3\\ \text{candidats}&&&&&&&&\\ \hline\end{array}$$

1) Combien de candidats ont composé à cet examen ?

2) Donner dans un même tableau les fréquences en $\%$, les fréquences cumulées croissantes et les fréquences cumulées décroissantes en $\%$

3) Représenter sur un même graphique le diagramme (polygone) des fréquences cumulées croissantes et décroissantes.

4) Ces deux courbes se coupent en un point $I$. Quelles sont les coordonnées de $I\; ?$

5) On note $M$ l'abscisse du point $I$. Quel est le pourcentage de candidats ayant obtenu une note supérieure à $M\; ?$ Que représente $M\; ?$

Exercice 14

Un professeur de mathématiques a noté un devoir sur 10 puis a consigné les notes dans le tableau suivant :

$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|}\hline\text{Notes} & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ \hline\text{Effectifs} & 0 & 2 & 4 & 2 & 3 & 6 & 7 & 2 & 3 & 2 & 1 \\ \hline\end{array}$$

1) Calculer l'effectif total des élèves ayant composé puis la moyenne des notes obtenues

2) Le professeur répartit ensuite les notes en $6$ classes de notes pour obtenir une série classée

a) Reprendre et compléter le tableau ci-dessous

$$\begin{array}{|c|c|c|c|c|c|c|}\hline\text{Classe de}&0\leq n<2&2\leq n<4&4\leq n<6&6\leq n<8&8\leq n<10&10\leq n<12 \\ \text{notes}& & & & & & \\\hline\text{Effectifs} & & & & & & \\ \hline\text{ECC} & & & & & & \\ \hline\end{array}$$

b) Représenter à l'aide d'un histogramme les effectifs cumulés croissants et tracer le polygone des effectifs cumulés croissants

c) Définir et déterminer la classe modale puis calculer la médiane en utilisant le théorème de Thalès

d) Combien d'élèves ont une note au moins égale à $8\ ?$

e) Quel est le pourcentage d'élèves qui ont moins de $6\ ?$

f) Que représente l'effectif cumulé croissant associé à la classe $6\leq n<8\ ?$

Exercice 15

Pour chacun des énoncés ci-dessous, $3$ réponses $R_{1}\;,\ R_{2}\;,\ R_{3}$ sont proposées.

Pour Chaque énoncé relève le numéro suivi de la réponse choisie.

On considère la série de notes d'élèves représentée ci-dessous

$$\begin{array}{|c|c|c|c|c|} \hline \text{Note}&1\text{ à }4&5\text{ à }9&10\text{ à }14&15\text{ à }20\\ \hline \text{Effectif}&0&9&10&6\\ \hline \end{array}$$

$$\begin{array}{|c|l|c|c|c|} \hline N^{\circ}&\text{Enoncé}&R_{1}&R_{2}&R_{3}\\ \hline 1&\text{le centre de la classe }[22\;;\ 30]\text{ est}&11&26&23.5\\ \hline 2&2\text{ a) Le pourcentage d'élèves dont les notes varient}\text{de }5\text{ à }9\text{ est :}&15\%&40.5\%&36\% \\&2\text{ b) La note moyenne de la série est}&11.52&10&6.25 \\ &2\text{ c) La classe modale de la série est :}&10&15\text{ à }20&10\text{ à }14\\ \hline \end{array}$$

Exercice 16

Détermine la médiane et les quartiles de la série :

$$1\;;\ 1\ ;\ 3\;;\ 5\;;\ 5\;;\ 6\;;\ 8\;;\ 8\;;\ 8\;;\ 10\;;\ 11$$

Exercice 17

Le tableau suivant donne la répartition des notes des élèves de $3^{\text{ème}}$ à un devoir de biologie.

$$\begin{array}{|c|c|c|c|c|c|} \hline \text{Classes}&[0\;;\ 4[&[4\;;\ 8[&[8\;;\ 12[&[12\;;\ 16[&[16\;;\ 20[\\ \hline \text{Effectifs}&3&5&9&7&4\\ \hline \end{array}$$

1) Détermine la classe modale et une approximation de la moyenne de la classe à ce devoir.

2) Calcule la médiane de cette série.

3) Construis l'histogramme des effectifs.

Exercice 18

1) A partir de l'histogramme ci-dessous, donne le tableau des effectifs par classe de la série statistique représentée

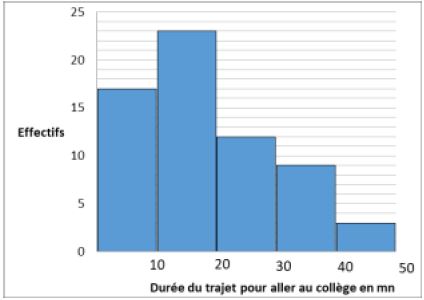
2) Calcule l'effectif total de cette série.

3) Détermine une approximation de la moyenne de cette série.

4) Détermine graphiquement la classe modale.

Exercice 19

La taille moyenne des onze joueurs d'une équipe de football est de $1.81$ mètre.

On a pu relever la taille, en mètre, des dix joueurs sauf celle du gardien de but :

$$1.71\;-\;1.80\;-\;1.85\;-\;1.75\;-\;1.78\;-\;1.83\;-\;1.75\;-\;1.80\;-\;1.85\;-\;1.90$$

1) Détermine la taille du gardien.

2) Détermine la taille médiane de ces onze joueurs.

3) Dans cette équipe, il y a trois remplaçants de la même taille.

La moyenne de la taille de ces quatorze joueurs est alors de $1.84$ mètre.

4) Détermine la taille de chacun des trois remplaçants.

5) Détermine la taille médiane de cette nouvelle série.

Exercice 20

Une enquête a été réalisée dans une bibliothèque pour étudier le nombre de livres lus par les usagers, en décembre $2015.$

Le diagramme en bâtons ci-dessous donne la fréquence associée à chaque nombre de livres lus.

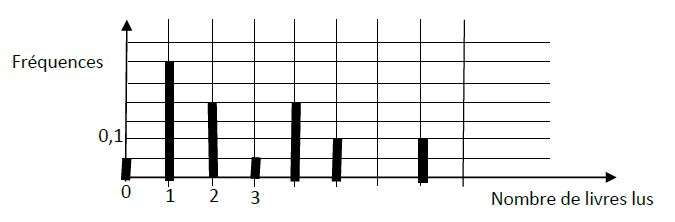
1) Détermine graphiquement le nombre médian de livres lus.

Explique ta démarche.

2) Calcule le nombre moyen de livres lus par les usagers de cette bibliothèque en décembre $2015.$

Exercice 21

Reproduis puis réponds par Vrai ou Faux à chacune des affirmations ci-dessous.

$$\begin{array}{|l|c|} \hline \text{Affirmations}&\text{Réponses}\\ \hline \text{1) La médiane d'une série statistique est forcément une des valeurs de la série.}&\\ \hline \text{2) Dans un regroupement par classe, une valeur peut appartenir à deux classes}&\\ \text{différentes.}&\\ \hline \text{3) Dans une série statistique, la moitié des données ont une valeur inférieure à la}&\\ \text{moyenne.}&\\ \hline \end{array}$$

Exercice 22

La distribution des salaires mensuels des $530$ ouvriers d'une entreprise est représentée par le tableau ci-dessous.

$$\begin{array}{|c|c|c|c|c|c|c|}\hline \text{Salaires}&&&&&&\\ \text{en}&[45\,000\;;\ 47\,000[&[47\,000\;;\ 49\,000[&[49\,000\;;\ 51\,000[&[51\,000\;;\ 53\,000[&[53\,000\;;\ 55\,000[&[55\,000\;;\ 57\,000[\\\text{F CFA}&&&&&&\\ \hline\text{Effectifs}&&&&&&\\ \hline \text{Effectifs}&&&&&&\\ \text{cumulés}&&&&&&\\\text{croissants}&&&&&&\\ \hline\text{Fréquence en }\%&&&&&&\\ \hline\text{Angles}&&&&&&\\ \text{correspondant}&17^{\circ}&75^{\circ}&122^{\circ}&85^{\circ}&34^{\circ}&27^{\circ}\\ \text{aux fréquences}&&&&&&\\ \hline \end{array}$$

1) Reproduis et complète le tableau ci-dessus.

2) Quel est le nombre d'ouvriers ayant un salaire strictement inférieur à $51\,000\;F\ ?$

3) Calcule le salaire moyen de cette entreprise.

Exercice 23

On a réparti $100$ personnes selon leur temps de sieste exprimé en minutes $(mn).$

$$\begin{array}{|c|c|c|c|c|c|} \hline \text{Classes}&[30\;;\ 50[&[50\;;\ 70[&[70\;;\ 90[&[90\;;\ 110[&[110\;;\ 130[\\ \hline \text{Effectifs}&10&20&x&40&y\\ \hline \end{array}$$

Le temps moyen de sieste est de $82\;mn.$

1) Reproduis puis complète le tableau ci-dessus en mettant les centres de classes.

2) En exprimant l'effectif total et la moyenne en fonction de $x\ $ et $\ y$, montre que $x\ $ et $\ y$ vérifient le système suivant :

$$\left\lbrace\begin{array}{lcl} x+y&=&30\\ \\2x+3y&=&65 \end{array}\right.$$

3) Pour la suite, on donne $x=25\ $ et $\ y=5.$

a) Reprends le tableau ci-dessus en indiquant les fréquences (en $\%$) et les fréquences cumulées croissantes (en $\%$).

b) Détermine pourcentage de personnes qui ont un temps de sieste au moins égal à $70\;mn.$

4) Trace l'histogramme et le polygone des fréquences cumulées croissantes (en $\%$).

($1\;cm$ pour $10$ sur l'axe des abscisses et $1\;cm$ pour $10$ sur l'axe des ordonnées).

5) A l'aide du théorème de Thalès, détermine le temps médian de sieste.

Exercice de synthèse

I. Les notes des $160$ candidats à un concours sont consignées dans le tableau suivant

$$\begin{array}{|c|c|c|c|c|c|} \hline \text{Notes}&[10\;;\ 12[&[12\;;\ 14[&[14\;;\ 16[&[16\;;\ 18[&[18\;;\ 20[\\ \hline \text{Nombres}&48&40&x&24&y\\ \text{De candidats}& & & & &\\ \hline \end{array}$$

La moyenne de cette série statistique est égale à $14$ et la somme de $x\ $ et $\ y$ est égale à $48$

1) Quel est le caractère étudié ?

Déterminer sa nature.

2) Calculer et placer dans le tableau, le centre de chaque classe.

3) Déterminer $x\ $ et $\ y$

4) Calculer le pourcentage des candidats ayant une note comprise entre $[14\;;\ 16[$

5) Dresser le tableau des $\text{E.C.C}\ $ et $\ \text{E.C.D}$ puis construire le diagramme des $\text{E.C.C}\ $ et $\ \text{E.C.D}.$

6) Déterminer graphiquement la médiane.

7) Déterminer la classe modale.

II. Le tableau suivant donne les angles de la répartition des catégories socioprofessionnelles des femmes en milliers.

Le nombre de femmes total des catégories est de $100\;\text{milliers}$

$$\begin{array}{|c|c|c|c|c|c|} \hline \text{Catégories}&\text{Cadres}&\text{Cadres}&\text{Employés}&\text{Ouvriers}&\text{Personnel de}\\ \text{socioprofessionnelles}& \text{supérieurs}&\text{moyens}& & &\text{service}\\ \hline \text{Angles}&90&54&72&108&36\\ \hline \end{array}$$

1) Construire le diagramme en secteur de la répartition des catégories socioprofessionnelles.

2) Calculer le nombre de femmes de chaque catégorie socioprofessionnelle.

3) Dresser le tableau des fréquences cumulées croissantes.

4) Quelles sont les modalités

5) Quel est le caractère observe ?

Quel est la nature du caractère ?

6) Quelles représentations graphiques peut-on envisager ?

Représenter le diagramme envisagé.

7) Déterminer la médiane.

III. La moyenne arithmétique d'une série statistique d'un caractère quantitatif continue est égale :

a) $\dfrac{1}{n}\sum\;n_{i}x_{i}$ b) $\dfrac{1}{n}\sum\;n_{i}$ c) $\dfrac{1}{n}\sum\;x_{i}$