Corrigé BFEM Physique chimie 2012
Exercice 1
1) Calculons le nombre de moles d'acide et de base.
$-\ $ Pour l'acide, on a : $n_{a}=c_{a}V_{a}$
A.N : $n_{a}=2\;10^{-2}\times 10\;10^{-3}=2\;10^{-4}$
Donc, $$\boxed{n_{a}=2\;10^{-4}\;mol}$$
$-\ $ Pour la base, on a : $n_{b}=c_{b}V_{b}$
A.N : $n_{b}=2\;10^{-2}\times 20\;10^{-3}=4\;10^{-4}$
Donc, $$\boxed{n_{b}=4\;10^{-4}\;mol}$$
2) D'après 1) nous constatons que $n_{a}<n_{b}$
Alors, à l'équilibre (après réaction) on aura : $n_{a}=0$ et $n_{b_{\text{restant}}}=n_{b}-n_{a}.$
Donc, la solution est basique.
Par conséquent, l'ajout de quelques gouttes de B.B.T dans le mélange donne une coloration bleue.
3) Calculons le volume d'acide à ajouter
A l'équivalence on a : $n_{a}=n_{b}$
Alors, $n_{a_{\text{ajout}}}+n_{a_{\text{init}}}=n_{b}$ , or $n_{b}=4\;10^{-4}\;mol$ et $n_{a_{\text{init}}}=2\;10^{-4}\;mol$
Donc, $n_{a_{\text{ajout}}}=4\;10^{-4}-2\;10^{-4}=2\;10^{-4}\;mol$
Comme $n_{a_{\text{ajout}}}=c_{a}V_{a_{\text{ajout}}}$, alors $V_{a_{\text{ajout}}}=\dfrac{n_{a_{\text{ajout}}}}{c_{a}}$
A.N : $V_{a_{\text{ajout}}}=\dfrac{2\;10^{-4}}{2\;10^{-2}}=10^{-2}$
Donc, $$\boxed{V_{a_{\text{ajout}}}=10\;ml}$$
Exercice 2
1) Écrivons l'équation bilan de la réaction
On a : $$2Al\ +\ Fe_{2}O_{3} \longrightarrow\ Al_{2}O_{3}\ +\ 2Fe$$
2) Calculons la masse de fer obtenue.
D'après l'équation bilan, on a : $\dfrac{n_{(Fe_{2}O_{3})}}{1}=\dfrac{n_{(Fe)}}{2}$
Donc, $n_{(Fe_{2}O_{3})}\times 2=n_{(Fe)}$ or, $n_{(Fe_{2}O_{3})}=\dfrac{m_{(Fe_{2}O_{3})}}{M_{(Fe_{2}O_{3})}}$
On aura alors, $2\times\dfrac{m_{(Fe_{2}O_{3})}}{M_{(Fe_{2}O_{3})}}=\dfrac{m_{(Fe)}}{M_{(Fe)}}$
Ainsi, $m_{(Fe)}=\dfrac{2\times m_{(Fe_{2}O_{3})}\times M_{(Fe)}}{M_{(Fe_{2}O_{3})}}$
avec $M_{(Fe_{2}O_{3})}=2\times 56+3\times 16=160\;g.mol^{-1}$
A.N : $m_{(Fe)}=\dfrac{2\times 3.2\;10^{3}\times 56}{160}=2240$
D'où, $$\boxed{m_{(Fe)}=2.24\;kg}$$
3) Déterminons la masse d'alumine obtenue.
D'après l'équation bilan, on a : $\dfrac{n_{(Al_{2}O_{3})}}{1}=\dfrac{n_{(Fe)}}{2}$
Alors, $n_{(Al_{2}O_{3})}\times 2=n_{(Fe)}$
Donc, $2\times\dfrac{m_{(Al_{2}O_{3})}}{M_{(Al_{2}O_{3})}}=\dfrac{m_{(Fe)}}{M_{(Fe)}}$
Ainsi, $m_{(Al_{2}O_{3})}=\dfrac{m_{(Fe)}\times M_{(Al_{2}O_{3})}}{2\times M_{(Fe)}}$
avec $M_{(Al_{2}O_{3})}=2\times 27+3\times 16=102\;g.mol^{-1}$
A.N : $m_{(Al_{2}O_{3})}=\dfrac{2240\times 102}{2\times 56}=2040$
D'où, $$\boxed{m_{(Al_{2}O_{3})}=2.04\;kg}$$
Exercice 3
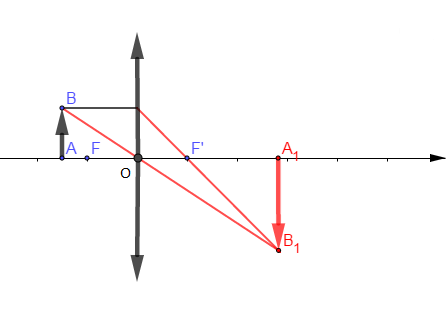
1) Construisons l'image $A_{1}B_{1}$ de l'objet $AB$

2) Caractéristiques de l'image :
$-\ $ image réelle
$-\ $ image renversée
$-\ $ image plus grande que l'objet
$-\ $ agrandissement $\gamma=\dfrac{A_{1}B_{1}}{AB}=\dfrac{1.8}{1}=1.8$
$-\ $ image sur le côté opposé $OA_{1}=2.8\;cm$, l'image se trouve donc à $2.8\;cm$ du centre optique.
3) Hypermétropie : l'œil hypermétrope n'est pas assez convergent, son cristallin a une distance focale longue. L'image se forme derrière la rétine ; elle est floue. La lentille convergente corrige cette anomalie en convergeant les rayons incidents afin que l'image se forme sur la rétine.
Exercice 4
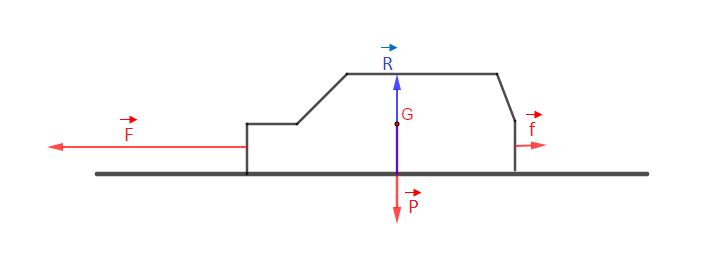
1) Représentons, par des vecteurs, les forces appliquées au mobile.

2) Calculons le travail de la force motrice.
On a $W(\vec{F})=F.d$
A.N : $W(\vec{F})=5600\times 0.8\;10^{3}=4.48$
Donc, $$\boxed{W(\vec{F})=4.48\;j}$$
Le travail du poids sur le même déplacement est nul car la force $(\vec{P})$ est perpendiculaire au déplacement.
Auteur:
Aliou ndiaye

Commentaires
Khadim diop (non vérifié)
sam, 07/31/2021 - 02:20
Permalien
Machallh
Anonyme (non vérifié)
dim, 05/14/2023 - 23:42
Permalien
Correction BFM pc 2012
Anonyme (non vérifié)
dim, 05/14/2023 - 23:42
Permalien
Correction BFM pc 2012
Ajouter un commentaire