Série d'exercices : Énergie cinétique - 1er s
Classe:
Première
Exercice 1
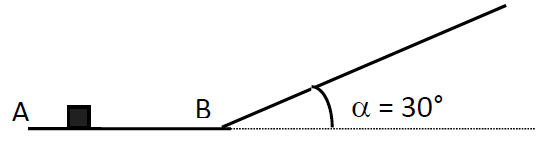
Un autoporteur de masse $m=600\,g$ est lancé depuis un point $A$ avec une vitesse initiale $V_{A}=6\,m\cdot s^{-1}$ sur un plan $AB$ horizontal de longueur $AB=3\,m$ sur lequel il glisse sans frottement, puis aborde un plan incliné $BD$, de longueur $BD=4\,m$, sur lequel les frottements seront supposés négligeables.
L'autoporteur pourra être considéré comme un solide ponctuel.
On prendra $g=10\,m\cdot s^{-2}$
1) Exprimer, puis calculer l'énergie cinétique de l'autoporteur en $A.$
2) Faire l'inventaire des forces extérieures agissant sur l'autoporteur au cours de la phase $AB.$
Définir ces forces et les représenter sur le dessin
3) a) Donner la définition d'un système pseudo-isolé ;
b) L'autoporteur est-il pseudo-isolé au cours de la phase $AB$, la phase $BD$ ?
c) En déduire la vitesse du centre d'inertie du mobile en $B$ ?
4) Soit $C_{1}$ un point du plan incliné tel que $BC_{1}=1\,m$
Calculer le travail du poids de l'autoporteur et le travail de l'action $R$ du plan sur l'autoporteur au cours du déplacement $BC_{1}.$
5) En appliquant le théorème de l'énergie cinétique au solide entre les instants $t_{B}$ et $t_{C_{1}}$ en déduire $V_{C_{1}}$
6) Soit $C_{2}$ le point de rebroussement sur le plan incliné.
En appliquant le théorème de l'énergie cinétique au solide entre les instants $t_{B}$ et $t_{C_{2}}$, en déduire $B_{C_{2}}$ la distance parcourue par le mobile avant de rebrousser chemin en $C_{2}.$
Exercice 2
Une gouttière $ABC$ sert de parcours à un mobile supposé ponctuel, de masse $m=0.1\,kg.$
Le mouvement a lieu dans un plan vertical.
On donne $g=10\,m\cdot s^{-2}.$

Donné :
$\left(\overrightarrow{OA}\;,\ \overrightarrow{OB}\right)=\pi/2\,rad$
$r=OA=OB=1\,m$
1. Sa partie curviligne $AB$ est un arc de cercle parfaitement lisse où les frottements sont négligés.
Le mobile est lancé en $A$ avec une vitesse $V_{A}=5\,m\cdot s^{-1}$ verticale dirigée vers le bas et glisse sur la portion curviligne $AB.$
1.1 Faire un bilan des forces s'appliquant sur le mobile au point $M.$
1.2 Exprimer pour chacune des forces son travail au point $M$ en fonction de $m$, $g$, $r$ et $\theta.$
1.3 Appliquer le théorème de l'énergie cinétique au point $M$ et établir l'expression littérale de la vitesse $V_{M}$ du mobile en fonction de $V_{A}$, $g$, $r$ et $\theta.$
1.4 Calculer numériquement $V_{M}$ en $B$ $($pour $\theta=0).$
2. La portion $BC$ rectiligne et horizontale est rugueuse.
Les frottements peuvent être assimilés à une force $f$ unique, constante, opposée au mouvement, d'intensité $f.$
Sachant que le mobile arrive en $C$ avec la vitesse $V_{C}=5\,m\cdot s^{-1}$, déterminer littéralement puis numériquement $f.$
On donne : $BC=1\,m$
Exercice 3
Voiture tremplin
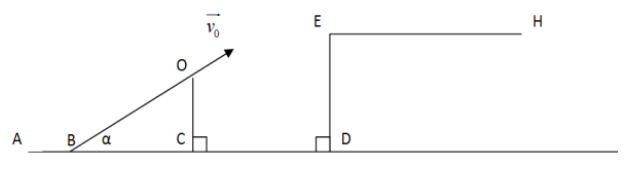
Un cascadeur veut sauter avec sa voiture sur la terrasse horizontale $EH$ d'un immeuble.
Il utilise un tremplin $BOC$ formant un angle $\alpha$ avec le sol horizontal $ABCD$ et placé à la distance $CD$ de l'immeuble.
$(OC$ et $DE$ sont des parois verticales.$)$
On prendra $g=9.81\,N\cdot kg^{-1}.$
La masse de l'automobile et du pilote est $m=1.00$ tonne.
On étudiera le mouvement de l'ensemble assimilable à un point : son centre d'inertie $G.$
Pour simplifier le problème, on considérera que, dans la phase aérienne de $O$ à $E$, les frottements sont inexistants et on admettra qu'à la date initiale le centre d'inertie $G$ quitte le point $O$ avec la vitesse $\overrightarrow{v_{0}}$ et que $G$ est confondu avec le point $E$ à l'arrivée sur la terrasse.
Données :
$\alpha=15.0^{\circ}$ ; $DE=10.0\,m$ ; $OC=8.00\,m$ ; $CD=15.0\,m.$
1) Faire le bilan des forces dans les $3$ phases $(B$ à $O$, $O$ à $E$ et $E$ à $H).$
2) Pour chacune de ces phases, dire si le système est pseudo isolé.
Justifier.
3) Déterminer le travail de chacune des forces dans chaque phase.
4) Pour une certaine valeur de $\overrightarrow{v_{0}}$, l'automobile arrive en $E$ avec une vitesse horizontale $\overrightarrow{v_{1}}$ telle que
$v_{1}=86.4\,km\cdot h^{-1}.$
Déterminer la valeur de $\overrightarrow{v_{0}}$ $($en $km\cdot h^{-1})$ en utilisant le théorème de l'énergie cinétique.
5) En considérant, qu'une fois l'automobile sur la terrasse, les frottements sont équivalents à une force constante $\overrightarrow{f}$ parallèle au déplacement et de valeur $f=500\,N$, calculer la valeur de la force de freinage $\overrightarrow{F}$ constante qui permettra au véhicule de s'arrêter sur le trajet de longueur $EH=100\,m.$
6) Le temps mis pour parcourir la distance $EH$ est $t=8.00\,s$ ; en déduire la puissance du travail de la force $\overrightarrow{F}$
Exercice 4
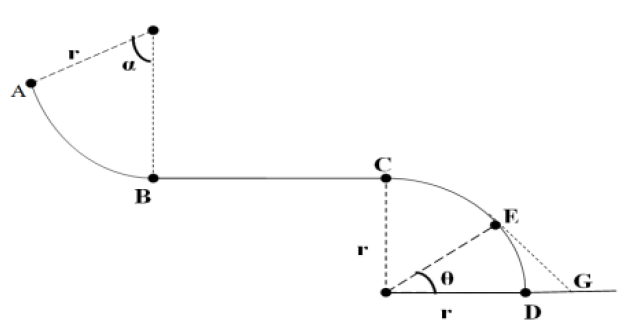
Un skieur de masse $m=80\,kg$ glisse sur un début de piste formée de trois parties $AB$, $BC$ et $CD.$
$\bullet\ $ La partie $AB$ est un arc de cercle de rayon $r=5\,m$ et de centre $O'$ tel que $AO'B=\alpha=60^{\circ}.$
$\bullet\ $ $BC$ est une partie rectiligne horizontale de longueur $r.$
$\bullet\ $ $CD$ est un quart de circonférence verticale de rayon $r$ et de centre $O.$
Toute la trajectoire est dans un même plan vertical.
Le skieur part de $A$ sans vitesse initiale.
Pour simplifier les calculs, son mouvement sera, dans tout le problème, assimilé à celui d'un point matériel.
1. Lors d'un premier essai, la piste $ABC$ est verglacée.
Les frottements sont alors suffisamment faibles pour être négligés.
Calculer, dans ces conditions, les vitesses $V_{B}$ et $V_{C}$ avec lesquelles le skieur passe en $B$ et en $C.$
2. Au cours d'un autre essai, la piste $ABC$ est recouverte de neige.
On supposera pour simplifier que la résultante des forces de frottement, constamment tangentes à la trajectoire, garde un module constant $f$ sur tout le trajet $ABC.$
2.1 Exprimer $V_{B}$ en fonction de $m$, $r$, $f$ et $g.$
2.2 Exprimer $V_{C}$ en fonction de $m$, $r$, $f$ et $V_{B}$
2.3 Calculer l'intensité de la force de frottement si le skieur arrive en $C$ avec une vitesse nulle.
3. Le skieur arrive en $C$ avec une vitesse nulle ; il aborde la partie $CD$ qui est verglacée ; les frottements seront donc négligés.
3.1 Le skieur passe en un point $E$ de la piste $CD$, défini par $(OD\ OE)=\theta$ ; $OD$ étant porté par l'horizontale.
Exprimer sa vitesse $V_{E}$ en fonction de $g$, $r$ et $\theta$
3.2 Le skieur quitte la piste en $E$ avec la vitesse $V_{E}=5.77\,m\cdot s^{-1}$, calculer la valeur de l'angle $\theta.$
4. Avec quelle vitesse le skieur atterrit-il sur la piste de réception en un point $G$
Exercice 5
Un corps de masse $500\,g$ glisse sur un trajet $ABCD.$
Il est lâché en $A$ vitesse initiale
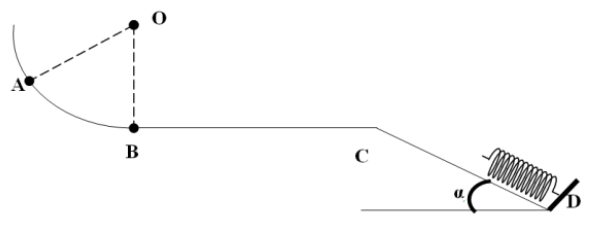
Le trajet comporte trois parties : $AB$ est un arc de cercle de rayon $r=2\,m\left(AB=\dfrac{1}{6}\text{ du cercle}\right)$, $BC$ est un trajet rectiligne horizontal de longueur $BC=5\,m$ et enfin $CD$ est un trajet rectiligne incliné d'un angle par rapport à l'horizontale.
$\sin\alpha=\dfrac{5}{100}\;,\ CD=4\,cm$
Dans tout l'exercice, on suppose que les forces de frottement n'existent qu'entre $B$ et $C.$
On prendra $g=10\,N/kg$
Un ressort est placé en $D$ comme l'indique la figure.
Sa longueur à vide est $l0=30\,cm$ et sa raideur $k=1000\,N/m$
1. Calculer la vitesse de ce corps au point $B$
2. Le corps arrive en $C$ avec une vitesse $V_{C}=\dfrac{2}{3}V_{B}.$
Calculer l'intensité de la force de frottement sur $BC$
3. Le corps arrive en $C$ et descend le plan incliné
3.1 Déterminer la vitesse avec laquelle le corps atteint le ressort.
3.2 Le corps s'accrochant au ressort, déterminer le raccourcissement maximal du ressort.
Exercice 6
Données numériques : $m=100\,g$ ; $BC=3\,m$ ;
$r=1.5\,m$ ; $f=0.32\,N$ ; $g=10\,N\cdot kg^{-1}\cdot\alpha=30^{\circ}$
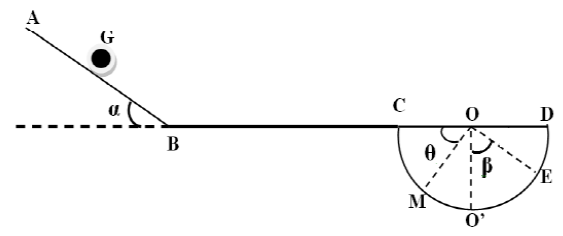
Une piste comprend un plan incliné $AB$ faisant un angle l'horizontale, une portion $BC$ rectiligne et horizontale, une portion circulaire $CD$ de centre $O$ et de rayon $r$ (figure).
Les points $A$, $B$, $C$ et $D$ sont situés dans le même plan vertical.
Les frottements sont négligés les parties $AB$ et $CD.$
Sur la portion $BC$, il existe des forces de frottements équivalentes à une $f$ unique opposée au vecteur vitesse.
On abandonne en un point $G$ du plan incliné un solide $(S)$ ponctuel de masse $m$, sans vitesse initiale.
Le solide arrive en $C$ avec une vitesse nulle.
1) Faire le bilan des forces appliquées au solide $(S)$ sur les portions $AB$ et $BC.$
2) Déterminer la longueur $GB.$
(On pourra utiliser le théorème de l'énergie cinétique).
3) Le solide $(S)$ aborde la partie circulaire $CD$ avec une vitesse nulle en $C.$
On le repère en un point $M$ par l'angle $\theta$
a) Exprimer sa vitesse $V$ au point $M$ en fonction de $g$, $r$ et puis calculer sa valeur au passage en $O'$
b) Déterminer la vitesse du solide $(S)$ au point $D.$
4) En réalité le travail des forces de frottements sur la portion $CD$ est égal à celui de la portion $BC$ et le solide $(S)$ s'immobilise au point $E$ repéré par l'angle $\beta$
a) Exprimer sa vitesse $V$ au point $M$ puis calculer sa valeur au passage en $O'.$
b) Calculer la valeur de l'angle $\beta.$
Exercice 7
1. Solide en chute verticale.
1.1 Un solide $S_{1}$, assimilé à son centre d'inertie et de masse $m_{1}=0.50\,kg$, est lâché sans vitesse, et tombe en chute libre.
Calculer la valeur $V$ de sa vitesse après une chute de hauteur : $h=80\,cm.$
1.2 En réalité la valeur de la vitesse mesurée, soit $V'$, ne vaut que $90\%$ de la valeur $V.$
1.2.1 Expliquer pourquoi.
1.2.2 Exprimer, en fonction des données, puis calculer la valeur numérique de l'action, supposée constante, de l'air sur $S_{1}$ pendant la chute de hauteur $h.$
2. Solides liés.
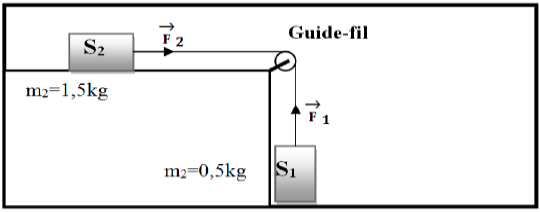
Un solide $S_{2}$, assimilé à son centre d'inertie, est posé sur un plan horizontal.
Sa masse $m_{2}$ est égale à $1.5\,kg.$
On le relie au solide $S_{1}$ par un fil inextensible et de masse négligeable.
Le solide $S_{1}$ est suspendu au bout du fil.
Le fil passe dans un guide.
Les forces de frottements du guide sur le fil sont négligées.
Le fil est juste tendu et $S_{2}$ est maintenu immobile dans la position $A_{2}$, la position de $S_{1}$ est alors $A_{1}.$
Voir Figure ci-dessus.
On lâche $S_{2}$ sans vitesse.
On considérera que le glissement de $S_{2}$ sur le plan horizontal s'effectue sans frottement.
On appelle $B_{1}$ et $B_{2}$ les positions de $S_{1}$ et de $S_{2}$, quand $S_{1}$ s'est déplacé de : $A_{1}B_{1}=h=80\,cm.$
La valeur de la vitesse $\overrightarrow{v}$ de $S_{1}$ est alors notée $v$
Au cours du déplacement des deux solides, le fil exerce une force $\overrightarrow{F_{1}}$ sur le solide $S_{1}$ et une force $\overrightarrow{F_{2}}$ sur le solide $S_{2}.$
Ces forces sont appelées tensions du fil.
On admettra que les valeurs $F_{1}$ et $F_{2}$ de ces deux forces sont constamment égales, mais cette valeur commune varie au cours du déplacement des deux solides.
2.1 Représenter sur un schéma les différentes forces s'exerçant sur le solide $S_{1}$, puis celles s'exerçant sur le solide $S_{2}$ lors de leurs mouvements.
2.2 Que vaut la distance $A_{2}B_{2}$ ?
Justifier la réponse.
2.3 On appelle $W_{2}$ le travail mécanique de la tension $\overrightarrow{F_{2}}$ du fil sur le solide $S_{2}$ lors de son déplacement $A_{2}B_{2}.$
Quel est le signe de $W_{2}$ ?
Justifier la réponse.
2.4 On appelle $W_{1}$ le travail mécanique de la tension $\overrightarrow{F_{1}}$ du fil sur le solide $S_{1}$ lors de son déplacement $A_{1}B_{1}.$
Quel est le signe de $W_{1}$ ?
Justifier la réponse.
2.5 Exprimer $W_{1}$ en fonction de $W_{2}.$
2.6 Exprimer $W_{2}$ en fonction de $m_{2}$ et $v$, puis $W_{1}$ en fonction de $m_{1}$, $v$, $g$ et $h.$
2.7 En déduire l'expression de $v$ en fonction de $m_{1}$, $m_{2}$, $g$, et $h.$
2.8 Calculer la valeur numérique de $v.$
2.9 Comparer la valeur de $v$ à celle de $V$ obtenue dans le 1.1 et proposer une explication à la forte différence observée.
2.10 Quelle est la valeur de la puissance instantanée du poids de $S_{1}$ lorsqu'il atteint $B_{1}$ ?
2.11 On recommence l'expérience précédente en faisant de sorte que les solides $S_{1}$ et $S_{2}$ se déplacent à vitesse constante de valeur $v'.$
2.11.1 Comment réaliser cette condition ?
2.11.2 Déterminer la valeur numérique des actions de contact entre le solide $S_{2}$ et le plan horizontal.
Exercice 8
Un disque de masse $m=100\,g$, de rayon $r=20\,cm$ tourne autour de l'axe perpendiculaire au disque en son centre.
1. Il est animé d'un mouvement de rotation uniforme, entretenu grâce à un moteur qui fournit une puissance de $36\,mW.$
Un point $A$, situé à la périphérie du disque est animé d'une vitesse de $2.4\,m/s.$
1.1 Calculer la vitesse angulaire du disque.
1.2 Calculer la vitesse du point $B$ situé à $2\,cm$ du centre du disque.
1.3 Calculer le moment du couple moteur.
1.4 Calculer le travail effectué par le couple moteur quand le disque tourne de $10$ tours.
2. On coupe l'alimentation du moteur : le disque s'arrête au bout de $8\,s$ après avoir tourné de $7.6$ tours.
Le frottement peut être représenté par une force constante, d'intensité $1.5\cdot10^{-2}N$, tangente au disque.
2.1 Calculer le travail de cette force pendant cette phase du mouvement.
2.2 Calculer la variation de l'énergie cinétique du disque durant cette phase
2.3 Calculer la puissance moyenne de la force de frottement durant cette phase.
2.4 Calculer la puissance (instantanée) de la force de frottement au commencement de cette phase.

Commentaires
VIANEY KOHONOU (non vérifié)
mar, 12/14/2021 - 16:51
Permalien
Pour m'informer et mieux apprendre
Téby atsé (non vérifié)
dim, 12/04/2022 - 01:12
Permalien
Apprendre la physique chimie et les maths de 1rec
Anonyme (non vérifié)
mar, 12/14/2021 - 16:52
Permalien
Merci à vous
VIANEY KOHONOU (non vérifié)
mar, 12/14/2021 - 16:54
Permalien
Pour m'informer et mieux apprendre
Anonyme (non vérifié)
mar, 12/14/2021 - 16:59
Permalien
Corrigé exo4
Kyrie Irving (non vérifié)
mar, 03/15/2022 - 02:14
Permalien
Merci à vous
aloud (non vérifié)
mer, 12/07/2022 - 11:23
Permalien
correction s'il vous plait
Anonyme (non vérifié)
mar, 12/20/2022 - 19:12
Permalien
Pdf svp
Salem (non vérifié)
jeu, 03/28/2024 - 08:46
Permalien
Merci Mr s'il vous plait pdf
Daniel (non vérifié)
sam, 11/09/2024 - 20:24
Permalien
Élève
Limule (non vérifié)
mar, 11/12/2024 - 21:28
Permalien
Être le meilleur
Pages
Ajouter un commentaire