Théorèmes de la droite des milieux - 4e
Classe:
Quatrième
I. Activité
Soit $ABC$ un triangle quelconque, $I$ milieu du segment $[AB]$ e $J$ milieu du segment $[AC].$
1) Faire une figure
2) Construire le point $K=S_{J}(I)$
3) Démontrer que $AICK$ est un parallélogramme
4) Démontrer que $BIKC$ est un parallélogramme
5) Quelle est la position des droites $(BC)\ $ et $\ (IJ)$
6) Montrer que $IJ=\dfrac{1}{2}BC$
Solution
1) et 2)
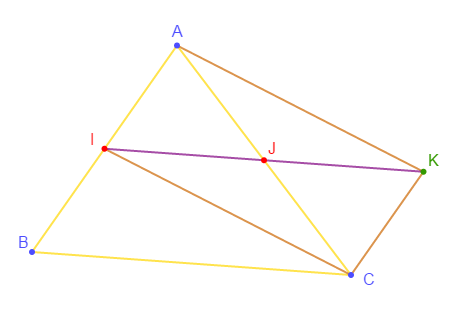

3) $J$ est milieu commun à $[AC]\ $ et $\ [IK]$ donc, $AICK$ est un parallélogramme.
4) On a : $(AB)//(KC)$ car $AICK$ est un parallélogramme.
Comme $I\in[AB]$ donc, $(BI)//(KC).$
De plus, $AI=KC$ car $AICK$ est un parallélogramme.
Comme $I$ est milieu de $[AB]$ donc, $AI=IB.$
Et finalement : $BI=KC\ $ et $\ (BI)//(KC)$ donc, $BIKC$ est un parallélogramme.
5) $BIKC$ est un parallélogramme donc, $(BC)//(IK).$
Comme $J\in[IK]$ donc, $(IJ)//(BC)$
6) $BIKC$ est un parallélogramme donc, $BC=IK.$
$J$ milieu de $[IK]$ donc, $IJ=JK\ $ et $\ IJ=\dfrac{1}{2}IK=\dfrac{1}{2}BC$
D'où, $\boxed{IJ=\dfrac{1}{2}BC}$
II. Théorème 1
Dans un triangle, la droite qui passe par les milieux des deux côtés est parallèle au troisième côté.
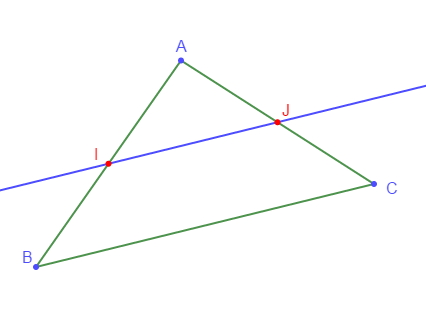
$$\left.\begin{array}{r} I\text{ milieu de }[AB]\\ \\J\text{ milieu de }[AC]\end{array}\right\rbrace\ \Rightarrow\ (IJ)//(BC)$$
Application
Soit $ABC$ un triangle, $I$ milieu de $[AB]\ $ et $\ D=S_{C}(A).$
Faire une figure et montrer que $(IC)//(BD)$
Solution
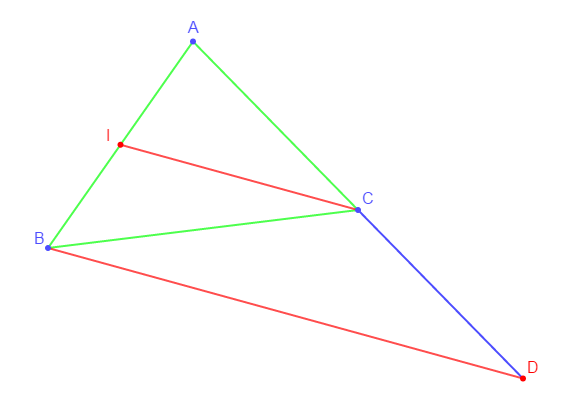
Considérons le triangle $ABD$
$I$ milieu de $[AB]$ par hypothèse
$C$ milieu $[AD]$ car $D=S_{C}(A)$
D'après Théorème 1 $(IC)//(BD).$
III. Théorème 2
Dans un triangle le segment qui joint les milieux des deux côtés quelconques a pour longueur la moitié de la longueur du troisième côté.
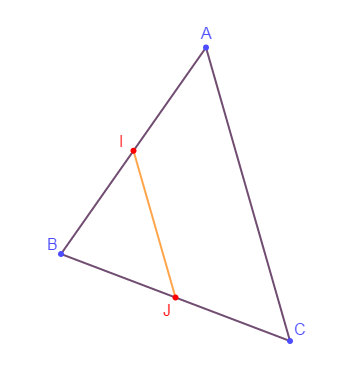
$$\left.\begin{array}{r} I\text{ milieu de }[BC]\\ \\J\text{ milieu de }[AB]\end{array}\right\rbrace\ \Rightarrow\ IJ=\dfrac{1}{2}AC$$
Application
Soit $MNL$ un triangle tel que :
$$MN=3\;cm\;,\quad ML=5\;cm\quad\text{et}\quad NL=3\;cm$$
$P=S_{N}(M)\ $ et $\ S=S_{L}(M)$
Faire une figure et calculer $PS.$
Solution

On considère le triangle $PMS$
$N$ milieu de $[PN]$ et $L$ milieu de $[MS]$
D'après le théorème 2, $NL=\dfrac{1}{2}PS$ donc,
$\begin{array}{rcl} PS&=&2NL\\ \\&=&2\times 3\;cm\\ \\&=&6\;cm\end{array}$
D'où, $\boxed{PS=6\;cm}$
IV. Théorème 3
Dans un triangle, la droite qui passe par le milieu d'un côté et qui est parallèle au deuxième côté coupe le troisième en son milieu.
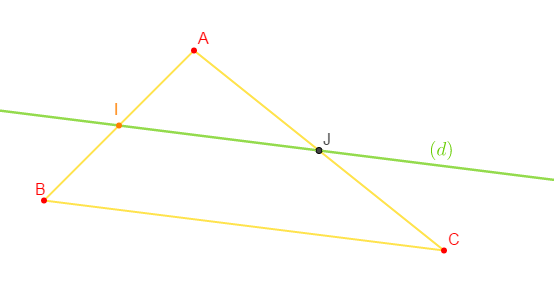
$$\left.\begin{array}{l} I\text{ milieu de }[AB]\\ \\\text{la droite }(d)\text{ qui passe par }I\\ \\\text{est parallèle à }(BC)\end{array}\right\rbrace\ \Rightarrow\ (d)\text{ coupe }[AC]\text{ en son milieu}$$
Application
Soit $KLM$ un triangle, $P$ milieu de $[KL].$
La droite passant par $P$ et parallèle à $(LM)$ coupe $[KM]$ en $S.$
Démontrer que $S$ est le milieu de $[KM].$
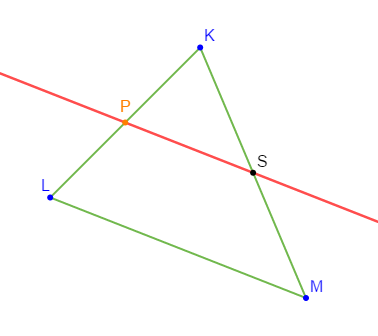
Soit $P$ milieu de $[KL]\ $ et $\ (PS)//(LM)$
D'après le théorème 3, $S$ est milieu de $[KM].$
Auteur:
Mamadou Siradji Dia

Commentaires
Mamadou TOURÉ (non vérifié)
mar, 12/21/2021 - 09:20
Permalien
Machalla.
Ndeye Khady Seck (non vérifié)
lun, 02/02/2026 - 19:38
Permalien
c'est extraordinaire
Ajouter un commentaire