Solution des exercices : Distances - 4e
Classe:
Quatrième
Exercice 1 Inégalité triangulaire
Sans faire la figure, disons dans chacun des cas ci-dessous si les points $A\;,\ B\ $ et $\ C$ sont alignés.
Pour cela, on doit vérifier si la longueur la plus grande est égale à la somme des deux autres longueurs et dans ce cas les points sont alignés.
Par contre, si cette longueur est différente alors, les points ne sont pas alignés.
$1^{er}$ cas : $AB=12\qquad AC=5\qquad BC=7$
On a : $AC+BC=5+7=12=AB$
Alors, $AB=AC+BC$
Donc, $C\in[AB]$ d'où, $A\;,\ C\;,\ B$ sont alignés dans cet ordre.
$2^{ième}$ cas : $AB=7.6\qquad AC=2.5\qquad BC=10.2$
On a : $AB+AC=7.6+2.5=10.1$
Comme $BC=10.2$ alors, $BC$ n'est pas égale à $AB+AC$
Par suite, les points $A\;,\ B\ $ et $\ C$ ne sont pas alignés.
$3^{ième}$ cas : $AB=200\qquad AC=10\qquad BC=210$
Soit : $AB+AC=200+10=210$
Alors, $BC=AB+AC$
Ce qui signifie que $A\in[BC]$ ainsi, $B\;,\ A\;,\ C$ sont alignés dans cet ordre.
$4^{ième}$ cas : $AB=0.5\qquad AC=1.06\qquad BC=0.56$
Soit : $AB+BC=0.5+0.56=1.06$
Comme $AC=1.06$ alors, on a : $AC=AB+BC$
D'où, $B\in[AC]$ et par conséquent, $A\;,\ B\;,\ C$ sont alignés dans cet ordre.
Exercice 2 Inégalité triangulaire
Dans chacun des cas ci-dessous sans faire la figure disons si le triangle $DEF$ existe.
Le triangle $DEF$ existe si, et seulement si, l'inégalité triangulaire est vérifiée pour chaque côté du triangle.
$1^{er}$ cas : $DE=5\qquad EF=2\qquad DF=2.5$
Soit : $DF+EF=2.5+2=4.5$
Comme $DE=5$ alors, on a : $DE>DF+EF$
Ainsi, l'inégalité triangulaire n'est pas vérifiée.
Par suite, le triangle $DEF$ n'existe pas.
$2^{ième}$ cas : $DE=7.5\qquad EF=5\qquad DF=4$
On a :
$DE+EF=7.5+5=12.5$ donc, $DF<DE+EF$
$DF+EF=4+5=9$ donc, $DE<DF+EF$
$DE+DF=7.5+4=11.5$ donc, $EF<DE+DF$
D'où, le triangle $DEF$ existe.
$3^{ième}$ cas : $DE=14.2\qquad EF=19\qquad DF=4.2$
Comme $DE+DF=14.2+4.2=18.4$ et que $EF=19$ alors, $EF>DE+DF$
Ainsi, l'inégalité triangulaire n'est pas vérifiée.
Par conséquent, le triangle $DEF$ n'existe pas.
$4^{ième}$ cas : $DE=105.6\qquad EF=104.6\qquad DF=102.4$
On a :
$DE+EF=105.6+104.6=210.2$ donc, $DF<DE+EF$
$DF+EF=102.4+104.6=207$ donc, $DE<DF+EF$
$DE+DF=105.6+102.4=208$ donc, $EF<DE+DF$
Alors, le triangle $DEF$ existe.
Exercice 3 Inégalité triangulaire
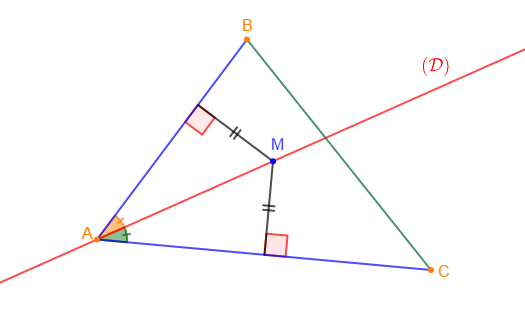
Soit $ABC$ un triangle et $M$ un point intérieur à ce triangle. La droite $(AM)$ coupe $[BC]$ en $I.$
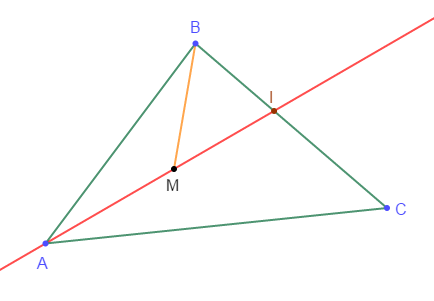
1) a) Démontrons que $IC+IB=BC\ $ et $\ IA<IC+CA.$
Comme la droite $(AM)$ coupe $[BC]$ au point $I$ alors, $I\in[BC]$
Ce qui entraine : $\boxed{IC+IB=BC}$
Par ailleurs, en appliquant l'inégalité triangulaire sur le triangle $IAC$, on obtient : $\boxed{IA<IC+CA}$
b) En déduisons que : $IA+IB<CA+CB.$
On a : $IA<IC+CA$
Donc, en ajoutant $IB$ à chaque membre de l'inégalité, on obtient : $IA+IB<IB+IC+CA$
Or, $\ IC+IB=BC$ donc, en remplaçant $IC+IB$ par $BC$, on trouve : $IA+IB<BC+CA$
Ainsi, $\boxed{IA+IB<CA+CB}$
2) Démontrons que : $MA+MB<IA+IB.$
En appliquant l'inégalité triangulaire sur le triangle $BMI$, on obtient : $MB<IM+IB$
Puis, en ajoutant $MA$ à chaque membre de l'inégalité, on obtient : $MA+MB<MA+IM+IB$
Comme $M\in[IA]$ alors, $IM+MA=IA$
Donc, en remplaçant $IM+MA$ par $IA$, on obtient : $MA+MB<IA+IB$
D'où, $\boxed{MA+MB<IA+IB}$
3) Déduisons de ce qui précède que : $MA+MB<CA+CB.$
D'après la question 2) on a : $MA+MB<IA+IB$
Or, d'après la question 1) on avait : $IA+IB<CA+CB$
Par suite, $MA+MB<IA+IB\ $ et $\ IA+IB<CA+CB$
Par conséquent, $\boxed{MA+MB<CA+CB}$
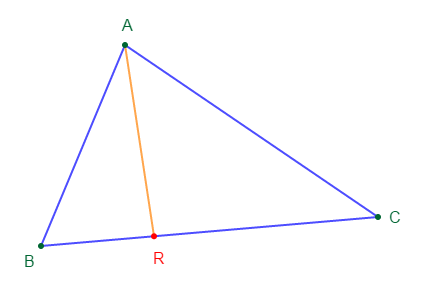
Exercice 4 Inégalité triangulaire
1) Construisons un triangle quelconque $ABC$, et choisis un point $R$ sur le segment $[BC].$

On note $p$ le périmètre du triangle $ABC.$
2) Démontrons que $AR<\dfrac{p}{2}$
$-\ $ En appliquant l'inégalité triangulaire sur le triangle $ARB$, on obtient :
$$AR<AB+BR\qquad\text{(inégalité 1)}$$
$-\ $ En appliquant l'inégalité triangulaire sur le triangle $ARC$, on obtient :
$$AR<AC+CR\qquad\text{(inégalité 2)}$$
$-\ $ En additionnant les inégalités (1) et (2) membre à membre, on trouve :
$AR+AR<AB+BR+AC+CR$
Ce qui est équivalent à :
$$2AR<AB+BR+CR+AC\qquad\text{(inégalité 3)}$$
Comme $R\in[BC]$ alors, $BR+CR=BC$
Par suite, en remplaçant $BR+CR$ par $BC$ dans l'inégalité (3), on obtient :
$$2AR<AB+BC+AC\qquad\text{(inégalité 4)}$$
Or, $\ AB+BC+AC=p$ donc, en remplaçant $AB+BC+AC$ par $p$ dans l'inégalité (4), on obtient :
$$2AR<p\ \Rightarrow\ AR<\dfrac{p}{2}$$
Ainsi, $\boxed{AR<\dfrac{p}{2}}$
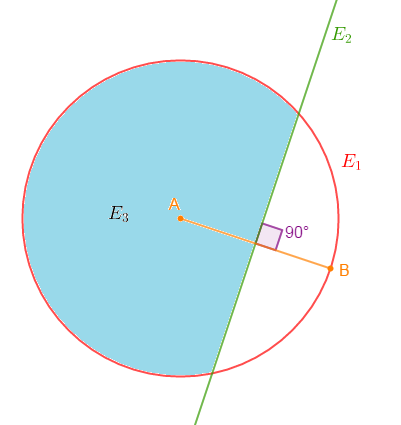
Exercice 5 Régionnement du plan
Soient $A\ $ et $\ B$ deux points distincts du plan.
1) Construisons l'ensemble $E_{1}$ des points $M$ du plan tels que : $AM=AB.$
$AM=AB$ signifie que les points $M$ sont équidistants à un point fixe $A.$ De plus, leur distance par rapport à ce point $A$ est égale à $AB.$
Cela définit alors un cercle de centre $A$ et de rayon $AB.$
D'où, l'ensemble $E_{1}$ des points $M$ du plan tels que $AM=AB$ est le cercle de centre $A$ et passant par $B.$
2) Traçons l'ensemble $E_{2}$ des points $N$ du plan tels que : $AN=BN.$
Soit : $AN=BN$ alors, $N$ est équidistant des points $A\ $ et $\ B.$
Or, tous les points appartenant à la médiatrice de $[AB]$ sont équidistants des points $A\ $ et $\ B.$
Donc, l'ensemble $E_{2}$ des points $N$ du plan tels que $AN=BN$ est la médiatrice du segment $[AB].$ C'est la droite perpendiculaire à $(AB)$ et passant par le milieu de $[AB].$
3) Colorions en bleu l'ensemble $E_{3}$ des points $M$ du plan tels que : $AM<BM\ $ et $\ AM<AB.$
En effet :
$-\ $ l'ensemble $E_{2}$ divise le plan en deux parties ; la partie contenat le point $A$ et la partie contenant le point $B.$ Donc, les points $M$ tels que $AM<BM$ sont situés dans la partie contenat le point $A.$
$-\ $ l'ensemble $E_{1}$ divise le plan en deux parties ; la partie intérieure au cercle et la partie extérieure au cercle. Ainsi, les points $M$ du plan tels que $AM<AB$ sont les points qui se sont situés à l'intérieur du cercle.
D'où, l'ensemble $E_{3}$ des points $M$ du plan tels que $AM<BM\ $ et $\ AM<AB.$ sera constitué des points situés à la fois, à gauche de la médiatrice de $[AB]$ et à l'intérieur du cercle de centre $A$ passant par $B.$

Exercice 6 Régionnement du plan
1) Marquons trois points $A\;,\ B\ $ et $\ C$ tels que :
$$AB=5\;cm\;;\ AC=8\;cm\ \text{ et }\ BC=3\;cm$$
Les trois points $A\;,\ B\ $ et $\ C$ sont alignés.
En effet, on : $AB+BC=5\;cm+3\;cm=8\;cm$
Or, $AC=8\;cm$ donc, $AC=AB+BC$
Par suite, $B\in[AC]$
Ainsi, on peut dire que les $A\;,\ B\ $ et $\ C$ sont alignés dans cet ordre.
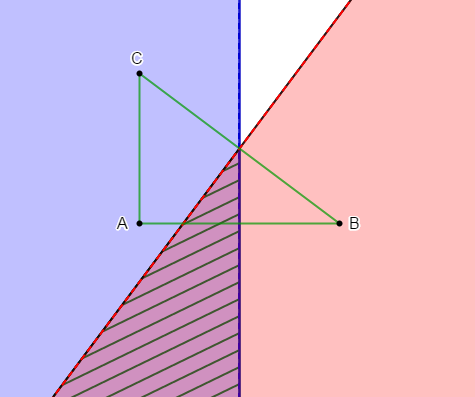
2) Colorions la partie du plan où les points sont à la fois plus prés de $C$ que de $A$ et plus éloignés de $B$ que de $C.$

Cette partie est l'ensemble des points $M$ du plan tels que : $CM<AM\ $ et $\ CM<BM$
En effet, la médiatrice du segment $[AC]$ divise le plan en deux parties ; une partie contenant le point $C$ et où les points sont plus prés de $C$ que de $A$ et une autre partie contenant le point $A.$
De même, la médiatrice du segment $[BC]$ divise le plan en deux parties ; une partie contenant le point $C$ et où les points sont plus éloignés de $B$ que de $C$ et une autre partie contenant le point $B.$
Par conséquent, la partie du plan où les points sont à la fois plus prés de $C$ que de $A$ et plus éloignés de $B$ que de $C$ est la partie contenant le point $C$ et délimitée par la médiatrice du segment $[BC].$
Exercice 7 Régionnement du plan
Soit $A\ $ et $\ B$ deux points du plan tels que : $AB=4\;cm.$
1) Traçons en bleu l'ensemble des points $M$ du plan tels que : $AM=BM.$
2) Colorions en bleu l'ensemble des points $M$ du plan tels que : $AM<BM.$
3) Plaçons un point $C$ tel que : $AC=3\;cm\ $ et $\ BC=5\;cm.$
4) Colorions en rouge l'ensemble des points $M$ du plan tels que : $BM<CM.$
5) Hachurons l'ensemble des points $M$ tels que : $AM<BM<CM.$
En effet, l'ensemble des points $M$ tels que $AM<BM<CM$ est l'ensemble des points $M$ vérifiant à la fois $AM<BM\ $ et $\ BM<CM.$
C'est donc, l'intersection des deux parties coloriées respectivement en bleu et rouge.

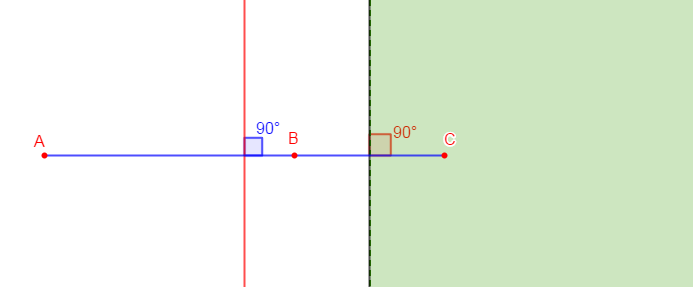
Exercice 8 Distance de deux droites parallèles
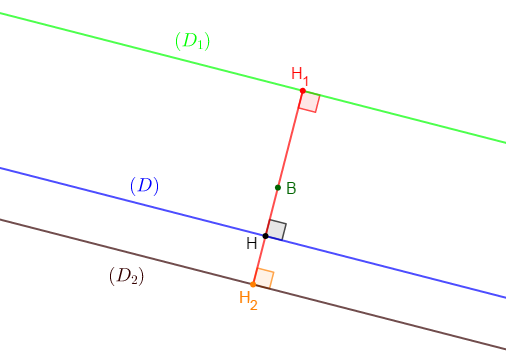
1) On donne $(D)$ et un point $B$ situé à $1\;cm$ de $(D).$
2) Construisons les droites $(D_{1})$ et $(D_{2})$ parallèle à $(D)$ et situées à $2\;cm$ du point $B.$

3) Calculons la distance des droites $(D_{1})\ $ et $\ (D_{2})$
On a :
$\begin{array}{rcl}\text{distance de } (D_{1})\ \text{ et }\ (D_{2})&=&H_{1}H_{2}\\\\&=&H_{1}B+BH_{2}\\\\&=&2\;cm+2\;cm\\\\&=&4\;cm\end{array}$
Donc, la distance des droites $(D_{1})\ $ et $\ (D_{2})$ est de $4\;cm$
En effet, les droites $(D)\;;\ (D_{1})\ $ et $\ (D_{2})$ étant parallèles alors, la perpendiculaire à ces droites passant par $B$ coupe $(D)$ en $H\;,\ (D_{1})$ en $H_{1}\ $ et $\ (D_{2})$ en $H_{2}.$
4) Calculons la distance de $(D)$ à chacune des droites $(D_{1})$ et $(D_{2})$
On a :
$\begin{array}{rcl}\text{distance de } (D)\ \text{ à }\ (D_{1})&=&HH_{1}\\\\&=&HB+BH_{1}\\\\&=&1\;cm+2\;cm\\\\&=&3\;cm\end{array}$
Ainsi, la distance de $(D)\ $ à $\ (D_{1})$ est de $3\;cm.$
On a :
$\begin{array}{rcl}\text{distance de } (D)\ \text{ à }\ (D_{2})&=&HH_{2}\\\\&=&BH_{2}-HB\\\\&=&2\;cm-1\;cm\\\\&=&1\;cm\end{array}$
Donc, la distance de $(D)$ à la droite $(D_{2})$ est égale à $1\;cm.$
Exercice 9 Positions relatives de cercles
$\mathcal{C}_{1}$ est un cercle de centre $O_{1}$ et de rayon $R_{1}\;;\ \mathcal{C}_{2}$ un cercle de centre $O_{2}$ et de rayon $R_{2}.$ Complétons le tableau ci-dessus.
$$\begin{array}{|l|c|c|c|c|c|}\hline R_{1}&9&8.2&6.4&10&5 \\ \hline R_{2}&14&7.5&4.9&23&18 \\ \hline O_{1}O_{2}&12&15.7&15.6&13&24 \\ \hline R_{1}+R_{2}& 23&15.7&11.3&33&23 \\ \hline|R_{1}-R_{2}|& |-5|=5&|0.7|=0.7&|1.5|=1.5&|-13|=13&|-13|=13 \\ \hline\text{Position relative}&\text{sécants}&\text{tangents}&\text{disjoints}&\text{tangents}&\text{disjoints} \\ \text{de }\mathcal{C}_{1}\text{ et }\mathcal{C}_{2}& &\text{extérieurement}&\text{extérieurement}&\text{intérieurement}&\text{extérieurement} \\ \hline\end{array}$$
Exercice 10 Approfondissement
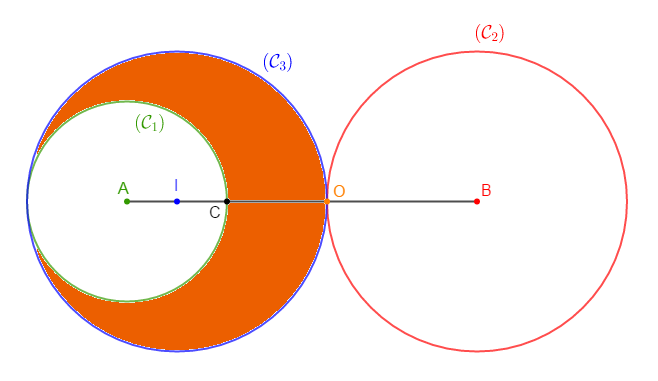
1) Sur le segment $[AB]$ de longueur $7\;cm$, plaçons les points $I\;,\ C\ $ et $\ O$ tels que : $AI=1\;cm\;;\ AC=2\;cm\ $ et $\ BO=3\;cm.$
2) a) Traçons en vert le cercle $\mathcal{C}_{1}(A\;;\ AC).$
b) Traçons en rouge le cercle $\mathcal{C}_{2}(B\;;\ BO).$
c) Traçons en bleu le cercle $\mathcal{C}_{3}(I\;;\ IO).$

3) Déterminons les positions relatives des cercles :
$\mathcal{C}_{1}$ et $\mathcal{C}_{2}\ $ ; $\ \mathcal{C}_{1}$ et $\mathcal{C}_{3}\ $ ; $\ \mathcal{C}_{2}$ et $\mathcal{C}_{3}.$
$-\ \ \mathcal{C}_{1}\ $ et $\ \mathcal{C}_{2}$ sont disjoints extérieurement.
Pour la justification, on doit vérifier que $AB>AC+BO$
En effet, on a : $AB=7\;cm\ $ et $\ AC+BO=2\;cm+3\;cm=5\;cm$
Donc, $AB>AC+BO$
D'où, les cercles $\mathcal{C}_{1}(A\;;\ AC)\ $ et $\ \mathcal{C}_{2}(B\;;\ BO)$ sont disjoints extérieurement.
$-\ \ \mathcal{C}_{1}\ $ et $\ \mathcal{C}_{3}$ sont tangents intérieurement.
Pour la justification, on doit vérifier que $AI=|AC-IO|$
En effet, on a : $AI=1\;cm$ et comme $I\in[AO]$ alors, $IO+AI=AO$
Donc, $IO=AO-AI$
Or, $O\in[AB]$ donc, $AO+BO=AB$
D'où,
$\begin{array}{rcl}AO&=&AB-BO\\\\&=&7\;cm-3\;cm\\\\&=&4\;cm\end{array}$
Ainsi, en remplaçant $AO\ $ et $\ AI$ par leur valeur, on obtient :
$\begin{array}{rcl} IO&=&AO-AI\\\\&=&4\;cm-1\;cm\\\\&=&3\;cm\end{array}$
Par suite,
$\begin{array}{rcl} |AC-IO|&=&|2\;cm-3\;cm|\\\\&=&|-1\;cm|\\\\&=&1\;cm\end{array}$
D'où, $|AC-IO|=1\;cm$
Par conséquent, $AI=|AC-IO|$
Ce qui montre que les cercles $\mathcal{C}_{1}(A\;;\ AC)\ $ et $\ \mathcal{C}_{3}(I\;;\ IO)$ sont tangents intérieurement.
$-\ \ \mathcal{C}_{2}\ $ et $\ \mathcal{C}_{3}$ sont tangents extérieurement.
Pour la justification, on doit vérifier que $IB=IO+BO$
En effet, comme $I\in[AB]$ alors, $AI+IB=AB$
D'où,
$\begin{array}{rcl} IB&=&AB-AI\\\\&=&7\;cm-1\;cm\\\\&=&6\;cm\end{array}$
Par ailleurs, $IO=3\;cm\ $ et $\ BO=3\;cm$
Donc, $IO+BO=3\;cm+3\;cm=6\;cm$
Ainsi, $IB=IO+BO$
Ce qui prouve que les cercles $\mathcal{C}_{2}(B\;;\ BO)\ $ et $\ \mathcal{C}_{3}(I\;;\ IO)$ sont tangents extérieurement.
4) Colorions l'ensemble des points $M$ du plan tel que : $AM>AC\ $ et $\ MI<IO.$
C'est la partie du plan coloriée en orange.
Ce sont les points situés à la fois à l'extérieur du cercle $\mathcal{C}_{1}$ et à l'intérieur du cercle $\mathcal{C}_{3}.$
En effet,
$-\ $ l'ensemble des points $M$ du plan tel que $AM>AC$ est représenté par tous les points du plan situés à l'extérieur du cercle $\mathcal{C}_{1}$
$-\ $ l'ensemble des points $M$ du plan tel que $MI<IO$ est représenté par tous les points du plan situés à l'intérieur du cercle $\mathcal{C}_{3}$
Ainsi, l'intersection de ces deux ensembles nous donne l'ensemble des points $M$ du plan tel que : $AM>AC\ $ et $\ MI<IO.$
Ce qui est alors représenté par la partie coloriée en orange.
Exercice 11 bissectrice
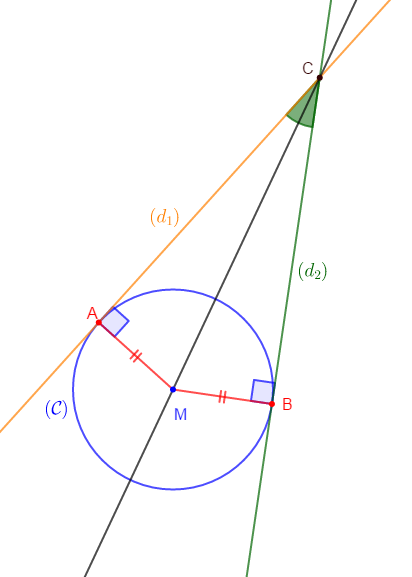
Soit un cercle $\mathcal{C}(M\;;\ 2\;cm).\ A\ $ et $\ B$ sont deux points de $(\mathcal{C})$ non diamétralement opposés. La droite $(d_{1})$ est tangente à $(\mathcal{C})$ en $A.$ La droite $(d_{2})$ est tangente à $(\mathcal{C})$ en $B.$ Les droites $(d_{1})\ $ et $\ (d_{2})$ se coupent en $C.$

Démontrons que le point $M$ appartient à la bissectrice de l'angle $ACB.$
En effet, on sait que si un point $M$ est équidistant des supports des deux côtés d'un angle alors, ce point appartient à la bissectrice de cet angle.
Donc, dans cet exercice, il suffit de montrer que $M$ est équidistant des demi-droites $[CA)\ $ et $\ [CB)$ qui sont les supports des côtés de l'angle $\widehat{ACB}.$
On a :
$(d_{1})$ est tangente à $(\mathcal{C})$ en $A$ donc, $(d_{1})$ est perpendiculaire à $[MA]$ en $A.$
D'où, la distance de $M$ à $(d_{1})$ est égale à $MA.$
Par suite, la distance de $M$ à $[CA)$ est égale à $MA.$
De la même manière, on a :
$(d_{2})$ tangente à $(\mathcal{C})$ en $B$ alors, $(d_{2})$ est perpendiculaire à $[MB]$ en $B.$
Donc, la distance de $M$ à $(d_{2})$ est égale à $MB.$
Ainsi, la distance de $M$ à $[CB)$ est égale à $MB.$
Or, on sait que $MA=MB$ car $A\ $ et $\ B$ appartiennent au cercle $(\mathcal{C}).$
Par suite,
$$\text{distance de }M\text{ à }[CA)=\text{distance de }M\text{ à }[CB)$$
Ce qui signifie que $M$ est équidistant des supports des deux côtés de l'angle $\widehat{ACB}.$
D'où, le point $M$ appartient à la bissectrice de l'angle $\widehat{ACB}.$
Exercice 12 Positions relatives de cercles
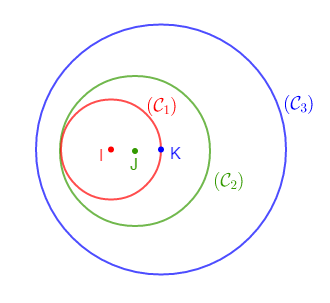
Les boucles d'oreille de la petite Sassoum sont formées de petits cercles $\mathcal{C}_{1}\;;\ \mathcal{C}_{2}$ et $\mathcal{C}_{3}$ tels que : $$\mathcal{C}_{1}(I\;;\ r_{1}=0.2)\;;\ \mathcal{C}_{2}(J\;;\ r_{2}=0.3)\ \text{ et }\ \mathcal{C}_{3}(K\;;\ r_{3}=0.5)$$
Les points $I\;,\ J\ $ et $\ K$ sont alignés dans cet ordre tels que $IJ=JK=0.1$

Déterminons la position relative des cercles :
1) $\mathcal{C}_{1}\ $ et $\ \mathcal{C}_{2}$ sont tangents intérieurement.
Pour la justification, on doit vérifier que $IJ=|r_{1}-r_{2}|$
En effet, on a : $IJ=0.1$
De plus,
$\begin{array}{rcl} |r_{1}-r_{2}|&=&|0.2-0.3|\\\\&=&|-0.1|\\\\&=&0.1\end{array}$
Donc, $|r_{1}-r_{2}|=0.1$
Ainsi, $IJ=|r_{1}-r_{2}|$
Ce qui montre que les cercles $\mathcal{C}_{1}(I\;;\ r_{1})\ $ et $\ \mathcal{C}_{2}(J\;;\ r_{2})$ sont tangents intérieurement.
2) $\mathcal{C}_{2}\ $ et $\ \mathcal{C}_{3}$ sont disjoints intérieurement.
Pour la justification, il suffit de vérifier que $JK<|r_{2}-r_{3}|$
Soit : $JK=0.1\;,\ r_{2}=0.3\ $ et $\ r_{3}=0.5$
Alors, on a :
$\begin{array}{rcl} |r_{2}-r_{3}|&=&|0.3-0.5|\\\\&=&|-0.2|\\\\&=&0.2\end{array}$
Donc, $|r_{2}-r_{3}|=0.2$
Par suite, $JK<|r_{2}-r_{3}|$
Par conséquent, les cercles $\mathcal{C}_{2}(J\;;\ r_{2})\ $ et $\ \mathcal{C}_{3}(K\;;\ r_{3})$ sont disjoints intérieurement.
3) $\mathcal{C}_{1}\ $ et $\ \mathcal{C}_{3}$ sont disjoints intérieurement.
Pour la justification, on doit vérifier que $IK<|r_{1}-r_{3}|$
En effet, comme $J\in[IK]$ alors,
$\begin{array}{rcl} IK&=&IJ+JK\\\\&=&0.1+0.1\\\\&=&0.2\end{array}$
Donc, $IK=0.2$
Aussi,
$\begin{array}{rcl} |r_{1}-r_{3}|&=&|0.1-0.5|\\\\&=&|-0.4|\\\\&=&0.4\end{array}$
Donc, $|r_{1}-r_{3}|=0.4$
Ainsi, $IK<|r_{1}-r_{3}|$
Ce qui prouve que les cercles $\mathcal{C}_{1}(I\;;\ r_{1})\ $ et $\ \mathcal{C}_{3}(K\;;\ r_{3})$ sont disjoints intérieurement.
Exercice 13 Position d'une droite et d'un cercle
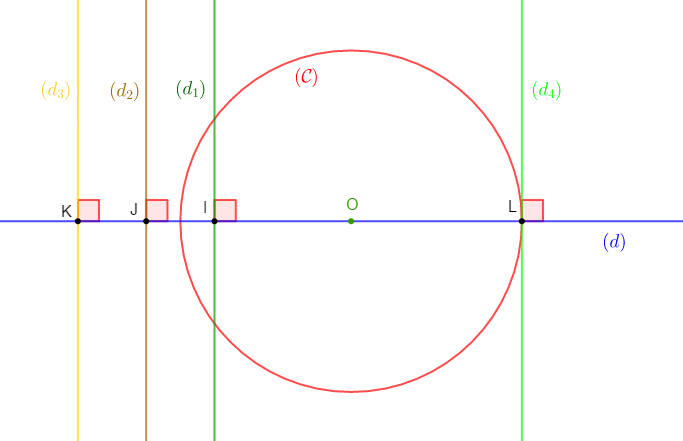
Soit $O\;;\ I\;;\ J\;;\ K\;;\ L$ des points d'une droite $(d)$ tels que :
$OI=4\;cm\;;\quad OJ=6\;cm\;;\quad OK=8\;cm\;;\quad OL=5\;cm$
$O\in[IL]\;;\quad O\notin[IJ]\;;\quad O\notin[IK].$
1) Construisons le cercle $\mathcal{C}$ de centre $O$ et de $5\;cm$ de rayon.
2) Traçons les perpendiculaires $(d_{1})\;;\ (d_{2})\;;\ (d_{3})\ $ et $\ (d_{4})$ à la droite $(d)$ respectivement en $I\;;\ J\;;\ K\ $ et $\ L.$

3) Déterminons la position relative de chacune de ces droites par rapport au cercle $(\mathcal{C})$
$-\ \ (d_{1})\ $ et $\ (\mathcal{C})$ sont sécants.
En effet, soit $OI$ la distance du point $O$ à la droite $(d_{1}).$
Comme $OI$ est inférieure au rayon du cercle $(\mathcal{C})$ de centre $O$ alors, $(d_{1})\ $ et $\ (\mathcal{C})$ sont sécants.
$-\ \ (d_{2})\ $ et $\ (\mathcal{C})$ sont disjoints.
Soit $OJ$ la distance du point $O$ à la droite $(d_{2}).$
Or, $OJ$ est supérieure au rayon du cercle $(\mathcal{C})$ de centre $O.$
Par conséquent, la droite $(d_{2})\ $ et $\ (\mathcal{C})$ sont disjoints.
$-\ \ (d_{3})\ $ et $\ (\mathcal{C})$ sont disjoints
Soit $OK$ la distance du point $O$ à la droite $(d_{3}).$
Comme $OK$ est supérieure au rayon du cercle $(\mathcal{C})$ de centre $O$ alors, $(d_{3})\ $ et $\ (\mathcal{C})$ sont disjoints.
$-\ \ (d_{4})\ $ et $\ (\mathcal{C})$ sont tangents en $L.$
$OL$ est la distance du point $O$ à la droite $(d_{4}).$
Or, $OL$ est égale au rayon du cercle $(\mathcal{C})$ de centre $O.$
Donc, la droite $(d_{4})\ $ et $\ (\mathcal{C})$ sont tangents en $L.$
Exercice 14 bissectrice et médiatrice
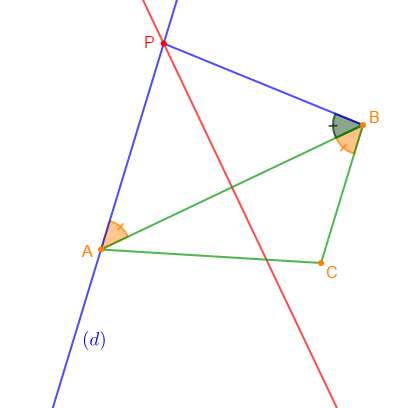
$ABC$ est un triangle. La droite $(d)$ est la parallèle à $(BC)$ qui passe par $A.$ La médiatrice de $[AB]$ coupe la droite $(d)$ en $P.$

1) Démontrons que les angles $\widehat{PAB}\ $ et $\ \widehat{CBA}$ ont des mesures égales.
En effet, $(d)\ $ et $\ (BC)$ sont deux droites parallèles coupées par la même sécante $(AB).$
Or, on sait que deux droites parallèles coupées par une sécante déterminent deux angles alternes internes de même mesure.
Donc, $\widehat{PAB}\ $ et $\ \widehat{CBA}$ sont deux angles alternes internes de même mesure.
D'où,
$$mes\;(\widehat{PAB})=mes\;(\widehat{CBA})$$
2) Démontrons que $PAB$ est isocèle en $P.$
On a : $P$ appartient à la médiatrice de $[AB].$
Or, on sait que tout point appartenant à la médiatrice d'un segment est équidistant des extrémités de ce segment.
Donc, le point $P$ est équidistant des points $A\ $ et $\ B.$
Ce qui signifie alors : $PA=PB$
Par conséquent, le triangle $PAB$ est isocèle en $P$ car, ses deux côtés $[PA]\ $ et $\ [PB]$ ont la même longueur.
3) Démontrons que la droite $(AB)$ est bissectrice de l'angle $\widehat{PBC}.$
Comme le triangle $PAB$ est isocèle en $P$ alors, les angles $\widehat{PAB}\ $ et $\ \widehat{PBA}$ ont des mesures égales.
Ce qui signifie : $$mes\;(\widehat{PAB})=mes\;(\widehat{PBA})\qquad\text{égalité 1}$$
Par ailleurs, on avait montré à la question 1) que $mes\;(\widehat{PAB})=mes\;(\widehat{CBA})$
Donc, en remplaçant $mes\;(\widehat{PAB})$ par $mes\;(\widehat{CBA})$ dans l'égalité $1$, on obtient :
$$mes\;(\widehat{CBA})=mes\;(\widehat{PBA})\qquad\text{égalité 2}$$
Par suite, $\widehat{PAB}\ $ et $\ \widehat{CBA}$ sont deux angles adjacents de même mesure et qui ont en commun le côté $(AB)$
Ainsi, la droite $(AB)$ passe par le sommet $B$ de l'angle $\widehat{PBC}$ et partage cet angle en deux angles de même mesure.
Par conséquent, la droite $(AB)$ est bissectrice de l'angle $\widehat{PBC}.$

Exercice 17
Pour chacun des énoncés ci-dessous, trois réponses $a\;,\ b\ $ et $\ c$ sont données dont une seule est juste.
Écrivons le numéro de l'énoncé et la réponse choisie.
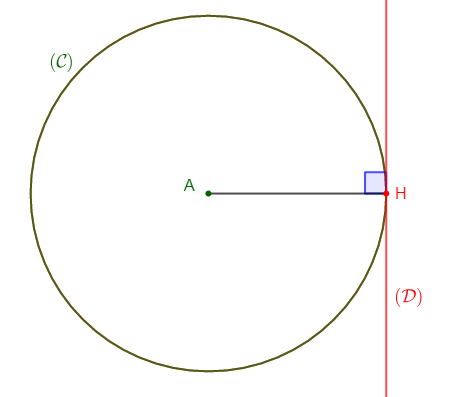
1) $(\mathcal{C})$ est un cercle de centre $O$ et de rayon $4\;cm\ $ et $\ (\mathcal{D})$ une droite à une distance de $6\;cm$ du point $O.$

b) $(\mathcal{D})\ $ et $\ (\mathcal{C})$ sont disjoints.
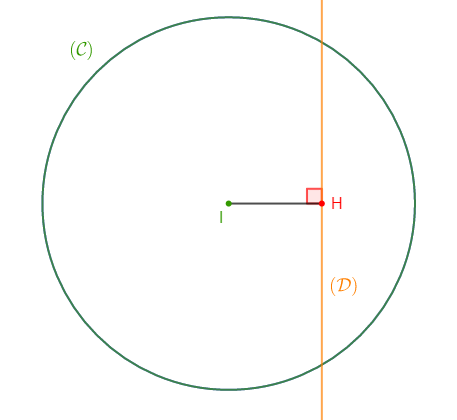
2) $(\mathcal{C})$ est un cercle de centre $A$ et de rayon $6\;cm\ $ et $\ (\mathcal{D})$ une droite à une distance de $6\;cm$ du point $A.$

c) $(\mathcal{D})\ $ et $\ (\mathcal{C})$ sont tangents.
3) $(\mathcal{C})$ est un cercle de centre $I$ et de rayon $6\;cm\ $ et $\ (\mathcal{D})$ une droite à une distance de $3\;cm$ du point $I.$

a) $(\mathcal{D})\ $ et $\ (\mathcal{C})$ sont sécants.
Exercice 18
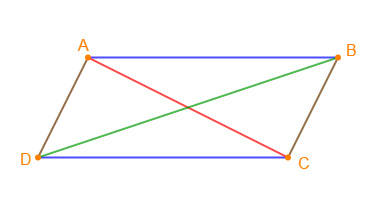
Soit $ABCD$ un parallélogramme.
Démontrons que :
$$AC<AB+BC\quad\text{ et }\quad BD<AB+BC$$
Considérons le triangle $ABC.$
En appliquant l'inégalité triangulaire sur ce triangle $ABC$, on obtient :
$$AC<AB+BC\qquad(\text{inégalité 1})$$
Par ailleurs, en appliquant l'inégalité triangulaire sur le triangle $BCD$, on obtient :
$$BD<DC+BC\qquad(\text{inégalité 2})$$
Mais comme $ABCD$ est un parallélogramme alors, on a :
$$DC=AB$$
Ainsi, en remplaçant $DC$ par $AB$ dans l'inégalité $2$, on obtient :
$$BD<AB+BC\qquad(\text{inégalité 3})$$

Autre méthode :
On peut aussi appliquer l'inégalité triangulaire sur le triangle $ABD.$
Ce qui donne :
$$BD<AB+AD$$
Or, $AD=BC$ car $ABCD$ est un parallélogramme. Donc, en remplaçant $AD$ par $BC$, on obtient :
$$BD<AB+BC$$
Exercice 19
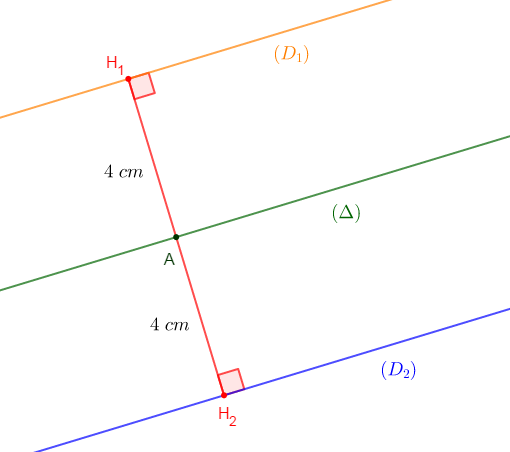
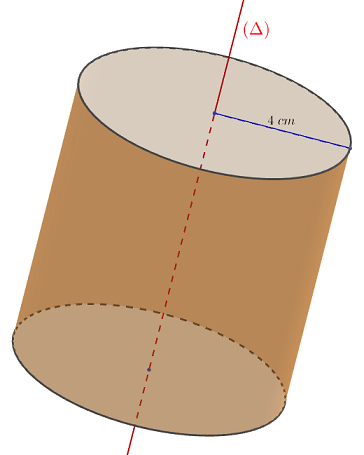
Traçons une droite $(\Delta).$
$-\ $ Dans le plan : l'ensemble des points situés à $4\;cm$ de la droite $(\Delta)$ est représenté par les droites $(D_{1})\ $ et $\ (D_{2}).$

$-\ $ Dans l'espace : l'ensemble des points situés à $4\;cm$ de cette droite est représenté par la surface latérale du cylindre d'axe $(\Delta)$ et de rayon de base $4\;cm.$

En effet, les points situés à $4\;cm$ de $(\Delta)$ sont les points situés sur des droites parallèles à $(\Delta)$ et à une distance de $4\;cm.$
Donc, l'ensemble des points situés à $4\;cm$ de $(\Delta)$ sera représenté par une infinité de droites situées à $4\;cm$ autour de cette droite $(\Delta).$
Ce qui forme alors, la surface latérale du cylindre d'axe $(\Delta)$ et de rayon de base $4\;cm.$
Exercice 20
1) On appelle bissectrice d'un angle toute droite passant par le sommet de celui-ci et qui le partage en deux angles de même mesure.
2) $ABC$ est un triangle, construisons l'ensemble des points $M$ situés à égale distance des demi-droites $[AC)\ $ et $\ [AB).$

En effet, on sait que, si un point $M$ appartient à la bissectrice d'un angle alors, il est équidistant des supports des deux côtés de l'angle.
Par conséquent, l'ensemble des points $M$ situés à égale distance des demi-droites $[AC)\ $ et $\ [AB)$ est représenté par la bissectrice de l'angle $\widehat{A}$ dont les supports des deux côtés sont $[AC)\ $ et $\ [AB).$
On note cet ensemble : la droite $(\mathcal{D})$
Exercice 21
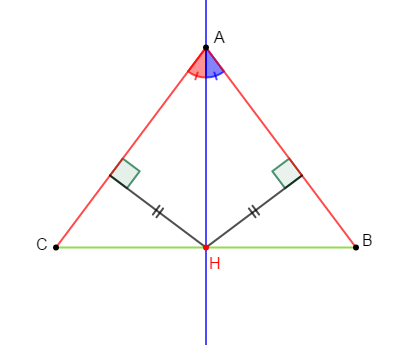
$ABC$ est un triangle isocèle en $A.$
$H$ est le pied de la médiane issue de $A.$

Démontrons que le point $H$ est équidistant des côtés $[AB]\ $ et $\ [AC].$
Comme $ABC$ est un triangle isocèle en $A$ alors, la médiane $(AH)$ issue de $A$ est aussi bissectrice de l'angle $\widehat{A}.$
Ainsi, $H$ appartient à la bissectrice de l'angle $\widehat{A}$ dont les côtés sont $[AB]\ $ et $\ [AC].$
Or, on sait que dans un triangle, si un point appartient à la bissectrice d'un angle alors, il est équidistant des deux côtés de l'angle.
Par conséquent, le point $H$ est équidistant des côtés $[AB]\ $ et $\ [AC]$ de l'angle $\widehat{A}.$
Exercice 22
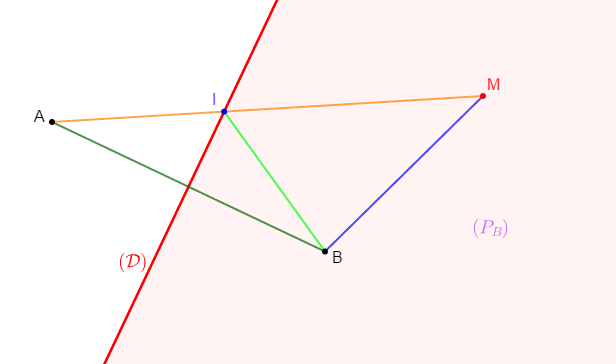
1) Traçons un segment $[AB]$, puis traçons sa médiatrice $(\mathcal{D}).$
2) Marquons un point $M$ dans le demi-plan $(P_{B})$, de frontière $(\mathcal{D})$, contenant le point $B$, puis traçons le segment $[MA]$ qui coupe $(\mathcal{D})$ en $I.$

3) En considérant le triangle $MIB$, montrons que $MI+IB>MB.$
En appliquant l'inégalité triangulaire sur le triangle $MIB$, on obtient : $MB<MI+IB$
Ce qui peut encore s'écrire :
$$MI+IB>MB$$
4) Montrons que $IB=IA$ et déduisons-en que $MA>MB.$
Comme $(\mathcal{D})$ est médiatrice de $[AB]$ alors, pour tout point $M$ appartenant à la droite $(\mathcal{D})$, on a :
$$MA=MB$$
Or, le point $I$ appartient à $(\mathcal{D}).$
Donc, $I$ vérifie : $IA=IB$
D'où, on a :
$$IB=IA$$
Par ailleurs, d'après la question 3), on a : $MI+IB>MB$
Or, nous venons juste de montrer que $IB=IA.$
Donc, en remplaçant $IB$ par $IA$, on obtient :
$$MI+IA>MB$$
De plus, on constate que $I\in[AM].$ Donc, $MI+IA=MA$
Par suite, en remplaçant $MI+IA$ par $MA$, on obtient :
$$MA>MB$$
Exercice 23
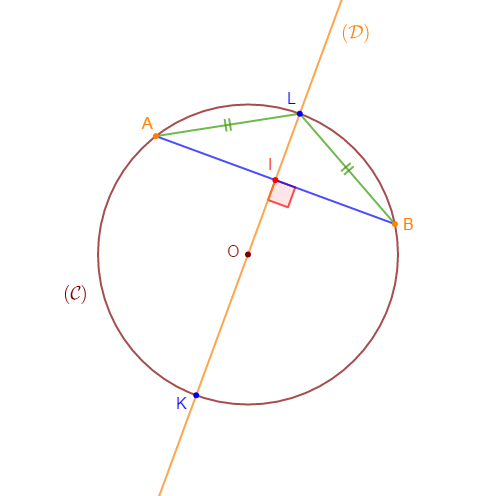
1) Traçons un cercle $(\mathcal{C})$ de centre $O$ et de rayon $3\;cm.$
2) Marquons deux points $A\ $ et $\ B$ sur le cercle non diamétralement opposés.
3) Traçons la droite $(\mathcal{D})$ perpendiculaire à $(AB)$ et passant par $O.$
Elle coupe $(\mathcal{C})$ en $L\ $ et $\ K$

4) a) Montrons que $(\mathcal{D})$ est la médiatrice de $[AB].$
En effet, on sait que la médiatrice d'un segment est la droite passant par le milieu de celui-ci et qui lui est perpendiculaire.
Or, on a : $(\mathcal{D})$ perpendiculaire à $(AB)$ au point $I.$
De plus, $[LK]$ est un diamètre de $(\mathcal{C}).$ Donc, c'est un axe de symétrie de ce cercle.
Ainsi, les points $A\ $ et $\ B$ sont symétriques par rapport à $(\mathcal{D}).$
Par suite, $AI=IB$ et alors, $I$ est milieu de $[AB].$
Donc, $(\mathcal{D})$ passe par le milieu $I$ de $[AB]$ et $(\mathcal{D})$ est perpendiculaire à $(AB).$
Par conséquent, $(\mathcal{D})$ est la médiatrice de $[AB].$
4) b) Déduisons-en que $LA=LB.$
On a : $(\mathcal{D})$ médiatrice de $[AB]\ $ et $\ L\in(\mathcal{D}).$
Or, on sait que tout point de la médiatrice d'un segment est équidistant des extrémités de ce segment.
Donc, le point $L$ appartenant à $(\mathcal{D})$ ; médiatrice de $[AB]$, est équidistant des points $A\ $ et $\ B.$
D'où, $$LA=LB$$
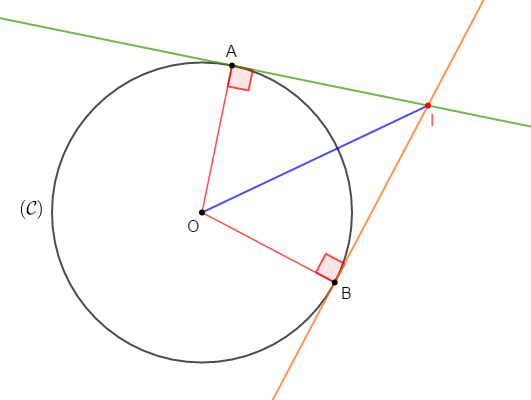
Exercice 24
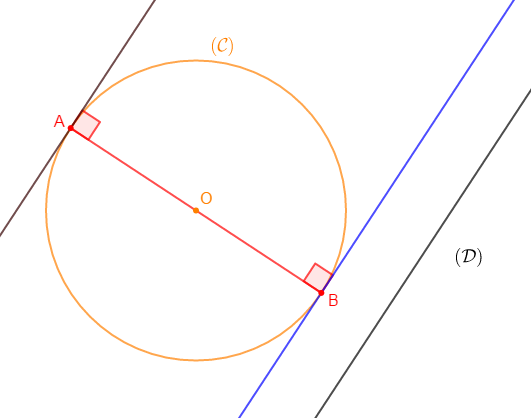
1) Construisons un cercle $\mathcal{C}(O\;;\ 3\;cm)$ et une droite $(\mathcal{D})$ disjoints.
2) Traçons les droites tangentes à $(\mathcal{C})$ et parallèles à $(\mathcal{D}).$

Exercice 25
1) Construisons un cercle $\mathcal{C}(O\;;\ 3\;cm)$ et marquons un point $I$ tel que $OI=5\;cm.$
2) Construisons les tangentes à $(\mathcal{C})$ passant par $I.$

Exercice 26
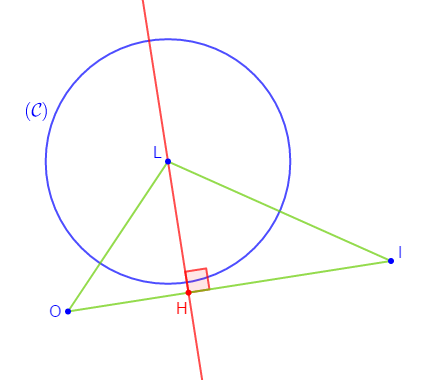
$LOI$ est un triangle, $H$ le pied de la hauteur issue de $L.$
$(\mathcal{C})$ est le cercle de centre $L$ et de rayon strictement inférieur à $LH.$

Démontrons que le cercle $(\mathcal{C})$ et la droite $(OI)$ sont disjoints.
Comme $L$ est le centre du cercle $(\mathcal{C})\ $ et $\ H$ le pied de la hauteur issue de $L$ alors, la distance du centre $L$ du cercle $(\mathcal{C})$ à la droite $(OI)$ est égale à $LH.$
Or, le rayon du cercle $(\mathcal{C})$ de centre $L$ est strictement inférieur à $LH.$
Ce qui signifie que la distance du centre $L$ du cercle $(\mathcal{C})$ à la droite $(OI)$ est strictement supérieure au rayon de $(\mathcal{C}).$
Par conséquent, le cercle $(\mathcal{C})$ et la droite $(OI)$ sont disjoints.
Exercice 27
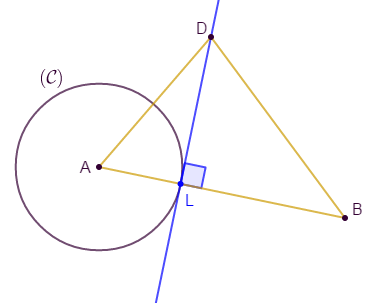
$ABD$ est un triangle, $L$ le pied de la hauteur issue de $D.$
$(\mathcal{C})$ est le cercle de centre $A$ et de rayon $AL.$

Démontrons que $(\mathcal{C})\ $ et $\ (DL)$ sont tangents.
Comme $L$ est le pied de la hauteur issue de $D$ alors, les droites $(DL)\ $ et $\ (AB)$ sont perpendiculaires en $L.$
Ainsi, la distance du point $A$ à la droite $(DL)$ est égale à $AL.$
Par suite, le rayon $AL$ du cercle reste égal à la distance du centre $A$ de ce cercle à la droite $(DL).$
D'où, $(\mathcal{C})\ $ et $\ (DL)$ sont tangents.
Exercice 28
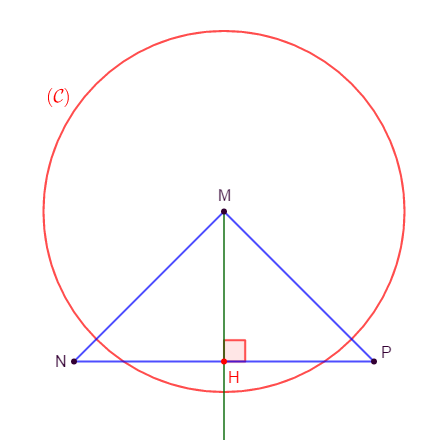
$MNP$ est un triangle isocèle en $M\;,\ H$ le milieu de $[NP].$

Démontrons que le cercle $(\mathcal{C})$ de centre $M$ et de rayon strictement supérieur à $MH\ $ et $\ (NP)$ sont sécants.
Comme $MNP$ est isocèle en $M\ $ et $\ H$ le milieu de $[NP]$ alors, la médiane $(MH)$ issue de $M$ est aussi médiatrice du segment $[NP].$
Ainsi, $H$ est le pied de la perpendiculaire issue de $M.$
Par suite, $MH$ est la distance du point $M$ à la droite $(NP).$
Or, le rayon du cercle de centre $M$ est strictement supérieur à $MH.$
Donc, la distance du centre $M$ de ce cercle à la droite $(NP)$ est strictement inférieure au rayon de ce cercle.
Par conséquent, le cercle $(\mathcal{C})$ de centre $M$ et de rayon strictement supérieur à $MH$ et la droite $(NP)$ sont sécants.
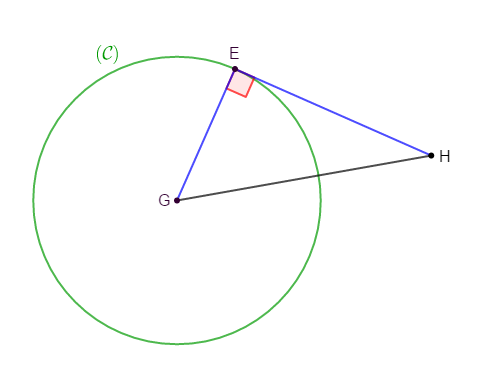
Exercice 29
$EGH$ est un triangle rectangle en $E.$
$(\mathcal{C})$ est le cercle de centre $G$ et de rayon $EG.$

Démontrons que $(\mathcal{C})\ $ et $\ (EH)$ sont tangents.
Comme $EGH$ est un triangle rectangle en $E$ alors, les droites $(EG)\ $ et $\ (EH)$ sont perpendiculaires en $H.$
Par suite, le point $E$ est le pied de la perpendiculaire passant par $G.$
Ainsi, $EG$ est la distance de $G$ à la droite $(EH).$
Par ailleurs, on sait que $(\mathcal{C})$ est le cercle de centre $G$ et de rayon $EG.$
Donc, le rayon du cercle $(\mathcal{C})$ est égal à la distance du centre $G$ de ce cercle à la droite $(EH).$
D'où, $(\mathcal{C})\ $ et $\ (EH)$ sont tangents.
Auteur:
Diny Faye

Commentaires
Anonyme (non vérifié)
dim, 03/21/2021 - 18:23
Permalien
Je voulais voir la correction
Aguibou (non vérifié)
jeu, 04/29/2021 - 19:08
Permalien
Je veux la correction des
Mouhamadou sama... (non vérifié)
mar, 12/28/2021 - 23:42
Permalien
Demande d'exercice 18/19/20/21/22/23
Ajouter un commentaire