Solution des exercices : Barycentre - 2nd

Classe: 
Seconde
 

Exercice 1

A  et  B sont deux points distincts.
 
1) Justifions qu'il existe un point G barycentre de (A, 2)  et  (B, 3).
 
Comme la somme des coefficients de pondération (2+3=5) est différente de zéro (0) et que A  et  B sont distincts alors, il existe un point G barycentre de (A, 2)  et  (B, 3).
 
2) Exprimons →AG en fonction de →AB.
 
G barycentre de (A, 2)  et  (B, 3) donc, G vérifie : 2→GA+3→GB=→0
Ainsi,
 
2→GA+3→GB=→0⇔2→GA+3(→GA+→AB)=→0⇔2→GA+3→GA+3→AB=→0⇔5→GA+3→AB=→0⇔5→GA=−3→AB⇔5→AG=3→AB⇔→AG=35→AB
 
D'où, →AG=35→AB
 
Plaçons G.
 

 

Exercice 2

Soit A  et  B deux points distincts.
 
1) Justifions qu'il existe un point G barycentre de (A, 0)  et  (B, −3).
 
En effet, A  et  B sont deux points distincts.
 
En calculant la somme de leur coefficient de pondération, on trouve :
−3+0=−3≠0
On constate alors que la somme des coefficients de pondération est non nulle ; c'est-à-dire, est différente de zéro.
 
Par conséquent, il existe un point G barycentre de (A, 0)  et  (B, −3). 
 
2) Exprimons →AG en fonction de →AB.
 
G étant barycentre de (A, 0)  et  (B, −3) alors, d'après la propriété caractéristique, on a : pour tout point M du plan,
 
→MG=0×→MA−3×→MB0−3=−3−3→MB=→MB
 
D'où,
→MG=→MB
Ainsi, en remplaçant M par A, on obtient : →AG=→AB
 
Plaçons G.
 
Comme →AG=→AB alors, G  et  B sont confondus.

 

 

Exercice 3

G est le barycentre de (A; 13)  et  (B; −56). G′ est le barycentre de (A, 2)  et  (B, −5).
 
Comparons G  et  G′.
 
Soit G est le barycentre de (A; 13)  et  (B; −56) alors, 13→GA−56→GB=→0
 
Or, d'après la propriété d'homogénéité, le barycentre reste inchangé si on multiplie ses coefficients par un même réel non nul.
 
Donc, en multipliant par 6, on obtient :
 
6×(13→GA−56→GB)=6×→0⇔63→GA−6×56→GB=→0⇔2→GA−5→GB=→0
 
Par suite, G est aussi le barycentre de (A, 2)  et  (B, −5).
 
Or, par hypothèse, G′ est le barycentre de (A, 2)  et  (B, −5).
 
Par conséquent, G=G′

Exercice 4

Sur une droite, on donne trois points A, B  et  G tels que →GA=−25→GB
 
Trouvons des réels a  et  b tels que G soit le barycentre du système {(A, a); (B; b)}
 
En effet, G doit vérifier :
a→GA+b→GB=→0
On a :
 
→GA=−25→GB⇔5→GA=−2→GB⇔5→GA+2→GB=→0
 
Par suite, la relation 5→GA+2→GB=→0 prouve que G est barycentre du système {(A, 5); (B; 2)}
 
D'où, a=5  et  b=2

Exercice 5

Soient A  et  B deux points distincts et G le barycentre de (A, 3)  et  (B, 2).
 
1) La méthode du parallélogramme
 
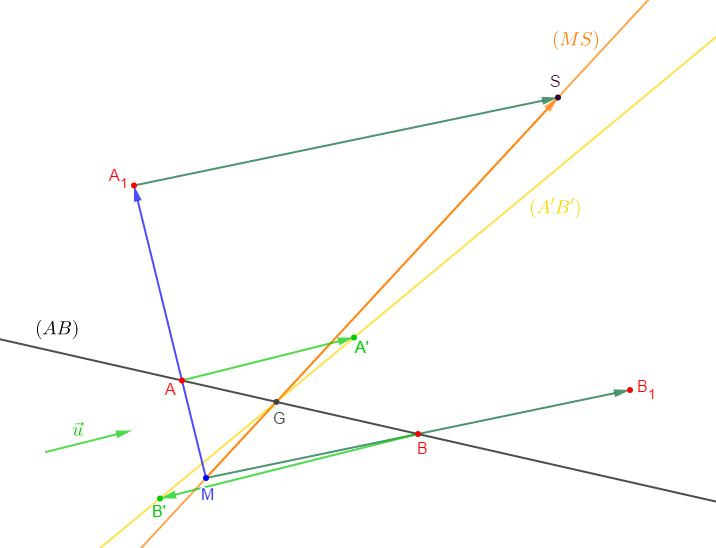
Soit M un point n'appartenant pas à (AB). Construisons les points A1, B1  et  S tels que :
→MA1=3→MA;→MB1=2→MBet→MS=→MA1+→MB1
Montrons alors que les droites (MS)  et  (AB) sont sécantes en G.
 
On a : G le barycentre de (A, 3)  et  (B, 2) alors,
3→GA+2→GB=→0 ⇒ 3→GA=−2→GB
Donc, A, B  et  G sont alignés. D'où, G∈(AB)
 
Par ailleurs, →MS=→MA1+→MB1
 
Or, →MA1=3→MA  et  →MB1=2→MB
 
Donc, en remplaçant, on obtient : →MS=3→MA+2→MB
 
Comme G est barycentre de (A, 3)  et  (B, 2) alors,
∀M∈P;  3→MA+2→MB=5→MG
Par suite,
→MS=5→MG
Ainsi, les points M, S  et  G sont alignés. D'où, G∈(MS)
 
G∈(AB)  et  G∈(MS) donc, G∈(AB)∩(MS)
 
Ce qui prouve que les droites (MS)  et  (AB) sont sécantes en G.
 
2) La méthode des parallèles
 
Soit →u un vecteur non colinéaire à →MA. Construisons les points A′  et  B′ tels que :
→AA′=2→u  et  →BB′=−3→u
Montrons que les droites (A′B′)  et  (AB) sont sécantes en G.
 
En multipliant le vecteur →AA′ par 3 et le vecteur →BB′ par 2, on obtient :
3→AA′=6→uet2→BB′=−6→u
Ainsi, 3→AA′+2→BB′=6→u−6→u=→0
 
Par suite,
 
3→AA′+2→BB′=→0⇒3(→AG+→GA′)+2(→BG+→GB′)=→0⇒3→AG+3→GA′+2→BG+2→GB′=→0⇒3→AG+2→BG⏟=→0+3→GA′+2→GB′=→0⇒3→GA′+2→GB′=→0
 
Donc, G est aussi barycentre de de (A′, 3)  et  (B′, 2)
 
Ainsi, les points A′, B′  et  G sont alignés. D'où, G∈(A′B′)
 
G∈(AB)  et  G∈(A′B′) alors, G∈(AB)∩(A′B′)
 
Cela montre que les droites (A′B′)  et  (AB) sont sécantes en G.
 
 

Exercice 6

Soient A  et  B deux points distincts.
 
Dans chacun des cas suivants, déterminons deux réels α  et  β tel que G soit le barycentre du système (A; α), (B; β)
 
Pour cela, G doit vérifier la relation
α→GA+β→GB=→0ouα→AG+β→BG=→0
a) Soit :
 
→AG=2→GB⇒→AG−2→GB=→0⇒→AG+2→BG=→0
 
Donc, G est le barycentre du système (A; 1), (B; 2)
 
b) On a :
 
→AB+→GB=3→GA⇒→AG+→GB+→GB−3→GA=→0⇒−→GA+2→GB−3→GA=→0⇒−4→GA+2→GB=→0
 
D'où, G est le barycentre du système (A; −4), (B; 2)
 
c) On a :
 
3→AB+→GA=→0⇒3(→AG+→GB)+→GA=→0⇒3→AG+3→GB+→GA=→0⇒−3→GA+3→GB+→GA=→0⇒−2→GA+3→GB=→0
 
Ainsi, G est le barycentre du système (A; −2), (B; 3)

Exercice 7

Dans chacun des cas suivants, trouvons des réels α  et  β tels que A soit barycentre de {(B; α) (C; β)}
 
De la même manière que dans l'exercice précédent, A doit vérifier la relation
α→AB+β→AC=→0ouα→BA+β→CA=→0
1) On a : →AB−2→CA=→0 ⇒ →AB+2→AC=→0
 
Donc, A est barycentre de {(B; 1) (C; 2)}
 
2) Soit :
 
→BA=3→AC⇒→BA−3→AC=→0⇒→BA+3→CA=→0
 
A est donc barycentre de {(B; 1) (C; 3)}
 
3) On a :
 
2→BC+→AC=→0⇒2(→BA+→AC)+→AC=→0⇒2→BA+2→AC+→AC=→0⇒2→BA+3→AC=→0⇒−2→AB+3→AC=→0
 
D'où, A est barycentre de {(B; −2) (C; 3)}
 
4) Soit :
 
→AB+→AC+→BC=2→BA⇒→AB+→AC+→BA+→AC−2→BA=→0⇒→AB+→AC−→AB+→AC+2→AB=→0⇒2→AB+2→AC=→0
 
D'où, A est barycentre de {(B; 2) (C; 2)}

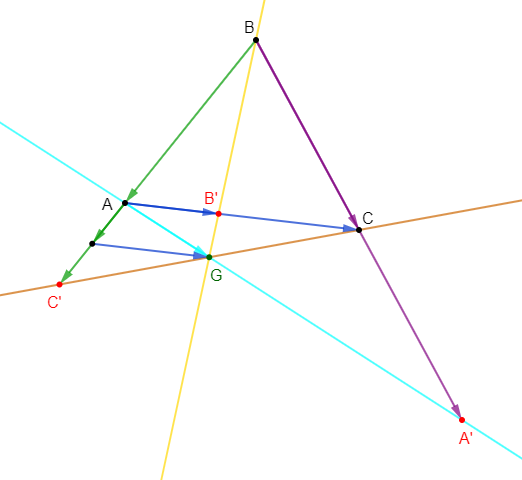
Exercice 8

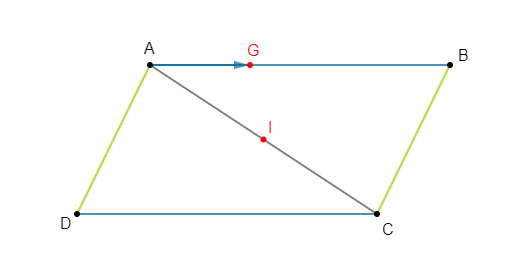
Soit ABCD un parallélogramme, I milieu de [AC]  et  G défini par :
→AG=13→AB
1) Déterminons α  et  β pour que G soit barycentre de (A; α), (B; β)
 
Soit : →AG=13→AB.
 
Alors, en utilisant les propriétés du calcul vectoriel et en introduisant le point G dans le vecteur →AB, par la relation de Chasles, on obtient :
 
→AG=13→AB⇔3→AG=→AB⇔3→AG−→AB=→0⇔3→AG−(→AG+→GB)=→0⇔3→AG−→AG−→GB=→0⇔2→AG+→BG=→0
 
Ainsi, on a : 2→AG+→BG=→0
 
Par conséquent, G est le barycentre du système {(A, 2); (B; 1)}
 
D'où, α=2  et  β=1
 
2) Donnons les coordonnées de A, B, C, D, I,  et  G dans le repère (A; →AC, →AD)
 
En effet, dans ce repère, on a :
 
A est origine du repère, →AC  et  →AD sont les vecteurs de base.
 
Donc, on a :
A(00), C(10)  et  D(01)
Pour déterminer les coordonnées de B dans ce repère, il suffit d'exprimer →AB en fonction de →AC  et  →AD.
 
On a :
→AB=→AC+→CB(1)
Or, ABCD est un parallélogramme. Donc,
→CB=→DA
Ainsi, en remplaçant →CB par →DA, dans la relation (1), on obtient :
 
→AB=→AC+→CB=→AC+→DA=→AC−→AD
 
D'où, →AB=→AC−→AD
 
Par conséquent,
B(1−1)
Soit I milieu de [AC].
 
Alors, on a : →AI=12→AC
 
D'où,
I(120)
On a : →AG=13→AB
 
Or, →AB=→AC−→AD
 
Par conséquent, →AG=13→AC−13→AD
 
D'où,
G(13−13)
3) Donnons les coordonnées de A, B, C, D, I,  et  G dans le repère (B; →BD, →BC)
 
En effet, dans ce repère, B est l'origine, →BD  et  →BC sont les vecteurs de base.
 
Ainsi, on a :
B(00), D(10)  et  C(01)
Pour déterminer les coordonnées de A dans ce repère, il suffit d'exprimer →BA en fonction de →BD  et  →BC.
 
Soit alors :
→BA=→BD+→DA(2)
Comme, ABCD est un parallélogramme alors, on a :
→DA=→CB
Ainsi, dans la relation (2), en remplaçant →DA par →CB, on obtient :
 
→BA=→BD+→DA=→BD+→CB=→BD−→BC
 
Donc, →BA=→BD−→BC
 
D'où,
A(1−1)
On a : I milieu de [AC].
 
Or, ABCD est un parallélogramme.
 
Par conséquent, I est aussi milieu de [BD].
 
D'où, →BI=12→BD
 
Ainsi,
I(120)
G étant le barycentre de (A; 2)  et  (B; 1) alors, d'après la propriété caractéristique, on a :
→BG=23→BA
Or, →BA=→BD−→BC
 
Donc, →BG=23→BD−23→BC
 
Par conséquent,
G(23−23)
4) Donnons les coordonnées de A,  B, C, D, I,  et  G dans le repère (A; →AB, →AD)
 
Dans ce repère, A est l'origine, →AB  et  →AD sont les vecteurs de base.
 
Par conséquent,
A(00), B(10)  et  D(01)
Pour déterminer les coordonnées de C dans ce repère, il suffit d'exprimer →AC en fonction de →AB  et  →AD.
 
On a :
→AC=→AD+→DC(3)
Or, ABCD est un parallélogramme. Donc,
→DC=→AB
Ainsi, en remplaçant →DC par →AB, dans la relation (3), on obtient :
 
→AC=→AD+→DC=→AD+→AB
 
D'où, →AC=→AB+→AD
 
Par conséquent,
C(11)
Soit I milieu de [AC].
 
Alors, on a :
→AI=12→AC
Or, →AC=→AB+→AD
 
Par suite, →AI=12→AB+12→AD
 
D'où,
I(1212)
G étant défini par :
→AG=13→AB
Alors,
G(130)

 

 

Exercice 9

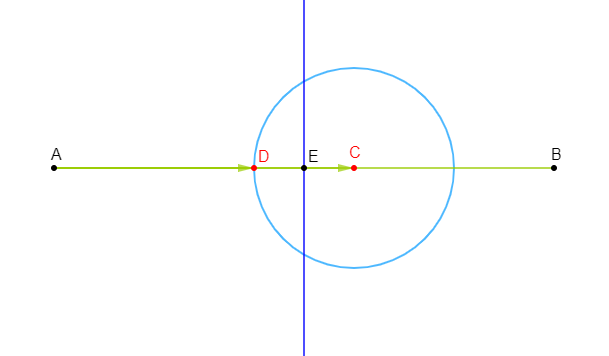
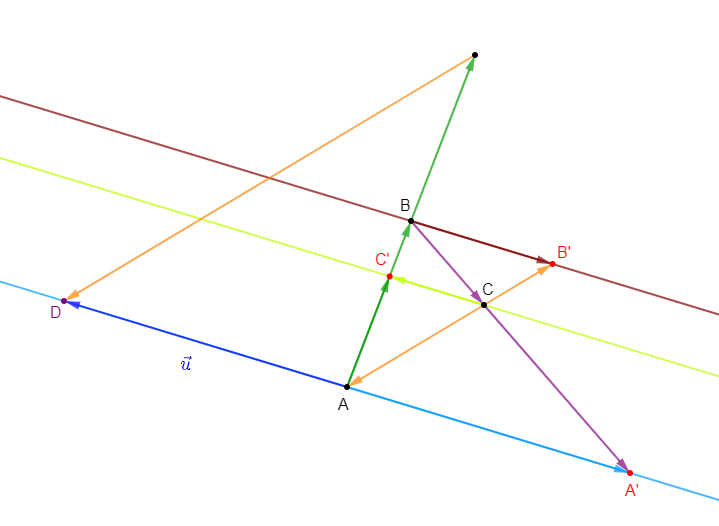
On donne deux points A  et  B tels que AB=10
 
Soit C barycentre de {(A; 2), (B; 3)}  et  D barycentre de {(A; 3), (B; 2)}
 
1) Construisons C  et  D.
 
En effet, soit C barycentre de (A, 2)  et  (B, 3) alors, pour tout point M du plan, d'après la propriété caractéristique, on a :
→MC=2→MA+3→MB2+3
Donc, en remplaçant M par A, on obtient :
→AC=35→AB
De la même manière, soit D barycentre de (A, 3)  et  (B, 2) alors, pour tout point M du plan, d'après la propriété caractéristique, on a :
→MD=3→MA+2→MB3+2
Ainsi, en remplaçant M par A, on trouve :
→AD=25→AB
Plaçons alors les points C  et  D tels que :
→AC=35→AB et →AD=25→AB
2) Démontrons que [AB]  et  [CD] ont même milieu noté E.
 
En effet, comme C est barycentre de {(A; 2), (B; 3)}  et  D barycentre de {(A; 3), (B; 2)} alors, on a les relations vectorielles suivantes :
2→AC+3→BC=→0(1)
3→AD+2→BD=→0(2)
Ainsi, en additionnant, membre à membre les relations (1)  et  (2), on obtient :
2→AC+3→BC+3→AD+2→BD=→0 (3)
Soit alors E le milieu de [AB].
 
Donc, on a :
→AE+→BE=→0
Montrons alors que E est aussi milieu de [CD].
 
En effet, par la relation de Chasles, en introduisant le point E dans l'égalité (3), on obtient :
 
2→AC+3→BC+3→AD+2→BD=→0⇔2(→AE+→EC)+3(→BE+→EC)+3(→AE+→ED)+2(→BE+→ED)=→0⇔2→AE+2→EC+3→BE+3→EC+3→AE+3→ED+2→BE+2→ED=→0⇔5→AE+5→EC+5→BE+5→ED=→0⇔5→AE+5→BE+5→EC+5→ED=→0⇔5(→AE+→BE⏟=→0)+5→EC+5→ED=→0⇔5→EC+5→ED=→0⇔5(→EC+→ED)=→0⇔→EC+→ED=→0
 
D'où, →EC+→ED=→0
 
Ce qui prouve que E est milieu de [CD].
 
3) Déterminons l'ensemble des points M du plan tels que ‖
 
En effet, comme C est barycentre de \{(A\;;\ 2)\;,\ (B\;;\ 3)\} alors, d'après la propriété caractéristique, on a :
2\overrightarrow{MA}+3\overrightarrow{MB}=5\overrightarrow{MC}
Donc, dans la relation (4), en remplaçant 2\overrightarrow{MA}+3\overrightarrow{MB} par 5\overrightarrow{MC}, on obtient :
 
\begin{array}{rcl}\|2\overrightarrow{MA}+3\overrightarrow{MB}\|=10&\Leftrightarrow&\|5\overrightarrow{MC}\|=10\\\\&\Leftrightarrow&5\|\overrightarrow{MC}\|=10\\\\&\Leftrightarrow&\|\overrightarrow{MC}\|=\dfrac{10}{5}\\\\&\Leftrightarrow&\|\overrightarrow{MC}\|=2\end{array}
 
D'où, \boxed{\|\overrightarrow{MC}\|=2}
 
Cela représente alors le cercle de centre C et de rayon 2.
 
Ainsi, l'ensemble des points M du plan tels que \|2\overrightarrow{MA}+3\overrightarrow{MB}\|=10 est le cercle de centre C et de rayon 2.
 
4) Déterminons l'ensemble des points M du plan tels que \|2\overrightarrow{MA}+3\overrightarrow{MB}\|=\|3\overrightarrow{MA}+2\overrightarrow{MB}\|\qquad\ (5)
 
En effet, comme C est barycentre de \{(A\;;\ 2)\;,\ (B\;;\ 3)\}\ et \ D barycentre de \{(A\;;\ 3)\;,\ (B\;;\ 2)\} alors, d'après la propriété caractéristique, on a :
2\overrightarrow{MA}+3\overrightarrow{MB}=5\overrightarrow{MC}
3\overrightarrow{MA}+2\overrightarrow{MB}=5\overrightarrow{MD}
Par suite, dans la relation (5), en remplaçant 2\overrightarrow{MA}+3\overrightarrow{MB} par 5\overrightarrow{MC}\ et \ 3\overrightarrow{MA}+2\overrightarrow{MB} par 5\overrightarrow{MD}, on trouve :
 
\begin{array}{rcl}\|2\overrightarrow{MA}+3\overrightarrow{MB}\|=\|3\overrightarrow{MA}+2\overrightarrow{MB}\|&\Leftrightarrow&\|5\overrightarrow{MC}\|=\|5\overrightarrow{MD}\|\\\\&\Leftrightarrow&5\|\overrightarrow{MC}\|=5\|\overrightarrow{MD}\|\\\\&\Leftrightarrow&\|\overrightarrow{MC}\|=\|\overrightarrow{MD}\|\end{array}
 
Donc, \boxed{\|\overrightarrow{MC}\|=\|\overrightarrow{MD}\|}
 
Ce qui caractérise alors la médiatrice du segment [CD].
 
Ainsi, l'ensemble des points M du plan tels que \|2\overrightarrow{MA}+3\overrightarrow{MB}\|=\|3\overrightarrow{MA}+2\overrightarrow{MB}\| est la médiatrice du segment [CD].
 
C'est donc la droite perpendiculaire à la droite (CD) et passant par le milieu E de [CD].

 
 

Exercice 10

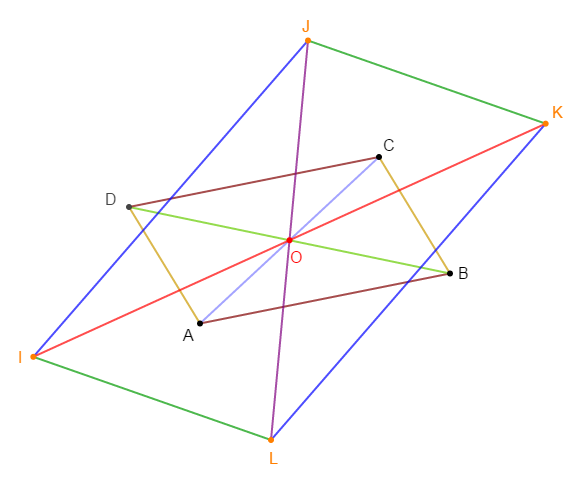
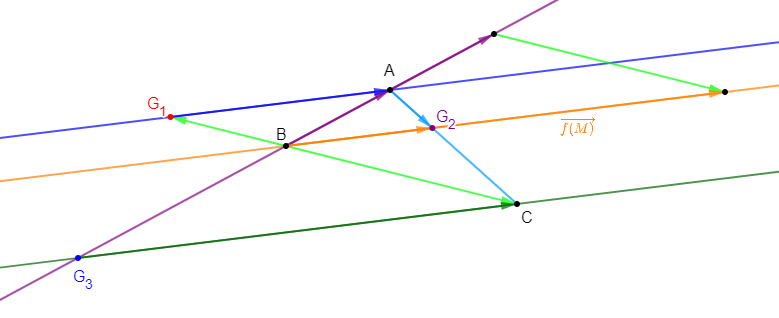
ABCD est un parallélogramme de centre O.
 
1) Définissons vectoriellement et plaçons les points I\;,\ J\;,\ K\ et \ L
 
En effet, on sait que si G est barycentre de (N\;;\ \alpha)\ et \ (P\;;\ \beta) alors, pour tout point M du plan, on a : \alpha\overrightarrow{MN}+\beta\overrightarrow{MP}=(\alpha +\beta)\overrightarrow{MG}
Ce qui donne :
\overrightarrow{MG}=\dfrac{\alpha\overrightarrow{MN}+\beta\overrightarrow{MP}}{\alpha+\beta}
Ainsi, nous allons appliquer cette propriété dans les cas suivants :
 
Soit I barycentre de (A\;,\ 5)\ et \ (B\;,\ -2) alors, d'après la propriété caractéristique, on a :
\overrightarrow{AI}=-\dfrac{2}{3}\overrightarrow{AB}
Soit J barycentre de (B\;,\ 1) et (C\;,\ -2) alors, d'après la propriété caractéristique, on a :
\overrightarrow{BJ}=2\overrightarrow{BC}
Soit K le barycentre de (C\;,\ -5) et (D\;,\ 2) alors, d'après la propriété caractéristique, on a :
\overrightarrow{CK}=-\dfrac{2}{3}\overrightarrow{CD}
Soit L le barycentre de (D\;,\ -1) et (A\;,\ 2) alors, d'après la propriété caractéristique, on a :
\overrightarrow{DL}=2\overrightarrow{DA}
2) Démontrons que IJKL est un parallélogramme de centre O.
 
En sommant membre à membre les égalités du résultat de 1), on obtient :
\overrightarrow{AI}+\overrightarrow{BJ}+\overrightarrow{CK}+\overrightarrow{DL}=-\dfrac{2}{3}\overrightarrow{AB}+2\overrightarrow{BC}-\dfrac{2}{3}\overrightarrow{CD}+2\overrightarrow{DA}
Or, ABCD parallélogramme donc, \overrightarrow{CD}=-\overrightarrow{AB}\ et \ \overrightarrow{DA}=-\overrightarrow{BC}
 
Par suite,
 
\begin{array}{rcl} \overrightarrow{AI}+\overrightarrow{BJ}+\overrightarrow{CK}+\overrightarrow{DL}&=&-\dfrac{2}{3}\overrightarrow{AB}+2\overrightarrow{BC}-\dfrac{2}{3}\overrightarrow{CD}+2\overrightarrow{DA}\\\\&=&-\dfrac{2}{3}\overrightarrow{AB}+2\overrightarrow{BC}+\dfrac{2}{3}\overrightarrow{AB}-2\overrightarrow{BC}\\\\&=&-\dfrac{2}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AB}+2\overrightarrow{BC}-2\overrightarrow{BC}\\\\&=&\vec{0}\end{array}
 
Ainsi, \overrightarrow{AI}+\overrightarrow{BJ}+\overrightarrow{CK}+\overrightarrow{DL}=\vec{0}
 
En introduisant le point O, on obtient :
 
\begin{array}{rcl} \overrightarrow{AI}+\overrightarrow{BJ}+\overrightarrow{CK}+\overrightarrow{DL}=\vec{0}&\Leftrightarrow&\overrightarrow{AO}+\overrightarrow{OI}+\overrightarrow{BO}+\overrightarrow{OJ}+\overrightarrow{CO}+\overrightarrow{OK}\overrightarrow{DO}+\overrightarrow{OL}=\vec{0}\\\\&\Leftrightarrow&\underbrace{\overrightarrow{AO}+\overrightarrow{BO}+\overrightarrow{CO}+\overrightarrow{DO}}_{=\vec{0}}+\overrightarrow{OI}+\overrightarrow{OJ}+\overrightarrow{OK}+\overrightarrow{OL}=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{OI}+\overrightarrow{OJ}+\overrightarrow{OK}+\overrightarrow{OL}=\vec{0}\end{array}
 
Par conséquent, \overrightarrow{OI}+\overrightarrow{OJ}+\overrightarrow{OK}+\overrightarrow{OL}=\vec{0}
 
Ce qui démontre que IJKL est un parallélogramme de centre O.
 

 

Exercice 11

Soit ABC un triangle, A' le barycentre des points pondérés (B\;,\ -1)\ et \ (C\;,\ 2)
 
B' le barycentre de (A\;,\ 3)\ et \ (C\;,\ 2)\ et \ C' le barycentre de (A\;,\ 3)\ et \ (B\;,\ -1).
 
1) Plaçons les points A'\;,\ B'\ et \ C'.
 
En effet, A' étant le barycentre des points pondérés (B\;,\ -1)\ et \ (C\;,\ 2) alors, d'après la propriété caractéristique, on a :
 
Pour tout point M du plan,
\overrightarrow{MA'}=\dfrac{-\overrightarrow{MB}+2\overrightarrow{MC}}{-1+2}
Donc, en remplaçant M par B, on obtient :
\overrightarrow{BA'}=2\overrightarrow{BC}
De même, comme B' est le barycentre de (A\;,\ 3)\ et \ (C\;,\ 2) alors, d'après la propriété caractéristique, on a :
 
Pour tout point M du plan,
\overrightarrow{MB'}=\dfrac{3\overrightarrow{MA}+2\overrightarrow{MC}}{3+2}
Ainsi, en remplaçant M par A, on obtient :
\overrightarrow{AB'}=\dfrac{2}{5}\overrightarrow{AC}
De la même manière, C' étant le barycentre de (A\;,\ 3)\ et \ (B\;,\ -1) alors, en appliquant la propriété caractéristique, on a :
 
Pour tout point M du plan,
\overrightarrow{MC'}=\dfrac{3\overrightarrow{MA}-\overrightarrow{MB}}{3-1}
Alors, en remplaçant M par B, on obtient :
\overrightarrow{BC'}=\dfrac{3}{2}\overrightarrow{BA}
Donc, nous allons placer les points A'\;,\ B'\ et \ C' tels que :
\overrightarrow{BA'}=2\overrightarrow{BC}\;,\quad\overrightarrow{AB'}=\dfrac{2}{5}\overrightarrow{AC}\quad\text{ et }\quad\overrightarrow{BC'}=\dfrac{3}{2}\overrightarrow{BA}
 

 
2) Soit G le barycentre de (A\;,\ 3)\;,\ (B\;,\ -1)\ et \ (C\;,\ 2). 
 
Montrons que :
3\overrightarrow{GA}+\overrightarrow{GA'}=\vec{0}
en effet, on sait que  A' est le barycentre de (B\;,\ -1)\ et \ (C\;,\ 2). 
 
Donc, d'après la propriété d'associativité du barycentre, G est barycentre de (A\;,\ 3)\ et \ (A'\;,\ 1).
 
Ce qui se traduit par la relation vectorielle suivante :
3\overrightarrow{GA}+\overrightarrow{GA'}=\vec{0}
En déduisons que G est un point de (AA').
 
Par la relation de Chasles, introduisons le point A dans le vecteur \overrightarrow{GA'}.
 
On obtient alors :
 
\begin{array}{rcl}3\overrightarrow{GA}+\overrightarrow{GA'}=\vec{0}&\Leftrightarrow&3\overrightarrow{GA}+\overrightarrow{GA}+\overrightarrow{AA'}=\vec{0}\\\\&\Leftrightarrow&4\overrightarrow{GA}=-\overrightarrow{AA'}\\\\&\Leftrightarrow&4\overrightarrow{AG}=\overrightarrow{AA'}\\\\&\Leftrightarrow&\overrightarrow{AG}=\dfrac{1}{4}\overrightarrow{AA'}\end{array}
 
Donc, \boxed{\overrightarrow{AG}=\dfrac{1}{4}\overrightarrow{AA'}}
 
D'où, les points A\;,\ G\ et \ A' sont alignés.
 
Par conséquent, G est un point de (AA').
 
3) Montrons que les droites (AA')\;,\ (BB')\ et \ (CC') sont concourantes.
 
De la même manière que dans la question 2\;), considérons le barycentre partiel B' des points pondérés (A\;,\ 3)\ et \ (C\;,\ 2).
 
Alors, d'après la propriété d'associativité du barycentre, G est barycentre de (B'\;,\ 5)\ et \ (B\;,\ -1).
 
Ainsi, d'après la propriété caractéristique, on obtient :
\overrightarrow{BG}=\dfrac{5}{4}\overrightarrow{BB'}
Ce qui signifie que les points B\;,\ G\ et \ B' sont alignés.
 
D'où, G\in\;(BB').
 
Par ailleurs, C' étant le barycentre des points pondérés (A\;,\ 3)\ et \ (B\;,\ -1) alors, d'après la propriété d'associativité du barycentre, G est barycentre de (C'\;,\ 2)\ et \ (C\;,\ 2).
 
Les coefficients de C\ et \ C' étant les mêmes alors, G est le milieu de [CC'].
 
Par conséquent, G est un point de la droite (CC').
 
Ainsi, on a :
G\in\;(AA')\;,\ G\in\;(BB')\;,\ G\in\;(CC')
D'où, \boxed{G\in\;(AA')\cap(BB')\cap(CC')}
 
Ce qui montre que (AA')\;,\ (BB')\ et \ (CC') sont concourantes au point G.

Exercice 12

Soit ABC un triangle. Soient I\ et \ J les points définis par :
\overrightarrow{AI}=\dfrac{3}{4}\overrightarrow{AB}\quad \text{ et }\quad \overrightarrow{AJ}=\dfrac{2}{3}\overrightarrow{AC}
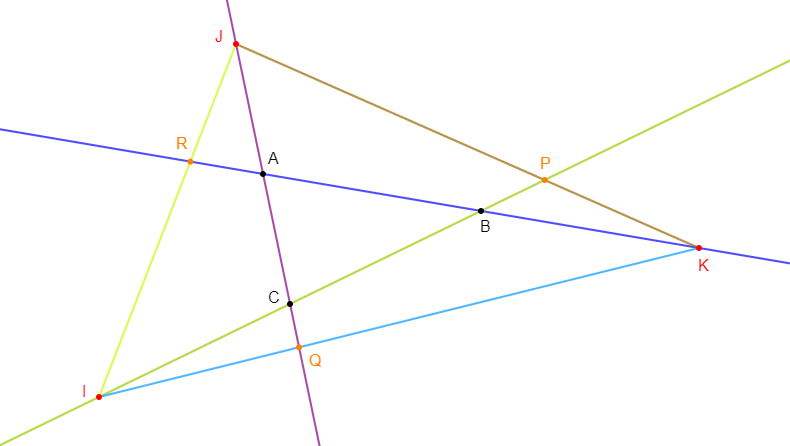
Les droites (BJ)\ et \ (CI) se coupent en G. La droite (AG) coupe (BC) en K.
 
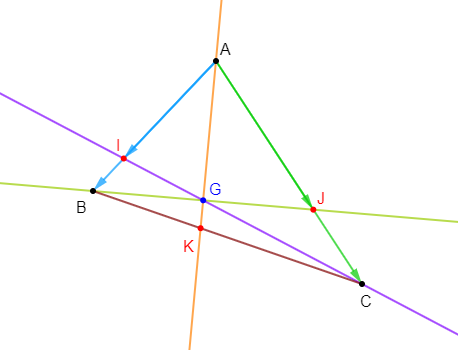
1) Faisons une figure.

 

 
2) Trouvons les réels a\;,\ b\ et \ c tels que I soit le barycentre de \{(A\;,\ a)\;;\ (B\;,\ b)\}\ et \ J le barycentre du système \{(A\;,\ a)\;;\ (C\;,\ c)\}.
 
On a :
 
\begin{array}{rcl}\overrightarrow{AI}=\dfrac{3}{4}\overrightarrow{AB}&\Leftrightarrow&4\overrightarrow{AI}=3\overrightarrow{AB}\\\\&\Leftrightarrow&4\overrightarrow{AI}-3\overrightarrow{AB}=\vec{0}\\\\&\Leftrightarrow&4\overrightarrow{AI}-3\left(\overrightarrow{AI}+\overrightarrow{IB}\right)=\vec{0}\\\\&\Leftrightarrow&4\overrightarrow{AI}-3\overrightarrow{AI}-3\overrightarrow{IB}=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{AI}-3\overrightarrow{IB}=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{AI}+3\overrightarrow{BI}=\vec{0}\end{array}
 
Ainsi, \boxed{\overrightarrow{AI}+3\overrightarrow{BI}=\vec{0}}
 
D'où, I est le barycentre de \{(A\;,\ 1)\;;\ (B\;,\ 3)\}
 
Par ailleurs, soit :
 
\begin{array}{rcl}\overrightarrow{AJ}=\dfrac{2}{3}\overrightarrow{AC}&\Leftrightarrow&3\overrightarrow{AJ}=2\overrightarrow{AC}\\\\&\Leftrightarrow&3\overrightarrow{AJ}-2\overrightarrow{AC}=\vec{0}\\\\&\Leftrightarrow&3\overrightarrow{AJ}-2\left(\overrightarrow{AJ}+\overrightarrow{JC}\right)=\vec{0}\\\\&\Leftrightarrow&3\overrightarrow{AJ}-2\overrightarrow{AJ}-2\overrightarrow{JC}=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{AJ}-2\overrightarrow{JC}=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{AJ}+2\overrightarrow{CJ}=\vec{0}\end{array}
 
Ainsi, \boxed{\overrightarrow{AJ}+2\overrightarrow{CJ}=\vec{0}}
 
Ce qui signifie que J est le barycentre de \{(A\;,\ 1)\;;\ (C\;,\ 2)\}
 
Donc, \boxed{a=1\;,\ b=3\;,\ c=2}
 
3) Montrons que le barycentre du système \{(A\;,\ 1)\;;\ (B\;,\ 3)\;;\ (C\;,\ 2)\} est le point G.
 
En effet, considérons un point O barycentre du système \{(A\;,\ 1)\;;\ (B\;,\ 3)\;;\ (C\;,\ 2)\}.
 
D'après le résultat de la question 2\;)\;,\ I est le barycentre de \{(A\;,\ 1)\;;\ (B\;,\ 3)\}.
 
Donc, d'après la propriété d'associativité du barycentre, O est le barycentre du système \{(I\;,\ 4)\;;\ (C\;,\ 2)\}.
 
D'où, O\;,\ I\ et \ C sont alignés.
 
Par conséquent, O\in(CI).
 
De la même manière, J étant le barycentre de \{(A\;,\ 1)\;;\ (C\;,\ 2)\} alors, d'après la propriété d'associativité du barycentre, O est le barycentre du système \{(J\;,\ 3)\;;\ (B\;,\ 3)\}.
 
Ce qui signifie que O est le milieu de [BJ].
 
Par conséquent, O\in(BJ).
 
Ainsi, on a :
O\in(CI)\;,\ O\in(BJ)
Donc, \boxed{O\in(CI)\cap(BJ)}
 
Ce qui signifie que les droites (CI)\ et \ (BJ) sont sécantes en O.
 
Or, par hypothèse, les droites (BJ)\ et \ (CI) se coupent en G.
 
Par conséquent, O=G, c'est-à-dire ; O\ et \ G sont confondus.
 
Ce qui montre que G est le barycentre du système \{(A\;,\ 1)\;;\ (B\;,\ 3)\;;\ (C\;,\ 2)\}.
 
En déduisons que K est le barycentre de (B\;,\ 3)\ et \ (C\;,\ 2).
 
En effet, comme la droite (AG) coupe la droite (BC) en K alors, on a :
 
d'une part A\;,\ G\;,\ K alignés, d'autre part B\;,\ C\;,\ K alignés.
 
Ainsi :
 
K est barycentre du système \{(B\;,\ \beta)\;;\ (C\;,\ \gamma)\} 
 
G est barycentre du système \{(A\;,\ 1)\;;\ (K\;,\ \beta+\gamma)\}
 
Par suite, G est le barycentre du système \{(A\;,\ 1)\;;\ (B\;,\ \beta)\;;\ (C\;,\ \gamma)\}
 
Or, on vient juste de montrer que G est le barycentre du système \{(A\;,\ 1)\;;\ (B\;,\ 3)\;;\ (C\;,\ 2)\}.
 
Par conséquent, \boxed{\beta=3\;,\ \gamma=2}
 
D'où, K est le barycentre de (B\;,\ 3)\ et \ (C\;,\ 2).
 
Donnons la position de K sur la droite (BC).
 
En effet, K étant le barycentre du système \{(B\;,\ 3)\;;\ (C\;,\ 2)\} alors, d'après la propriété caractéristique, on a :
\overrightarrow{BK}=\dfrac{2}{5}\overrightarrow{BC}
Par conséquent, \boxed{K\in[BC]}

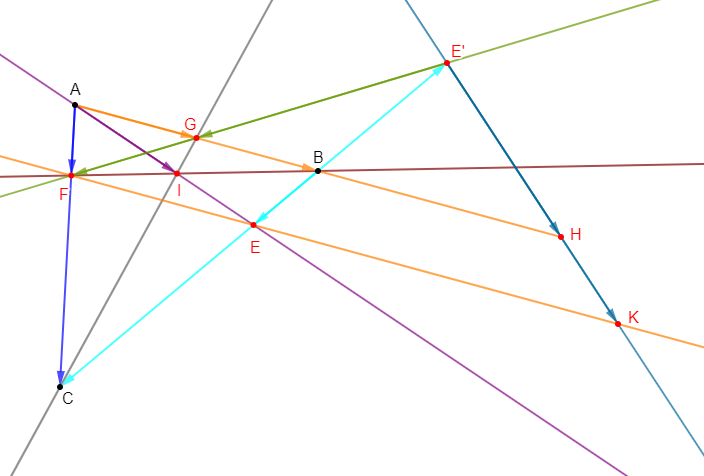
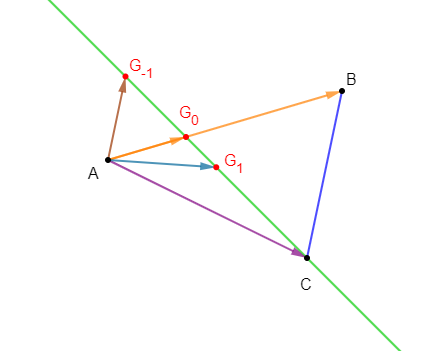
Exercice 13

Soit ABC un triangle quelconque.
 
1) Construisons les barycentres suivants :
 
Soit G le barycentre de (A\;,\ 3)\ et \ (B\;,\ 3).
 
Comme les coefficients de pondération de A\ et \ B sont les mêmes alors, G est le milieu de [AB].
 
D'où,
\overrightarrow{AG}=\dfrac{1}{2}\overrightarrow{AB}
Soit E le barycentre de (B\;,\ 3)\ et \ (C\;,\ 1) alors, d'après la propriété caractéristique, on a :
\overrightarrow{BE}=\dfrac{1}{4}\overrightarrow{BC}
Soit F le barycentre de (A\;,\ 3)\ et \ (C\;,\ 1) alors, en appliquant la propriété caractéristique, on obtient :
\overrightarrow{AF}=\dfrac{1}{4}\overrightarrow{AC}
2) Soit I le barycentre de (A\;,\ 3)\;,\ (B\;,\ 3)\ et \ (C\;,\ 1).
 
Démontrons que les points A\;,\ I\ et \ E sont alignés.
 
On sait que E est le barycentre de (B\;,\ 3)\ et \ (C\;,\ 1).
 
Donc, en appliquant la propriété d'associativité du barycentre, on obtient : I barycentre de (A\;,\ 3)\ et \ (E\;,\ 4).
 
D'où, les points A\;,\ I\ et \ E sont alignés.
 
Démontrons que les points B\;,\ I\ et \ F sont alignés.
 
F étant le barycentre de (A\;,\ 3)\ et \ (C\;,\ 1) alors, d'après la propriété d'associativité du barycentre, I est barycentre de (F\;,\ 4)\ et \ (B\;,\ 3).
 
Par conséquent, les points B\;,\ I\ et \ F sont alignés.
 
Démontrons que les points C\;,\ I et G sont alignés.
 
Comme G est le barycentre de (A\;,\ 3)\ et \ (B\;,\ 3) alors, d'après la propriété d'associativité du barycentre, I est le barycentre de (G\;,\ 6)\ et \ (C\;,\ 1).
 
On peut en déduire que les droites (AE)\;,\ (BF)\ et \ (CG) sont concourantes en I.
 
En effet, on a : I\in(AE)\;,\ I\in(BF)\ et \ I\in(CG).
 
D'où, \boxed{I\in(AE)\cap(BF)\cap(CG)}
 
Par conséquent, les droites (AE)\;,\ (BF)\ et \ (CG) sont concourantes en I.
 
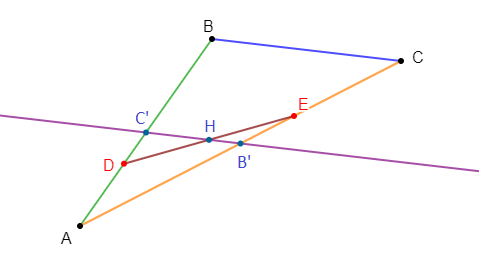
3) Construisons le barycentre E' de (B\;,\ 3)\ et \ (C\;,\ -1).
 
D'après la propriété caractéristique, on a :
\overrightarrow{BE'}=-\dfrac{1}{2}\overrightarrow{BC}
Exprimons le vecteur \overrightarrow{E'G} en fonction des vecteurs \overrightarrow{AB}\ et \ \overrightarrow{AC}.
 
Par la relation de Chasles, en introduisant le point B dans le vecteur \overrightarrow{E'G}, on obtient :
\overrightarrow{E'G}=\overrightarrow{E'B}+\overrightarrow{BG}\qquad(1)
Or, G milieu de [AB] donc,
\overrightarrow{BG}=\dfrac{1}{2}\overrightarrow{BA}
Par ailleurs, on a :
\overrightarrow{BE'}=-\dfrac{1}{2}\overrightarrow{BC}\ \Rightarrow\ \overrightarrow{E'B}=\dfrac{1}{2}\overrightarrow{BC}
La relation (1) devient alors :
\overrightarrow{E'G}=\dfrac{1}{2}\overrightarrow{BC}+\dfrac{1}{2}\overrightarrow{BA}
Par la relation de Chasles, introduisons le point A dans le vecteur \overrightarrow{BC}.
 
On obtient alors :
 
\begin{array}{rcl}\overrightarrow{E'G}=\dfrac{1}{2}\overrightarrow{BC}+\dfrac{1}{2}\overrightarrow{BA}&\Leftrightarrow&\overrightarrow{E'G}=\dfrac{1}{2}\left(\overrightarrow{BA}+\overrightarrow{AC}+\overrightarrow{BA}\right)\\\\&\Leftrightarrow&\overrightarrow{E'G}=\dfrac{1}{2}\left(2\overrightarrow{BA}+\overrightarrow{AC}\right)\\\\&\Leftrightarrow&\overrightarrow{E'G}=\overrightarrow{BA}+\dfrac{1}{2}\overrightarrow{AC}\\\\&\Leftrightarrow&\overrightarrow{E'G}=-\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\end{array}
 
D'où, \boxed{\overrightarrow{E'G}=-\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}}
 
Exprimons le vecteur \overrightarrow{GF} en fonction des vecteurs \overrightarrow{AB}\ et \ \overrightarrow{AC}.
 
Par la relation de Chasles, introduisons le point A dans le vecteur \overrightarrow{GF}.
 
On obtient alors :
\overrightarrow{GF}=\overrightarrow{GA}+\overrightarrow{AF}\qquad(2)
Or, on a : \overrightarrow{AG}=\dfrac{1}{2}\overrightarrow{AB} donc,
\overrightarrow{GA}=-\dfrac{1}{2}\overrightarrow{AB}
Aussi, on a :
\overrightarrow{AF}=\dfrac{1}{4}\overrightarrow{AC}
Ainsi, en remplaçant \overrightarrow{GA}\ et \ \overrightarrow{AF} par leur expression, dans la relation (2), on obtient :
 
\begin{array}{rcl}\overrightarrow{GF}&=&\overrightarrow{GA}+\overrightarrow{AF}\\\\&=&-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\end{array}
 
D'où, \boxed{\overrightarrow{GF}=-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}}
 
En déduisons que E'\;,\ F\ et \ G sont alignés.
 
En multipliant le vecteur \overrightarrow{GF} par 2, on trouve :
 
\begin{array}{rcl}2\times\overrightarrow{GF}&=&2\left(-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\right)\\\\&=&-\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\\\\&=&\overrightarrow{E'G}\end{array}
 
Ainsi, \boxed{\overrightarrow{E'G}=2\overrightarrow{GF}}
 
Par conséquent, les points E'\;,\ F\ et \ G sont alignés.
 
4) Montrons que les droites (EF)\ et \ (AB) sont parallèles.
 
En effet, (AC)\ et \ (BC) sont deux droites sécantes en C.
 
F\in[AC]\ et \ E\in[BC]
 
Or, d'après la question 1\;), on a :
\overrightarrow{BE}=\dfrac{1}{4}\overrightarrow{BC}
\overrightarrow{AF}=\dfrac{1}{4}\overrightarrow{AC}
Donc, d'après la forme vectorielle de la réciproque du théorème de Thalès, les droite (EF)\ et \ (AB) sont parallèles.
 
Méthode des longueurs
 
D'après la question 1\;), on a :
\left\lbrace\begin{array}{rcl}\overrightarrow{BE}&=&\dfrac{1}{4}\overrightarrow{BC}\\\\\overrightarrow{AF}&=&\dfrac{1}{4}\overrightarrow{AC}\end{array}\right.\quad \Rightarrow\quad \left\lbrace\begin{array}{rcl}\dfrac{\|\overrightarrow{BE}\|}{\|\overrightarrow{BC}\|}&=&\dfrac{1}{4}\\\\\dfrac{\|\overrightarrow{AF}\|}{\|\overrightarrow{AC}\|}&=&\dfrac{1}{4}\end{array}\right.
Par conséquent, on obtient :
\dfrac{\|\overrightarrow{BE}\|}{\|\overrightarrow{BC}\|}=\dfrac{\|\overrightarrow{AF}\|}{\|\overrightarrow{AC}\|}=\dfrac{1}{4}
Ainsi, d'après la réciproque du théorème de Thalès, les droite (EF)\ et \ (AB) sont parallèles.
 
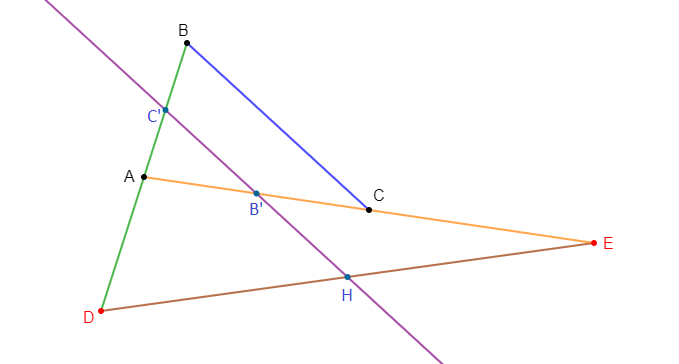
Soit H le symétrique de A par rapport à B\ et \ K le point d'intersection des droites (E'H)\ et \ (EF).
 
Montrer que :
\overrightarrow{E'K}=\dfrac{3}{2}\overrightarrow{E'H}
Comme H est le symétrique de A par rapport à B alors, H\in(AB).
 
Par ailleurs, K étant le point d'intersection des droites (E'H)\ et \ (EF) alors, K\in(EF).
 
Aussi, d'après le résultat de la question 4\;), les droites (EF)\ et \ (AB) sont parallèles.
 
Ce qui revient au même de dire que les droites (FK)\ et \ (GH) sont parallèles.
 
Ainsi, les triangles E'FK\ et \ E'GH sont en position de Thalès.
 
Or, d'après le résultat de la question 3\;), on a :
\overrightarrow{E'G}=2\overrightarrow{GF}
Donc, d'après la forme vectorielle du théorème de Thalès, on a :
\overrightarrow{E'H}=2\overrightarrow{HK}
Par la relation de Chasles, introduisons le point E' dans le vecteur \overrightarrow{HK}.
 
On obtient alors :
 
\begin{array}{rcl}\overrightarrow{E'H}=2\overrightarrow{HK}&\Leftrightarrow&\overrightarrow{E'H}=2\left(\overrightarrow{HE'}+\overrightarrow{E'K}\right)\\\\&\Leftrightarrow&\overrightarrow{E'H}=2\overrightarrow{HE'}+2\overrightarrow{E'K}\\\\&\Leftrightarrow&\overrightarrow{E'H}-2\overrightarrow{HE'}=2\overrightarrow{E'K}\\\\&\Leftrightarrow&\overrightarrow{E'H}+2\overrightarrow{E'H}=2\overrightarrow{E'K}\\\\&\Leftrightarrow&3\overrightarrow{E'H}=2\overrightarrow{E'K}\\\\&\Leftrightarrow&\overrightarrow{E'K}=\dfrac{3}{2}\overrightarrow{E'H}\end{array}
 
D'où, \boxed{\overrightarrow{E'K}=\dfrac{3}{2}\overrightarrow{E'H}}

 

 
 

Exercice 14

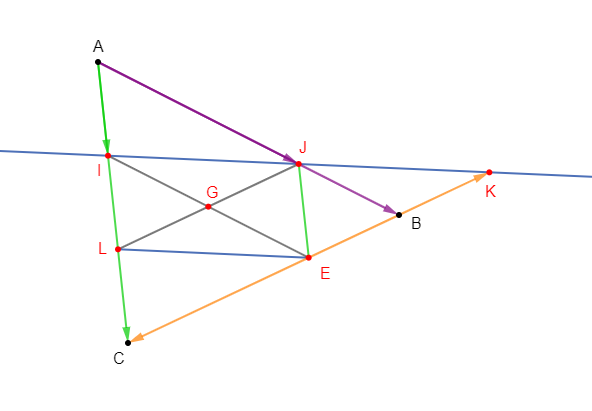
1) Soit ABC un triangle, construisons les points I\;,\ J\ et \ K définis par :
 
-\ I est le barycentre de (A\;,\ 2) et (C\;,\ 1)
 
Alors, d'après la propriété caractéristique, on a :
\overrightarrow{AI}=\dfrac{1}{3}\overrightarrow{AC}
-\ J est le barycentre de (A\;,\ 1) et (B\;,\ 2)
 
Donc, en appliquant la propriété caractéristique, on obtient :
\overrightarrow{AJ}=\dfrac{2}{3}\overrightarrow{AB}
-\ K est le barycentre de (C\;,\ 1) et (B\;,\ -4).
 
Alors, d'après la propriété caractéristique, on a :
\overrightarrow{BK}=-\dfrac{1}{3}\overrightarrow{BC}
2) Exprimons B comme barycentre de (K\;,\ \alpha)\ et \ (C\;,\ 1)\;;\ (\alpha étant un réel à déterminer.)
 
D'après la question 1\;), on a : K barycentre de (C\;,\ 1) et (B\;,\ -4).
 
Ce qui se traduit par :
\overrightarrow{CK}-4\overrightarrow{BK}=\vec{0}
Ainsi, par la relation de Chasles, en introduisant le point B dans le vecteur \overrightarrow{CK}, on obtient :
 
\begin{array}{rcl}\overrightarrow{CK}-4\overrightarrow{BK}=\vec{0}&\Leftrightarrow&\overrightarrow{CB}+\overrightarrow{BK}-4\overrightarrow{BK}=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{CB}-3\overrightarrow{BK}=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{CB}+3\overrightarrow{KB}=\vec{0}\end{array}
 
D'où, \boxed{\overrightarrow{CB}+3\overrightarrow{KB}=\vec{0}}
 
Ce qui signifie que B est le barycentre de (K\;,\ 3)\ et \ (C\;,\ 1)
 
3) Déterminons le barycentre de (A\;,\ 2)\;,\ (K\;,\ 3)\ et \ (C\;,\ 1)
 
D'après le résultat de la question 2\;), on a : B barycentre de (K\;,\ 3)\ et \ (C\;,\ 1).
 
Donc, en appliquant la propriété d'associativité du barycentre, on a : le barycentre de (A\;,\ 2)\;,\ (K\;,\ 3)\ et \ (C\;,\ 1) est le même que celui des points pondérés (A\;,\ 2)\ et \ (B\;,\ 4).
 
Par ailleurs, d'après la propriété d'homogénéité, le barycentre reste inchangé si on multiplie ses coefficients par un même réel non nul.
 
Donc, le système \{(A\;,\ 2)\;;\ (B\;,\ 4)\}\ et le système \ \{(A\;,\ 1)\;;\ (B\;,\ 2)\} ont le même barycentre.
 
Or, on sait que J est le barycentre de (A\;,\ 1)\ et \ (B\;,\ 2).
 
Par conséquent, J est le barycentre de (A\;,\ 2)\;,\ (K\;,\ 3)\ et \ (C\;,\ 1).
 
4) Déduisons du 3\;) que I\;,\ J\;,\ K sont alignés.
 
D'après le résultat de la question 3\;), on a : J barycentre de (A\;,\ 2)\;,\ (K\;,\ 3)\ et \ (C\;,\ 1).
 
Or, on sait que I est le barycentre de (A\;,\ 2)\ et \ (C\;,\ 1).
 
Donc, d'après la propriété d'associativité du barycentre, on a : J barycentre de (K\;,\ 3)\ et \ (I\;,\ 3).
 
D'où, les points I\;,\ J\ et \ K sont alignés.
 
K\ et \ I ayant le même coefficient de pondération, J est alors le milieu du segment [IK].
 
5) L étant le milieu de [CI]\ et \ E celui de [KC], démontrons que IJEL est un parallélogramme dont le centre G est l'isobarycentre de A\;,\ B\ et \ C.
 
Considérons le triangle CIK.
 
E milieu de [KC]\ et \ L milieu de [CI] alors, d'après le théorème de la droite des milieux, (IK)\ et \ (LE) sont parallèles et on a :
LE=\dfrac{1}{2}IK
Or, J est le milieu de [IK].
 
Donc,
IJ=\dfrac{1}{2}IK
Par conséquent, \boxed{IJ=LE}
 
Ainsi, le quadrilatère non croisé IJEL est tel que :
\left\lbrace\begin{array}{rcl}(IJ)//(LE)\\\\IJ=LE\end{array}\right.
Par conséquent, IJEL est un parallélogramme.
 
Soit G le centre de IJEL alors, montrons que G est l'isobarycentre de A\;,\ B\ et \ C.
 
En effet, comme G est le centre du parallélogramme IJEL alors, G est l'isobarycentre de I\;,\ J\;,\ E\ et \ L.
 
Donc,
\overrightarrow{GI}+\overrightarrow{GJ}+\overrightarrow{GE}+\overrightarrow{GL}=\vec{0}
Ainsi, par la relation de Chasles, introduisons les points A\;,\ B\ et \ C respectivement dans les vecteurs \overrightarrow{GI}\;,\ \overrightarrow{GJ}\ et \ \overrightarrow{GL}
 
\begin{array}{rcl}\overrightarrow{GI}+\overrightarrow{GJ}+\overrightarrow{GE}+\overrightarrow{GL}=\vec{0}&\Leftrightarrow&\overrightarrow{GA}+\overrightarrow{AI}+\overrightarrow{GB}+\overrightarrow{BJ}+\overrightarrow{GE}+\overrightarrow{GC}+\overrightarrow{CL}=\vec{0}\\\\&=&\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\underbrace{\overrightarrow{BJ}+\overrightarrow{GE}}_{=\vec{0}}+\underbrace{\overrightarrow{AI}+\overrightarrow{CL}}_{=\vec{0}}=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}\end{array}
 
D'où, \boxed{\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}}
 
Ce qui montre que G est le centre de gravité du triangle ABC ou encore l'isobarycentre des points A\;,\ B\ et \ C.

 

Exercice 15

Soit ABC un triangle . On effectue les constructions suivantes : on symétrise A par rapport à B\;,\ B par rapport à C et C par rapport à A ; on obtient respectivement les points K\;,\ I\;,\ J\ (donc un triangle IJK).
 
1) Faisons une figure .

 

 
2) Exprimons chacun des points A\;,\ B\;,\ C comme barycentre des points I\;,\ J\;,\ K
 
-\ Pour le point A, on a :
 
J symétrique de C par rapport à A alors, A est milieu de [CJ].
 
Donc,
\overrightarrow{AJ}+\overrightarrow{AC}=\vec{0}
Ensuite, par la relation de Chasles, en introduisant le point I dans le vecteur \overrightarrow{AC}, on obtient :
\overrightarrow{AJ}+\overrightarrow{AI}+\overrightarrow{IC}=\vec{0}
Or, B\ et \ I sont symétriques par rapport à C. Donc, C est milieu de [IB].
 
Par suite,
\overrightarrow{IC}=\overrightarrow{CB}
Donc, on a :
\overrightarrow{AJ}+\overrightarrow{AI}+\overrightarrow{CB}=\vec{0}
Puis, en utilisant la relation de Chasles dans le vecteur \overrightarrow{CB}, on obtient :
\overrightarrow{CB}=\overrightarrow{CA}+\overrightarrow{AB}
Ainsi, on a :
\overrightarrow{AJ}+\overrightarrow{AI}+\overrightarrow{CA}+\overrightarrow{AB}=\vec{0}
Enfin, \overrightarrow{CA}=\overrightarrow{AJ}\ et \ \overrightarrow{AB}=\dfrac{1}{2}\overrightarrow{AK} du fait que A est milieu de [CJ]\ et \ B est milieu de [AK].
 
Donc, en remplaçant, on obtient :
 
\begin{array}{rcl}\overrightarrow{AJ}+\overrightarrow{AI}+\overrightarrow{CA}+\overrightarrow{AB}=\vec{0}&\Leftrightarrow&\overrightarrow{AJ}+\overrightarrow{AI}+\overrightarrow{AJ}+\dfrac{1}{2}\overrightarrow{AK}=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{AI}+2\overrightarrow{AJ}+\dfrac{1}{2}\overrightarrow{AK}=\vec{0}\\\\&\Leftrightarrow&\dfrac{1}{2}\left(2\overrightarrow{AI}+4\overrightarrow{AJ}+\overrightarrow{AK}\right)=\vec{0}\\\\&\Leftrightarrow&2\overrightarrow{AI}+4\overrightarrow{AJ}+\overrightarrow{AK}=\vec{0}\end{array}
 
D'où, \boxed{2\overrightarrow{AI}+4\overrightarrow{AJ}+\overrightarrow{AK}=\vec{0}}
 
Par conséquent, A est barycentre de (I\;;\ 2)\;,\ (J\;;\ 4)\ et \ (K\;;\ 1).
 
-\ Pour le point B, on a :
 
K est le symétrique de A par rapport à B donc, B est milieu de [AK].
 
Ainsi,
\overrightarrow{BK}+\overrightarrow{BA}=\vec{0}
En procédant de la même que pour le point A, on obtient :
 
\begin{array}{rcl}\overrightarrow{BK}+\overrightarrow{BA}=\vec{0}&\Leftrightarrow&\overrightarrow{BK}+\overrightarrow{BJ}+\overrightarrow{JA}=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{BK}+\overrightarrow{BJ}+\overrightarrow{AC}=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{BK}+\overrightarrow{BJ}+\overrightarrow{AB}+\overrightarrow{BC}=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{BK}+\overrightarrow{BJ}+\overrightarrow{BK}+\dfrac{1}{2}\overrightarrow{BI}=\vec{0}\\\\&\Leftrightarrow&\dfrac{1}{2}\overrightarrow{BI}+\overrightarrow{BJ}+2\overrightarrow{BK}=\vec{0}\\\\&\Leftrightarrow&\dfrac{1}{2}\left(\overrightarrow{BI}+2\overrightarrow{BJ}+4\overrightarrow{BK}\right)=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{BI}+2\overrightarrow{BJ}+4\overrightarrow{BK}=\vec{0}\end{array}
 
Donc, \boxed{\overrightarrow{BI}+2\overrightarrow{BJ}+4\overrightarrow{BK}=\vec{0}}
 
D'où, B est barycentre de (I\;;\ 1)\;,\ (J\;;\ 2)\ et \ (K\;;\ 4).
 
-\ Pour le point C, on a :
 
I symétrique de B par rapport à C alors, C est milieu de [BI].
 
Donc, on a :
\overrightarrow{CI}+\overrightarrow{CB}=\vec{0}
Ainsi, en procédant de la même que pour le point A, on obtient :
 
\begin{array}{rcl}\overrightarrow{CI}+\overrightarrow{CB}=\vec{0}&\Leftrightarrow&\overrightarrow{CI}+\overrightarrow{CK}+\overrightarrow{KB}=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{CI}+\overrightarrow{CK}+\overrightarrow{BA}=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{CI}+\overrightarrow{CK}+\overrightarrow{BC}+\overrightarrow{CA}=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{CI}+\overrightarrow{CK}+\overrightarrow{CI}+\dfrac{1}{2}\overrightarrow{CJ}=\vec{0}\\\\&\Leftrightarrow&2\overrightarrow{CI}+\dfrac{1}{2}\overrightarrow{CJ}+\overrightarrow{CK}=\vec{0}\\\\&\Leftrightarrow&\dfrac{1}{2}\left(4\overrightarrow{CI}+\overrightarrow{CJ}+2\overrightarrow{CK}\right)=\vec{0}\\\\&\Leftrightarrow&4\overrightarrow{CI}+\overrightarrow{CJ}+2\overrightarrow{CK}=\vec{0}\end{array}
 
Ainsi, \boxed{4\overrightarrow{CI}+\overrightarrow{CJ}+2\overrightarrow{CK}=\vec{0}}
 
Par conséquent, C est barycentre de (I\;;\ 4)\;,\ (J\;;\ 1)\ et \ (K\;;\ 2).
 
3) On définit les points P\;,\ Q\;,\ R par :
\overrightarrow{KP}=\dfrac{1}{3}\overrightarrow{KJ}\;,\quad \overrightarrow{IQ}=\dfrac{1}{3}\overrightarrow{IK}\;,\quad \overrightarrow{JR}=\dfrac{1}{3}\overrightarrow{JI}
Montrons que les points P\;,\ Q\;,\ R sont respectivement les points d'intersection des droites (BC)\ et \ (KJ)\;,\ (AC)\ et \ (KI)\;,\ (AB)\ et \ (JI).
 
Soit : \overrightarrow{KP}=\dfrac{1}{3}\overrightarrow{KJ}
 
Alors, P appartient à la droite (KJ) et on a :
 
\begin{array}{rcl}\overrightarrow{KP}=\dfrac{1}{3}\overrightarrow{KJ}&\Leftrightarrow&3\overrightarrow{KP}=\overrightarrow{KJ}\\\\&\Leftrightarrow&3\overrightarrow{KP}-\overrightarrow{KJ}=\vec{0}\\\\&\Leftrightarrow&3\overrightarrow{KP}-\overrightarrow{KP}-\overrightarrow{PJ}=\vec{0}\\\\&\Leftrightarrow&2\overrightarrow{KP}+\overrightarrow{JP}=\vec{0}\end{array}
 
D'où, \boxed{2\overrightarrow{KP}+\overrightarrow{JP}=\vec{0}}
 
Par conséquent, P est barycentre de (J\;;\ 1)\ et \ (K\;;\ 2).
 
Par ailleurs, d'après le résultat de la question 2\;), on a : C barycentre de (I\;;\ 4)\;,\ (J\;;\ 1)\ et \ (K\;;\ 2).
 
Donc, en appliquant la propriété d'associativité du barycentre, on obtient : C barycentre de (I\;;\ 4)\ et \ (P\;;\ 3).
 
D'où, les points I\;,\ C\;,\ P sont alignés.
 
Ce qui signifie que P appartient à la droite (CI), c'est-à-dire ; P\in(BC).
 
Ainsi, P\in(BC)\ et \ P\in(KJ)
 
D'où, \boxed{P\in(BC)\cap(KJ)}
 
Par conséquent, les droites (BC)\ et \ (KJ) sont sécantes en P.
 
Soit : \overrightarrow{IQ}=\dfrac{1}{3}\overrightarrow{IK}
 
Alors, Q appartient à la droite (KI) et on a :
 
\begin{array}{rcl}\overrightarrow{IQ}=\dfrac{1}{3}\overrightarrow{IK}&\Leftrightarrow&3\overrightarrow{IQ}=\overrightarrow{IK}\\\\&\Leftrightarrow&3\overrightarrow{IQ}-\overrightarrow{IK}=\vec{0}\\\\&\Leftrightarrow&3\overrightarrow{IQ}-\overrightarrow{IQ}-\overrightarrow{QK}=\vec{0}\\\\&\Leftrightarrow&2\overrightarrow{IQ}+\overrightarrow{KQ}=\vec{0}\end{array}
 
Donc, \boxed{2\overrightarrow{IQ}+\overrightarrow{KQ}=\vec{0}}
 
D'où, Q est barycentre de (I\;;\ 2)\ et \ (K\;;\ 1).
 
Par ailleurs, d'après le résultat de la question 2\;)\;,\ A est barycentre de (I\;;\ 2)\;,\ (J\;;\ 4)\ et \ (K\;;\ 1).
 
Donc, d'après la propriété d'associativité du barycentre, on a : A barycentre de (J\;;\ 4)\ et \ (Q\;;\ 3).
 
Par conséquent, les points A\;,\ J\;,\ Q sont alignés.
 
Ce qui signifie que Q appartient à la droite (AJ), ce qui peut encore s'écrire : Q\in(AC).
 
Donc, Q\in(AC)\ et \ Q\in(KI)
 
D'où, \boxed{P\in(AC)\cap(KI)}
 
Par suite, les droites (AC)\ et \ (KI) sont sécantes en Q.
 
Soit : \overrightarrow{JR}=\dfrac{1}{3}\overrightarrow{JI}
 
Alors, R\in(JI) et on a :
 
\begin{array}{rcl}\overrightarrow{JR}=\dfrac{1}{3}\overrightarrow{JI}&\Leftrightarrow&3\overrightarrow{JR}=\overrightarrow{JI}\\\\&\Leftrightarrow&3\overrightarrow{JR}-\overrightarrow{JI}=\vec{0}\\\\&\Leftrightarrow&3\overrightarrow{JR}-\overrightarrow{JR}-\overrightarrow{RI}=\vec{0}\\\\&\Leftrightarrow&2\overrightarrow{JR}+\overrightarrow{IR}=\vec{0}\end{array}
 
Ainsi, \boxed{2\overrightarrow{JR}+\overrightarrow{IR}=\vec{0}}
 
D'où, R est barycentre de (I\;;\ 1)\ et \ (J\;;\ 2).
 
Or, d'après le résultat de la question 2\;)\;,\ B est barycentre de (I\;;\ 1)\;,\ (J\;;\ 2)\ et \ (K\;;\ 4).
 
Donc, en appliquant la propriété d'associativité du barycentre, on obtient : B barycentre de (K\;;\ 4)\ et \ (R\;;\ 3).
 
Par conséquent, les points B\;,\ R\ et \ K sont alignés.
 
Par suite, R appartient à la droite (BK), c'est-à-dire ; R\in(AB).
 
Donc, R\in(AB)\ et \ R\in(JI)
 
D'où, \boxed{R\in(AB)\cap(JI)}
 
Ainsi, les droites (AB)\ et \ (JI) sont sécantes en R.

Exercice 16

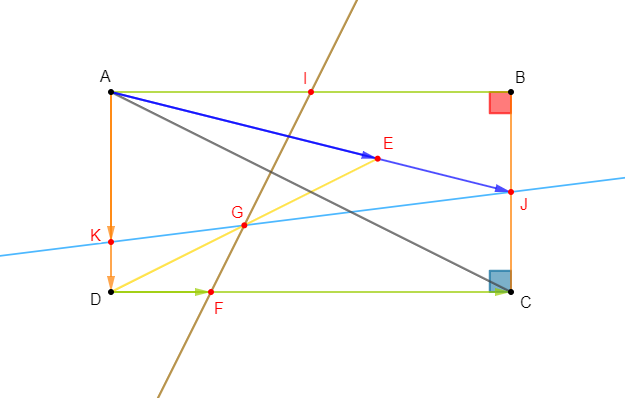
Soit ABC un triangle et k un réel non nul. Soient D\ et \ E définis par :
\overrightarrow{AD}=k\overrightarrow{AB}\ \text{ et }\ \overrightarrow{CE}=k\overrightarrow{CA}
1) Faisons une figure illustrant ces données pour k=\dfrac{1}{3}, puis pour k=-1.
 
Pour k=\dfrac{1}{3}, nous allons placer les points D\ et \ E tels que : 
\overrightarrow{AD}=\dfrac{1}{3}\overrightarrow{AB}\ \text{ et }\ \overrightarrow{CE}=\dfrac{1}{3}\overrightarrow{CA}
 

 
Pour k=-1, nous construisons les points D\ et \ E définis par : 
\overrightarrow{AD}=-\overrightarrow{AB}\ \text{ et }\ \overrightarrow{CE}=-\overrightarrow{CA}
 

 
2) Montrons que D est le barycentre de (A\;,\ 1-k)\ et \ (B\;,\ k)\ et \ E le barycentre de (C\;,\ 1-k)\ et \ (A\;,\ k).
 
En effet, soit la relation vectorielle suivante :
\overrightarrow{AD}=k\overrightarrow{AB}
Alors, en utilisant les propriétés du calcul vectoriel et en introduisant le point D dans le vecteur \overrightarrow{AB}, par la relation de Chasles, on obtient :
 
\begin{array}{rcl}\overrightarrow{AD}=k\overrightarrow{AB}&\Leftrightarrow&\overrightarrow{AD}-k\overrightarrow{AB}=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{AD}-k\left(\overrightarrow{AD}+\overrightarrow{DB}\right)=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{AD}-k\overrightarrow{AD}-k\overrightarrow{DB}=\vec{0}\\\\&\Leftrightarrow&(1-k)\overrightarrow{AD}+k\overrightarrow{BD}=\vec{0}\end{array}
 
Ainsi, \boxed{(1-k)\overrightarrow{AD}+k\overrightarrow{BD}=\vec{0}}
 
Ce qui montre que D est le barycentre de (A\;,\ 1-k)\ et \ (B\;,\ k).
 
De la même manière, considérons la relation vectorielle suivante :
\overrightarrow{CE}=k\overrightarrow{CA}
Alors, par la relation de Chasles, introduisons le point E dans le vecteur \overrightarrow{CA}.
 
On obtient :
 
\begin{array}{rcl}\overrightarrow{CE}=k\overrightarrow{CA}&\Leftrightarrow&\overrightarrow{CE}-k\overrightarrow{CA}=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{CE}-k\left(\overrightarrow{CE}+\overrightarrow{EA}\right)=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{CE}-k\overrightarrow{CE}-k\overrightarrow{EA}=\vec{0}\\\\&\Leftrightarrow&(1-k)\overrightarrow{CE}+k\overrightarrow{AE}=\vec{0}\end{array}
 
D'où, \boxed{(1-k)\overrightarrow{CE}+k\overrightarrow{AE}=\vec{0}}
 
Par conséquent, E est le barycentre de (C\;,\ 1-k)\ et \ (A\;,\ k).
 
3) En déduisons que, pour tout point M du plan, on a :
\overrightarrow{MD}+\overrightarrow{ME}=\overrightarrow{MA}+\overrightarrow{MC}+k\overrightarrow{CB}=2(\overrightarrow{MB'}+k\overrightarrow{B'C'})
où B'\ et \ C' sont les milieux respectifs de [AC]\ et \ [AB].
 
En effet, comme D est le barycentre de (A\;,\ 1-k)\ et \ (B\;,\ k) alors, d'après la propriété caractéristique, on a : pour tout point M du plan,
\overrightarrow{MD}=(1-k)\overrightarrow{MA}+k\overrightarrow{MB}
Aussi, comme E est le barycentre de (C\;,\ 1-k)\ et \ (A\;,\ k) alors, d'après la propriété caractéristique, on a : pour tout point M du plan,
\overrightarrow{ME}=(1-k)\overrightarrow{MC}+k\overrightarrow{MA}
Par suite, en remplaçant \overrightarrow{MD}\ et \ \overrightarrow{ME} par leur expression, on obtient :
 
\begin{array}{rcl}\overrightarrow{MD}+\overrightarrow{ME}&=&(1-k)\overrightarrow{MA}+k\overrightarrow{MB}+(1-k)\overrightarrow{MC}+k\overrightarrow{MA}\\\\&=&\overrightarrow{MA}-k\overrightarrow{MA}+k\overrightarrow{MB}+\overrightarrow{MC}-k\overrightarrow{MC}+k\overrightarrow{MA}\\\\&=&\overrightarrow{MA}+\overrightarrow{MC}+k\overrightarrow{CM}+k\overrightarrow{MB}\\\\&=&\overrightarrow{MA}+\overrightarrow{MC}+k\left(\overrightarrow{CM}+\overrightarrow{MB}\right)\\\\&=&\overrightarrow{MA}+\overrightarrow{MC}+k\overrightarrow{CB}\end{array}
 
D'où, \boxed{\overrightarrow{MD}+\overrightarrow{ME}=\overrightarrow{MA}+\overrightarrow{MC}+k\overrightarrow{CB}}
 
Par ailleurs, on sait que B'\ et \ C' sont les milieux respectifs de [AC]\ et \ [AB].
 
Donc, par la relation de Chasles, en introduisant le point A dans le vecteur \overrightarrow{CB} puis, respectivement les points B'\ et \ C', on obtient :
 
\begin{array}{rcl}\overrightarrow{MA}+\overrightarrow{MC}+k\overrightarrow{CB}&=&\overrightarrow{MA}+\overrightarrow{MC}+k\left(\overrightarrow{CA}+\overrightarrow{AB}\right)\\\\&=&\overrightarrow{MB'}+\overrightarrow{B'A}+\overrightarrow{MB'}+\overrightarrow{B'C}+k\left(\overrightarrow{CB'}+\overrightarrow{B'A}+\overrightarrow{AC'}+\overrightarrow{C'B}\right)\\\\&=&\overrightarrow{MB'}+\overrightarrow{MB'}+\underbrace{\overrightarrow{B'A}+\overrightarrow{B'C}}_{=\vec{0}}+k\left(2\overrightarrow{B'A}+2\overrightarrow{AC'}\right)\\\\&=&2\overrightarrow{MB'}+2k\left(\overrightarrow{B'A}+\overrightarrow{AC'}\right)\\\\&=&2\overrightarrow{MB'}+2k\overrightarrow{B'C'}\\\\&=&2\left(\overrightarrow{MB'}+k\overrightarrow{B'C'}\right)\end{array}
 
Ainsi, \boxed{\overrightarrow{MA}+\overrightarrow{MC}+k\overrightarrow{CB}=2\left(\overrightarrow{MB'}+k\overrightarrow{B'C'}\right)}
 
D'où, pour tout point M du plan, on a :
\boxed{\overrightarrow{MD}+\overrightarrow{ME}=\overrightarrow{MA}+\overrightarrow{MC}+k\overrightarrow{CB}=2\left(\overrightarrow{MB'}+k\overrightarrow{B'C'}\right)}
4) Montrons que [DE]\;,\ [AC]\ et \ [AB] ont leurs milieux alignés.
 
Soit H milieu de [DE].
 
Montrons alors que H\;,\ B'\ et \ C' sont alignés.
 
Comme H est le milieu de [DE] alors, en appliquant la propriété caractéristique, on obtient :
\overrightarrow{MD}+\overrightarrow{ME}=2\overrightarrow{MH}
Par suite, d'après le résultat de la question 3\;), on a :
 
\begin{array}{rcl}\overrightarrow{MD}+\overrightarrow{ME}=2(\overrightarrow{MB'}+k\overrightarrow{B'C'})&\Leftrightarrow&2\overrightarrow{MH}=2\left(\overrightarrow{MB'}+k\overrightarrow{B'C'}\right)\\\\&\Leftrightarrow&\overrightarrow{MH}=\overrightarrow{MB'}+k\overrightarrow{B'C'}\\\\&\Leftrightarrow&\overrightarrow{MH}-\overrightarrow{MB'}=k\overrightarrow{B'C'}\\\\&\Leftrightarrow&\overrightarrow{B'M}+\overrightarrow{MH}=k\overrightarrow{B'C'}\\\\&\Leftrightarrow&\overrightarrow{B'H}=k\overrightarrow{B'C'}\end{array}
 
D'où, \boxed{\overrightarrow{B'H}=k\overrightarrow{B'C'}}
 
Ce qui montre que les points H\;,\ B'\ et \ C' sont alignés.
 
Autrement dit, les segments [DE]\;,\ [AC]\ et \ [AB] ont leurs milieux alignés.

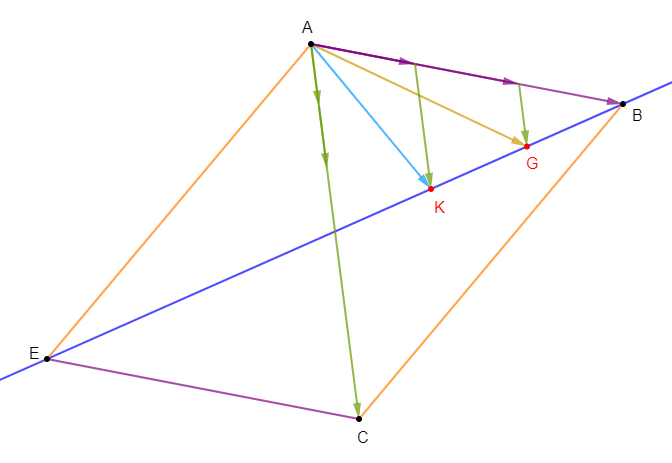
Exercice 17

Soient A\;,\ B\;,\ C trois points distincts ; a\;,\ b\;,\ c des réels tels que a+b+c\neq 0.
 
Soit G le barycentre des points pondérés (A\;,\ a)\;,\ (B\;,\ b)\ et \ (C\;,\ c).
 
1) Démontrons que les points pondérés (A\;,\ 2a+1)\;,\ (B\;,\ 2b-2)\ et \ (C\;,\ 2c+1) admettent un barycentre qu'on appellera K.
 
A\;,\ B\;,\ C étant trois points distincts alors, (A\;,\ 2a+1)\;,\ (B\;,\ 2b-2)\ et \ (C\;,\ 2c+1) admettent un barycentre si, et seulement si, la somme des coefficients de pondération est différente de zéro.
 
On a : 2a+1+2b-2+2c+1=2a+2b+2c=2(a+b+c)
 
Or, on sait que a+b+c\neq 0
 
Par suite, 2(a+b+c)\neq 0
 
D'où, les points pondérés (A\;,\ 2a+1)\;,\ (B\;,\ 2b-2)\ et \ (C\;,\ 2c+1) admettent un barycentre.
 
2) a) Donnons une relation vectorielle définissant K. et en déduisons que : a\overrightarrow{KA}+b\overrightarrow{KB}+c\overrightarrow{KC}=\dfrac{\overrightarrow{AB}+\overrightarrow{CB}}{2}
 
En effet, K barycentre de (A\;,\ 2a+1)\;,\ (B\;,\ 2b-2)\ et \ (C\;,\ 2c+1) alors, cela se traduit par la relation vectorielle suivante :
(2a+1)\overrightarrow{KA}+(2b-2)\overrightarrow{KB}+(2c+1)\overrightarrow{KC}=\vec{0}
En développant cette relation vectorielle, on obtient :
 
\begin{array}{rcl}(2a+1)\overrightarrow{KA}+(2b-2)\overrightarrow{KB}+(2c+1)\overrightarrow{KC}=\vec{0}&\Leftrightarrow&2a\overrightarrow{KA}+\overrightarrow{KA}+2b\overrightarrow{KB}-2\overrightarrow{KB}+2c\overrightarrow{KC}+\overrightarrow{KC}=\vec{0}\\\\&\Leftrightarrow&2a\overrightarrow{KA}+2b\overrightarrow{KB}+2c\overrightarrow{KC}+\overrightarrow{KA}-2\overrightarrow{KB}+\overrightarrow{KC}=\vec{0}\\\\&\Leftrightarrow&2\left(a\overrightarrow{KA}+b\overrightarrow{KB}+c\overrightarrow{KC}\right)+\overrightarrow{KA}-\overrightarrow{KB}-\overrightarrow{KB}+\overrightarrow{KC}=\vec{0}\\\\&\Leftrightarrow&2\left(a\overrightarrow{KA}+b\overrightarrow{KB}+c\overrightarrow{KC}\right)+\overrightarrow{BK}+\overrightarrow{KA}+\overrightarrow{BK}+\overrightarrow{KC}=\vec{0}\\\\&\Leftrightarrow&2\left(a\overrightarrow{KA}+b\overrightarrow{KB}+c\overrightarrow{KC}\right)+\overrightarrow{BA}+\overrightarrow{BC}=\vec{0}\\\\&\Leftrightarrow&2\left(a\overrightarrow{KA}+b\overrightarrow{KB}+c\overrightarrow{KC}\right)=-\overrightarrow{BA}-\overrightarrow{BC}\\\\&\Leftrightarrow&2\left(a\overrightarrow{KA}+b\overrightarrow{KB}+c\overrightarrow{KC}\right)=\overrightarrow{AB}+\overrightarrow{CB}\\\\&\Leftrightarrow&a\overrightarrow{KA}+b\overrightarrow{KB}+c\overrightarrow{KC}=\dfrac{\overrightarrow{AB}+\overrightarrow{CB}}{2}\end{array}
 
D'où, \boxed{a\overrightarrow{KA}+b\overrightarrow{KB}+c\overrightarrow{KC}=\dfrac{\overrightarrow{AB}+\overrightarrow{CB}}{2}}
 
b) En déduisons que G\ et \ K sont confondus si et seulement si B est le milieu du segment [AC].
 
On a : G\ et \ K confondus alors, 
a\overrightarrow{GA}+b\overrightarrow{GB}+c\overrightarrow{GC}=a\overrightarrow{KA}+b\overrightarrow{KB}+c\overrightarrow{KC}
Ainsi, d'après le résultat de la question 2\;)\;a\;), on a :
 
\begin{array}{rcl}a\overrightarrow{GA}+b\overrightarrow{GB}+c\overrightarrow{GC}=a\overrightarrow{KA}+b\overrightarrow{KB}+c\overrightarrow{KC}&\Leftrightarrow&\dfrac{\overrightarrow{AB}+\overrightarrow{CB}}{2}=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{AB}+\overrightarrow{CB}=\vec{0}\end{array}
 
Ainsi, \boxed{\overrightarrow{AB}+\overrightarrow{CB}=\vec{0}}
 
Ce qui signifie que B est le milieu de [AC].
 
3) On suppose que A\;,\ B\ et \ C ne sont pas alignés. Soit E le point vérifiant que ABCE est un parallélogramme.
 
Démontrons que :
\overrightarrow{GK}=\dfrac{\overrightarrow{BE}}{2(a+b+c)}
D'après le résultat de la question 2\;), on a :
a\overrightarrow{KA}+b\overrightarrow{KB}+c\overrightarrow{KC}=\dfrac{\overrightarrow{AB}+\overrightarrow{CB}}{2}
Or, on sait que ABCE est un parallélogramme.
 
Donc, \overrightarrow{AB}=\overrightarrow{EC}
 
Ainsi, par la relation de Chasles, en introduisant G dans les vecteurs \overrightarrow{KA}\;,\ \overrightarrow{KB}\ et \ \overrightarrow{KC} puis, en remplaçant \overrightarrow{AB} par \overrightarrow{EC}, on obtient :
 
\begin{array}{rcl}a\overrightarrow{KA}+b\overrightarrow{KB}+c\overrightarrow{KC}=\dfrac{\overrightarrow{AB}+\overrightarrow{CB}}{2}&\Leftrightarrow&a\left(\overrightarrow{KG}+\overrightarrow{GA}\right)+b\left(\overrightarrow{KG}+\overrightarrow{GB}\right)+c\left(\overrightarrow{KG}+\overrightarrow{GC}\right)=\dfrac{\overrightarrow{EC}+\overrightarrow{CB}}{2}\\\\&\Leftrightarrow&a\overrightarrow{KG}+a\overrightarrow{GA}+b\overrightarrow{KG}+b\overrightarrow{GB}+c\overrightarrow{KG}+c\overrightarrow{GC}=\dfrac{\overrightarrow{EB}}{2}\\\\&\Leftrightarrow&(a+b+c)\overrightarrow{KG}+\underbrace{a\overrightarrow{GA}+b\overrightarrow{GB}+c\overrightarrow{GC}}_{=\vec{0}}=\dfrac{\overrightarrow{EB}}{2}\\\\&\Leftrightarrow&\overrightarrow{KG}=\dfrac{\overrightarrow{EB}}{2(a+b+c)}\\\\&\Leftrightarrow&\overrightarrow{GK}=\dfrac{\overrightarrow{BE}}{2(a+b+c)}\end{array}
 
D'où, \boxed{\overrightarrow{GK}=\dfrac{\overrightarrow{BE}}{2(a+b+c)}}
 
On pose a=c=\dfrac{1}{2} et b=2. Construisons les points G\ et \ K.
 
D'après la propriété caractéristique, on a :
 
\begin{array}{rcl}\overrightarrow{AG}&=&\dfrac{2\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}}{3}\\\\&=&\dfrac{2}{3}\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AC}\end{array}
 
\begin{array}{rcl}\overrightarrow{AK}&=&\dfrac{2\overrightarrow{AB}+2\overrightarrow{AC}}{6}\\\\&=&\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\end{array}
 
Pour le point K, on peut aussi appliquer le résultat de la question 3\;).
 
On a alors : \overrightarrow{GK}=\dfrac{\overrightarrow{BE}}{6}

 

Exercice 18

Soit ABC un triangle équilatéral de côté a=4\;cm.
 
Soit D le point défini par :
3\overrightarrow{DA}-\overrightarrow{AB}+2\overrightarrow{AC}=\vec{0}
1) Exprimons D comme barycentre de A\;,\ B\ et \ C affectés de coefficients à préciser.
 
Soit : 3\overrightarrow{DA}-\overrightarrow{AB}+2\overrightarrow{AC}=\vec{0}
 
Alors, par la relation de Chasles, introduisons le point D dans les vecteurs \overrightarrow{AB}\ et \ \overrightarrow{AC}.
 
On obtient :
 
\begin{array}{rcl}3\overrightarrow{DA}-\overrightarrow{AB}+2\overrightarrow{AC}=\vec{0}&\Leftrightarrow&3\overrightarrow{DA}-\left(\overrightarrow{AD}+\overrightarrow{DB}\right)+2\left(\overrightarrow{AD}+\overrightarrow{DC}\right)=\vec{0}\\\\&\Leftrightarrow&3\overrightarrow{DA}-\overrightarrow{AD}-\overrightarrow{DB}+2\overrightarrow{AD}+2\overrightarrow{DC}=\vec{0}\\\\&\Leftrightarrow&3\overrightarrow{DA}+\overrightarrow{DA}-2\overrightarrow{DA}-\overrightarrow{DB}+2\overrightarrow{DC}=\vec{0}\\\\&\Leftrightarrow&2\overrightarrow{DA}-\overrightarrow{DB}+2\overrightarrow{DC}=\vec{0}\end{array}
 
Donc, \boxed{2\overrightarrow{DA}-\overrightarrow{DB}+2\overrightarrow{DC}=\vec{0}\qquad(1)}
 
Par conséquent, D est le barycentre du système
\{(A\;,\ 2)\;;\ (B\;,\ -1)\;;\ (C\;,\ 2)\}
2) Soit I le milieu de [AC]. Montrons que D est barycentre de B\ et \ I affectés de coefficients à préciser.
 
En effet, comme I est le milieu de [AC] alors,
\overrightarrow{IA}+\overrightarrow{IB}=\vec{0}
Ainsi, dans la relation (1) de la question 1\;), introduisons, par la relation de Chasles, le point I dans les vecteurs \overrightarrow{DA}\ et \ \overrightarrow{DC}.
 
On obtient alors :
 
\begin{array}{rcl}2\overrightarrow{DA}-\overrightarrow{DB}+2\overrightarrow{DC}=\vec{0}&\Leftrightarrow&2\left(\overrightarrow{DI}+\overrightarrow{IA}\right)-\overrightarrow{DB}+2\left(\overrightarrow{DI}+\overrightarrow{CC}\right)=\vec{0}\\\\&\Leftrightarrow&2\overrightarrow{DI}+2\overrightarrow{IA}-\overrightarrow{DB}+2\overrightarrow{DI}+2\overrightarrow{IC}=\vec{0}\\\\&\Leftrightarrow&2\overrightarrow{DI}+2\overrightarrow{DI}-\overrightarrow{DB}+2\overrightarrow{IA}+2\overrightarrow{IC}=\vec{0}\\\\&\Leftrightarrow&4\overrightarrow{DI}-\overrightarrow{DB}+2\left(\underbrace{\overrightarrow{IA}+\overrightarrow{IC}}_{=\vec{0}}\right)=\vec{0}\\\\&\Leftrightarrow&4\overrightarrow{DI}-\overrightarrow{DB}=\vec{0}\end{array}
 
D'où, \boxed{4\overrightarrow{DI}-\overrightarrow{DB}=\vec{0}\qquad(2)}
 
Ce qui montre que D est le barycentre du système
\{(B\;,\ -1)\;;\ (I\;,\ 4)\}
Autre méthode
 
Soit D barycentre de (A\;,\ 2)\;;\ (B\;,\ -1)\ et \ (C\;,\ 2).
 
Or, I est le milieu de [AC].
 
Donc, I est barycentre de (A\;,\ 2)\ et \ (C\;,\ 2).
 
Ainsi, en appliquant la propriété d'associativité du barycentre, D est le barycentre du système
\{(B\;,\ -1)\;;\ (I\;,\ 4)\}
En déduisons que D est le symétrique de G par rapport à I\ (G étant le centre de gravité du triangle ABC)
 
En effet, comme I est milieu de [AC] alors, [BI] est une médiane du triangle ABC.
 
Or, on sait que le centre de gravité G de ce triangle se situe au tiers de cette médiane en partant de I. Ce qui peut encore s'écrire :
\overrightarrow{IG}=\dfrac{1}{3}\overrightarrow{IB}\qquad(3)
Par ailleurs, comme D est barycentre de (B\;,\ -1)\ et \ (I\;,\ 4) alors, par la relation de Chasles, en introduisant le point I dans le vecteur \overrightarrow{DB} de la relation (2), on obtient :
 
\begin{array}{rcl}4\overrightarrow{DI}-\overrightarrow{DB}=\vec{0}&\Leftrightarrow&4\overrightarrow{DI}-\left(\overrightarrow{DI}+\overrightarrow{IB}\right)=\vec{0}\\\\&\Leftrightarrow&4\overrightarrow{DI}-\overrightarrow{DI}-\overrightarrow{IB}=\vec{0}\\\\&\Leftrightarrow&3\overrightarrow{DI}-\overrightarrow{IB}=\vec{0}\\\\&\Leftrightarrow&3\overrightarrow{DI}=\overrightarrow{IB}\\\\&\Leftrightarrow&\overrightarrow{DI}=\dfrac{\overrightarrow{IB}}{3}\end{array}
 
Donc, on a :
\overrightarrow{DI}=\dfrac{1}{3}\overrightarrow{IB}\qquad(4)
Ainsi, en regroupant les relations (3)\ et \ (4), on peut écrire :
\left\lbrace\begin{array}{rcl}\overrightarrow{IG}&=&\dfrac{1}{3}\overrightarrow{IB}\\\\\overrightarrow{DI}&=&\dfrac{1}{3}\overrightarrow{IB}\end{array}\right.
Par comparaison, on trouve :
\overrightarrow{DI}=\overrightarrow{IG}
Ce qui signifie que I est le milieu de [DG].
 
Par conséquent, D\ et \ G sont symétriques par rapport à I.
 
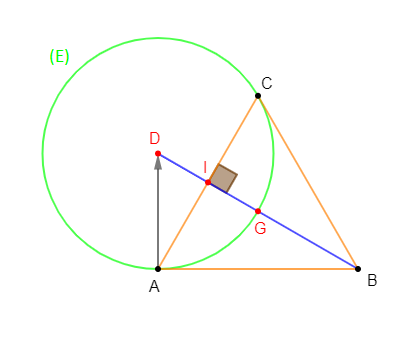
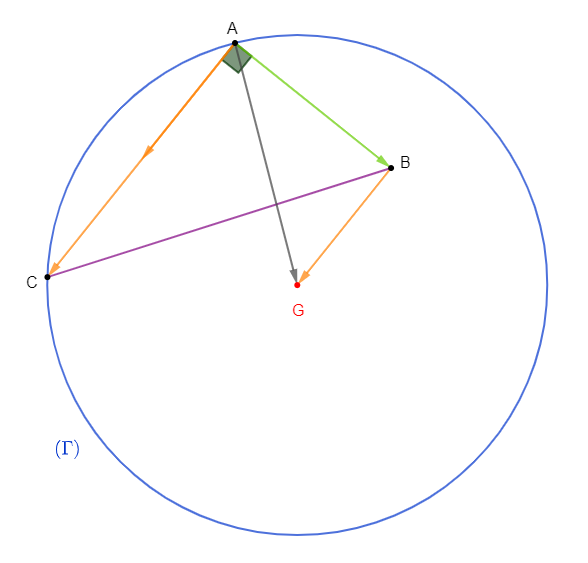
3) Soit (E) l'ensemble des points M du plan tels que :
\|2\overrightarrow{MA}-\overrightarrow{MB}+2\overrightarrow{MC}\|=4\sqrt{3}\qquad(5)
Déterminons (E).
 
En effet, comme D est le barycentre de (A\;;\ 2)\;,\ (B\;;\ -1)\;,\ (C\;;\ 2) alors, d'après la propriété caractéristique, on a :
2\overrightarrow{MA}-\overrightarrow{MB}+2\overrightarrow{MC}=3\overrightarrow{MD}
Ainsi, dans la relation (5), en remplaçant 2\overrightarrow{MA}-\overrightarrow{MB}+2\overrightarrow{MC} par 3\overrightarrow{MD}, on obtient :
 
\begin{array}{rcl}\|2\overrightarrow{MA}-\overrightarrow{MB}+2\overrightarrow{MC}\|=4\sqrt{3}&\Leftrightarrow&\|3\overrightarrow{MD}\|=4\sqrt{3}\\ \\ &\Leftrightarrow&3\|\overrightarrow{MD}\|=4\sqrt{3}\\\\&\Leftrightarrow&\|\overrightarrow{MD}\|=\dfrac{4\sqrt{3}}{3}\end{array}
 
D'où, \boxed{\|\overrightarrow{MD}\|=\dfrac{4\sqrt{3}}{3}}
 
Ce qui est caractéristique d'un cercle de centre D et de rayon \dfrac{4\sqrt{3}}{3}.
 
Donc, \boxed{(E)=\mathcal{C}\left(D\;,\ \dfrac{4\sqrt{3}}{3}\right)}
 
Vérifions que G appartient à (E) et construisons (E).
 
En effet, G appartient à (E) si, et seulement si,
GD=4\sqrt{3}
Calculons alors la longueur GD.
 
D étant le symétrique de G par rapport à I alors,
GD=2IG
Or, IG=\dfrac{1}{3}IB
 
Par suite,
GD=\dfrac{2}{3}IB\qquad(6)
Par ailleurs, comme le triangle BIC est rectangle en I alors, d'après le théorème de Pythagore, on a :
IB^{2}+IC^{2}=BC^{2}
Donc,
 
\begin{array}{rcl}IB^{2}+IC^{2}=BC^{2}&\Rightarrow&IB^{2}=BC^{2}-IC^{2}\\\\&\Rightarrow&IB=\sqrt{BC^{2}-IC^{2}}\\\\&\Rightarrow&IB=\sqrt{4^{2}-2^{2}}\\\\&\Rightarrow&IB=\sqrt{16-4}\\\\&\Rightarrow&IB=\sqrt{12}\\\\&\Rightarrow&IB=2\sqrt{3}\end{array}
 
Ainsi, en remplaçant IB par sa valeur, dans la relation (6), on obtient :
GD=\dfrac{2}{3}IB=\dfrac{2\times 2\sqrt{3}}{3}=\dfrac{4\sqrt{3}}{3}
D'où, \boxed{GD=\dfrac{4\sqrt{3}}{3}}
 
Ce qui prouve que G appartient à (E).
 
Enfin, pour construire (E), on place G et on trace le cercle de centre D et passant par G.

 
 

Exercice 19

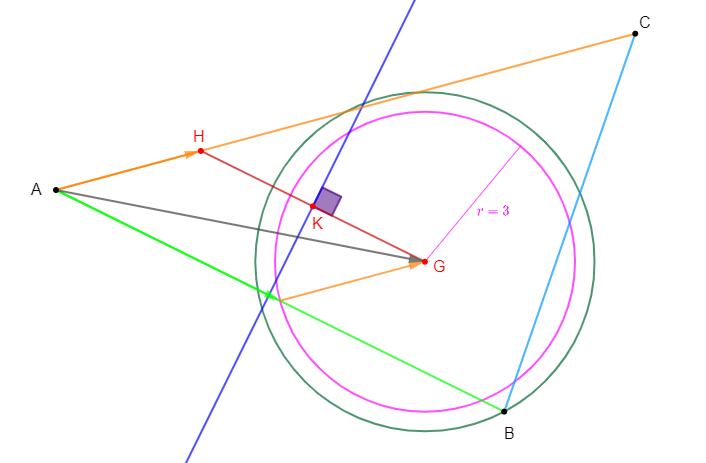
1) Construisons un triangle ABC tel que :
AC=12\;,\ BA=10\quad\text{ et }\quad CB=8
Soit G barycentre de (A\;,\ 1)\;,\ (B\;,\ 2)\ et \ (C\;,\ 1).
 
Alors, d'après la propriété caractéristique, on a :
 
\begin{array}{rcl}\overrightarrow{AG}&=&\dfrac{2\overrightarrow{AB}+\overrightarrow{AC}}{4}\\\\&=&\dfrac{2}{4}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\\\\&=&\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\end{array}
 
Donc, plaçons G tel que :
\overrightarrow{AG}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}
2) Déterminons et représentons l'ensemble des points M du plan tels que :
\|\overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC}\|=AC\qquad(1)
G étant le barycentre de (A\;;\ 1)\;,\ (B\;;\ 2)\;,\ (C\;;\ 1) alors, d'après la propriété caractéristique, on a :
\overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC}=4\overrightarrow{MG}
Ainsi, dans la relation (1), en remplaçant \overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC} par 4\overrightarrow{MG}, on obtient :
 
\begin{array}{rcl}\|\overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC}\|=AC&\Leftrightarrow&\|4\overrightarrow{MG}\|=12\\ \\ &\Leftrightarrow&4\|\overrightarrow{MG}\|=12\\\\&\Leftrightarrow&\|\overrightarrow{MG}\|=\dfrac{12}{4}\\\\&\Leftrightarrow&\|\overrightarrow{MG}\|=3\end{array}
 
D'où, \boxed{\|\overrightarrow{MG}\|=3}
 
Ce qui représente un cercle de centre G et de rayon 3.
 
Donc, l'ensemble des points M du plan tels que \|\overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC}\|=AC est le cercle de centre G et de rayon 3.
 
3) Soit (E) l'ensemble des points M du plan tels que :
\|\overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC}\|=\|\overrightarrow{BA}+\overrightarrow{BC}\|\qquad(2)
Montrons que B appartient à (E).
 
B appartient à (E) si, et seulement si, B vérifie la relation (2).
 
Soit la relation suivante :
\|\overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC}\|
Alors, en remplaçant M par B, on obtient :
\|\overrightarrow{BA}+2\overrightarrow{BB}+\overrightarrow{BC}\|=\|\overrightarrow{BA}+\overrightarrow{BC}\|
Donc, B vérifie bien la relation (2).
 
Par conséquent, B appartient à (E).
 
Déterminons et représentons l'ensemble (E).
 
Comme G est le barycentre de (A\;;\ 1)\;,\ (B\;;\ 2)\;,\ (C\;;\ 1) alors, d'après la propriété caractéristique, on a :
\overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC}=4\overrightarrow{MG}
Ainsi, dans la relation (2), en remplaçant \overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC} par 4\overrightarrow{MG}, on obtient :
 
\begin{array}{rcl}\|\overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC}\|=\|\overrightarrow{BA}+\overrightarrow{BC}\|&\Leftrightarrow&\|4\overrightarrow{MG}\|=\|\overrightarrow{BA}+\overrightarrow{BC}\|\\ \\ &\Leftrightarrow&4\|\overrightarrow{MG}\|=\|\overrightarrow{BA}+\overrightarrow{BC}\|\\\\&\Leftrightarrow&\|\overrightarrow{MG}\|=\dfrac{\|\overrightarrow{BA}+\overrightarrow{BC}\|}{4}\end{array}
 
Donc, \boxed{\|\overrightarrow{MG}\|=\dfrac{\|\overrightarrow{BA}+\overrightarrow{BC}\|}{4}}
 
On obtient alors un cercle de centre G et de rayon \dfrac{\|\overrightarrow{BA}+\overrightarrow{BC}\|}{4}.
 
Ainsi, l'ensemble (E) est le cercle de centre G et de rayon \dfrac{\|\overrightarrow{BA}+\overrightarrow{BC}\|}{4}.
 
Comme B est un élément de (E) alors, pour représenter (E) il suffit de tracer le cercle de centre G et passant par la pont B.
 
4) Déterminons et représentons l'ensemble des points M du plan tels que :
\|\overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC}\|=\|3\overrightarrow{MA}+\overrightarrow{MC}\|\qquad(3)
Considérons H barycentre de (A\;;\ 3)\ et \ (C\;;\ 1).
 
Alors, d'après la propriété caractéristique, on a :
3\overrightarrow{MA}+\overrightarrow{MC}=4\overrightarrow{MH}
Par ailleurs, comme G est le barycentre de (A\;;\ 1)\;,\ (B\;;\ 2)\;,\ (C\;;\ 1) alors, d'après la propriété caractéristique, on obtient :
\overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC}=4\overrightarrow{MG}
Ainsi, dans la relation (3), en remplaçant \overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC} par 4\overrightarrow{MG}\ et \ 3\overrightarrow{MA}+\overrightarrow{MC} par 4\overrightarrow{MH}, on obtient :
 
\begin{array}{rcl} \|\overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC}\|=\|3\overrightarrow{MA}+\overrightarrow{MC}\|&\Leftrightarrow&\|4\overrightarrow{MG}\|=\|4\overrightarrow{MH}\|\\ \\ &\Leftrightarrow&\|\overrightarrow{MG}\|=\|\overrightarrow{MH}\|\end{array}
 
Donc, \boxed{\|\overrightarrow{MG}\|=\|\overrightarrow{MH}\|}
 
On reconnait alors la médiatrice du segment [GH]
 
D'où, l'ensemble des points M du plan tels que \|\overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC}\|=\|3\overrightarrow{MA}+\overrightarrow{MC}\| est la médiatrice du segment [GH].
 
C'est la droite perpendiculaire à (GH) et passant par le milieu K du segment [GH].

 

Exercice 20

On considère trois points A\;,\ B\;,\ C non alignés affectés des coefficients respectifs 1\;,\ 2\ et \ -3.
 
1) Ces points pondérés n'admettent pas de barycentre.
 
En effet, les trois points A\;,\ B\;,\ C non alignés admettent un barycentre si, et seulement si, la somme de leur coefficient de pondération est non nulle.
 
Or, on a :
1+2-3=0
Par conséquent, les points A\;,\ B\ et \ C n'ont pas de barycentre.
 
2) Montrons que lorsque M se déplace dans le plan, le vecteur \overrightarrow{MA}+2\overrightarrow{MB}-3\overrightarrow{MC} reste constant.
 
Par la relation de Chasles, introduisons le point A dans les vecteurs \overrightarrow{MB}\ et \ \overrightarrow{MC}.
 
On obtient alors :
 
\begin{array}{rcl}\overrightarrow{MA}+2\overrightarrow{MB}-3\overrightarrow{MC}&=&\overrightarrow{MA}+2\left(\overrightarrow{MA}+\overrightarrow{AB}\right)-3\left(\overrightarrow{MA}+\overrightarrow{AC}\right)\\\\&=&\overrightarrow{MA}+2\overrightarrow{MA}+2\overrightarrow{AB}-3\overrightarrow{MA}-3\overrightarrow{AC}\\\\&=&\overrightarrow{MA}+2\overrightarrow{MA}-3\overrightarrow{MA}+2\overrightarrow{AB}-3\overrightarrow{AC}\\\\&=&2\overrightarrow{AB}-3\overrightarrow{AC}\end{array}
 
D'où, \boxed{\overrightarrow{MA}+2\overrightarrow{MB}-3\overrightarrow{MC}=2\overrightarrow{AB}-3\overrightarrow{AC}}
 
On constate que la somme vectorielle 2\overrightarrow{AB}-3\overrightarrow{AC} ne dépend pas du point M et reste toujours constante.
 
Par conséquent, lorsque M se déplace dans le plan, le vecteur \overrightarrow{MA}+2\overrightarrow{MB}-3\overrightarrow{MC} reste constant.
 
On note \vec{u} ce vecteur constant. Construisons le point D tel que :
\overrightarrow{AD}=\vec{u}
On a : \vec{u}=2\overrightarrow{AB}-3\overrightarrow{AC}
 
Donc, \overrightarrow{AD}=\vec{u}\ \Leftrightarrow\ \overrightarrow{AD}=2\overrightarrow{AB}-3\overrightarrow{AC}
 
Donc, plaçons le point D tel que :
\overrightarrow{AD}=2\overrightarrow{AB}-3\overrightarrow{AC}
3) Construction de barycentres
 
Soit A' barycentre de (B\;,\ 2)\ et \ (C\;,\ -3) alors, d'après la propriété caractéristique, on a :
\overrightarrow{BA'}=3\overrightarrow{BC} 
Soit B' barycentre de (C\;,\ -3)\ et \ (A\;,\ 1) alors, en appliquant la propriété caractéristique, on obtient :
\overrightarrow{AB'}=\dfrac{3}{2}\overrightarrow{AC}
Soit C' barycentre de (A\;,\ 1)\ et \ (B\;,\ 2) alors, d'après la propriété caractéristique, on a :
\overrightarrow{AC'}=\dfrac{2}{3}\overrightarrow{AB}
Ainsi, plaçons les points A'\;,\ B'\ et \ C' tels que :
\overrightarrow{BA'}=3\overrightarrow{BC}\;,\quad \overrightarrow{AB'}=\dfrac{3}{2}\overrightarrow{AC}\;,\quad \overrightarrow{AC'}=\dfrac{2}{3}\overrightarrow{AB}
Démontrons que :
\vec{u}=-\overrightarrow{AA'}=-2\overrightarrow{BB'}=3\overrightarrow{CC'}
D'après le résultat de la question 2\;), on a :
\vec{u}=2\overrightarrow{AB}-3\overrightarrow{AC}
Alors, par la relation de Chasles, introduisons le point A' dans les vecteurs \overrightarrow{AB}\ et \ \overrightarrow{AC}.
 
Ainsi, on a :
 
\begin{array}{rcl}\vec{u}&=&2\overrightarrow{AB}-3\overrightarrow{AC}\\\\&=&2\left(\overrightarrow{AA'}+\overrightarrow{A'B}\right)-3\left(\overrightarrow{AA'}+\overrightarrow{A'C}\right)\\\\&=&2\overrightarrow{AA'}+2\overrightarrow{A'B}-3\overrightarrow{AA'}-3\overrightarrow{A'C}\\\\&=&2\overrightarrow{AA'}-3\overrightarrow{AA'}+\underbrace{2\overrightarrow{A'B}-3\overrightarrow{A'C}}_{=\vec{0}}\\\\&=&-\overrightarrow{AA'}\end{array}
 
D'où, \boxed{\vec{u}=-\overrightarrow{AA'}}
 
Encore, par la relation de Chasles, en introduisant le point B' dans les vecteurs \overrightarrow{AB}\ et \ \overrightarrow{AC}, on obtient :
 
\begin{array}{rcl}\vec{u}&=&2\overrightarrow{AB}-3\overrightarrow{AC}\\\\&=&2\left(\overrightarrow{AB'}+\overrightarrow{B'B}\right)-3\left(\overrightarrow{AB'}+\overrightarrow{B'C}\right)\\\\&=&2\overrightarrow{AB'}+2\overrightarrow{B'B}-3\overrightarrow{AB'}-3\overrightarrow{B'C}\\\\&=&2\overrightarrow{AB'}-3\overrightarrow{AB'}-3\overrightarrow{B'C}+2\overrightarrow{B'B}\\\\&=&-\overrightarrow{AB'}-3\overrightarrow{B'C}+2\overrightarrow{B'B}\\\\&=&\underbrace{\overrightarrow{B'A}-3\overrightarrow{B'C}}_{=\vec{0}}-2\overrightarrow{BB'}\end{array}
 
Ainsi, \boxed{\vec{u}=-2\overrightarrow{BB'}}
 
Par ailleurs, d'après la relation de Chasles, introduisons le point C' dans les vecteurs \overrightarrow{AB}\ et \ \overrightarrow{AC}.
 
On obtient alors :
 
\begin{array}{rcl}\vec{u}&=&2\overrightarrow{AB}-3\overrightarrow{AC}\\\\&=&2\left(\overrightarrow{AC'}+\overrightarrow{C'B}\right)-3\left(\overrightarrow{AC'}+\overrightarrow{C'C}\right)\\\\&=&2\overrightarrow{AC'}+2\overrightarrow{C'B}-3\overrightarrow{AC'}-3\overrightarrow{C'C}\\\\&=&2\overrightarrow{AC'}-3\overrightarrow{AC'}+2\overrightarrow{C'B}-3\overrightarrow{C'C}\\\\&=&-\overrightarrow{AC'}+2\overrightarrow{C'B}-3\overrightarrow{C'C}\\\\&=&\underbrace{\overrightarrow{C'A}+2\overrightarrow{C'B}}_{=\vec{0}}+3\overrightarrow{CC'}\\\\&=&3\overrightarrow{CC'}\end{array}
 
Donc, \boxed{\vec{u}=3\overrightarrow{CC'}}
 
Ainsi, on a :
\left\lbrace\begin{array}{rcl}\vec{u}&=&-\overrightarrow{AA'}\\\\\vec{u}&=&-2\overrightarrow{BB'}\\\\\vec{u}&=&3\overrightarrow{CC'}\end{array}\right.
D'où, \boxed{\vec{u}=-\overrightarrow{AA'}=-2\overrightarrow{BB'}=3\overrightarrow{CC'}}
 
Alors, on peut en déduire que les droites (AA')\;,\ (BB')\ et \ (CC') sont parallèles.
 
En effet, d'après le résultat précédent, on peut écrire :
-\overrightarrow{AA'}=-2\overrightarrow{BB'}=3\overrightarrow{CC'}
Ce qui signifie que les vecteurs -\overrightarrow{AA'}\;,\ -2\overrightarrow{BB'}\;,\ et \ 3\overrightarrow{CC'} sont colinéaires.
 
Par conséquent, les droites (AA')\;,\ (BB')\ et \ (CC') sont parallèles.

 
 
 

Exercice 22

On se donne un triangle ABC. Pour tout point M du plan , on pose :
\overrightarrow{f(M)}=2\overrightarrow{MA}-3\overrightarrow{MB}+\overrightarrow{MC}
1) P désignant un point quelconque du plan , prouvons que \overrightarrow{f(M)}=\overrightarrow{f(P)}.
 
Cela revient donc à montrer que f est constante.
 
En d'autres termes ; \overrightarrow{f(M)} est ne dépend pas de M.
 
Soit : \overrightarrow{f(M)}=2\overrightarrow{MA}-3\overrightarrow{MB}+\overrightarrow{MC} alors, par la relation de Chasles, introduisons le point B dans les vecteurs \overrightarrow{MA}\ et \ \overrightarrow{MC}.
 
On obtient :
 
\begin{array}{rcl}\overrightarrow{f(M)}&=&2\overrightarrow{MA}-3\overrightarrow{MB}+\overrightarrow{MC}\\\\&=&2\left(\overrightarrow{MB}+\overrightarrow{BA}\right)-3\overrightarrow{MB}+\left(\overrightarrow{MB}+\overrightarrow{BC}\right)\\\\&=&2\overrightarrow{MB}+2\overrightarrow{BA}-3\overrightarrow{MB}+\overrightarrow{MB}+\overrightarrow{BC}\\\\&=&2\overrightarrow{MB}+\overrightarrow{MB}-3\overrightarrow{MB}+2\overrightarrow{BA}+\overrightarrow{BC}\\\\&=&2\overrightarrow{BA}+\overrightarrow{BC}\end{array}
 
D'où, \boxed{\overrightarrow{f(M)}=2\overrightarrow{BA}+\overrightarrow{BC}}
 
On remarque que la somme vectorielle 2\overrightarrow{BA}+\overrightarrow{BC} ne dépend pas du point M.
 
Ce qui montre que f est constante.
 
2) Construisons G_{1} barycentre (B\;;\ -3)\ et \ (C\;;\ 1).
 
D'après la propriété caractéristique, on a :
\overrightarrow{BG_{1}}=-\dfrac{1}{2}\overrightarrow{BC}
Montrons que \overrightarrow{f(M)}=2\overrightarrow{G_{1}A}
 
D'après le résultat de la question 1\;), on a :
\overrightarrow{f(M)}=2\overrightarrow{BA}+\overrightarrow{BC}
Donc, par la relation de Chasles, en introduisant le point G_{1} dans les vecteurs \overrightarrow{BA}\ et \ \overrightarrow{BC}, on obtient :
 
\begin{array}{rcl}\overrightarrow{f(M)}&=&2\overrightarrow{BA}+\overrightarrow{BC}\\\\&=&2\left(\overrightarrow{BG_{1}}+\overrightarrow{G_{1}A}\right)+\left(\overrightarrow{BG_{1}}+\overrightarrow{G_{1}C}\right)\\\\&=&2\overrightarrow{BG_{1}}+2\overrightarrow{G_{1}A}+\overrightarrow{BG_{1}}+\overrightarrow{G_{1}C}\\\\&=&2\overrightarrow{BG_{1}}+\overrightarrow{BG_{1}}+\overrightarrow{G_{1}C}+2\overrightarrow{G_{1}A}\\\\&=&3\overrightarrow{BG_{1}}+\overrightarrow{G_{1}C}+2\overrightarrow{G_{1}A}\\\\&=&\underbrace{-3\overrightarrow{G_{1}B}+\overrightarrow{G_{1}C}}_{=\vec{0}}+2\overrightarrow{G_{1}A}\\\\&=&2\overrightarrow{G_{1}A}\end{array}
 
D'où, \boxed{\overrightarrow{f(M)}=2\overrightarrow{G_{1}A}}
 
3) Construisons G_{2} barycentre (A\;;\ 2)\ et \ (C\;;\ 1).
 
En appliquant la propriété caractéristique, on obtient :
\overrightarrow{AG_{2}}=\dfrac{1}{3}\overrightarrow{AC}
Montrons que \overrightarrow{f(M)}=3\overrightarrow{BG}_{2}
 
Soit : \overrightarrow{f(M)}=2\overrightarrow{BA}+\overrightarrow{BC}
 
Alors, par la relation de Chasles, en introduisant le point G_{2} dans les vecteurs \overrightarrow{BA}\ et \ \overrightarrow{BC}, on obtient :
 
\begin{array}{rcl}\overrightarrow{f(M)}&=&2\overrightarrow{BA}+\overrightarrow{BC}\\\\&=&2\left(\overrightarrow{BG_{2}}+\overrightarrow{G_{2}A}\right)+\left(\overrightarrow{BG_{2}}+\overrightarrow{G_{2}C}\right)\\\\&=&2\overrightarrow{BG_{2}}+2\overrightarrow{G_{2}A}+\overrightarrow{BG_{2}}+\overrightarrow{G_{2}C}\\\\&=&2\overrightarrow{BG_{2}}+\overrightarrow{BG_{2}}+2\overrightarrow{G_{2}A}+\overrightarrow{G_{2}C}\\\\&=&3\overrightarrow{BG_{2}}+\underbrace{2\overrightarrow{G_{2}A}+\overrightarrow{G_{2}C}}_{=\vec{0}}\\\\&=&3\overrightarrow{BG_{2}}\end{array}
 
Donc, \boxed{\overrightarrow{f(M)}=3\overrightarrow{BG_{2}}}
 
4) On désigne par G_{3} le barycentre de (B\;;\ -3)\ et \ (A\;;\ 2).
 
Alors, de la même manière, introduisons le point G_{2} dans les vecteurs \overrightarrow{BA}\ et \ \overrightarrow{BC}.
 
On obtient :
 
\begin{array}{rcl}\overrightarrow{f(M)}&=&2\overrightarrow{BA}+\overrightarrow{BC}\\\\&=&2\left(\overrightarrow{BG_{3}}+\overrightarrow{G_{3}A}\right)+\left(\overrightarrow{BG_{3}}+\overrightarrow{G_{3}C}\right)\\\\&=&2\overrightarrow{BG_{3}}+2\overrightarrow{G_{3}A}+\overrightarrow{BG_{3}}+\overrightarrow{G_{3}C}\\\\&=&2\overrightarrow{BG_{3}}+\overrightarrow{BG_{3}}+2\overrightarrow{G_{3}A}+\overrightarrow{G_{3}C}\\\\&=&3\overrightarrow{BG_{3}}+2\overrightarrow{G_{3}A}+\overrightarrow{G_{3}C}\\\\&=&\underbrace{-3\overrightarrow{G_{3}B}+2\overrightarrow{G_{3}A}}_{=\vec{0}}+\overrightarrow{G_{3}C}\\\\&=&\overrightarrow{G_{2}C}\end{array}
 
D'où, \boxed{\overrightarrow{f(M)}=\overrightarrow{G_{3}C}}
 
Montre que les droites (AG_{1})\;,\ (BG_{2})\ et \ (CG_{3}) sont parallèles.
 
D'après les résultats des questions précédentes, on peut écrire :
\left\lbrace\begin{array}{rcl}\overrightarrow{f(M)}&=&2\overrightarrow{G_{1}A}\\\\\overrightarrow{f(M)}&=&3\overrightarrow{BG_{2}}\\\\\overrightarrow{f(M)}&=&\overrightarrow{G_{3}C}\end{array}\right.
Ce qui entraine : \boxed{2\overrightarrow{G_{1}A}=3\overrightarrow{BG_{2}}=\overrightarrow{G_{3}C}}
 
D'où, les vecteurs 2\overrightarrow{G_{1}A}\;,\ 3\overrightarrow{BG_{2}}\ et \ \overrightarrow{G_{3}C} sont colinéaires.
 
Par conséquent, les droites (AG_{1})\;,\ (BG_{2})\ et \ (CG_{3}) sont parallèles.
 
5) En déduisons une construction de G_{3}.
 
En effet, G_{3} étant le barycentre de (B\;;\ -3)\ et \ (A\;;\ 2) alors, A\;,\ B\ et \ G_{3} sont alignés.
 
D'où, G_{3} appartient à la droite (AB).
 
Par ailleurs, G_{3}\in(CG_{3}).
 
Donc, les droites (AB)\ et \ (CG_{3}) sont sécantes en G_{3}.
 
L'autre information capitale est : les droites (AG_{1})\;,\ (BG_{2})\ et \ (CG_{3}) sont parallèles.
 
Ainsi, pour construire G_{3}, on trace la droite parallèle à (AG_{1}) et passant par le point C.
 
Cette droite coupe donc la droite (AB) au point G_{3}.

 

Exercice 23

Soit un triangle ABC rectangle en A et tel que AB=4\;,\ AC=6.
 
1) Plaçons le point G tel que :
\overrightarrow{AG}=\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}
2) Calculons AG.
 
Comme \overrightarrow{AG}=\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC} alors, on a :
 
\begin{array}{rcl}\left\|\overrightarrow{AG}\right\|^{2}&=&\left\|\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right\|^{2}\\\\&=&\left\|\overrightarrow{AB}\right\|^{2}+\left\|\dfrac{1}{2}\overrightarrow{AC}\right\|^{2}+2\times\left\|\overrightarrow{AB}\right\|\times\left\|\dfrac{1}{2}\overrightarrow{AC}\right\|\times\cos\widehat{A}\\\\&=&\left\|\overrightarrow{AB}\right\|^{2}+\dfrac{1}{4}\left\|\overrightarrow{AC}\right\|^{2}+2\times\left\|\overrightarrow{AB}\right\|\times\dfrac{1}{2}\left\|\overrightarrow{AC}\right\|\times\underbrace{\cos\dfrac{\pi}{2}}_{=0}\\\\&=&\left\|\overrightarrow{AB}\right\|^{2}+\dfrac{1}{4}\left\|\overrightarrow{AC}\right\|^{2}\end{array}
 
Par conséquent, \boxed{\left\|\overrightarrow{AG}\right\|=\sqrt{\left\|\overrightarrow{AB}\right\|^{2}+\dfrac{1}{4}\left\|\overrightarrow{AC}\right\|^{2}}\qquad(1)}
 
Ainsi, en remplaçant AB\ et \ AC par leur valeur, dans la relation (1), on obtient :
 
\begin{array}{rcl}\left\|\overrightarrow{AG}\right\|&=&\sqrt{\left\|\overrightarrow{AB}\right\|^{2}+\dfrac{1}{4}\left\|\overrightarrow{AC}\right\|^{2}}\\\\&=&\sqrt{4^{2}+\dfrac{1}{4}\times 6^{2}}\\\\&=&\sqrt{16+\dfrac{36}{4}}\\\\&=&\sqrt{16+9}\\\\&=&\sqrt{25}\\\\&=&5\end{array}
 
D'où, \boxed{AG=5}
 
3) Démontrons que G est le barycentre de A\;,\ B\;,\ C affectés de coefficients que l'on précisera.
 
Soit : \overrightarrow{AG}=\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}
 
Ce qui entraine : \overrightarrow{AG}-\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AC}=\vec{0}
 
Ce qui peut encore s'écrire, en multipliant par 2\ :
2\overrightarrow{AG}-2\overrightarrow{AB}-\overrightarrow{AC}=\vec{0}
Alors, par la relation de Chasles, introduisons le point G dans les vecteurs \overrightarrow{AB}\ et \ \overrightarrow{AC}.
 
On obtient :
 
\begin{array}{rcl}2\overrightarrow{AG}-2\overrightarrow{AB}-\overrightarrow{AC}=\vec{0}&\Leftrightarrow&2\overrightarrow{AG}-2\left(\overrightarrow{AG}+\overrightarrow{GB}\right)-\left(\overrightarrow{AG}+\overrightarrow{GC}\right)=\vec{0}\\\\&\Leftrightarrow&2\overrightarrow{AG}-2\overrightarrow{AG}-2\overrightarrow{GB}-\overrightarrow{AG}-\overrightarrow{GC}=\vec{0}\\\\&\Leftrightarrow&-\overrightarrow{AG}+2\overrightarrow{BG}+\overrightarrow{CG}=\vec{0}\end{array}
 
Ainsi, \boxed{-\overrightarrow{AG}+2\overrightarrow{BG}+\overrightarrow{CG}=\vec{0}}
 
Par conséquent, G est barycentre de (A\;;\ -1)\;,\ (B\;;\ 2)\ et \ (C\;;\ 1).
 
4) Déterminons l'ensemble (\Gamma) des points M du plan tels que :
\left\|-\overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC}\right\|=10\qquad(2)
D'après le résultat de la question 3\;)\;,\ G est barycentre de (A\;;\ -1)\;,\ (B\;;\ 2)\ et \ (C\;;\ 1).
 
Donc, d'après la propriété caractéristique, on a : 
\left\|-\overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC}\right\|=\left\|2\overrightarrow{MG}\right\|
Ainsi, dans la relation (2), en remplaçant \left\|-\overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC}\right\| par \left\|2\overrightarrow{MG}\right\|, on obtient :
 
\begin{array}{rcl}\left\|-\overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC}\right\|=10&\Leftrightarrow&\left\|2\overrightarrow{MG}\right\|=10\\\\&\Leftrightarrow&2\left\|\overrightarrow{MG}\right\|=10\\\\&\Leftrightarrow&\left\|\overrightarrow{MG}\right\|=\dfrac{10}{2}\\\\&\Leftrightarrow&\left\|\overrightarrow{MG}\right\|=5\end{array}
 
D'où, \boxed{\left\|\overrightarrow{MG}\right\|=5}
 
Ce qui représente le cercle de centre G et de rayon 5.
 
Par conséquent, l'ensemble (\Gamma) des points M du plan tels que \left\|-\overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC}\right\|=10 est le cercle de centre G et de rayon 5.
 
5) Montrons que (\Gamma) passe par C\ et \ A.
 
En effet, (\Gamma) passe par C\ et \ A si, et seulement si, CG=5\ et \ AG=5.
 
Or, d'après le résultat de la question 2\;), on a :
AG=5
Par conséquent, (\Gamma) passe par A.
 
Calculons CG
 
Pour cela, exprimons d'abord \overrightarrow{CG} en fonction de \overrightarrow{AB}\ et \ \overrightarrow{AC}.
 
D'après la question 1\;), on a : \overrightarrow{AG}=\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}
 
Alors, par la relation de Chasles, en introduisant le point C dans le vecteur \overrightarrow{AG}, on obtient :
 
\begin{array}{rcl}\overrightarrow{AG}=\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}&\Rightarrow&\overrightarrow{AC}+\overrightarrow{CG}=\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\\\\&\Rightarrow&\overrightarrow{CG}=\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}-\overrightarrow{AC}\\\\&\Rightarrow&\overrightarrow{CG}=\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AC}\end{array}
 
Donc, \boxed{\overrightarrow{CG}=\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AC}}
 
Par suite,
 
\begin{array}{rcl}\left\|\overrightarrow{CG}\right\|^{2}&=&\left\|\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AC}\right\|^{2}\\\\&=&\left\|\overrightarrow{AB}\right\|^{2}+\left\|\dfrac{1}{2}\overrightarrow{AC}\right\|^{2}-2\times\left\|\overrightarrow{AB}\right\|\times\left\|\dfrac{1}{2}\overrightarrow{AC}\right\|\times\cos\widehat{A}\\\\&=&\left\|\overrightarrow{AB}\right\|^{2}+\dfrac{1}{4}\left\|\overrightarrow{AC}\right\|^{2}-2\times\left\|\overrightarrow{AB}\right\|\times\dfrac{1}{2}\left\|\overrightarrow{AC}\right\|\times\underbrace{\cos\dfrac{\pi}{2}}_{=0}\\\\&=&\left\|\overrightarrow{AB}\right\|^{2}+\dfrac{1}{4}\left\|\overrightarrow{AC}\right\|^{2}\end{array}
 
Par conséquent,
\left\|\overrightarrow{CG}\right\|=\sqrt{\left\|\overrightarrow{AB}\right\|^{2}+\dfrac{1}{4}\left\|\overrightarrow{AC}\right\|^{2}}=\left\|\overrightarrow{AG}\right\|
D'où, \boxed{CG=5}
 
Ce qui montre que (\Gamma) passe aussi par le point C.

 
 
 

Exercice 24

Soit ABCD un rectangle. On note I le milieu de [AB]\;,\ J milieu de [BC]\ et \ E le centre de gravité du triangle ABC.
 
Soient F\ et \ G tels que F barycentre de (C\;;\ 1)\;,\ (D\;;\ 3)\ et \ G barycentre de (E\;;\ 3)\;,\ (D\;;\ 3)
 
1) Construisons F.
 
F barycentre de (C\;;\ 1)\;,\ (D\;;\ 3) alors, d'après la propriété caractéristique, on a :
\overrightarrow{DF}=\dfrac{1}{4}\overrightarrow{DC}
2) Montrons que G est milieu de [ED].
 
On a : G barycentre de (E\;;\ 3)\;,\ (D\;;\ 3).
 
Or, E\ et \ D ont même coefficient de pondération qui est égal à 3.
 
Par conséquent, G est le milieu de [ED].
 
Construisons G.
 
En effet, G milieu de [ED] alors, on a :
\overrightarrow{DG}=\dfrac{1}{2}\overrightarrow{DE}
3) Démontrons que G est le barycentre de (A\;,\ 1)\;,\ (B\;,\ 1)\;,\ (C\;,\ 1)\ et \ (D\;,\ 3)
 
On a : G barycentre de (E\;;\ 3)\;,\ (D\;;\ 3).
 
Or, E est le centre de gravité du triangle ABC.
 
Ce qui signifie que E est l'isobarycentre des points A\;,\ B\;,\ C.
 
Par conséquent, E est barycentre de (A\;,\ 1)\;,\ (B\;,\ 1)\;,\ (C\;,\ 1).
 
Ainsi, par la réciproque de la propriété d'associativité du barycentre, on a : G barycentre de (A\;,\ 1)\;,\ (B\;,\ 1)\;,\ (C\;,\ 1)\ et \ (D\;,\ 3)
 
Autre méthode
 
On a : G est milieu de [ED].
 
Donc,
\overrightarrow{EG}=\overrightarrow{GD}
Par ailleurs, comme E est le centre de gravité du triangle ABC alors, E est barycentre de (A\;,\ 1)\;,\ (B\;,\ 1)\;,\ (C\;,\ 1).
 
D'où,
\overrightarrow{EA}+\overrightarrow{EB}+\overrightarrow{EC}=\vec{0}
Ainsi, par la relation de Chasles, introduisons le point G dans les vecteurs \overrightarrow{EA}\;,\ \overrightarrow{EB}\ et \ \overrightarrow{EC}
 
On obtient alors :
 
\begin{array}{rcl}\overrightarrow{EA}+\overrightarrow{EB}+\overrightarrow{EC}=\vec{0}&\Leftrightarrow&\left(\overrightarrow{EG}+\overrightarrow{GA}\right)+\left(\overrightarrow{EG}+\overrightarrow{GB}\right)+\left(\overrightarrow{EG}+\overrightarrow{GC}\right)=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{EG}+\overrightarrow{GA}+\overrightarrow{EG}+\overrightarrow{GB}+\overrightarrow{EG}+\overrightarrow{GC}=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+3\overrightarrow{EG}=\vec{0}\end{array}
 
Or, on sait que : \overrightarrow{EG}=\overrightarrow{GD}
 
Donc, en remplaçant \overrightarrow{EG} par \overrightarrow{GD}, on obtient :
\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+3\overrightarrow{EG}=\vec{0}\ \Leftrightarrow\ \overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+3\overrightarrow{GD}=\vec{0}
D'où, \boxed{\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+3\overrightarrow{GD}=\vec{0}}
 
Ce qui montre que G est le barycentre de (A\;,\ 1)\;,\ (B\;,\ 1)\;,\ (C\;,\ 1)\ et \ (D\;,\ 3).
 
4) Démontrons que G appartient à la droite (IF).
 
D'après le résultat de la question 3\;), on a : G barycentre de (A\;,\ 1)\;,\ (B\;,\ 1)\;,\ (C\;,\ 1)\ et \ (D\;,\ 3).
 
Or, F est le barycentre de (C\;;\ 1)\;,\ (D\;;\ 3).
 
Donc, en appliquant la propriété d'associativité du barycentre, on obtient : G barycentre de (A\;,\ 1)\;,\ (B\;,\ 1)\;,\ (F\;,\ 4).
 
Par ailleurs, I étant milieu de [AB] alors, I est barycentre de (A\;,\ 1)\;,\ (B\;,\ 1).
 
Ainsi, d'après la propriété d'associativité du barycentre, on a : G barycentre de (I\;,\ 2)\;,\ (F\;,\ 4).
 
Par conséquent, les points G\;,\ I\ et \ F sont alignés.
 
D'où, G appartient à la droite (IF).
 
5) Soit K le point défini par : \overrightarrow{AK}=\dfrac{3}{4}\overrightarrow{AD}
 
Montrons que G\;,\ K\ et \ J sont alignés.
 
On a :
 
\begin{array}{rcl}\overrightarrow{AK}=\dfrac{3}{4}\overrightarrow{AD}&\Leftrightarrow&4\overrightarrow{AK}=3\overrightarrow{AD}\\\\&\Leftrightarrow&4\overrightarrow{AK}-3\overrightarrow{AD}=\vec{0}\\\\&\Leftrightarrow&4\overrightarrow{AK}-3\left(\overrightarrow{AK}+\overrightarrow{KD}\right)=\vec{0}\\\\&\Leftrightarrow&4\overrightarrow{AK}-3\overrightarrow{AK}-3\overrightarrow{KD}=\vec{0}\\\\&\Leftrightarrow&\overrightarrow{AK}+3\overrightarrow{DK}=\vec{0}\end{array}
 
Ainsi, \boxed{\overrightarrow{AK}+3\overrightarrow{DK}=\vec{0}}
 
Ce qui signifie que K est le barycentre de  (A\;,\ 1)\;,\ (D\;,\ 3).
 
Or, G est le barycentre de (A\;,\ 1)\;,\ (B\;,\ 1)\;,\ (C\;,\ 1)\ et \ (D\;,\ 3).
 
Donc, par associativité du barycentre, on a : G est le barycentre de (B\;,\ 1)\;,\ (C\;,\ 1)\;,\ (K\;,\ 4).
 
Par ailleurs, comme J est le milieu de [BC] alors, J est barycentre de (B\;,\ 1)\;,\ (C\;,\ 1).
 
Ainsi, d'après la propriété d'associativité du barycentre, G est barycentre de (J\;,\ 2)\;,\ (K\;,\ 4).
 
D'où, les points G\;,\ K\ et \ J sont alignés.

 
 

Exercice 26

Soit un triangle ABC tel que :
AB=6\;cm\;,\ BC=4\;cm\ \text{ et }\ AC=5\;cm
1) Construisons I\ et \ J tels que I soit barycentre de (A\;;\ 1)\;,\ (B\;;\ 1)\;,\ (C\;;\ 2)\ et \ J barycentre de (A\;;\ 2)\;,\ (B\;;\ 3)\;,\ (C\;;\ -1).
 
En effet, soit I barycentre de (A\;;\ 1)\;,\ (B\;;\ 1)\;,\ (C\;;\ 2) alors, d'après la propriété caractéristique, on a :
 
\begin{array}{rcl}\overrightarrow{AI}&=&\dfrac{\overrightarrow{AB}+2\overrightarrow{AC}}{4}\\\\&=&\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\end{array}
 
De la même manière, J étant barycentre de (A\;;\ 2)\;,\ (B\;;\ 3)\;,\ (C\;;\ -1) alors, d'après la propriété caractéristique, on obtient :
 
\begin{array}{rcl}\overrightarrow{AJ}&=&\dfrac{3\overrightarrow{AB}-\overrightarrow{AC}}{4}\\\\&=&\dfrac{3}{4}\overrightarrow{AB}-\dfrac{1}{4}\overrightarrow{AC}\end{array}
 
Enfin, plaçons les point I\ et \ J tels que :
\overrightarrow{AI}=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\quad\text{ et }\quad\overrightarrow{AJ}=\dfrac{3}{4}\overrightarrow{AB}-\dfrac{1}{4}\overrightarrow{AC}
Autre méthode
 
Pour une construction plus simple, on peut toujours essayer de chercher des barycentres partiels et par la suite appliquer la propriété d'associativité du barycentre.
 
En effet, soit I barycentre de (A\;;\ 1)\;,\ (B\;;\ 1)\;,\ (C\;;\ 2) alors, choisissons K barycentre de (A\;;\ 1)\;,\ (B\;;\ 1).
 
A\ et \ B ayant la même pondération alors, K est milieu de [AB].
 
Par suite, d'après la propriété d'associativité du barycentre, I est barycentre de (K\;;\ 2)\;,\ (C\;;\ 2).
 
Comme K\ et \ C sont affectés d'un même coefficient alors, I est le milieu de [KC].
 
Par ailleurs, pour la construction du point J, nous pouvons, par exemple, commencer par construire un point E barycentre de (B\;;\ 3)\;,\ (C\;;\ -1).
 
Ensuite, par application de la propriété d'associativité du barycentre, J sera barycentre de (A\;;\ 2)\;,\ (E\;;\ 2).
 
Comme A\ et \ E sont affectés d'un même coefficient alors, J est le milieu de [AE].
 
2) Déterminons l'ensemble des points M du plan tels que \|\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}\|=\|2\overrightarrow{MA}+3\overrightarrow{MB}-\overrightarrow{MC}\|\qquad(1)
 
En effet, I étant barycentre de (A\;;\ 1)\;,\ (B\;;\ 1)\;,\ (C\;;\ 2) alors, d'après la propriété caractéristique, on a :
\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=4\overrightarrow{MI}
Aussi, comme J est le barycentre de (A\;;\ 2)\;,\ (B\;;\ 3)\;,\ (C\;;\ -1) alors, d'après la propriété caractéristique, on obtient :
2\overrightarrow{MA}+3\overrightarrow{MB}-\overrightarrow{MC}=4\overrightarrow{MJ}
Ainsi, dans la relation (1), en remplaçant \overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC} par 4\overrightarrow{MI}\ et \ 2\overrightarrow{MA}+3\overrightarrow{MB}-\overrightarrow{MC} par 4\overrightarrow{MJ}, on obtient :
 
\begin{array}{rcl} \|\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}\|=\|2\overrightarrow{MA}+3\overrightarrow{MB}-\overrightarrow{MC}\|&\Leftrightarrow&\|4\overrightarrow{MI}\|=\|4\overrightarrow{MJ}\|\\ \\ &\Leftrightarrow&\|\overrightarrow{MI}\|=\|\overrightarrow{MJ}\|\end{array}
 
Donc, \boxed{\|\overrightarrow{MI}\|=\|\overrightarrow{MJ}\|}
 
Ce qui représente la médiatrice de [IJ]
 
D'où, l'ensemble des points M du plan tels que \|\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}\|=\|2\overrightarrow{MA}+3\overrightarrow{MB}-\overrightarrow{MC}\| est la médiatrice du segment [IJ].
 
3) Déterminons l'ensemble des points M du plan tels que \|\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}\|=\|\overrightarrow{MB}-\overrightarrow{MC}\|\qquad(2)
 
En effet, soit I barycentre de (A\;;\ 1)\;,\ (B\;;\ 1)\;,\ (C\;;\ 2) alors, d'après la propriété caractéristique, on a :
\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=4\overrightarrow{MI}
Par ailleurs, en utilisant les propriétés du calcul vectoriel puis, la relation de Chasles, on a :
\overrightarrow{MB}-\overrightarrow{MC}=\overrightarrow{CM}+\overrightarrow{MB}=\overrightarrow{CB}
Donc, dans la relation (2), en remplaçant \overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC} par 4\overrightarrow{MI}\ et \ \overrightarrow{MB}-\overrightarrow{MC} par \overrightarrow{CB}, on obtient :
 
\begin{array}{rcl} \|\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}\|=\|\overrightarrow{MB}-\overrightarrow{MC}\|&\Leftrightarrow&\|4\overrightarrow{MI}\|=\|\overrightarrow{CB}\|\\ \\ &\Leftrightarrow&\|\overrightarrow{MI}\|=\dfrac{\|\overrightarrow{CB}\|}{4}\end{array}
 
Or, on sait que BC=4\;cm donc, \|\overrightarrow{MI}\|=\dfrac{4}{4}=1
 
D'où, \boxed{\|\overrightarrow{MI}\|=1}
 
On obtient alors le cercle de centre I et de rayon 1\;cm.
 
Ainsi, l'ensemble des points M du plan tels que \|\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}\|=\|\overrightarrow{MB}-\overrightarrow{MC}\| est le cercle de centre I et de rayon 1\;cm.

 

Exercice 28

Soit trois points A\;,\ B\;,\ C non alignés ; à tout réel m on associe le point G_{m} s'il existe, barycentre de \{(A\;;\ 2)\;,\ (B\;;\ 1)\;,\ (C\;;\ m)\}
 
1) Déterminons les valeurs de m pour lesquelles il existe un barycentre G_{m}.
 
G_{m} existe si, et seulement si, la somme des coefficients de pondération des points A\;,\ B\;,\ C est non nulle.
 
Ainsi,
 
\begin{array}{rcl}G_{m}\ \exists&\Leftrightarrow&2+1+m\neq 0\\\\&\Leftrightarrow&3+m\neq 0\\\\&\Leftrightarrow&m\neq -3\end{array}
 
Donc, pour tout nombre réel m différent de -3, le barycentre G_{m} existe.
 
2) Construisons les points G_{0}\;,\ G_{1}\ et \ G_{-1} respectivement associés à 0\;,\ 1\ et \ -1.
 
Soit G_{0} barycentre de \{(A\;;\ 2)\;,\ (B\;;\ 1)\;,\ (C\;;\ 0)\} alors, on a :
2\overrightarrow{G_{0}A}+\overrightarrow{G_{0}B}+0\times\overrightarrow{G_{0}C}=\vec{0}
Ce qui peut encore s'écrire :
2\overrightarrow{G_{0}A}+\overrightarrow{G_{0}B}=\vec{0}
Ainsi, G_{0} est barycentre de \{(A\;;\ 2)\;,\ (B\;;\ 1)\}.
 
Donc, d'après la propriété caractéristique, on a :
\overrightarrow{AG_{0}}=\dfrac{1}{3}\overrightarrow{AB}
Soit G_{1} barycentre de \{(A\;;\ 2)\;,\ (B\;;\ 1)\;,\ (C\;;\ 1)\} alors, en appliquant la propriété caractéristique on obtient :
\overrightarrow{AG_{1}}=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}
Soit G_{-1} barycentre de \{(A\;;\ 2)\;,\ (B\;;\ 1)\;,\ (C\;;\ -1)\} alors, d'après la propriété caractéristique on a :
\overrightarrow{AG_{-1}}=\dfrac{1}{3}\overrightarrow{AB}-\dfrac{1}{3}\overrightarrow{AC}
Nous constatons que les points G_{0}\;,\ G_{1}\;,\ G_{-1}\ et \ C sont alignés.
 
Ce qui signifie que ces points sont sur une même droite.
 
3) Démontrons que lorsque m varie, G_{m} se déplace sur une droite fixe.
 
Soit G_{m} barycentre du système \{(A\;;\ 2)\;,\ (B\;;\ 1)\;,\ (C\;;\ m)\}.
 
Considérons I barycentre de \{(A\;;\ 2)\;,\ (B\;;\ 1)\}.
 
Alors, en appliquant la propriété d'associativité du barycentre, on obtient : G_{m} barycentre du système \{(I\;;\ 3)\;,\ (C\;;\ m)\}.
 
D'où, les points G_{m}\;,\ I\ et \ C sont alignés.
 
Par conséquent G_{m} appartient à la droite (CI).
 
Ainsi, lorsque m varie, G_{m} se déplace sur une droite fixe ; (CI).
 
Remarque : I\ et \ G_{0} sont confondus.

 

 
 
Auteur: 
Diny Faye

Commentaires

Anonyme (non vérifié)

mar, 07/06/2021 - 18:34

interressant

ibrahima sow (non vérifié)

lun, 03/14/2022 - 02:34

intéressant

Anonyme (non vérifié)

sam, 12/24/2022 - 08:57

Correction de l exo 14

Cheikh2216620000 (non vérifié)

mer, 01/03/2024 - 22:58

Bonjour je suis un élève 1s

Anonyme (non vérifié)

mar, 01/10/2023 - 22:38

Montrer la correction d'exercice 21 ou 22,27 ou 33

Djigo (non vérifié)

dim, 11/19/2023 - 14:49

Merci de votre travail pour aider les élèves

Maye faye (non vérifié)

dim, 01/21/2024 - 22:04

Tellement intéressant

Mouhamed Ndiaye (non vérifié)

jeu, 02/22/2024 - 00:00

Pouvez vous me donner la correction de l'exercice 21 sur le barycentre

Jalilo (non vérifié)

lun, 03/04/2024 - 03:19

Très bien, svp Ex 14

Jalilo (non vérifié)

lun, 03/04/2024 - 03:19

Merci bcp

Anonyme (non vérifié)

ven, 12/27/2024 - 19:33

Correction de l'exo 15 svp

Angèle sene (non vérifié)

ven, 12/27/2024 - 19:37

La correction d'exo 15

Anonyme (non vérifié)

ven, 02/07/2025 - 18:27

Merci beaucoup

Ajouter un commentaire