Vous êtes ici

Série d'exercices Effet photoélectrique - Ts

Classe:

Terminale

Exercice 1

Une surface métallique est éclairé par la lumière

$UV$ de longueur d'onde

$\lambda=0.150\mu m.$

Elle émet des électrons dont l'énergie cinétique maximale à

$4.8eV.$

a) Calculer le travail d'extraction

$W_{0}$

b) Quelle est la nature du métal ?

$\begin{array}{|c|c|} \hline \text{Métal}&\text{Seuil photoélectrique }\lambda_{0}(\mu m)\\ \hline Zn&0.35\\ \hline Al&0.365\\ \hline Na&0.50\\ \hline K&0.55\\ \hline Sr&0.60\\ \hline Cs&0.66\\ \hline \end{array}$

c) Quelle tension serait nécessaire pour arrêter cette émission

d) Pour augmenter la vitesse maximale d'émission, faut-il changer sa longueur d'onde ?

Exercice 2

1) Décrire une cellule photoélectrique dite cellule photoémissive à vide

Dessiner un schéma de montage à réaliser pour mettre en évidence l'effet photoélectrique en utilisant cette cellule

2) La longueur d'onde correspondante au seuil photoélectrique d'une photocathode émissive au césium est

$\lambda_{0}=0.66\cdot10^{-6}m$

a) Quelle est en joules et en

$eV$ l'énergie d'extraction

$W_{0}$ d'un électron ?

Exprimer cette énergie en

$eV$

b) La couche de césium reçoit une radiation monochromatique de longueur d'onde

$\lambda=0.44\cdot10^{-6}m$

Déterminer l'énergie cinétique maximale

$E_{c}$ d'un électron émis au niveau de la cathode.

L'exprimer en joules puis en

$eV.$

Exercice 3

On utilise une cellule photoélectrique au césium

Pour différentes radiations incidentes, on mesure la tension qui annule le courant photoélectrique (Tension d'arrêt)

Les résultats sont les suivants :

$\begin{array}{|c|c|c|c|c|} \hline \lambda(\mu m)&0.60&0.50&0.40&0.30\\ \hline U(V)&0.19&0.60&1.22&2.26\\ \hline \end{array}$

1) Exprimer l'énergie cinétique de l'électron au départ de la couche photoémissive en fonction de la fréquence

$ѵ$ et du travail d'extraction

$W_{0}$

2) Faire le schéma du montage utilisé

Exprimer la tension d'arrêt en fonction de

$ѵ$ et

$W_{0}$

3) Calculer les fréquences

$ѵ$ des radiations utilisées

4) Tracer la courbe représentant la fonction

$U=f(ѵ)$ et en déduire la fréquence

$ѵ_{0}$ du seuil photoélectrique du césium, ainsi que la longueur d'onde

$\lambda_{0}$ correspondante

Exercice 4

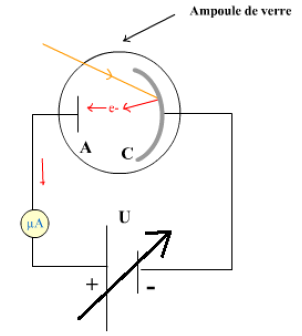
On réalise le montage suivant avec une cellule photoémissive à vide éclairée par une lumière monochromatique de fréquence (schéma)

Pour chaque valeur de

$ѵ_{i}$ , la tension

$U_{CA}$ entre cathode et anode est réglée à la valeur

$U_{0}$ juste nécessaire pour l'intensité

$i$ traversant la cellule.

Le voltmètre indique alors

$U_{0}$

On obtient les valeurs suivantes :

$\begin{array}{|c|c|c|c|c|c|} \hline V(Hz)&6\cdot10^{14}&7\cdot10^{14}&8\cdot10^{14}&9\cdot10^{14}&10\cdot10^{14}\\ \hline U_{0}(V)&0.4&0.8&1.24&1.66&2.08\\ \hline \end{array}$

1) Rappeler : l'expression de l'énergie d'un photon de fréquence

$ѵ$ ; l'expression de l'énergie maximale des électrons émis par la cathode en fonction de

$U_{0}$

En déduire la relation existant entre

$ѵ$ ,

$U_{0}$ ,

$h$ (constante de Planck),

$e$ et

$W_{0}$ travail d'extraction correspondant à la cellule utilisée

2) Faire la représentation graphique des variations de

$U_{0}$ en fonction de

$ѵ$

Abscisses :

$1cm$ pour

$1014Hz$ ;

ordonnées :

$1cm$ pour

$0.2V$

En déduire le seuil de fréquence

$ѵ_{0}$ de la cellule, la constante de Planck

$h$ et

$W_{0}$ (exprimé en électron-volt)

Exercice 5

La charge de l'électron est

$-e=-1.6\cdot10^{-19}C.$

On éclaire une cellule photoélectrique par un faisceau lumineux monochromatique de fréquence

$ѵ$ et on mesure le potentiel d'arrêt

$U_{0}$ de la cellule.

1) Faire un schéma du montage utilisé

2) On répète l'opération en utilisant diverses radiations et on obtient les résultats suivants :

$\begin{array}{|c|c|c|c|c|c|c|c|c|} \hline V(Hz)&5.18\cdot10^{14}&5.49\cdot10^{14}&5.88\cdot10^{14}&6.17\cdot10^{14}&6.41\cdot10^{14}&6.78\cdot10^{14}&6.91\cdot10^{14}&7.31\cdot10^{14}\\ \hline U_{0}(V)&0.042&0.171&0.332&0.452&0.56&0.706&0.758&0.924\\ \hline \end{array}$

Tracer sur papier millimétré, le graphe

$U_{0}=f(ѵ)$ en utilisant les échelles suivantes :

$10cm$ pour

$1V$ ;

$2cm$ pour

$1014Hz.$

3) Rappeler la relation entre le potentiel d'arrêt, le travail d'extraction

$W_{0}$ , d'un électron du métal de la cathode et l'énergie des photons incidents

4) Déterminer à l'aide du graphique :

a) La constante de Planck

b) Le travail d'extraction d'un électron du métal de la cathode.

5) Citer autre phénomène qui, comme l'effet photoélectrique la nature corpusculaire de la lumière.

Quelle caractéristique du photon met-il en évidence

Exercice 6

La courbe de la figure ci-dessous représente les variations de

$|U_{0}|$ en fonction de

$\dfrac{1}{\lambda}$

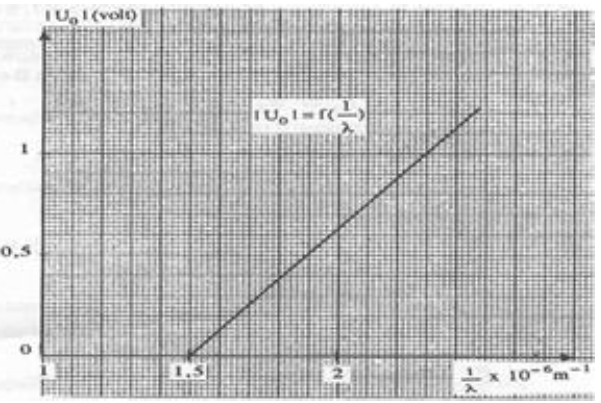
$|U_{0}|$ désigne la valeur absolue du potentiel d'arrêt d'une cellule photoélectrique et

$\lambda$ , la longueur d'onde de la radiation monochromatique qui éclaire la cathode de la cellule.

1) Déterminer graphiquement l'équation de la courbe représentant

$|U_{0}|=f\left(\dfrac{1}{\lambda}\right)$

2) a) Établir la relation entre le potentiel d'arrêt

$U_{0}$ , le travail d'extraction

$W_{0}$ d'un électron du métal de la cathode et l'énergie

$W$ d'un photon incident.

En déduire l'expression de

$|U_{0}|$ en fonction de

b) En identifiant la relation précédente à celle trouvée graphiquement dans la première question, déterminer une valeur approchée de la constante de Planck

$h$ et calculer

$W_{0}.$

3) On éclaire maintenant la cellule photoélectrique par une lumière monochromatique de longueur d'onde

$\lambda=0.588\mu m.$

a) Calculer, dans le système international d'unités, l'énergie

$W$ et la quantité de mouvement

$\|\overrightarrow{P}\|$ en

$MeV\cdot c^{-1}$

b) A l'aide de la courbe représentant

$|U_{0}|=\left(\dfrac{1}{\lambda}\right)$ , calculer le potentiel d'arrêt

$U_{0}$ correspondant et en déduire la valeur de l'énergie cinétique maximale des électrons émis par la cathode.

c) En supposant relativiste toute particule animée, dans un repère galiléen, d'une vitesse supérieure à

$0.14c$ , montrer que l'énergie cinétique d'une telle particule doit être supérieure à une fraction minimale

$x$ de son énergie au repos.

Calculer

$x.$

En déduire si les électrons émis par la cathode sont relativistes ou non.

d) Calculer alors la vitesse maximale d'émission d'un électron par la cathode.

On donne :

$\ast\$ La célérité de la lumière dans le vide :

$c=3\cdot10^{8}m\cdot s^{-1}$

$\ast\$ La masse d'un électron :

$m=9.1\cdot10^{-19}C.$

$\ast\$ La constante de Planck :

$h=6.62\cdot10^{-34}Js$

Exercice 7

Une cellule photoélectrique comporte une cathode

$(C)$ constituée d'une surface métallique dont l'énergie d'extraction est

$W_{0}=2.5eV.$

Un dispositif expérimental permet d'éclairer

$(C)$ avec l'une des radiations de longueur d'onde :

$623.6nm$ ;

$413.7nm$ ;

$560.0nm$ ;

$451.4nm.$

1) Quelle est la valeur

$\lambda_{0}$ de la longueur d'onde du seuil photoélectrique ?

2) Parmi les quatre radiations monochromatiques considérées, deux seulement de longueur d'onde

$\lambda_{1}$ et

$\lambda_{2}$ peuvent extraire des électrons du métal et leur communiquer une énergie cinétique.

a) Donner les valeurs de

$\lambda_{1}$ et

$\lambda_{2}$ ?

b) Montrer que l'expression du potentiel d'arrêt s'écrit

$U_{0}=-\dfrac{E_{c}}{e}$ où

$E_{c}$ est l'énergie cinétique de l'électron émis et

$(-e)$ sa charge électrique.

c) Calculer la valeur du potentiel d'arrêt correspondant à chacune des deux radiations de longueur d'onde

$\lambda_{1}$ et

$\lambda_{2}$ capables d'extraire un électron du métal et lui communiquer une énergie cinétique.

3) On éclaire simultanément la cathode

$(C)$ par les des deux radiations de longueur d'onde

$\lambda_{1}$ et

$\lambda_{2}.$

Déterminer, en le justifiant, la valeur du potentiel d'arrêt correspondant à cette expérience.

Données :

constante de Planck

$h=6.62\cdot10^{-34}J\cdot s$

charge d'un électron

$-e=-1.6\cdot10^{-19}C$

célérité de la lumière

$c=3\cdot10^{8}m\cdot s$

$-11nm=10^{-9} m.$

$1eV=1.6\cdot10^{-19}J$

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

Auteur:

Amary Thiam & Sidy Mouhamed Ndiaye

Commentaires

Anonyme (non vérifié)

jeu, 03/31/2022 - 23:33

Permalien

correction?

répondre

Zakia (non vérifié)

ven, 05/27/2022 - 15:07

Permalien

Corrigé

Exercice 1

répondre

Anonyme (non vérifié)

lun, 04/18/2022 - 10:58

Permalien

La correction

répondre

Anonyme (non vérifié)

lun, 04/18/2022 - 10:59

Permalien

J'ai besoin la correction

répondre

Latyr ngom (non vérifié)

mer, 05/25/2022 - 17:44

Permalien

On a besoin du correction

répondre

Sanae najmi (non vérifié)

dim, 05/14/2023 - 21:12

Permalien

physique

bonjour

répondre

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Série d'exercices Effet photoélectrique - Ts

Formulaire de recherche

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Exercice 5

Exercice 6

Exercice 7

▸\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}

Commentaires

correction?

Corrigé

La correction

J'ai besoin la correction

On a besoin du correction

physique

Ajouter un commentaire

Plain text

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$