Série d'exercices : Loi de Laplace - Ts
Classe:
Terminale
Exercice 1
Une tige en cuivre $OM$ parcourue par un courant de haut en bas d'intensité $I_{1}=7A$ peut articuler librement en $« O »$ et son extrémité $M$ touche une solution conductrice.
On approche d'elle une deuxième tige $AN$ en cuivre de longueur $L=12\,cm$ qui peut articuler librement en $A$ et son extrémité $N$ touche une solution conductrice voir (figure 1).
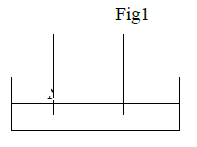
Lorsque la tige $AN$ est parcourue par un courant $OA$
De haut en bas d'intensité $I_{2}=5A$ sa partie inférieure de longueur $l=4\,cm$ plonge dans le champ magnétique $\overrightarrow{B_{1}}$ $MN$ uniforme, perpendiculaire au plan de la feuille, de sens sortant et de valeur $0.3T.$
1) donner le sens d'inclinaison de la tige $AN.$
2) a) donner les caractéristiques de la force de la place $\overrightarrow{F}$ qui agit sur la tige $AN$
b) représenter $\overrightarrow{F}$
c) déterminer la masse de la tige $AN$, sachant qu'elle s'écarte de la verticale d'un angle $\theta=10^{\circ}.$
On donne $g=10\,N\cdot Kg^{-1}.$
3) La partie supérieure de la tige $OM$ de longueur $l'=3\,cm$ plonge dans le champ magnétique $\overrightarrow{B_{2}}$ uniforme, normale au plan de la feuille et de sens rentrant crée par la tige $AN.$
a) est-ce que il y a une interaction entre les deux tiges ?
Expliquer
b) quel est la nature de l'interaction ?
Si elle existe ?
c) donner le sens d'inclinaison de la tige $OM$
d) Donner l'expression de l'intensité du champ magnétique $\overrightarrow{B_{2}}.$
Exercice 2
Un fil conducteur en cuivre $OA$ rigide et homogène, de masse $m$, de longueur $l$, est suspendu par son extrémité supérieure en $O$ à un axe fixe $\Delta$, autour duquel il peut tourner sans frottement ; sa partie inférieure plonge dans une cuve contenant du mercure lui permettant de faire partie d'un circuit électrique comprenant un rhéostat et un générateur de tension continue $G$ qui plonge dans une région où règne un champ magnétique uniforme $B$ orthogonal au plan de la figure.
En fermant l'interrupteur $K$, un courant électrique d'intensité $I$ traverse le fil $OA$ et celui-ci prend la position indiquée par le schéma ci-dessous.

1) Représenter les forces exercées sur le fil.
2) Indiquer sur le schéma le sens du courant électrique.
3) En appliquant la condition d'équilibre à la tige,
Calculer l'angle $\alpha$ que fait le fil conducteur avec la verticale.
On donne $I=5A$,
$l=25\,cm$,
$m=8\,g$ et $\|B\|=0.05T.$
Exercice 3
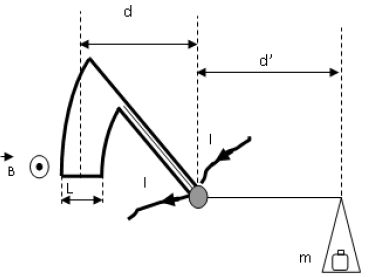
On considère le dispositif suivant appelé : Balance de Cotton.
Les extrémités du fil conducteur sont reliées à un générateur de tension continue débitant un courant d'intensité $I.$
On ajoute sur le plateau une masse marquée $m$ pour équilibrer la balance.
Ainsi on remplit le tableau de valeurs suivant :
$$\begin{array}{|c|c|c|c|c|c|c|} \hline I(A)&0&2&4&6&8&10\\ \hline m(g)&0&0.4&0.8&1.2&1.6&2\\ \hline \end{array}$$
1) Tracer la courbe $m=f(I).$
2) En appliquant la condition d'équilibre à la balance, établir la relation théorique $m=f(I).$
3) Déduire la valeur du champ magnétique $\|B\|.$
On donne $L=2\,cm$ et $d'=5/4\cdot d$
4) Peut-on accrocher une masse $m=2.45\,g$, sachant que le fil conducteur de la balance ne peut supporter qu'une intensité de $12\,A$, pour que la balance soit en équilibre.
Exercice 4
On néglige les forces de frottement et le champ magnétique terrestre.
Deux barres conductrices sont disposées parallèlement suivant la ligne de plus grande pente d'un plan incliné d'un angle $\theta$ sur l'horizontale.
Elles sont distantes de $L$ ; leurs extrémités supérieures sont reliées entre elles par un générateur $G$ et par un interrupteur $K.$
Une barre $MN$ conductrice est posée perpendiculairement sur les deux barres précédentes.
Le contact électrique se fait en $M$ et $N.$
On crée dans la région où se trouve la barre $MN$ un champ magnétique uniforme $\overrightarrow{B}$ perpendiculaire au plan des rails.
On ferme $K.$
Un courant d'intensité $I$ circule dans le montage.
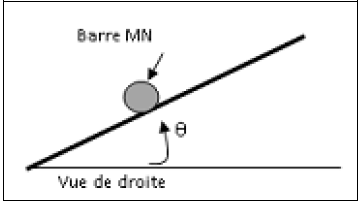
1) Représenter les forces exercées sur la barre $MN$ pour qu'elle puisse être en équilibre (on peut utiliser la vue de droite).
Déduire le sens de $\overrightarrow{B}$
2) La barre $MN$ a une masse $m=10\,g$ et pour qu'elle soit en équilibre il faut que l'intensité du courant soit égale à $I_{1}=10\,A.$
a) Établir la condition d'équilibre de la barre $MN$
b) Exprimer la norme de $\overrightarrow{B}$ en fonction de $I_{1}$, $L$, $m$, $g$ et $\theta$ pour que la barre reste en équilibre.
Montrer que $\|\overrightarrow{B}\|=68\,mT.$
On donne :
$\theta=20^{\circ}$ ;
$g=10\,N/kg$ et $L=0.05\,m.$
L'intensité du courant est $I_{2}=15\,A$ et on garde le champ magnétique $\overrightarrow{B}$ précédent, on place sous la barre $MN$ un ressort à spires non jointives, de raideur $k$ de masse négligeable dont la direction est celle de la plus grande pente du plan incliné (voir figure ci-dessous).
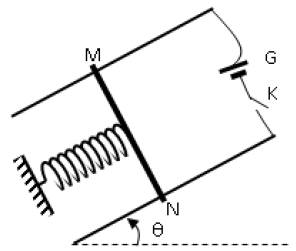
Lorsque l'interrupteur $K$ est ouvert la barre $MN$ est en équilibre.
On ferme l'interrupteur $K$, la barre $MN$ prend une nouvelle position d'équilibre $M'N'$ tel que le ressort soit allongé de $\Delta\;l=3.36\,mm.$
a) Représenter les forces exercées sur la barre $MN$ (on peut utiliser la vue de droite).
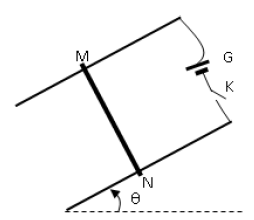
b) Établir la condition d'équilibre de la barre.
Déduire la valeur de la constante de raideur $k$ du ressort.
Exercice 5
On donne $\|\overrightarrow{g}\|=10\,N\cdot Kg^{-1}$
On considère le dispositif représenté sur la figure 1 :
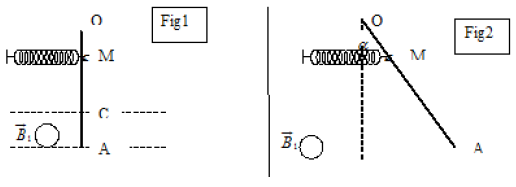
$OA$ est une tige conductrice de longueur $OA=L=40\,cm$ de masse $m=3\,g$, mobile autour d'une axe horizontal passant par son extrémité $O.$
L'autre extrémité $A$ est reliée à un fil souple conducteur ne gênant nullement le mouvement possible de la tige.
Cette tige est soumise à l'action d'un champ magnétique uniforme $\overrightarrow{B_{1}}$ perpendiculaire au plan de la figure de valeur $\|\overrightarrow{B_{1}}\|=0.1\,T.$
Ce champ $\|\overrightarrow{B_{1}}\|$ règne dans une région limitée par $AC=l=10\,cm.$
Au point $M$ de la tige tel que $OM=10\,cm$ est attaché un ressort horizontal ; isolant de raideur $K=23\,N\cdot m^{-1}.$
Lorsque la tige est traversée par un courant d'intensité $I_{1}=10\,A$ ; elle dévie d'un angle $\alpha=8^{\circ}$ et se stabilise dans une nouvelle position d'équilibre (voir figure 2).
On suppose que la déviation $\alpha$ est faible de façon que la partie plongée dans le champ reste sensiblement la même et le ressort reste horizontal et allongé de $\Delta\;l.$
1) a) Indiquer le sens du courant traversant la tige.
b) Donner les caractéristiques de la force de la place exercée sur la tige.
2) a) Faire le bilan des forces exercées sur la tige lorsqu'elle parcourue par le courant $I_{1}.$
b) En appliquant le théorème des moments à la tige, déterminer l'allongement du ressort $\Delta\;l.$
3) On enlève le ressort et on superpose au champ $\overrightarrow{B_{1}}$ un autre champ $\overrightarrow{B_{2}}$ perpendiculaire au plan de la figure et opposé à $\overrightarrow{B_{1}}.$
Le champ $\overrightarrow{B_{2}}$ règne dans une région de façon que la tige soit totalement plongée dans cette région.
La tige est toujours parcourue par le même courant $I_{1}=10\,A$ et dans le même sens que 2) ;
La déviation de la tige par rapport à la verticale est alors $\theta=4^{\circ}$ ;
a) Faire le bilan des forces exercées sur la tige.
b) Déterminer la valeur du champ magnétique $\overrightarrow{B_{2}}.$
4) Dans cette question la tige $OA$ est isolée du montage précèdent ; elle est liée au bras d'une balance dont les deux bras sont isolants et égaux.
La tige est maintenue horizontale dans un plan perpendiculaire au plan de la figure 3 et elle est parcourue par un courant d'intensité $I_{3}$
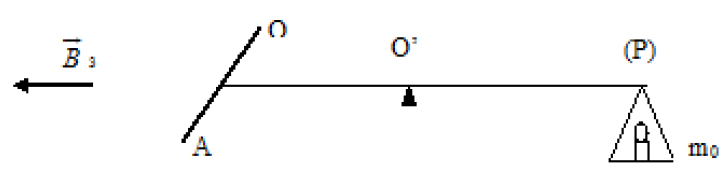
Ce courant est amené par deux fils souples et de masse négligeable.
La tige est complètement plongée dans un champ $\overrightarrow{B_{3}}$ horizontal et contenu dans le plan de la figure tel que $\overrightarrow{B_{3}}=5\cdot 10^{-2}T.$
En l'absence de courant $I_{3}$ ; la tige $OA$ et le fléau sont en équilibre horizontaux.
Lorsque la tige est traversée par $I_{3}$ ; il faut placer une masse $m_{0}=4\,g$ sur le plateau $P$ pour rétablir l'équilibre horizontal.
a) Déduire de ces expériences les caractéristiques de la force de Laplace.
b) Préciser le sens du courant $I_{3}$ et calculer sa valeur.
Exercice 6
On considère le dispositif de la figure 1 qui est constitué de :

$-\ $ deux rails en cuivre $AD$ et $CE$ horizontaux.
$-\ $ Une tige $(T)$ en cuivre, pouvant glisser sans frottement sur les rails.
Sa partie centrale de longueur $l=10\,cm$ baigne dans un champ magnétique $\overrightarrow{B}$ vertical.
Un fil $(f)$ inextensible, de masse négligeable, attaché par l'une de ses extrémités au milieu de la tige $(T)$ et par l'autre extrémité à un ressort de masse négligeable et de raideur $k=10\,N\cdot m^{-1}.$
L'autre extrémité du ressort étant fixe.
Une poulie $(P)$ de masse négligeable pouvant tourner sans frottement autour de son axe.
$-\ $ Un rhéostat $Rh$ permettant la variation de l'intensité $I$ de courant dans le circuit.
1) a) Représenter sur un schéma clair les forces qui s'exercent sur la tige $(T).$
On rappelle que la tension du ressort est de la forme $T=k\cdot x$
b) A quelle force est du l'allongement du ressort ?
Préciser le sens et la direction de cette force.
c) Indiquer, en le justifiant le pôle nord et le pôle sud de l'aimant.
2) A l'aide du rhéostat on fait varier l'intensité $I$ du courant dans le circuit et on note l'allongement $x$ du ressort lorsque la tige $(T)$ est en équilibre.
Les résultats des mesures ont permis de tracer la courbe : $I=f(x)$ de la figure 2
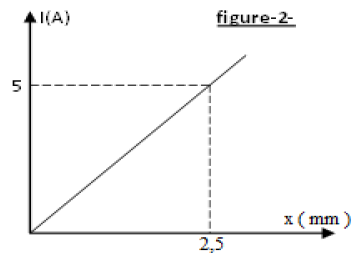
a) Montrer que l'équation de la courbe est de la forme : $I=a\,x.$
b) Donner la signification mathématique et la valeur de $a.$
c Écrire la relation qui lie $B$, $I$, $k$, $x$ et $L.$
d) En déduire l'intensité $B$ du champ magnétique qui règne entre les branches de l'aimant en $U.$
3) On détache la barre, on inverse le sens du courant dans le circuit, dont l'intensité est fixée à $I=1A.$
Pour maintenir la tige $(T)$ en équilibre sur les rails, on incline le plan horizontal supportant le dispositif de $\alpha=15^{\circ}.$ (Figure 3)

a) Représenter les forces qui s'exercent sur la tige.
b) Montrer que la masse $m$ de la tige $(T)$ est donnée par l'expression :
$m=\dfrac{IBL}{g\sin\alpha}$,
c) Calculer sa valeur.
On donne : $g=9.8\,N\cdot Kg^{-1}$

Commentaires
Bocar (non vérifié)
lun, 02/10/2020 - 11:09
Permalien
Pro physique
mek (non vérifié)
mer, 01/20/2021 - 15:56
Permalien
prof
so (non vérifié)
jeu, 01/21/2021 - 22:25
Permalien
correction svp
physique (non vérifié)
jeu, 01/21/2021 - 22:46
Permalien
correction
Fatou fall (non vérifié)
mar, 05/04/2021 - 00:27
Permalien
J ai besoin de la correction
Kpédio ayaovi (non vérifié)
dim, 05/30/2021 - 13:48
Permalien
Correction
Kpédio ayaovi (non vérifié)
dim, 05/30/2021 - 13:48
Permalien
Correction
Ravys (non vérifié)
sam, 01/22/2022 - 20:15
Permalien
Demandé
OUOKOSHI Chris chail (non vérifié)
jeu, 04/14/2022 - 16:37
Permalien
Correction
Ait non (non vérifié)
dim, 05/22/2022 - 19:28
Permalien
Ex 2
Keita Balamoussa (non vérifié)
mar, 02/28/2023 - 12:59
Permalien
Je veux les corrections des
Abdelouaheb (non vérifié)
sam, 05/18/2024 - 00:02
Permalien
tres interessant
Ajouter un commentaire