Les triangles - 5e

Classe:

Cinquième

I. Définition et construction

Un triangle est une figure géométrique qui a trois côtés donc, trois sommets et trois angles.

Construisons un triangle quelconque

$ABC$ tel que :

$AB=6\;cm\;;\quad BC=3\;cm\;;\quad\text{et}\quad AC=5\;cm$

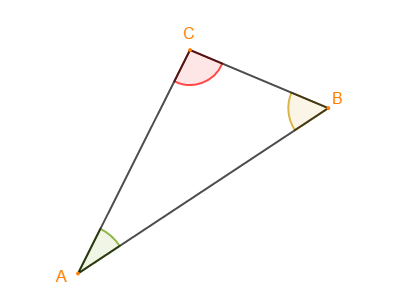
$\centerdot\ \ [AB]\;,\ [BC]\;,\ [AC]$ sont les côtés du triangle.

$\centerdot\ \ A\;,\ B\;,\ C$ sont les sommets du triangle

$\centerdot\ \ \widehat{BAC}\;,\ \widehat{CBA}\;,\ \widehat{ACB}$ sont les angles

Application

Construis un triangle

$MNS$ tel que :

$MN=6\;cm\;;\quad \widehat{MNS}=63^{\circ}\;;\quad\text{et}\quad \widehat{SMN}=47^{\circ}$

Déterminez

$\ \widehat{MSN}$

Solution

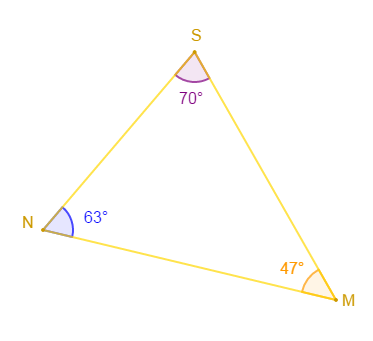
On sait que la somme des mesures des angles d'un triangle est toujours égale à

$180^{\circ}.$

Donc,

$\widehat{MSN}+\widehat{MNS}+\widehat{SMN}=180^{\circ}$

Ainsi,

$\begin{array}{rcl}\widehat{MSN}&=&180^{\circ}-(\widehat{MNS}+\widehat{SMN})\\\\&=&180^{\circ}-(63^{\circ}+47^{\circ})\\\\&=&180^{\circ}-110^{\circ}\\\\&=&70^{\circ}\end{array}$

D'où,

$\boxed{\widehat{MSN}=70^{\circ}}$

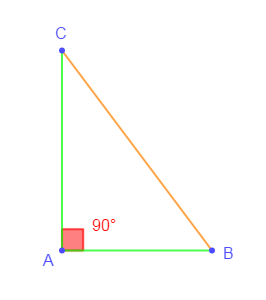
$\centerdot\ \$ Triangle rectangle

Un triangle rectangle est un triangle possédant un angle de

$90^{\circ}.$

Exemple

Construisons un triangle

$ABC$ rectangle en

$A$ tel que :

$AB=3\;cm\ \text{ et }\ AC=4\;cm$

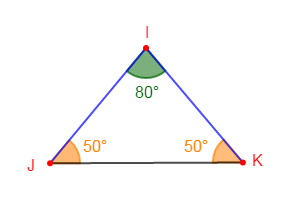
$\centerdot\ \$ Triangle isocèle

Un triangle isocèle est un triangle ayant deux côtés de même longueur.

Exemple

Construisons un triangle

$IJK$ isocèle en

$I$ tel que :

$IJ=IK=3\;cm\ \text{ et }\ \widehat{I}=80^{\circ}$

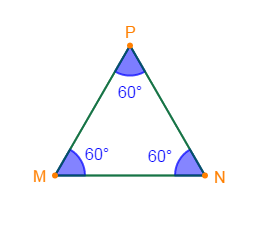
$\centerdot\ \$ Triangle équilatéral

Un triangle équilatéral est un triangle dont les trois côtés sont de même longueur.

Exemple

Construisons un triangle équilatéral

$MNP$ tel que :

$MN=3\;cm$

II. Propriétés

$-\ \$ Pour tout triangle, la somme de ses angles fait

$180^{\circ}.$

D'après l'application précédente, on a :

$mes(\widehat{NMS})+mes(\widehat{SNM})+mes(\widehat{MSN})=180^{\circ}$

c'est-à-dire ;

$47^{\circ}+63^{\circ}+70^{\circ}=180^{\circ}$

$-\ \$ Dans un triangle rectangle, les angles aigus sont complémentaires

$-\ \$ Dans un triangle isocèle, les angles adjacents à la base sont de même mesure.

$-\ \$ Un triangle équilatéral a trois angles internes qui ont la même mesure de

$60^{\circ}$

III. Les droites remarquables dans un triangle

III.1. La médiatrice

La médiatrice d'un côté d'un triangle, c'est la droite passant par le milieu de celui-ci et qui lui est perpendiculaire.

Remarque

Tout triangle possède trois médiatrices qui se coupent en un même point appelé centre du cercle circonscrit à ce triangle.

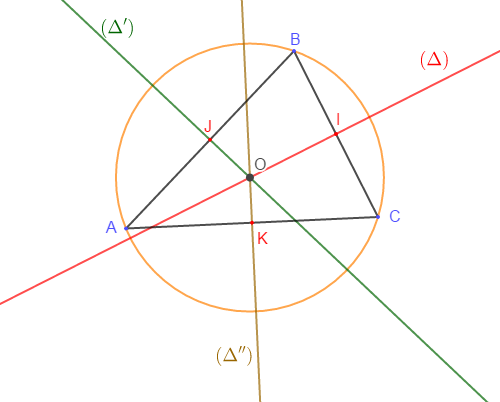
$O$ est le centre du cercle circonscrit

III.2. La bissectrice

Dans un triangle, on appelle bissectrice d'un angle toute droite passant par le sommet de celui-ci et qui le partage en deux angles de même mesure.

Remarque

Tout triangle possède trois bissectrices qui sont concourantes en un même point appelé centre du cercle inscrit dans ce triangle.

Application

1) Construis un triangle

$ABC$ tel que :

$AB=5\;cm\;;\quad BC=4\;cm\;;\quad\text{et}\quad AC=6\;cm$

2) Tracez les bissectrices des angles

$\widehat{A}\;,\ \widehat{B}\;,\ \widehat{C}$ se coupant en

$I.$

3) Comment appelle-t-on le point

$I.$

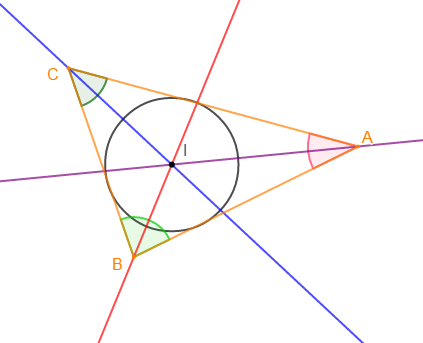
$I$ est le centre du cercle inscrit

III.3. La hauteur

Dans un triangle, on appelle hauteur la droite issue d'un sommet de ce triangle et qui est perpendiculaire au côté opposé de ce sommet.

Remarque

Tout triangle possède trois hauteurs qui sont concourantes en un même point appelé orthocentre.

Exemple

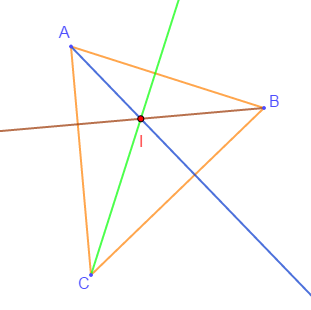
Application

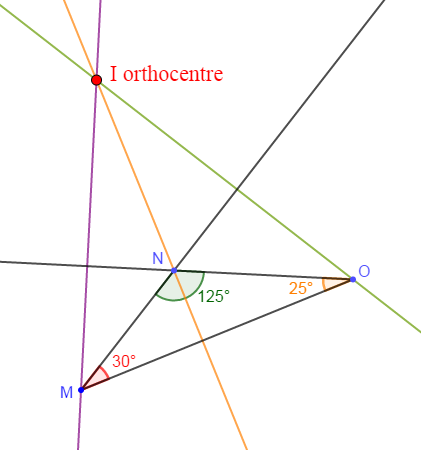
1) Construire un triangle

$MNO$ tel que :

$\widehat{MNO}=125^{\circ}\;;\quad \widehat{MON}=25^{\circ}\;;\quad\text{et}\quad \widehat{NMO}=30^{\circ}$

2) Préciser l'orthocentre

$I$

Solution

Remarque

$-\ \$ L'orthocentre peut ne pas être à l'intérieur du triangle

$-\ \$ Si le triangle

$ABC$ est rectangle en

$A$ alors :

$\cdot\$ l'orthocentre est le point

$A$

$\cdot\$ le côté le plus long,

$BC$ est appelé hypoténuse

$\cdot\$ le centre du cercle circonscrit est le milieu de l'hypoténuse

III.4. La médiane

Dans un triangle, une médiane est une droite passant par un sommet et par le milieu du côté opposé à ce sommet.

Remarque

$-\ \$ Tout triangle possède trois médianes qui sont concourantes en un même point appelé centre de gravité.

$-\ \$ Le centre de gravité d'un triangle est situé aux deux tiers de chaque médiane à partir du sommet.

Application

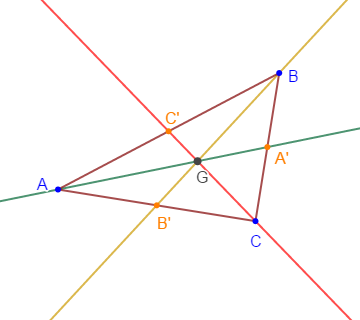
1) Construire un triangle

$ABC$ tel que :

$AB=5\;cm\;;\quad BC=3\;cm\;;\quad\text{et}\quad AC=4\;cm$

2) Tracer les trois médianes puis placer le centre de gravité

$G$ de ce triangle

Solution

Auteur:

Mamadou Siradji Dia

Commentaires

Anonyme (non vérifié)

lun, 11/22/2021 - 13:12

Permalien

Pdf

répondre

Bernadette Beya (non vérifié)

mer, 03/02/2022 - 18:04

Permalien

C'est pour mon fils

C'est très bien ça

répondre

Anonyme (non vérifié)

lun, 11/22/2021 - 13:12

Permalien

Pdf

répondre

Anonyme (non vérifié)

mer, 01/19/2022 - 07:45

Permalien

c est tres bien fait!

répondre

Ndeye fatou ndiaye (non vérifié)

jeu, 04/28/2022 - 23:58

Permalien

Merci beaucoup c intéressant

répondre

Seynabou kama (non vérifié)

lun, 05/16/2022 - 21:58

Permalien

Genial

répondre

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Les triangles - 5e

Formulaire de recherche

I. Définition et construction

Application

Solution

⋅ \centerdot\ \ Triangle rectangle

⋅ \centerdot\ \ Triangle isocèle

⋅ \centerdot\ \ Triangle équilatéral

II. Propriétés

III. Les droites remarquables dans un triangle

III.1. La médiatrice

III.2. La bissectrice

Application

III.3. La hauteur

Application

Solution

III.4. La médiane

Application

Solution

Commentaires

Pdf

C'est pour mon fils

Pdf

c est tres bien fait!

Merci beaucoup c intéressant

Genial

Ajouter un commentaire

Plain text

$\centerdot\ \$ Triangle rectangle

$\centerdot\ \$ Triangle isocèle

$\centerdot\ \$ Triangle équilatéral