Angle inscrit - Angle au centre - 3e
Classe:
Troisième
I. Rappels
$\centerdot\ \ $ Angles alternes internes
On appelle angles alternes-internes deux angles situés de part et d'autre d'une sécante à deux droites parallèles et à l'intérieur de la région délimitée par les deux parallèles.
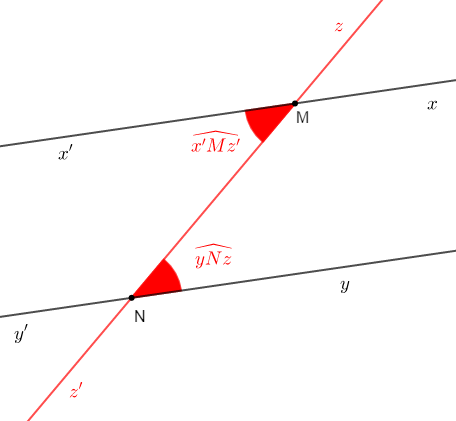
$\widehat{x'Mz'}$ et $\widehat{yNz}$ sont deux angles alternes-internes.
Ainsi, $\widehat{x'Mz'}=\widehat{yNz}$
$\centerdot\ \ $ Angles supplémentaires
Deux angles sont dits angles supplémentaires si la somme de leur mesure est égale à la mesure d'un angle plat.
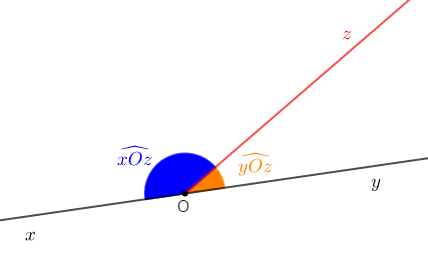
Ainsi, $\widehat{xOz}+\widehat{yOz}$ est égale à $180^{\circ}.$
Elles sont deux angles supplémentaires.
$\centerdot\ \ $ Quadrilatère convexe
On appelle quadrilatère convexe, un quadrilatère dont les diagonales sont totalement à l'intérieur de la surface délimitée par le quadrilatère.
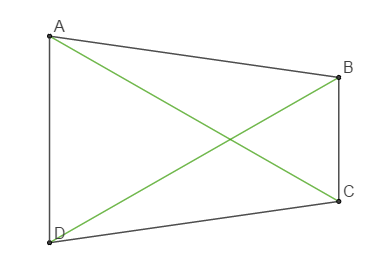
$ABCD$ est un quadrilatère convexe
$\centerdot\ \ $ Le cercle
On appelle cercle de centre $O$ et de rayon $r$ noté $\mathcal{C}(O\;;\ r)$, l'ensemble des points d'un plan équidistants du point $O$ de ce plan.
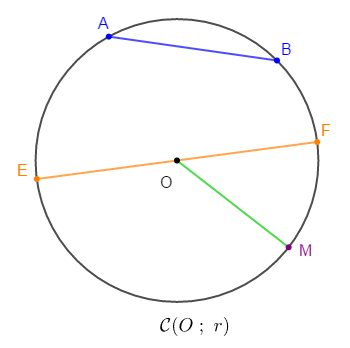
$\centerdot\ \ $ Corde
C'est un segment qui a pour extrémité deux points d'un cercle. $[AB]$ est une corde de $\mathcal{C}.$
Si la corde contient le point centre du cercle alors elle est appelée diamètre.
$\centerdot\ \ $ Arc de cercle
La corde $[AB]$ divise le cercle en deux parties appelées arcs de cercle : le petit arc noté $\overset{\displaystyle\frown}{AB}$ est l'arc de cercle saillant et grand arc noté $\overset{\displaystyle\smile}{AB}$ est l'arc de cercle rentrant.
II. Angles inscrits
On appelle angle inscrit dans un cercle, un angle dont :
$-\ \ $ le sommet est un point du cercle
$-\ \ $ ses côtés recoupent le cercle
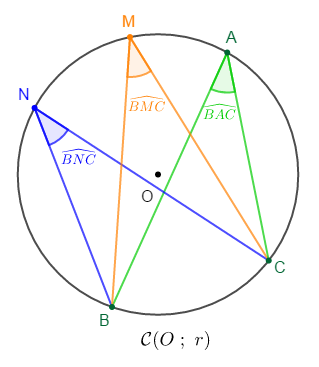
$\widehat{BAC}\;,\ \widehat{BMC}$ et $\widehat{BNC}$ sont des angles inscrits dans $\mathcal{C}$
Remarque : angle inscrit limite
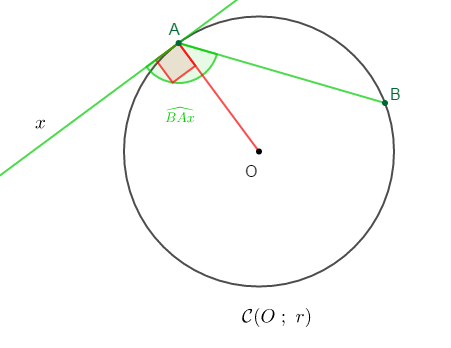
$\widehat{BAx}$ est un angle inscrit limite.
III. Angle au centre
On appelle angle au centre, un angle dont le sommet est le centre d'un cercle.
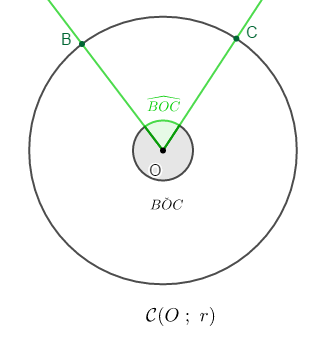
$\widehat{BOC}$ et $B\check{O}C$ sont des angles au centre dans $\mathcal{C}$
IV. Angle inscrit et angle au centre associé (correspondant)
IV.1 Arc intercepté
On appelle arc intercepté par un angle inscrit (ou un angle au centre) dans un cercle, l'arc de cercle contenu dans le secteur angulaire défini par l'angle.
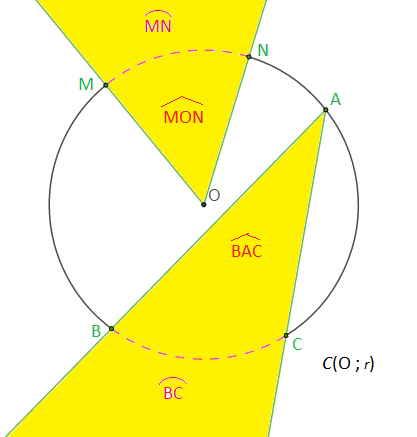
$\overset{\displaystyle\frown}{BC}$ et $\overset{\displaystyle\frown}{MN}$ sont les arcs interceptés respectivement par $\widehat{BAC}$ et $\widehat{MON}$
IV.2 Définition
On appelle angle inscrit et angle au centre associé dans un cercle, un angle inscrit et un angle au centre du cercle interceptant le même arc.
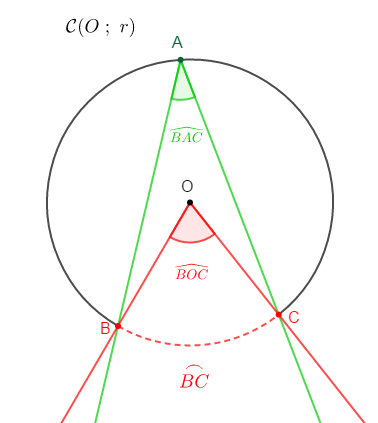
$\widehat{BAC}$ et $\widehat{BOC}$ sont dits angle inscrit et angle au centre associé.
IV.3 Relation entre un angle inscrit et un angle au centre associé
a) cas où un côté de l'angle inscrit est diamètre
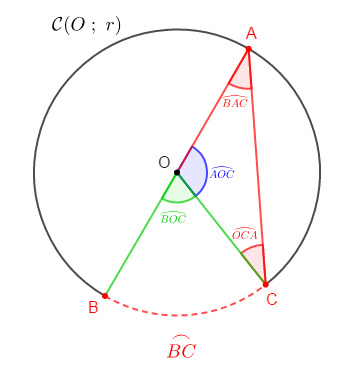
On a $OAC$ un triangle isocèle en $O$ alors, $\widehat{BAC}=\widehat{OCA}$
et comme $\widehat{BAC}+\widehat{OCA}+\widehat{AOC}=180^{\circ}$
$\widehat{AOC}+\widehat{BOC}=180^{\circ}$
donc, $\widehat{BAC}+\widehat{BAC}+\widehat{AOC}=\widehat{AOC}+\widehat{BOC}$
D'où, $$\boxed{2\widehat{BAC}=\widehat{BOC}}$$
b) cas où le point $O$ est à l'intérieur du secteur angulaire
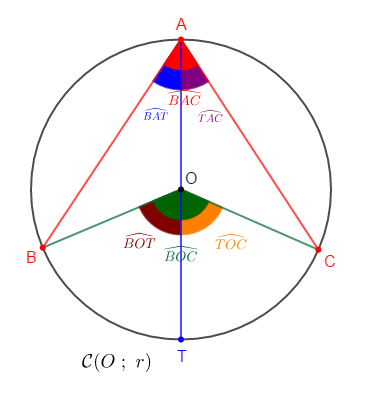
Soit $T\in\;\mathcal{C}(O\;;\ r)$ tel que $[AT]$ diamètre de $\mathcal{C}.$
On aura : $2\widehat{BAT}=\widehat{BOT}$ et $2\widehat{TAC}=\widehat{TOC}$
Donc, $2(\widehat{BAT}+\widehat{TAC})=\widehat{BOT}+\widehat{TOC}$
Or, $\widehat{BAT}+\widehat{TAC}=\widehat{BAC}$ et $\widehat{BOT}+\widehat{TOC}=\widehat{BOC}$
D'où, $$\boxed{2\widehat{BAC}=\widehat{BOC}}$$
c) cas où le point $O$ est extérieur au secteur angulaire
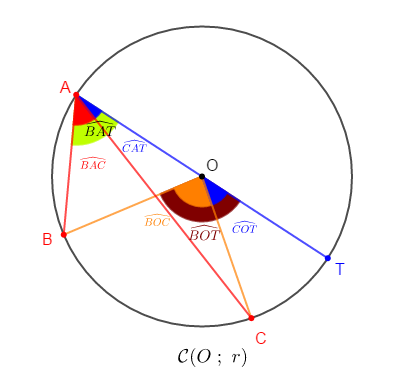
Soit $T\in\;\mathcal{C}(O\;;\ r)$ tel que $[TA]$ diamètre de $\mathcal{C}.$
On aura : $2\widehat{BAT}=\widehat{BOT}$ et $2\widehat{CAT}=\widehat{COT}$
Alors, $2\widehat{BAT}-2\widehat{CAT}=\widehat{BOT}-\widehat{COT}$
Donc, $2(\widehat{BAT}-\widehat{CAT})=\widehat{BOT}-\widehat{COT}$
Or, $\widehat{BAT}-\widehat{CAT}=\widehat{BAC}$ et $\widehat{BOT}-\widehat{COT}=\widehat{BOC}$
D'où, $$\boxed{2\widehat{BAC}=\widehat{BOC}}$$
d) cas de l'angle inscrit limite
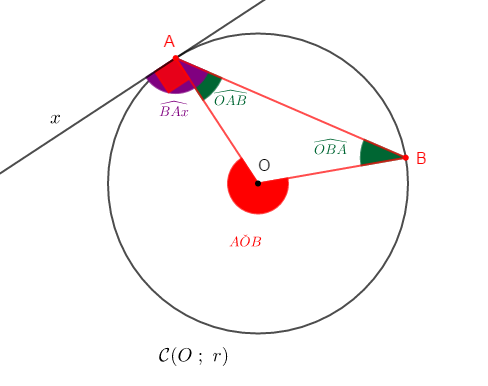
On a : $OAB$ un triangle isocèle en $O$ alors, $\widehat{OAB}=\widehat{OBA}$
et comme $\widehat{AOB}+\widehat{OAB}+\widehat{OBA}=180^{\circ}$
donc, $\widehat{AOB}+2\widehat{OAB}=180^{\circ}$
Ainsi, $\widehat{AOB}=180^{\circ}-2\widehat{OAB}$
De plus on a : $\widehat{AOB}=360^{\circ}-A\check{O}B$
Aar suite, $180^{\circ}-2\widehat{OAB}=360^{\circ}-A\check{O}B$
$A\check{O}B=180^{\circ}+2\widehat{OAB}$
$A\check{O}B=2(90^{\circ}+\widehat{OAB})$
Or, $90^{\circ}+\widehat{OAB}=\widehat{BAx}$
D'où, $$\boxed{A\check{O}B=2\widehat{BAx}}$$
$\centerdot\ \ $ Énoncé du théorème
Dans un cercle, le double de l'angle inscrit est égal à la mesure de son angle au centre associé. Si $\widehat{BAC}$ un angle inscrit dans un cercle $\mathcal{C}$ et $\widehat{BOC}$ son angle au centre associé, alors $$2\widehat{BAC}=\widehat{BOC}$$
V. Angles inscrits interceptant le même arc dans un cercle
Soient $\widehat{BAC}\;,\ \widehat{BMC}$ et $\widehat{BNC}$ trois angles inscrits dans un cercle $\mathcal{C}(O\;;\ r)$
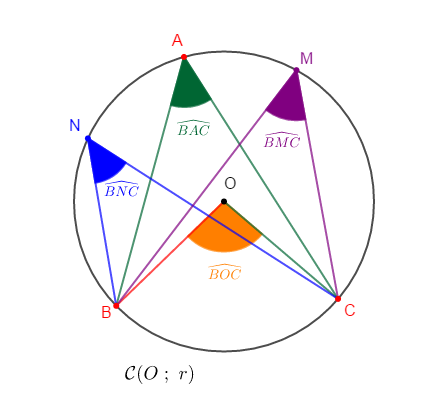
On a : $\widehat{BAC}\;,\ \widehat{BMC}$ et $\widehat{BNC}$ trois angles inscrits dans un cercle $\mathcal{C}$ ayant pour angle au centre associé $\widehat{BOC}.$
Alors, $2\widehat{BAC}=\widehat{BOC}\;,\ 2\widehat{BMC}=\widehat{BOC}$ et $2\widehat{BNC}=\widehat{BOC}$
Donc, $2\widehat{BAC}=2\widehat{BMC}=2\widehat{BNC}$
D'où, $$\boxed{\widehat{BAC}=\widehat{BMC}=\widehat{BNC}}$$
$\centerdot\ \ $ Énoncé du théorème
Dans un cercle, deux angles inscrits interceptant le même arc ont la même mesure.
Si $\widehat{BAC}$ et $\widehat{BMC}$ deux angles inscrits dans $\mathcal{C}$, alors $$\widehat{BAC}=\widehat{BMC}$$
VI. Théorèmes complémentaires
VI.1 Triangle inscrit dans un cercle ayant un côté comme diamètre
Soit $ABC$ un triangle inscrit dans un cercle $\mathcal{C}(O\;;\ r)$ tel que $[BC]$ diamètre de $\mathcal{C}.$
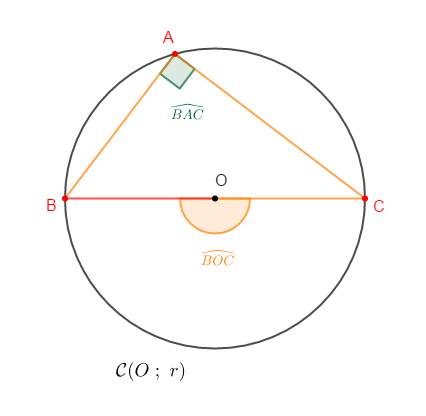
On a $\widehat{BAC}$ un angle inscrit dans $\mathcal{C}$ ayant pour angle au centre associé $\widehat{BOC}.$
Alors, $2\widehat{BAC}=\widehat{BOC}$
et comme $\widehat{BOC}=180^{\circ}$
donc, $2\widehat{BAC}=180^{\circ}$
D'où, $$\boxed{\widehat{BAC}=90^{\circ}}$$
$\centerdot\ \ $ Énoncé du théorème
Si un triangle est inscrit dans un cercle et ayant un côté comme diamètre, alors c'est un triangle rectangle d'hypoténuse, le côté représentant le diamètre.
$$\text{Si }\;\left\lbrace\begin{array}{lll} ABC\;\text{ triangle } \\ \\ \mathcal{C}(O\;;\ r)=\mathcal{C}(ABC) \\ \\O\;\text{ est milieu de }\;[BC] \end{array}\right.\quad\text{alors, }\;ABC\;\text{ est rectangle en }\;A$$
Réciproque :
Le cercle circonscrit à un triangle rectangle a pour centre le milieu de l'hypoténuse.
$$\text{Si }\;\left\lbrace\begin{array}{lll} ABC\;\text{ triangle rectangle en }A \\ \\ \mathcal{C}(O\;;\ r)=\mathcal{C}(ABC) \end{array}\right.\quad\text{alors, }\;O\;\text{ est milieu de }\;[BC]$$
VI.2 Quadrilatère convexe inscrit dans un cercle
Soit $ABCD$ un quadrilatère convexe inscrit dans un cercle $\mathcal{C}(O\;;\ r)$
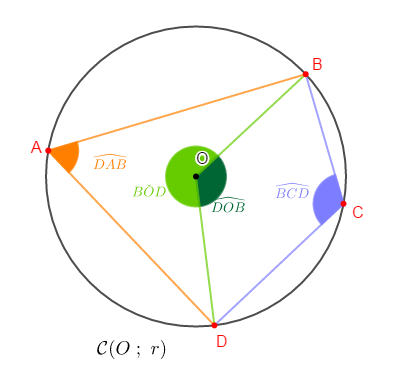
On a $\widehat{BAD}$ et $\widehat{BOD}$ respectivement angle inscrit et angle au centre associé ; alors $2\widehat{BAD}=\widehat{BOD}.$
De même, on a $\widehat{BCD}$ et $B\check{O}D$ angle inscrit et angle au centre associé respectivement ; alors $2\widehat{BCD}=B\check{O}D$
et comme $\widehat{BOD}+B\check{O}D=360^{\circ}$
donc $2\widehat{BAD}+2\widehat{BCD}=360^{\circ}$
D'où $$\boxed{\widehat{BAD}+\widehat{BCD}=180^{\circ}}$$
$\centerdot\ \ $ Énoncé du théorème
Si un quadrilatère convexe est inscriptible dans un cercle, alors les angles opposés sont supplémentaires.
$$\text{Si }\;\left\lbrace\begin{array}{lll} ABCD\;\text{ un quadrilatère convexe } \\ \\ \mathcal{C}(O\;;\ r)=\mathcal{C}(ABCD) \end{array}\right.\;\text{alors, }\;\left\lbrace\begin{array}{lll} \widehat{BAD}+\widehat{BCD}=180^{\circ} \\ \\ \widehat{ABC}+\widehat{ADC}=180^{\circ}\end{array}\right.$$
Réciproque :
Si un quadrilatère convexe a deux angles opposés supplémentaires, alors il est inscriptible dans un cercle.
$$\text{Si }\;\left\lbrace\begin{array}{lll} ABCD\;\text{ un quadrilatère convexe } \\ \\ \widehat{BAD}+\widehat{BCD}=180^{\circ}\end{array}\right.\;\text{alors, }\;\mathcal{C}(ABCD)$$
VII. Longueur d'un arc de cercle
Soient $\widehat{MON}$ et $\widehat{ROS}$ deux angles au centre de valeurs respectives $\alpha^{\circ}$ et $\theta^{\circ}$ d'un cercle ; $\ell$ et $\ell'$ les longueurs des arcs de cercle interceptés respectivement par $\widehat{MON}$ et $\widehat{ROS}$ dans le cercle.
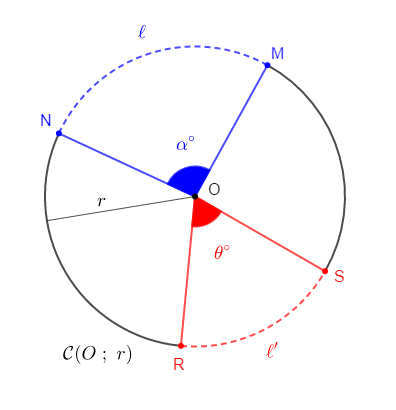
$\ell$ et $\ell'$ sont respectivement proportionnelles à $\alpha^{\circ}$ et $\theta^{\circ}.$
On aura : $\dfrac{\ell}{\ell'}=\dfrac{\alpha^{\circ}}{\theta^{\circ}}$
en posant $\theta^{o}=360^{\circ}$ ; c'est à dire $\ell'=2\pi r$ alors, $\dfrac{\ell}{2\pi r}=\dfrac{\alpha^{\circ}}{360^{\circ}}$
Donc, $$\ell=2\pi r\times\dfrac{\alpha^{\circ}}{360^{\circ}}\;\text{ ou encore }\;\ell=\pi r\times\dfrac{\alpha^{\circ}}{180^{\circ}}$$
Remarque : Angles inscrits interceptant les arcs de même longueur dans un cercle
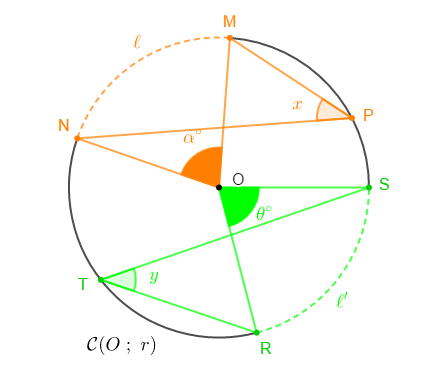
On a $\ell=2\pi r\times\dfrac{\alpha^{\circ}}{360^{\circ}}$ et $\ell'=2\pi r\times\dfrac{\theta^{\circ}}{360^{\circ}}$
En posant $\ell=\ell'$ on obtient : $2\pi r\times\dfrac{\alpha^{\circ}}{360^{\circ}}=2\pi r\times\dfrac{\theta^{\circ}}{360^{\circ}}$
Donc, $\alpha^{\circ}=\theta^{\circ}$
et comme $2x=\alpha^{\circ}$ et $2y=\theta^{\circ}$
alors, $2x=2y$
D'où, $x=y$
$\centerdot\ \ $ Énoncé du théorème
Dans un cercle, deux angles inscrits interceptant deux arcs de mêmes longueurs ont la même mesure.
Lien cours vidéo:

Commentaires
Anonyme (non vérifié)
jeu, 06/27/2019 - 21:17
Permalien
C bien c cours et merci pour
Anonyme (non vérifié)
jeu, 06/27/2019 - 21:17
Permalien
Oui t a raison
Anonyme (non vérifié)
dim, 02/16/2020 - 20:51
Permalien
qu est ce qui justifie ce que
Anonyme (non vérifié)
dim, 02/16/2020 - 20:51
Permalien
qu est ce qui justifie ce que
Ajouter un commentaire