Vous êtes ici

Application affine - Application affine par intervalle - 3e

Classe:

Troisième

I. Rappels

I.1 Nombre proportionnel

a) Définition

Les nombres réels

$x\;,\ y$ et

$z$ sont respectivement proportionnels aux réels

$a\;,\ b$ et

$c$ si, et seulement si, il existe un réel

$k$ non nul tel que :

$\boxed{\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}=k}$

Le réel

$k$ est appelé coefficient de proportionnalité.

b) Propriétés

Si les réels

$x$ et

$y$ non nuls sont respectivement proportionnels aux réels non nuls

$a$ et

$b$ , alors

$\dfrac{x}{a}=\dfrac{y}{b}.$

Application

Trouvons les réels

$x$ et

$y$ tels que

$\dfrac{x}{5}=\dfrac{y}{4}$ et

$x+y=27$

On aura

$\dfrac{x}{5}=\dfrac{y}{4}=\dfrac{x+y}{5+4}=\dfrac{27}{9}=3$

Alors,

$\dfrac{x}{5}=3$ , donc

$x=15$ et

$y=12.$

I.2 Application linéaire

a) Définition

Une application linéaire traduit une situation de proportionnalité étant donné un nombre réel

$a.$

Le procédé qui à tout

$x$ fait correspondre le réel

$y=ax$ est appelé une application linéaire de coefficient linéaire

$a.$

On notera :

$ax \curvearrowright y=ax$ .

Si on désigne par

$f\;,\ g$ ou

$h$ ce procédé on écrira :

$x\curvearrowright f(x)=ax$ .

Les applications $f\;,\ g\;,\ h$ et $m$ définies respectivement par $f(x)=2x$ , $g(x)=\dfrac{2}{3}x$ , $h(x)=\sqrt{5}x$ et $m(x)=0$ sont des applications linéaires.

b) Propriétés

Soit

$f$ une application linéaire définie par

$f(x)=ax$ ;

$\centerdot\ \ f(x_{1})+f(x_{2})=f(x_{1}+x_{2})$

Exemple :

Soit

$f$ une application linéaire telle que

$f(3)=6$ et

$f(5)=10.$

Calculons

$f(8)$ . On a

$8=5+3$ alors

$f(8)=f(5)+f(3)=10+6=16.$

$\centerdot\ \ f(k.x_{1})=k.f(x_{1})$

Exemple :

Soit

$f$ une application linéaire telle que

$f(6)=2.$

Calculons

$f(30)$ . On a

$30=5\times 6$

Alors,

$f(30)=f(5\times 6)=5.f(6)=5\times 2=10.$

c) Sens de variation

Soit une application linéaire définie par

$f(x)=ax$

$\centerdot\ \$ Si

$a>0$ alors l'application linéaire

$f$ est croissante

$(\nearrow)$ ; c'est à dire si

$x_{1}<x_{2}$ alors

$f(x_{1})<f(x_{2}).$

Exemple :

L'application linéaire

$f$ définie par

$f(x)=\dfrac{2}{3}x$ est une application linéaire croissante.

$\centerdot\ \$ Si

$a=0$ l'application linéaire est dite constante ; c'est à dire si

$x_{1}<x_{2}$ alors

$f(x_{1})=f(x_{2}).$

$\centerdot\ \$ Si

$a<0$ l'application linéaire

$f$ est dite décroissante

$(\searrow)$ ; c'est à dire si

$x_{1}<x_{2}$ alors

$f(x_{1})>f(x_{2}).$

Exemple :

L'application

$f$ définie par

$f(x)=-5x$ est une application linéaire décroissante.

d) Représentation graphique

Soit

$f$ une application linéaire définie par

$f(x)=ax$ .

Représenter graphiquement l'application linéaire

$f$ , c'est représenter la droite

$(\Delta)\ :\ y=ax$ passant par le point

$O$ origine du repère et par un autre point à déterminer.

Exemple :

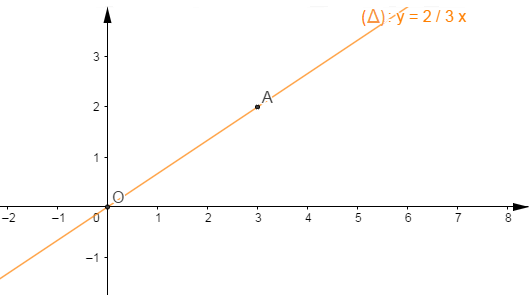
Représentons graphiquement l'application linéaire

$f$ définie par

$fx)=\dfrac{2}{3}x.$

Représenter graphiquement

$f$ ; c'est représenter la droite

$(\Delta)\ :\ y=\dfrac{2}{3}x$ passant par le point

$O$ origine du repère et par un point

$A$ dont les cordonnées vérifient l'équation de la droite

$(\Delta).$

Donc, si $x_{A}=3$ alors, en remplaçant dans l'équation de la droite $(\Delta)$ on trouve $y_{A}=2.$ D'où,

$\begin{array}{|c|c|c|}\hline & O & A \\ \hline x & 0 & 3 \\ \hline y & 0 & 2 \\ \hline\end{array}$

II. Application affine

II.1 Définition

Étant donné deux réels

$a$ et

$b$ , le procédé qui à tout réel

$x$ fait correspondre le réel

$y=ax+b$ est appelé une application affine de coefficient directeur

$a$ et d'ordonnée à l'origine

$b.$

On notera :

$x\curvearrowright y=ax+b$ .

Si on désigne par

$f\;,\ g\;,\ h$ ou

$m$ ce procédé, on écrira :

$x\curvearrowright f(x)=ax+b.$

Exemple :

Les applications

$f\;,\ g\;,\ h$ et

$p$ définies respectivement par

$f(x)=3x+5$ ,

$g(x)=\sqrt{5}$ ,

$h(x)=\dfrac{3}{4}$ et

$p(x)=\left(\dfrac{\sqrt{3}+1}{2}\right)x+1$ sont des application affines.

Remarques :

Toute application linéaire est une application affine.

II.2 Application linéaire associée

On appelle application linéaire associée à une application affine

$f$ définie par

$f(x)=ax+b$ ; l'application linéaire

$f$ définie par

$f(x)=ax.$

Exemple :

Les applications

$f$ et

$g$ définies respectivement par

$f(x)=\dfrac{3}{4}x+5$ et

$g(x)=-7$ ont pour applications associées respectives

$f_{1}$ et

$g_{1}$ définies respectivement par

$f_{1}(x)=\dfrac{3}{4}x$ et

$g_{1}(x)=0.$

II.3 Sens de variation - déterminant du coefficient directeur

Le sens de variation d'une application affine est donnée par le sens de variation de son application linéaire associée (voir sens de variation d'une application linéaire).

Exemple :

Les applications affines

$f\;,\ g$ et

$h$ définies respectivement par

$f(x)=3x+5$ ,

$g(x)=7$ et

$h(x)=-2x+4$ sont respectivement croissante, constante et décroissante.

Soit

$f$ une application affine définie par

$f(x)=ax+b$ ,

$x_{1}$ et

$x_{2}$ deux réels différents.

On a

$f(x_{1})=ax_{1}+b$ et

$f(x_{2})=ax_{2}+b$

Alors,

$f(x_{1})-f(x_{2})=(ax_{1}+b)-(ax_{2}+b)$

Donc,

$f(x_{1})-f(x_{2})=a(x_{1}-x_{2})$

D'où,

$\boxed{a=\dfrac{f(x_{1})-f(x_{2})}{x_{1}-x_{2}}}$

Application :

Détermination d'une application affine

Soit

$f$ une application affine telle que

$f(5)=-13$ et

$f(-2)=8$ .

Déterminons l'application affine

$f$ .

On a

$f(x)=ax+b$ , or

$f(5)=-13$ et

$f(-2)=8$ .

Alors,

$a=\dfrac{f(-2)-f(5)}{(-2)-(5)}=\dfrac{(8)-(-13)}{-2-5}=-3$

Donc,

$f(x)=-3x+b$ , et comme

$f(5)=-3(5)+b$ et

$f(5)=-13$

Par suite,

$-15+b=-13$

Ainsi,

$b=2$

D'où,

$f(x)=-3x+2$

II.4 Représentation graphique

Représenter graphiquement une application affine

$f$ définie par

$f(x)=ax+b$ ; c'est représenter la droite

$(\Delta)$ d'équation

$y=ax+b$ passant par deux points à déterminer.

Exemple :

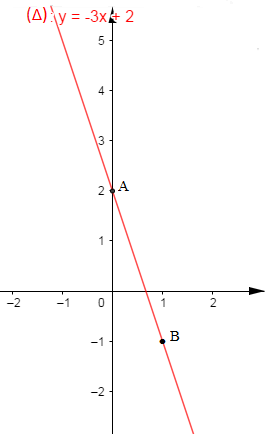
Représenter graphiquement l'application affine

$f$ définie par

$f(x)=-3x+2.$

Représenter graphiquement

$f$ c'est représenter la droite

$(\Delta)\ :\ y=-3x+2$ passant par deux points

$A$ et

$B$ dont les cordonnées respectives vérifient l'équation de la droite

$(\Delta).$ Donc,

si $x_{A}=0$ alors, en remplaçant dans l'équation de la droite de $(\Delta)$ on trouve $y_{A}=2$

et si $x_{B}=1$ alors, en remplaçant dans l'équation de la droite de $(\Delta)$ on trouve $y_{B}=-1.$ D'où,

$\begin{array}{|c|c|c|}\hline & A & B \\ \hline x & 0 & 1 \\ \hline y & 2 & -1 \\ \hline\end{array}$

III. Application affine par intervalle

Exemple :

Soit

$f$ une application définie par

$f(x)=|-3x+6|$

1) Montrons que

$f$ est une application affine par intervalle

On a

$-3x+6=0$ si, et seulement si,

$x=2$

$\begin{array}{|c|ccccr|}\hline x & -\infty & & 2 & & +\infty \\ \hline\text{signe de }-3x+6 & & + & 0 & - & \\ \hline f(x) & & -3x+6 &|& 3x-6 & \\ \hline\end{array}$

$x\in\;]-\infty\;;\ 2]\;,\ \ f(x)=-3x+6$

$x\in\;[2\;;\ +\infty[\;,\ \ f(x)=3x-6$

D'où,

$f$ est une application affine par intervalle.

2) Calculons

$f(0)\;,\ f(2)$ et

$f(3)$

On a

$f(x)=|-3x+6|$

Alors,

$f(0)=|-3(0)+6|=6$ ,

$f(2)=|-3(2)+6|=0$ et

$f(3)=|-3(3)+6|=3$

3) Sens de variation de

$f$

$x\in\;]-\infty\;;\ 2]\;,\ f$ est une application affine

$\searrow$

$x\in\;[2\;;\ +\infty[\;,\ f$ est une application affine

$\nearrow$

Tableau de variation

$\begin{array}{|c|ccccccccr|}\hline x & -\infty & & 0 & & 2 & & 3 & & +\infty \\ \hline & & & & &|& & & & \\ & & \searrow & & &|& & & \nearrow & \\ f & & & 6 & &|& & 3 & & \\ & & & &\searrow&|&\nearrow& & & \\ & & & & &0& & & & \\ \hline\end{array}$

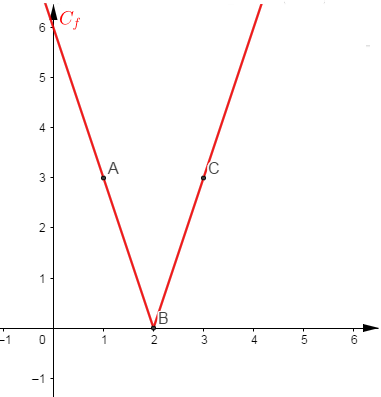
Représentons graphiquement

$f$

Représenter graphiquement

$f$ c'est représenter :

$(\Delta_{1})\;:\ y=-3x+6$ dans

$]-\infty\;;\ 2]$ et

$(\Delta_{2})\;:\ y=3x-6$ dans

$[2\;;\ +\infty[$

On a :

$\begin{array}{|c|c|c|}\hline & A & B \\ \hline x & 1 & 2 \\ \hline y & 3 & 0 \\ \hline\end{array}\qquad\qquad \begin{array}{|c|c|c|}\hline & B & C \\ \hline x & 0 & 3 \\ \hline y & 2 & 3 \\ \hline\end{array}$