Application et Polynôme - TL
Classe:
Terminale
1. Vocabulaire
Une fonction polynôme est une fonction $P$ définie sur $\mathbb{R}$ par : $P(x)=a_{n}x^{n}+a_{n}-1x^{n-1}+\ldots+a_{1}x a_{0}$ où $a_{n}\;,\ a_{n}-1\;,\ \ldots\;,\ a_{1}\;,\ a_{0}$ sont des nombres réels et $a_{n}$ est différent de $0.$
Les nombres $a_{n};,\ a_{n}-1\;,\ \ldots\;,\ a_{1}\;,\ a_{0}$ sont les coefficients du polynôme.
Une expression algébrique de la forme $a_{n}x^{n}$ est appelée monôme de degré $n.$
Un polynôme est une somme de monômes.
Toute solution de l'équation $P(x)=0$ est appelée racine du polynôme $P.$
Une fonction rationnelle est un quotient de deux polynômes.
Exemple :
Soit le polynôme $P(x)=4x^{3}-x^{2}+8x+1 .$
$P(x)$ est une somme algébrique de quatre monômes : $4x^{3}\;,\ -x^{2}\;,\ 8x$ et $1.$
Ces monômes sont rangés du plus haut au plus bas degré.
On dit que $P(x)$ est ordonné suivant les puissances décroissantes de $x$
Le monôme de plus haut degré de $P(x)$ est et il est de degré $3.$
On dit $P(x)$ est un polynôme de degré $3.$
On note deg$P=3.$
2. Développement, Réduction et ordination
Exemple :
Développer, réduire et ordonner les polynômes, puis indiquer leurs degrés :
$P(x)=\left(\dfrac{1}{2}x^{2}+3x-1\right)\left(-4x^{3}+6x-10\right)$
$Q(x)=3\left(x^{2}+2\right)^{2}-\left(x^{2}-3\right)(2-x).$
Réponses :
$(x)=-2x^{5}-12x^{4}+7x^{3}+13x^{2}-36x+10.\quad\text{deg}P=5$
$Q(x)=2x^{4}+3x^{3}+13x^{2}-9x+18.\quad\text{deg}Q=4.$
3. Égalité de deux polynômes
Propriété :
Deux polynômes sont égaux si et seulement si ils ont le même degré et si les coefficients des monômes de même degré sont égaux.
Exemple :
$P(x)=(x-2)^{2}+1$ et $Q(x)=(x-1)^{2}+6(x-1)+10$
Démontrer que $P(x)=Q(x).$
Réponse :
Après développement et réduction, on trouve que :
$P(x)=x^{2}+4x+5$ et $Q(x)=x^{2}+4x+5.$
Exercice d'application
Soient $a$, $b$ et $c$ des réels.
On donne les deux polynômes :
$P(x)=3x^{3}-x^{2}-9x-2$ et $Q(x)=ax^{3}+(b-2a)x^{2}+(c-2b)x-2c.$
Trouver $a$, $b$ et $c$ pour que les deux polynômes soient égaux.
Réponse :
Les deux polynômes ont même degré, donc d'après la propriété, on doit avoir :
$=a\ ; b-2a=-1\ ; c-2b=-9\ ; -2c=-2.$
4. Factorisation d'un polynôme par $(x-a)$
Théorème :
Si $a$ est racine du polynôme $P(x)$, alors il existe un polynôme $Q(x)$ tel que pour tout $x$ réel, $P(x)=(x-a)Q(x)$
On dit alors que P(x) est factorisable ou divisible par $(x-a).$
Remarque :
Dans ce cas, $\text{deg}Q=\text{deq}P-1.$ On dit que $Q$ est le quotient de la division de $P$ par $x-a.$
Méthodes pratiques pour factoriser par $(x-a)$
1. méthodes par identification ou méthode des coefficients indéterminés
Soit le polynôme $P(x)=2x^{4}+x^{3}-5x+2.$
On constate que le réel $1$ est racine.
En effet :
$P(1)=2(1)^{4}+(1)^{3}-5(1)+2=2+1-5+2=0.$
D'après le théorème précédent, il est possible de factoriser $P(x)$ par $(x-1)$ et d'après la remarque, le quotient $Q(x)$ est le degré $3$, donc de la forme $Q(x)=ax^{3}+bx^{2}+cx+d.$
Pour tout $x$ réel, on a :
$2x^{4}+x^{3}-5x+2=(x-1)\left(ax^{3}+bx^{2}+cx+d\right)=ax^{4}+(b-a)x^{3}+(c-b)x^{2}+(d-c)x-d.$
Ces deux polynômes sont égaux si et seulement si :
$$\left\lbrace\begin{array}{lcl} a&=&2\\ b-a&=&1\\ c-b&=&0\\ d-c&=&-5\\ d&=&-2\\ \end{array}\right.$$
Soit $a=2$, $b=-2$, $c=3$ et $b=3$
Ainsi $Q(x)=2x^{3}+3x^{2}+3x-3$ et $P(x)=(x-1)\left(2x^{3}+3x^{2}+3x-3\right)$
2. Méthode par division
Reprenons le polynôme défini par : $P(x)=2x^{4}+x^{3}-5x+2$
Pour obtenir le polynôme $Q(x)$, on utilise la disposition pratique suivante (division euclidienne) :
$$\begin{array}{r} 2x^{4}+x^{3}-5x+2\\\\\\ \end{array}\begin{array}{|l}x-1\\ \hline \\\\ \end{array}$$
$$\begin{array}{r} 2x^{4}+x^{3}-5x+2\\\\\\ \end{array}\begin{array}{|l}x-1\\ \hline \\\\ \end{array}$$
$$\begin{array}{r}-2x^{4}+2x^{3}\\ \hline \\0+3x^{3}-5x+2\\-3x^{3}+3x^{2}\\ \hline\\0+3x^{2}-5+2\\-3x^{2}+3\\ \hline\\-2x+2\\2x-2\\\hline\\0\end{array}\begin{array} {|l}2x^{3}+3x^{2}+3x-3\\ \hline \\\\ \\\\ \\\\ \\\\\\ \\\\ \end{array}$$
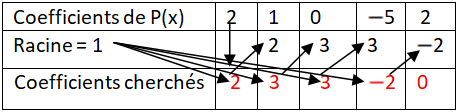
3. Méthode de HÖrner
Reprenons toujours le polynôme $P(x)=2x_{4}+3x_{3}-5x+2.$
Pour montrer que $(1)=0$ et calculer les coefficients du quotient, on peut disposer les calculs comme dans le tableau qui suit, appelé tableau de Hörner :
4. Systèmes
Notions sur les systèmes d'équations
On appelle système de deux équations à deux inconnues $x$ et $y$ tout système de la forme :
$$\left\lbrace\begin{array}{lcl} ax+by+c&=&0\\a'x+b'y+c'&=&0 \end{array}\right.$$
Résoudre un tel système dans $\mathbb{R}^{2}$, c'est trouver l'ensemble des couples $(x\;,\ y)$ de $\mathbb{R}^{2}$ qui vérifient simultanément les deux équations.
Cela se ramène à chercher l'intersection des deux droites du plan d'équations : $ax+by+c=0$ et $a'x+b'y+c'=0.$
Celles-ci peuvent être soit sécantes (dans ce cas, le système admet un couple solution unique), soit strictement parallèles (dans ce cas, le système n'admet pas de solution), soit confondues (dans ce cas, le système admet une infinité de solutions).
On appelle système de trois équations à trois inconnues $x$, $y$ et $z$ tout système de la forme :
$$\left\lbrace\begin{array}{lcl} ax+by+c&=&0\\a'x+b'y+c'&=&0\\a''x+b''y+c''&=&0 \end{array}\right.$$
Méthodes de résolution
$\bullet\ $Pour les systèmes à deux inconnues :
1) Méthode de substitution
Cette méthode consiste à exprimer une inconnue en fonction de l'autre à partir d'une équation et à substituer dans l'autre équation.
Exemple :
Soit le système : $\left\lbrace\begin{array}{lcl} x+2y+3&=&0\quad(1)\\2x-y-4&=&0\quad(2) \end{array}\right.$
On isole $x$ dans $(1)$ : $x=-2y-3.$
On remplace $x$ par $-2y-3$ dans $(2)$ pour obtenir :
$2(-2y-3)-y-4=0$, soit $-5y-10=0$ et donc $y=2.$
Comme $x=-22y-3$, on a $x=1.$
Ainsi le couple solution du système est $(1\;,\ -2).$
2) Méthode d'addition ou de combinaisons linéaires
Exemple :
Reprenons le système : $\left\lbrace\begin{array}{lcl} x+2y+3&=&0\quad(1)\\2x-y-4&=&0\quad(2) \end{array}\right.$
$\ast\ $On multiplie l'équation $(1)$ par $2$ et l'équation $(2)$ par $(-1).$
On obtient : : $\left\lbrace\begin{array}{lcl} 2x+4y+6&=&0\\-2x+y+4&=&0 \end{array}\right.$
On additionne, les $x$ s'éliminent : $5y+10=0$, soit $y=-2.$
$\ast\ $On multiplie l'équation $(2)$ par $2.$
On obtient : $\left\lbrace\begin{array}{lcl} x+2y+3&=&0\\4x-2y-8&=&0 \end{array}\right.$
On additionne, les $y$ s'éliminent : $5x-5=0$, soit $x=1.$
Après vérification (indispensable dans cette méthode !) on conclut que le couple solution du système est $(1\;,\ 2).$
2) Méthode graphique
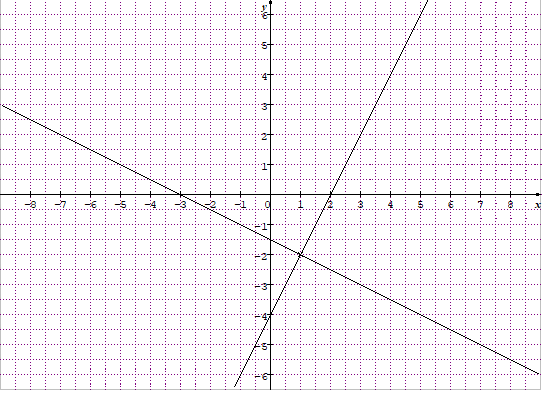
Pour résoudre le système, on trace les droites $\mathfrak{D}_{1}$ et $\mathfrak{D}_{2}$ d'équations respectives : $x+2y+3=0$ et $2x-y-4=0.$
Rappelons que pour tracer une droite, il suffit de déterminer les coordonnées $(x\;,\ y)$ de deux points de cette droite en donnant à $x$ ou à $y$ des valeurs arbitraires.
Pour $\mathfrak{D}_{1}$, on peut prendre les couples $\left(0\;,\ -\dfrac{3}{2}\right)$ et $(3\;,\ -3).$
Pour $\mathfrak{D}_{2}$, on peut prendre $(2\;,\ 0)$ et $(3\;,\ 2).$
On lit sur la figure les coordonnées du point d'intersection qui constituent le couple solution du système
$\ast\ $Pour les systèmes à trois inconnues :
Comme pour les systèmes à deux inconnues, on peut utiliser la méthode de substitution ou la méthode de combinaison, mais on utilise plus fréquemment la méthode du pivot de Gauss.
Celle-ci permet de transformer tout système de trois équations à trois inconnues en un système plus facile à résoudre et qui a les mêmes solutions.
On dit que les deux systèmes sont équivalents.
On admet que si l'on fait l'une des opérations suivantes dans un système, on obtient un système équivalent :
I. permuter deux lignes,
II. multiplier ou diviser une ligne par un réel non nul,
III. ajouter ou soustraire à une ligne un multiple d'une autre ligne.
Soit à résoudre dans $\mathbb{R}^{3}$ le système : $\left\lbrace\begin{array}{lcl} -3x+y-2z&=&-1\quad L_{1}\\2xx-3y+8z&=&16\quad L_{2}\\x-2y+5z&=&10\quad L_{3} \end{array}\right.$
$$\begin{array}{|l|l|l|} \hline \text{Opération effectuée}&\text{Notation}&\text{Système équivalent obtenu}\\ \hline \text{On permute les lignes}&L_{1}\;\leftrightarrow\;L_{3}&\left\lbrace\begin{array}{lcl} x-2y+5z&=&10\quad L_{1}\\2x-3y+8z&=&16\quad L_{2}\\-3x+y-2z&=&-1\quad L_{3} \end{array}\right.\\ L_{1}\quad\text{et}\quad L_{3}&&\\\hline \text{On soustrait deux fois}&L_{2}\leftarrow\;L_{2}-2\times\;L_{1}&\left\lbrace\begin{array}{lcl} x-2y+5z&=&10\quad L_{1}\\y-2z&=&-4\quad L_{2}\\-3x+y-2z&=&-1\quad L_{3} \end{array}\right.\\ \text{la ligne }L_{1}\text{ à la ligne }L_{2}&&\\ \hline \text{On ajoute trois fois}&L_{3}\leftarrow\;L_{3}+3\times\;L_{1}&\left\lbrace\begin{array}{lcl} x-2y+5z&=&10\quad L_{1}\\y-2z&=&-4\quad L_{2}\\-5y+13z&=&29\quad L_{3} \end{array}\right.\\ \text{la ligne }L_{1}\text{ à la ligne }L_{3}&&\\ \hline \text{On ajoute cinq fois}&L_{3}\leftarrow\;L_{3}+5\times\;L_{2}&\left\lbrace\begin{array}{lcl} x-2y+5z&=&10\quad L_{1}\\y-2z&=&-4\quad L_{2}\\ 3z&=&9\quad L_{3} \end{array}\right.\\ \text{la ligne }L_{2}\text{ à la ligne }L_{3}&&\\ \hline \end{array}$$
On obtient alors un système dit triangulaire que l'on résout facilement.
De la dernière équation, on tire $z=3$, et, en remontant on en déduit que $y=2$, puis $x=1.$
Conclusion : $S=\left\lbrace(-1\;,\ 2\;,\ 3)\right\rbrace$

Commentaires
You (non vérifié)
jeu, 07/25/2024 - 01:22
Permalien
Merci le site est tellement
Ajouter un commentaire