I. Notion de vecteur
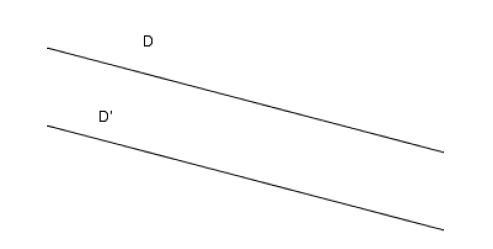
On dit que deux droites $(\mathcal{D})$ et $(\mathcal{D'})$ ont même direction si elles sont parallèles (ou confondues).
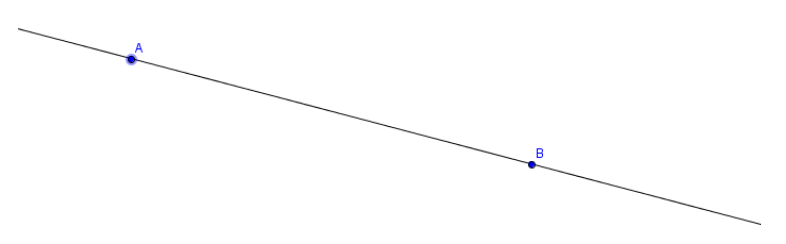
Sur une droite $(AB)$ ; on admet par convention qu'il y a deux sens de parcours possibles (de $A$ vers $B$ ou de $B$ vers $A).$
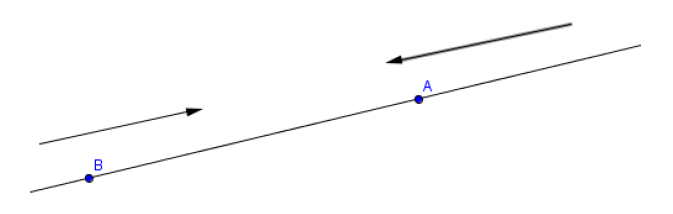
Un axe est une droite sur laquelle on a choisi (une fois pour toutes) un sens de parcours.
Un bipoint $(A\;,\ B)$ est un couple de points du plan donnés dans cet ordre.
Le bipoint $(A\;,\ B)$ est donc différent du bipoint $(B\;,\ A).$
Soient $A$ et $B$ deux points d'un axe $(\mathcal{D}).$
On appelle mesure algébrique du bipoint $(A\;,\ B)$ et on note $\overline{AB}$ le réel égal à :
$\bullet\ $ $+AB$ si le sens de l'axe est celui de $A$ vers $B.$
$\bullet\ $ $-AB$ si le sens de l'axe est celui de $B$ vers $A.$
On a la relation de Chasles pour les mesures algébriques :
$$\overline{AB}+\overline{BC}=\overline{AC}$$
pour trois points quelconques $A$, $B$ et $C$ d'un même axe.
Sur une demi-droite $[Ax)$, on admet, par convention qu'il n y a qu'un seul sens de parcours.
Définition :
Soit $(A\;,\ B)$ un bipoint donné du plan.
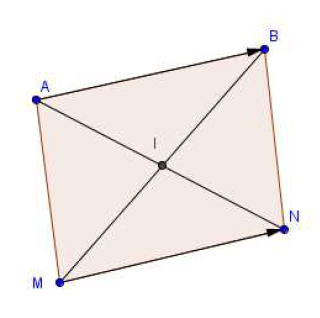
L'ensemble de tous les bipoints $(M\;,\ N)$ tels que les segments $[AN]$ et $[BM]$ aient le même milieu est un objet mathématique appelé vecteur $\overrightarrow{AB}.$
Dire que $\overrightarrow{AB}=\overrightarrow{MN}$ signifie que :
$$\left\lbrace\begin{array}{l} -\ \text{Les droites }(AB)\text{ et }(MN)\text{ ont même direction}\\ -\ \text{Les demi-droites }[AB)\text{ et }[MN)\text{ ont même sens} \end{array}\right.$$
N.B.
Ces conditions équivalentes au fait que $ABNM$ est un parallélogramme, éventuellement aplati.
Elles sont aussi équivalentes à l'une quelconque des conditions suivantes :
$\bullet$ $\overrightarrow{AM}=\overrightarrow{BN}$
$\bullet$ $\overrightarrow{AN}=\overrightarrow{AB}+\overrightarrow{AM}$
$\bullet$ $\overrightarrow{BM}=\overrightarrow{BA}+\overrightarrow{BN}$
La distance $AB$ est appelée norme du vecteur $\overrightarrow{AB}$ et notée $\|\overrightarrow{AB}\|$
Un vecteur est caractérisé par sa direction, son sens et sa norme.
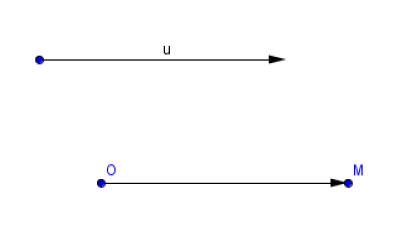
Propriété (Axiome d'EUCLIDE)
Étant donnés un point $O$ et un vecteur $\vec{u}$, il existe un unique point $M$ du plan tel que :
$\overrightarrow{OM}=\vec{u}.$
Rappelons qu'en Mathématiques, un axiome est une proposition « évidente » dont la vérité est admise sans démonstration.
II. Opérations sur les vecteurs
1) Addition des vecteurs
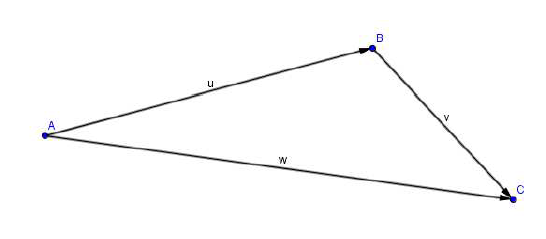
Soient $\vec{u}$ et $\vec{v}$ deux vecteurs donnés et $A$ un point fixe.
Il existe, d'après l'Axiome d'Euclide précédent, un point $B$ unique tel que $\overrightarrow{AB}=\vec{u}$ et, toujours selon cet axiome, un point $C$ unique tel que $\overrightarrow{BC}=\vec{v}.$
Par définition, le vecteur $\overrightarrow{AC}$ est la somme des vecteurs $\vec{u}$ et $\vec{v}.$
On a donc :
$\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$ (relation de Chasles).
Propriétés :
a) La commutativité :
Pour tous vecteurs $\vec{u}$ et $\vec{v}$, on a :
$$\boxed{\vec{u}+\vec{v}=\vec{v}+\vec{u}}$$
b) L'associativité :
Pour tous vecteurs $\vec{u}$, $\vec{v}$ et $\vec{w}$, on a :
$$\boxed{\vec{u}+(\vec{v}+\vec{w})=(\vec{u}+\vec{v})+\vec{w}}$$
c) L'existence d'un élément neutre :
Le vecteur associé aux bipoints de la forme $(A\;,\ A)$ est appelé vecteur nul et noté $\vec{0}.$
Quel que soit le vecteur $\vec{u}$, on a :
$$\boxed{\vec{u}+\vec{0}=\vec{0}+\vec{u}=\vec{u}}.$$
d) Symétrique d'un élément
Quel que soit le vecteur $\vec{u}$, il existe un vecteur noté $(-\vec{u})$ tel que :
$$\boxed{\vec{u}+(-\vec{u})=(-\vec{u})+\vec{u}=\vec{0}}$$
$(-\vec{u})$ est l'opposé du vecteur $\vec{u}.$
Il a même direction et même sens que $\vec{u}$, mais son sens est opposé à celui de $\vec{u}.$
On a :
$\overrightarrow{AB}=-\overrightarrow{BA}.$
La différence de deux vecteurs $\vec{u}$ et $\vec{v}$ dans cet ordre est, par définition, la somme du premier et de l'opposé du second.
Elle est notée :
$$\boxed{\vec{u}-\vec{v}=\vec{u}+(-\vec{v})}$$
2) Multiplication d'un vecteur par un réel
Définition :
Soit $t$ un réel et $\vec{u}$ un vecteur.
On appelle produit du réel $t$ par le vecteur $\vec{u}$ et on note $t\cdot\vec{u}$ le vecteur défini de la manière suivante :
$\ast$ Si $t=0$, alors, on pose : $t\cdot\vec{u}=\vec{0}.$
$\ast$ Si $t\neq 0$, $t\cdot\vec{u}$ est le vecteur qui a :
$-\ $ pour direction celle de $\vec{u}$
$-\ $ pour sens $$\left\lbrace\begin{array}{lcl} -\ \text{celui de }\vec{u}&\text{si}&t>0\\ -\ \text{le sens contraire de }\vec{u}&\text{si}&t<0 \end{array}\right.$$
Propriétés :
Pour tous réels $t$ et $t'$ et tous vecteurs $\vec{u}$ et $\vec{v}$, on a :
a) $(t+t')\cdot\vec{u}=t\cdot\vec{u}+t'\cdot\vec{u}$
b) $t(\vec{u}+\vec{v})=t\cdot\vec{u}+t\cdot\vec{v}$
c) $t(t'\cdot\vec{u})=(tt')\vec{u}$
d) $1\cdot\vec{u}=\vec{u}$
Ces propriétés permettent de faire tous les calculs algébriques sur les vecteurs.
Vecteurs colinéaires
Deux vecteurs $\vec{u}$ et $\vec{v}$ sont dites colinéaires si et seulement si :
$$\left\lbrace\begin{array}{l} -\ \text{l'un deux est nul}\\ \qquad\text{ou bien}\\ -\ \text{Il existe un réel }k\text{ tel que }\vec{u}=k\vec{v} \end{array}\right.$$
On a les résultats suivants (cf. cours de Seconde) :
$\bullet$ Les droites $(AB)$ et $(CD)$ sont parallèles si et seulement si les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{CD}$ sont colinéaires.
En particulier, trois points $A$, $B$ et $C$ sont alignés si et seulement si les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ sont colinéaires.
$\bullet$ La droite $(AB)$ est l'ensemble des points $M$ tels que $\overrightarrow{AM}$ et $\overrightarrow{AB}$ soient colinéaires.
III. Projection et énoncés de THALES
1) Notion de projection
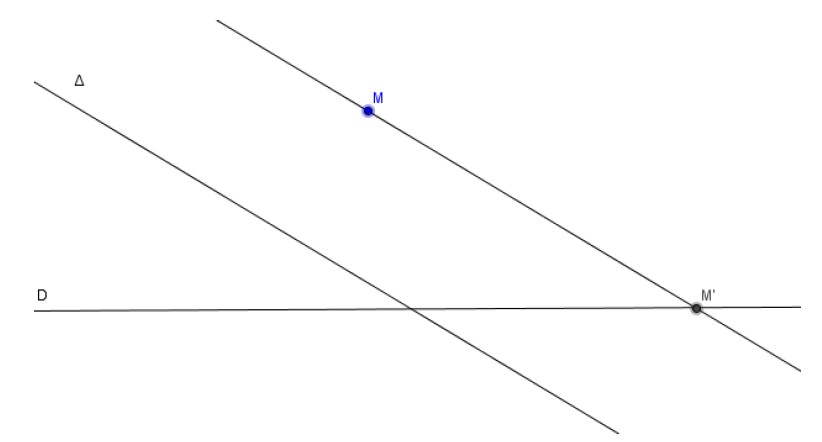
Soient $(\mathcal{D})$ et $(\Delta)$ deux droites et $M$ un point du plan.
On appelle projeté de $M$ sur $(\mathcal{D})$ parallèlement à $(\Delta)$ le point $M'$, intersection de $(\mathcal{D})$ avec la parallèle à $(\Delta)$ passant par $M.$
On note alors $M'=p(M).$
N.B.
a) L'existence de $M'$ est justifiée par le résultat suivant :
« Quand deux droites sont sécantes, toute parallèle à l’une est sécante à l'autre ».
b) Si $M\in\Delta$, on a $M'=M.$
2) Théorème de Thalès
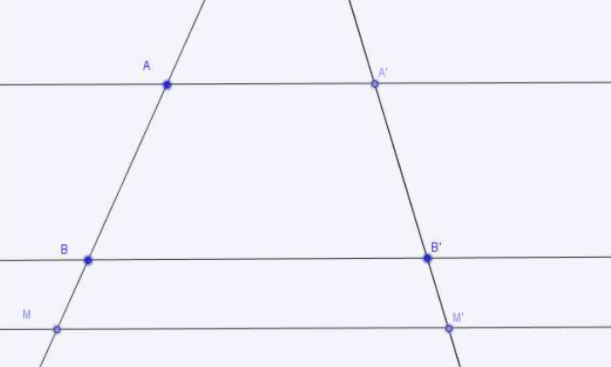
Soient $(\mathcal{D})$ et $(\Delta)$ deux axes ; $A$, $B$ et $M$ trois points de $(\mathcal{D})$ de projetés respectifs $A'$, $B'$ et $M'$ sur $(\Delta)$ parallèlement à une troisième droite $(\delta).$
Alors on a l'égalité :
$$\dfrac{\overline{AM}}{\overline{AB}}=\dfrac{\overline{A'M'}}{\overline{A'B'}}$$
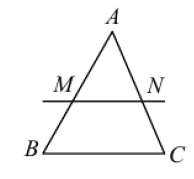
Cas particulier :
Dans la configuration ci-dessous :
On a $\dfrac{\overline{AM}}{\overline{AB}}=\dfrac{\overline{AN}}{\overline{AC}}$ et de plus, en utilisant une propriété des quotients de réels vue en Seconde, ce rapport est aussi égal à $\dfrac{\overline{AN}-\overline{AM}}{\overline{AC}-\overline{ABA}}$ c'est-à-dire à $\dfrac{\overline{MN}}{\overline{BC}}.$
3) Réciproque du théorème de Thalès
Soient $(\mathcal{D})$ et $(\Delta)$ deux axes ; $A$ et $B$ deux points de $(\mathcal{D})$ de projetés respectifs $A'$ et $B'$ sur $(\Delta)$ parallèlement à une troisième droite $(\delta).$
$M$ et $M'$ sont deux points de $(\mathcal{D})$ et $(\Delta)$ respectivement tels que :
$$\dfrac{\overline{AM}}{\overline{AB}}=\dfrac{\overline{A'M'}}{\overline{A'B'}}$$
Alors on a : $p(M)=M'.$
En d'autres termes les droites $(MM')$, $(AA')$ et $(BB')$ sont parallèles.
IV. Barycentre de plusieurs points
La notion de barycentre de $2$ ou $3$ points pondérés, étudiée en Seconde, peut être étendue à $4$, $5$, $\ldots$, $n$ points.
Dans l'exposé qui suit, nous présentons les résultats avec $4$ points, mais ils restent valables avec un nombre quelconque de points.
1) Théorème et définition
Soient $\alpha$, $\beta$, $\gamma$ et $\delta$ des réels dont la somme n'est pas nulle (i.e. $\alpha+\beta+\gamma+\delta)\neq 0$ et $A$, $B$, $C$, $D$ des points du plan.
Il existe un point unique $G$ tel que :
$$\alpha\overrightarrow{GA}+\beta\overrightarrow{GB}+\gamma\overrightarrow{GC}+\delta\overrightarrow{GD}=\overrightarrow{0}\quad(1)$$
Le point $G$ défini par la relation $(1)$ est appelé barycentre du système de points pondérés ${(A\;,\ \alpha)\ ;\ (B\;,\ \beta)\ ;\ (C\;,\ \gamma)\ ;\ (D\;,\ \delta)}.$
Démonstration :
$\begin{array}{rcl} \alpha\overrightarrow{GA}+\beta\overrightarrow{GB}+\gamma\overrightarrow{GC}+\delta\overrightarrow{GD}=\vec{0} &\Leftrightarrow & \alpha\overrightarrow{GA}+\beta\left(\overrightarrow{GA}+\overrightarrow{AB}\right)+\gamma\left(\overrightarrow{GA}+\overrightarrow{AC}\right)+\delta\left(\overrightarrow{GA}+\overrightarrow{AD}\right)=\vec{0}\\\\ &\Leftrightarrow &(\alpha+\beta+\gamma+\delta)\overrightarrow{GA}+\beta\overrightarrow{AB}+\gamma\overrightarrow{AC}+\delta\overrightarrow{AD}=\overrightarrow{0}\\\\ &\Leftrightarrow &(\alpha+\beta+\gamma+\delta)\overrightarrow{AG}=\beta\overrightarrow{AB}+\gamma\overrightarrow{AC}+\delta\overrightarrow{AD}\\\\ &\Leftrightarrow & \overrightarrow{AG}=\dfrac{\beta}{\alpha+\beta+\gamma+\delta}\overrightarrow{AB}+\dfrac{\gamma}{\alpha+\beta+\gamma+\delta}\overrightarrow{AC}+\dfrac{\delta} {\alpha+\beta+\gamma+\delta}\overrightarrow{AD}\quad(2)\end{array}$
Car, par hypothèse la somme $(\alpha+\beta+\gamma+\delta)$ n'est pas nulle.
Soit $\overrightarrow{V}$ le vecteur au second membre de $(2).$
$\overrightarrow{V}$ est un vecteur fixe puisque $A$, $B$, $C$, $D$ et $\alpha$, $\beta$, $\gamma$ et $\delta$ sont donnés.
D'après l'Axiome d'EUCLIDE, cf. paragraphe 1, il existe un unique point $G$ tel que :
$$\overrightarrow{AG}=\overrightarrow{V}$$
N.B.
La relation $(2)$ de la démonstration précédente permet de construire vectoriellement le barycentre de plusieurs points.
On a aussi les relations analogues :
$\overrightarrow{BG}=\dfrac{\alpha}{\alpha+\beta+\gamma+\delta}\overrightarrow{BA}+\dfrac{\gamma}{\alpha+\beta+\gamma+\delta}\overrightarrow{BC}+\dfrac{\delta}{\alpha+\beta+\gamma+\delta}\overrightarrow{BD}$
$\overrightarrow{CG}=\dfrac{\alpha}{\alpha+\beta+\gamma+\delta}\overrightarrow{CA}+\dfrac{\beta}{\alpha+\beta+\gamma+\delta}\overrightarrow{CB}+\dfrac{\delta}{\alpha+\beta+\gamma+\delta}\overrightarrow{CD}$
2) Homogénéité du barycentre
Le barycentre de plusieurs points reste inchangé lorsqu'on multiplie tous les coefficients par un même nombre non nul.
En effet soit $G$ le barycentre du système ${(A\;,\ \alpha)\ ;\ (B\;,\ \beta)\ ;\ (C\;,\ \gamma)\ ;\ (D\;,\ \delta)}$ et $k$ un réel non nul.
On a :
$\begin{array}{rcl} \alpha\overrightarrow{GA}+\beta\overrightarrow{GB}+\gamma\overrightarrow{GC}+\delta\overrightarrow{GD}=\vec{0}&\Rightarrow & k\left(\alpha\overrightarrow{GA}+\beta\overrightarrow{GB}+\gamma\overrightarrow{GC}\delta\overrightarrow{GD}\right)=\vec{0}\\\\&\Rightarrow & (k\alpha)\overrightarrow{GA}+(k\beta)\overrightarrow{GB}+(k\gamma)\overrightarrow{GC}+(k\delta)\overrightarrow{GD}=\vec{0}\end{array}$
Et la somme $(k\alpha+k\beta+k\gamma+k\delta)=k(\alpha+\beta+\gamma+\delta)$ est non nulle par hypothèse.
Donc $G$ est aussi le barycentre du système ${(A\;,\ k\alpha)\ ;\ (B\;,\ k\beta)\ ;\ (C\;,\ k\gamma)\ ;\ (D\;,\ k\delta)}.$
Cas particulier :
Si tous les coefficients sont égaux et non nuls (i.e. $\alpha=\beta=\gamma=\delta$ et $\alpha\neq 0)$, le barycentre du système ${(A\;,\ \alpha)\ ;\ (B\;,\ \alpha)\ ;\ (C\;,\ \alpha)\ ;\ (D\;,\ \alpha)}$ est aussi celui de ${(A\;,\ 1)\ ;\ (B\;,\ 1)\ ;\ (C\;,\ 1)\ ;\ (D\;,\ 1)}.$
N.B.
Il est confondu avec le milieu du segment $[AB]$ dans le cas d'un système de deux points distincts, avec le centre de gravité du triangle $ABC$ dans le cas d'un système de trois points non alignés, avec le point de concours des diagonales dans le cas d'un système de $4$ points formant un parallélogramme.
3) Réduction du vecteur
$\overrightarrow{V_{M}}=\alpha\overrightarrow{MA}+\beta\overrightarrow{MB}+\gamma\overrightarrow{MC}+\delta\overrightarrow{MD}$, $M$ point quelconque du plan
$1^{er}$ cas : Si $(\alpha+\beta+\gamma+\delta)\neq 0$ :
Soit alors $G$ le barycentre du système ${(A\;,\ \alpha)\ ;\ (B\;,\ \beta)\ ;\ (C\;,\ \gamma)\ ;\ (D\;,\ \delta)}.$
$G$ existe d'après le théorème du 1)
On peut écrire d'après la relation de CHASLES :
$\begin{array}{rcl}\overrightarrow{V_{M}}&=&\alpha\left(\overrightarrow{MG}+\overrightarrow{GA}\right)+\beta\left(\overrightarrow{MG}+\overrightarrow{GB}\right)+\gamma\left(\overrightarrow{MG}+\overrightarrow{GC}\right)+\delta\left(\overrightarrow{MG}+\overrightarrow{GD}\right)\\ \\&=&(\alpha+\beta+\gamma+\delta)\overrightarrow{MG}+\underbrace{\alpha\overrightarrow{GA}+\beta\overrightarrow{GB}+\gamma\overrightarrow{GC}+\delta\overrightarrow{GD}}_{=\overrightarrow{0}\text{ par définition de }G}\end{array}$
Ainsi, dans ce cas, le vecteur $\overrightarrow{V_{M}}$ se réduit à :
$$\overrightarrow{V_{M}}=(\alpha+\beta+\gamma+\delta)\overrightarrow{MG}.$$
On retiendra que : si le système ${(A\;,\ \alpha)\ ;\ (B\;,\ \beta)\ ;\ (C\;,\ \gamma)\ ;\ (D\;,\ \delta)}$ a un barycentre, alors pour tout point $M$ du plan, on a :
$$\alpha\overrightarrow{MA}+\beta\overrightarrow{MB}+\gamma\overrightarrow{MC}+\delta\overrightarrow{MD}=(\alpha+\beta+\gamma+\delta)\overrightarrow{MG}$$
$2^{ième}$ cas : Si $(\alpha+\beta+\gamma+\delta)=0$ :
Soit $N$ un autre point du plan.
On peut écrire :
$\begin{array}{rcl}\overrightarrow{V_{M}}&=&\alpha\left(\overrightarrow{MN}+\overrightarrow{NA}\right)+\beta\left(\overrightarrow{MN}+\overrightarrow{NB}\right)+\gamma\left(\overrightarrow{MN}+\overrightarrow{NC}\right)+\delta\left(\overrightarrow{MN}+\overrightarrow{ND}\right)\\ \\&=&\underbrace{(\alpha+\beta+\gamma+\delta)\overrightarrow{MN}}_{=\overrightarrow{0}\text{ car par hypothèse }(\alpha+\beta+\gamma+\delta)=0}+\underbrace{\alpha\overrightarrow{NA}+\beta\overrightarrow{NB}+\gamma\overrightarrow{NC}+\delta\overrightarrow{ND}}_{=\overrightarrow{V_{N}}}\end{array}$
Ainsi, dans ce cas, si $M$ et $N$ sont deux points quelconques du plan, on a : $\overrightarrow{V_{M}}=\overrightarrow{V_{N}}.$
Donc $\overrightarrow{V_{M}}$ est un vecteur constant.
Il est égal, par exemple, à $\beta\overrightarrow{AB}+\gamma\overrightarrow{AC}+\delta\overrightarrow{AD}$ ($M$ remplacé par $A).$
4) Associativité du barycentre
Exemple :
Soient $A$, $B$, $C$, $D$ quatre points du plan et $G$ le barycentre du système
$$S={(A\;,\ -1)\ ;\ (B\;,\ 2)\ ;\ (C\;,\ -1)\ ;\ (D\;,\ 3)}.$$
$G$ existe car : $-1+2+(-1)+3=3\neq 0.$
Les systèmes de $2$ points pondérés $S_{1}={(A\;,\ -1)\ ;\ (B\;,\ 2)}$ et $S_{2}={(C\;,\ -1)\ ;\ (D\;,\ 3)}$ ont aussi des barycentres que nous désignerons respectivement par $I$ et $J.$
D'après le paragraphe précédent 3), on a pour tout point $M$ du plan :
$-\overrightarrow{MA}+2\overrightarrow{MB}=\overrightarrow{MI}\quad(1)\text{ et }-\overrightarrow{MC}+3\overrightarrow{MD}=2\overrightarrow{MJ}\quad(2).$
Remplaçons $M$ par $G$ dans ces deux relations et faisons la somme membre à membre.
On obtient ainsi :
$\underbrace{-\overrightarrow{GA}+2\overrightarrow{GB}-\overrightarrow{GC}+3\overrightarrow{GD}}_{=\vec{0}\text{ par défition de }G}=\overrightarrow{GI}+2\overrightarrow{GJ}.$
On en déduit que :
$\overrightarrow{GI}+2\overrightarrow{GJ}=\vec{0}$ et par conséquent $G$ est le barycentre du système $S'={(I\;,\ 1)\ ;\ (J\;,\ 2)}.$
On notera que les coefficients $1$ et $2$ sont respectivement la somme des coefficients des systèmes $S_{1}$ et $S_{2}.$
D'autre part, soit $K$ le barycentre du système $S_{3}={(B\;,\ 2)\ ;\ (C\;,\ -1)\ ;\ (D\;,\ 3)}.$
Pour tout point $M$ du plan, on a, toujours d'après le paragraphe 3), $2\overrightarrow{MB}-\overrightarrow{MC}+3\overrightarrow{MD}=4\overrightarrow{MK}.$
Remplaçant $M$ par $G$, on obtient : $2\overrightarrow{GB}-\overrightarrow{GC}+3\overrightarrow{GD}=\overrightarrow{GK}$ et si on ajoute le vecteur $-\overrightarrow{GA}$ aux deux membres de cette dernière égalité, on a :
$\underbrace{-\overrightarrow{GA}+2\overrightarrow{GB}-\overrightarrow{GC}+2\overrightarrow{GD}}_{=\overrightarrow{0}\text{ par définition de }G}=-\overrightarrow{GA}+4\overrightarrow{GK}.$
On en déduit que $G$ est aussi le barycentre du système $S''={(A\;,\ -1)\ ;\ (K\;,\ 4)}.$
En généralisant ces calculs, on retiendra que dans la recherche du barycentre de plusieurs points, on peut regrouper certains d'entre eux et les remplacer par leur barycentre partiel affecté de la somme de leurs coefficients (pourvu que celle(ci ne soit pas nulle).
4) Centre d'inertie d'une plaque homogène
La notion de centre d'inertie d'un solide provient de la Physique.
Galilée $(1564-1642)$ établit que le mouvement d'un solide, aussi compliqué soit-il, peut être étudié de façon plus simple en considérant la trajectoire de son centre d'inertie.
Une plaque homogène est un solide dont la masse de toute portion est proportionnelle à l'aire de celle-ci.
Pour en déterminer le centre d'inertie, on utilise les principes suivants, que nous admettrons :
(1) si la plaque admet un centre de symétrie, c'est aussi le centre d'inertie (exemple : point d'intersection des diagonales dans un parallélogramme).
(2) si la plaque admet un axe de symétrie, le centre d'inertie appartient à cet axe (exemple : trapèze isocèle) ;
(3) une plaque triangulaire admet pour centre d'inertie son centre de gravité.
(4) si une plaque est formée par la réunion de deux plaques $P_{1}$ et $P_{2}$ de centres d'inertie respectifs $G_{1}$ et $G_{2}$ et de masses respectives $m_{1}$ et $m_{2}$, alors son centre d'inertie est le barycentre des points pondérés $\left(G_{1}\ ;\ m_{1}\right)$ et $\left(G_{2}\ ;\ m_{2}\right)$
(5) si une plaque est formée par une plaque $\mathcal{P}_{1}$ de centre d'inertie $G_{1}$ et d'aire $\mathcal{A}_{1}$ dont on enlève une plaque $\mathcal{P}_{2}$ de centre d'inertie $G_{2}$ et d'aire $\mathcal{A}_{2}$, on obtient une plaque évidée $\mathcal{P}$ dont le centre d'inertie est le barycentre de $\left(G_{1}\ ;\ \mathcal{A}_{1}\right)$ et de $\left(G_{2}\ ;\ -\mathcal{A}_{2}\right).$
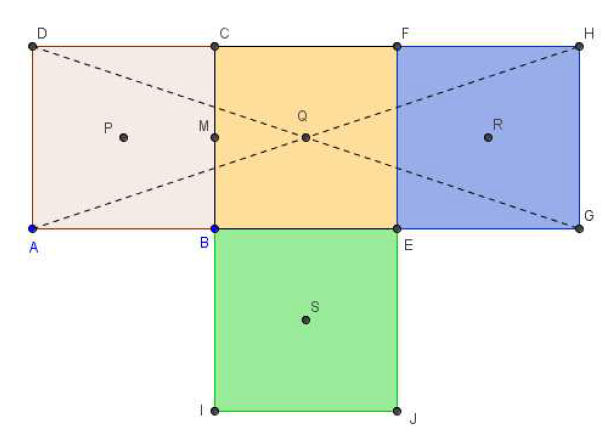
Exemple 1
La plaque homogène ci-dessous est composée de quatre parties carrées superposables.
1) Sans faire aucun calcul, construire son centre d'inertie $U.$
2) Démontrer que le centre d'inertie $U$ est le milieu de $[ME].$
1) On peut considérer la plaque comme la superposition de la plaque rectangulaire $DHGA$ (elle-même superposition des trois carrés $DCBA$, $CFEB$ et $FHGE)$ et de la plaque carrée $BEJI.$
Pour des raisons de symétrie, il est clair que $DHGA$ a pour centre de symétrie $Q$ et que la plaque $BEJI$ a pour centre de symétrie $S$ (principe (1)).
Le centre de symétrie ou d'inertie de la plaque est donc (principe 4) le barycentre de ${(Q\;,\ 3)\ ;\ (S\;,\ 1)}.$
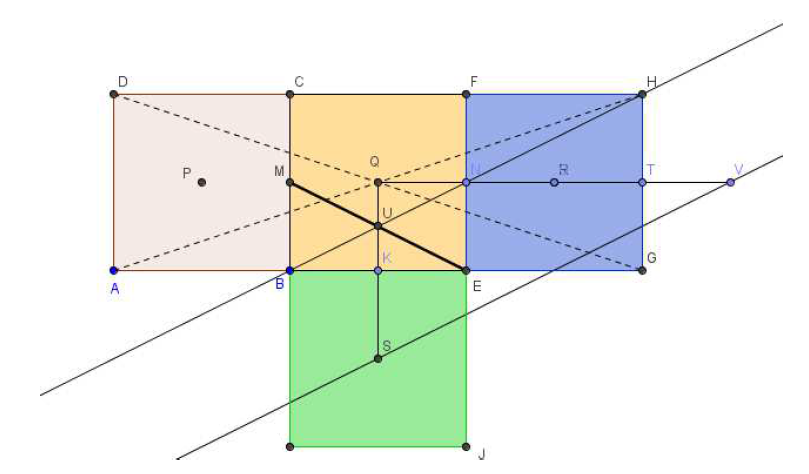
La figure ci-dessous illustre la construction du centre d'inertie $U$ (les droites $(BH)$ et $(SV)$ sont parallèles).
2) On a $\overrightarrow{QU}=\dfrac{1}{4}\overrightarrow{QS}=\dfrac{1}{4}\overrightarrow{DA}$ et
$\overrightarrow{QM}+\overrightarrow{QE}=-\dfrac{1}{2}\overrightarrow{AB}+\overrightarrow{QK}+\overrightarrow{KE}=-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{DA}+\dfrac{1}{2}\overrightarrow{AB}=\dfrac{1}{2}\overrightarrow{DA}.$
Ainsi $\overrightarrow{QU}=\dfrac{1}{2}\left(\overrightarrow{QM}+\overrightarrow{QE}\right).$
$U$ est bien le milieu de $[ME].$
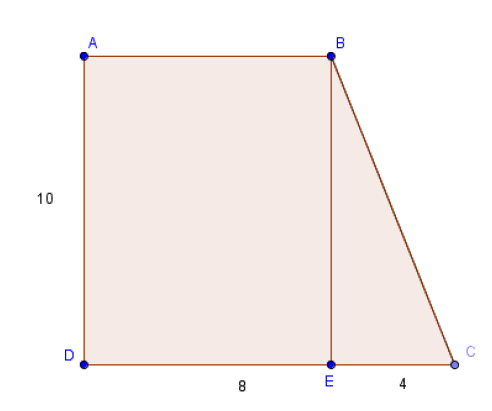
Exemple 2
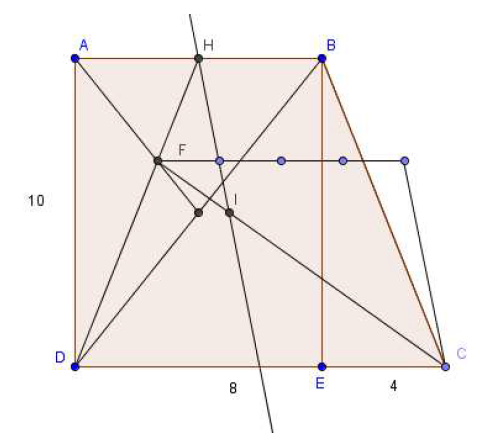
On considère la plaque trapézoïdale homogène $ABCD$ ci-dessous.
1) Construire le centre d'inertie $G$ de cette plaque.
2) Construire l'isobarycentre $I$ des sommets.
A-t-on $G=I$ ?
3) Construire le point d'intersection $K$ des diagonales du trapèze.
A-t-on $G=K$ ?
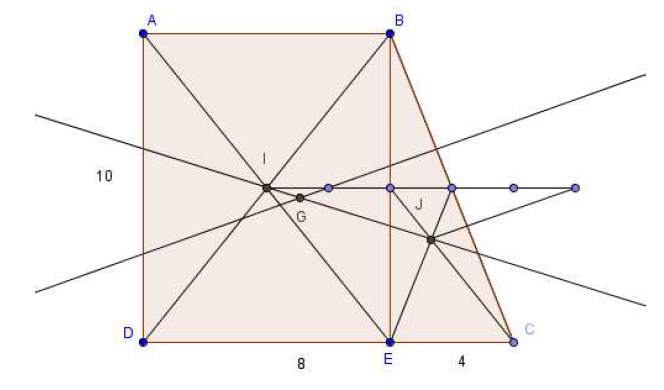
Construisons le centre $I$ du carré $ABED$ et le centre de gravité $J$ du triangle $BEC.$
$G$ est le barycentre de ${(I\;,\ 80)\ ;\ (J\;,\ 20)}$, soit d'après la propriété d'homogénéité, celui de ${(I\;,\ 4)\ ;\ (J\;,\ 1)}$
On a donc $\overrightarrow{IG}=\dfrac{1}{5}\overrightarrow{IJ}.$ (Voir figure ci-dessous).
Soit $F$ le centre de gravité de $ABD.$
Alors $K$ est le barycentre de ${(F\;,\ 3)\ ;\ (C\;,\ 1)}.$
On vérifie sur la figure que $G$ est distinct de $I$ et $K.$
V. Géométrie analytique (droites et repères)
Une base du plan est un couple $(\vec{u}\;,\ \vec{v})$ de vecteurs non colinéaires.
Le triplet $(O\;,\ \vec{u}\;,\ \vec{v})$ où $O$ est un point du plan et $(\vec{u}\;,\ \vec{v})$ une base est un repère cartésien du plan.
Soit $(\vec{i}\;,\ \vec{j})$ une base du plan.
Soit $\vec{u}$ un vecteur quelconque.
Il existe un couple unique $(x\;,\ y)$ de réels tels que :
$\vec{u}=x\vec{i}+y\vec{j}.$
Ces réels $x$ et $y$ sont appelés coordonnées de $\vec{u}$ dans la base $(\vec{i}\;,\ \vec{j}).$
Soit $(O\;,\ \vec{i}\;,\ \vec{j})$ un repère du plan.
Soit $M$ un point quelconque.
Il existe un couple unique $(x\;,\ y)$ de réels tels que :
$\overrightarrow{OM}=x\vec{i}+y\vec{j}.$
Ces réels $x$ et $y$ sont appelés coordonnées de $M$ dans le repère $(O\;,\ \vec{i}\;,\ \vec{j}).$
Condition de colinéarité :
Soit $\vec{u}(x\;,\ y)$ et $\vec{v}(x'\;,\ y')$ dans une base $(\vec{i}\;,\ \vec{j}).$
Alors $\vec{u}$ et $\vec{v}$ sont colinéaires si et seulement si $xy'-yx'=0$ $\ (\Leftrightarrow$ dét$(\vec{u}\;,\ \vec{v})=0).$
Soit dans le plan $\mathcal{P}$ muni du repère $(O\;,\ \vec{i}\;,\ \vec{j})$ les points $A\left(x_{A}\;,\ y_{A}\right)$ et $B\left(x_{B}\;,\ y_{B}\right).$
Alors $\overrightarrow{AB}$ a pour coordonnées $\overrightarrow{AB}\left(x_{B}-x_{A}\;,\ y_{B}-y_{A}\right)$ et le milieu $I$ du segment $[AB]$ a pour coordonnées $I\left(\dfrac{x_{A}+x_{B}}{2}\;;\ \dfrac{y_{A}+y_{B}}{2}\right).$
Représentations analytique d'une droite
Soit $(O\;,\ \vec{i}\;,\ \vec{j})$ un repère du plan.
Soit $\mathcal{D}$ la droite passant par $A(x_{0}\;;\ y_{0})$ et de vecteur directeur $\overrightarrow{u}(\alpha\;,\ \beta).$
Un point $M(x\;,\ y)$ appartient à $\mathcal{D}$ si et seulement si $\overrightarrow{AM}$ et $\overrightarrow{u}$ sont colinéaires , c'est-à-dire s'il existe un réel $t$ tel que :
$\overrightarrow{AM}=t\overrightarrow{AB}$, ce qui se traduit par le système suivant :
$$\left\lbrace\begin{array}{lcl} x&=&x_{A}+t\alpha\\ \\ y&=&y_{A}+t\beta \end{array}\right.$$
appelé système d'équations paramétriques de la droite $\mathcal{D}.$
Soit $\mathcal{D}$ la droite passant par deux points $A$ et $B.$
Un point $M(x\;,\ y)$ appartient à $\mathcal{D}$ si et seulement si $\overrightarrow{AM}$ et $\overrightarrow{AB}$ sont colinéaires, ce qui équivaut à dét $ \left(\overrightarrow{AM}\;,\ \overrightarrow{AB}\right)=0$ et se traduit par une relation de la forme :
$ax+by+c=0$ appelé équation cartésienne de la droite $\mathcal{D}.$
Si $b\neq 0$, cette équation peut se mettre sous la forme $y=mx+p$ et s'appelle alors équation réduite de la droite $\mathcal{D}$ :
$m$ s'appelle le coefficient directeur de $\mathcal{D}$ (si le repère $(O\;,\ \vec{i}\;,\ \vec{j})$ est orthogonal, $m$ est aussi appelé pente de la droite $\mathcal{D}).$
$p$ est l'ordonnée à l'origine.
Coordonnées d'un vecteur directeur de $\mathcal{D}$ :
$\bullet\ $ équation cartésienne $ax+by+c=0$ : $\overrightarrow{u}(-b\;;\ a).$
$\bullet\ $ système d'équations paramétriques $$\left\lbrace\begin{array}{lcl} x&=&x_{A}+t\alpha\\ \\ y&=&y_{A}+t\beta \end{array}\qquad \vec{u}(\alpha\;,\ \beta)\right.$$
$\bullet\ $ équation réduite $y=mx+p$ : $\ \vec{u}(1\;,\ m).$
Conditions de parallélisme
$\left.\begin{array}{lcl} \mathcal{D}\ :\ ax+by+c&=&0\\ \mathcal{D'}\ :\ a'x+b'y+c'&=&0 \end{array}\right\rbrace\qquad\mathcal{D}-\mathcal{D'}\Leftrightarrow ab'-ba'=0$
$\left.\begin{array}{lcl} \mathcal{D}\ :\ y&=&mx+p\\ \mathcal{D'}\ :\ y&=&m'x+p' \end{array}\right\rbrace\qquad\mathcal{D}\times\mathcal{D'}\Leftrightarrow m=m'$

Commentaires
Abdourahmane Diouf (non vérifié)
lun, 11/28/2022 - 07:49
Permalien
La réussite
Ajouter un commentaire