Corrigé Concours d'entrée lycée d'excellence de Diourbel - Épreuve de Mathématiques - 2022

 

$\begin{array}{rcl} 1/\quad x^{2}-y^{2}&=&\left(\dfrac{\sqrt{m}+\sqrt{n}}{2}\right)^{2}-\left(\dfrac{\sqrt{m}-\sqrt{n}}{2}\right)^{2}\\&=&\dfrac{\require{cancel}\cancel{m}+2\sqrt{mn}+\require{cancel}\cancel{n}-\left(\require{cancel}\cancel{m}-2\sqrt{mn}+\require{cancel}\cancel{n}\right)}{4}\\&=&\dfrac{4\sqrt{mn}}{4}\\&=&\boxed{\sqrt{mn}} \end{array}$

 

2/ La condition de colinéarité s'écrit :

 

$|x-1|-4=0$, soit $x-1=4$ ou $x-1=-4$

 

Cela donne $x=5$ ou $\boxed{x=-3}$

 

3. Le système n'admet pas une unique solution si et seulement si

 

$\alpha\times 2-\beta\times(-1)=0$, soit $2\alpha+\beta=0$

 

Cette condition est vérifiée par les réponses $A$ et $D$

 

4/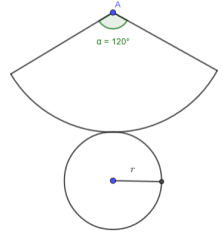 

 

 

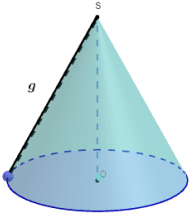
Une formule du cours dit que :

 

$\begin{array}{rcl} \alpha&=&\dfrac{r\times 360^{\circ}}{g}\\\Longrightarrow 120^{\circ}&=&\dfrac{r\times 360^{\circ}}{g}\\\Longrightarrow 120\,g&=&r\times360\\\Longrightarrow\,g&=&3r\\\text{Par ailleurs, on a : }g^{2}&=&h^{2}+r^{2}\\\Longrightarrow\,h&=&\sqrt{g^{2}-r^{2}}\\&=&\sqrt{9r^{2}-r^{2}}\\&=&\sqrt{8r^{2}}\\&=&2\sqrt{2r}\\\text{D'où : }V&=&\dfrac{\pi r^{2}h}{3}\\&=&\boxed{\dfrac{2\sqrt{2\pi r^{3}}}{3}} \end{array}$

 

 

5/  La racine carrée de $3-2\sqrt{2}$ est $\sqrt{2}-1$ car $\left(\sqrt{2}-1\right)^{2}=3-2\sqrt{2}$ et $\sqrt{2}-1$ est positif $\text{puisque }\left(\sqrt{2}\right)^{2}=2\text{ et }1^{2}=1\text{ et }2>1$

 

L'inverse de cette racine carrée est $\dfrac{1}{\sqrt{2}-1}=\dfrac{\sqrt{2}+1}{2-1}=\sqrt{2}+1$

 

Le carré de l'inverse de cette racine carrée est $\left(\sqrt{2}+1\right)^{2}=3+2\sqrt{2}.$ Ce nombre étant positif, sa valeur absolue est aussi $\boxed{3+2\sqrt{2}}$

 

6/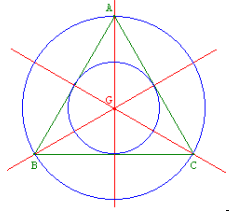 

 

Rappelons que dans un triangle équilatéral, toute hauteur est en même temps médiane et médiatrice. En examinant la figure, on

voit que le rayon du cercle inscrit dans un triangle équilatéral est le tiers de la hauteur issue de A. Il est bien connu que que la hauteur d'un triangle équilatéral de côté $\alpha$ est $\dfrac{a\sqrt{3}}{2}$. Le rayon cherché est donc $\boxed{\dfrac{a\sqrt{3}}{6}}$

 

7/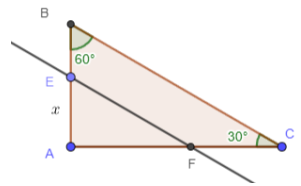

 

$\begin{array}{rcl} \cos 60^{\circ}&=&\dfrac{AB}{BC}\\\Longrightarrow AB&=&BC\times\cos60^{\circ}\\&=&BC\times\dfrac{1}{2}\\&=&10\times\dfrac{1}{2}\\&=&5\\ \text{PAR THALES, }\dfrac{x}{AB}&=&\dfrac{EF}{BC}\\\Longrightarrow\,EF&=&\dfrac{BC}{AB}x\\&=&\boxed{2x} \end{array}$

 

8/ $[(\alpha-1)-2\sqrt{6}][(\alpha-1)+2\sqrt{6}]=(\alpha-1)^{2}-24$

 

Cette expression est égale à $1$ si et seulement si : 

 

$(\alpha-1)^{2}=25$, soit $\alpha-1=5$ ou $\alpha-1=-5$ ou encore $\alpha=6$ ou $\alpha=-4$

 

9./Les équations des deux droites s'écrivent, sous forme réduite :

 

$y=(n-1)x-3$ et $y=-2x+\dfrac{n}{3}$

 

Elles sont perpendiculaires si et seulement si : $-2(n-1)=-1$, soit n=\dfrac{3}{2}=\boxed{1.5}$

 

10/ Le volume initial du pavé droit est : $15\times 12\times 8=1440\,cm^{3}$

 

Sa nouvelle longueur est

 

$\begin{array}{rcl} 15\left(1+\dfrac{25}{100}\right)&=&\dfrac{5}{4}\times 15\\&=&\boxed{\dfrac{75}{4}cm} \end{array}$

 

Sa nouvelle longueur est 

 

$\begin{array}{rcl} 12\left(1+\dfrac{20}{100}\right)&=&\dfrac{6}{5}\times12\\&=&\boxed{\dfrac{72}{5}cm} \end{array}$

 

Sa nouvelle hauteur est 

 

$\begin{array}{rcl} 8\left(1-\dfrac{15}{100}\right)&=&\dfrac{6}{5}\times12\\&=&\boxed{\dfrac{34}{5}cm} \end{array}$

 

Son nouveau volume est, par conséquent : 

 

$\dfrac{75}{4}\times\dfrac{72}{5}\times\dfrac{34}{5}=\boxed{1836\,cm^{3}}$

 

L'augmentation en pourcentage est le nombre $t$ tel que :

 

$\begin{array}{rcl} 1440\left(1+\dfrac{t}{100}\right)&=&1836\\\Longrightarrow\,1+\dfrac{t}{100}&=&\dfrac{1836}{1440}\\\Longrightarrow\,t &=&\dfrac{100\times 396}{1440}\\&=&\boxed{27.5\%} \end{array}$