Corrigé devoir n° 1 maths - 3e
Classe:
Troisième
Exercice 1
Écrivons les expressions suivantes sous la forme $x\sqrt{a}+y\sqrt{b}$ où $x\ $ et $\ y$ sont des réels et $a\ $ et $\ b$ des entiers naturels :
$\begin{array}{rcl} A&=&\sqrt{\dfrac{1}{2}}+(\sqrt{2})^{3}-7\sqrt{3}+\sqrt{72}+\sqrt{\dfrac{81}{3}}\\\\&=&\dfrac{\sqrt{1}}{\sqrt{2}}+(\sqrt{2})^{2}\times(\sqrt{2})-7\sqrt{3}+\sqrt{36\times 2}+\sqrt{27}\\\\&=&\dfrac{1}{\sqrt{2}}+2\times\sqrt{2}-7\sqrt{3}+\sqrt{36}\times\sqrt{2}+\sqrt{9\times 3}\\\\&=&\dfrac{\sqrt{2}}{\sqrt{2}\times\sqrt{2}}+2\sqrt{2}-7\sqrt{3}+6\times\sqrt{2}+\sqrt{9}\times\sqrt{3}\\\\&=&\dfrac{\sqrt{2}}{2}+2\sqrt{2}+6\sqrt{2}-7\sqrt{3}+\sqrt{9}\times\sqrt{3}\\\\&=&\dfrac{\sqrt{2}}{2}+8\sqrt{2}-7\sqrt{3}+3\times\sqrt{3}\\\\&=&\dfrac{\sqrt{2}+16\sqrt{2}}{2}-7\sqrt{3}+3\sqrt{3}\\\\&=&\dfrac{17\sqrt{2}}{2}-4\sqrt{3}\\\\&=&\dfrac{17}{2}\sqrt{2}-4\sqrt{3}\end{array}$
Ainsi, $\boxed{A=\dfrac{17}{2}\sqrt{2}-4\sqrt{3}}$
$\begin{array}{rcl} B&=&\sqrt{200}-5\sqrt{\dfrac{75}{2}}+\dfrac{3}{2}\sqrt{54}-\sqrt{32}\\\\&=&\sqrt{100\times 2}-5\times\dfrac{\sqrt{75}}{\sqrt{2}}+\dfrac{3}{2}\sqrt{9\times 6}-\sqrt{16\times 2}\\\\&=&\sqrt{100}\times\sqrt{2}-5\times\dfrac{\sqrt{25\times 3}}{\sqrt{2}}+\dfrac{3}{2}\times\sqrt{9}\times\sqrt{6}-\sqrt{16}\times\sqrt{2}\\\\&=&10\times\sqrt{2}-5\times\dfrac{\sqrt{25}\times\sqrt{3}}{\sqrt{2}}+\dfrac{3}{2}\times 3\times\sqrt{6}-4\times\sqrt{2}\\\\&=&10\sqrt{2}-5\times\dfrac{5\times\sqrt{3}\times\sqrt{2}}{\sqrt{2}\times\sqrt{2}}+\dfrac{9}{2}\sqrt{6}-4\sqrt{2}\\\\&=&10\sqrt{2}-4\sqrt{2}-25\times\dfrac{\sqrt{3\times 2}}{2}+\dfrac{9}{2}\sqrt{6}\\\\&=&6\sqrt{2}-\dfrac{25}{2}\sqrt{6}+\dfrac{9}{2}\sqrt{6}\\\\&=&6\sqrt{2}-\dfrac{16}{2}\sqrt{6}\\\\&=&6\sqrt{2}-8\sqrt{6}\end{array}$
D'où, $\boxed{B=6\sqrt{2}-8\sqrt{6}}$
$\begin{array}{rcl} C&=&5\sqrt{20}+\dfrac{3}{2}\sqrt{\dfrac{9}{5}}-2\sqrt{343}+10\sqrt{28}\\\\&=&5\sqrt{4\times 5}+\dfrac{3}{2}\times\dfrac{\sqrt{9}}{\sqrt{5}}-2\sqrt{49\times 7}+10\sqrt{4\times 7}\\\\&=&5\times\sqrt{4}\times\sqrt{5}+\dfrac{3}{2}\times\dfrac{3}{\sqrt{5}}-2\times\sqrt{49}\times\sqrt{7}+10\times\sqrt{4}\times\sqrt{7}\\\\&=&5\times 2\times\sqrt{5}+\dfrac{3}{2}\times\dfrac{3\times\sqrt{5}}{\sqrt{5}\times\sqrt{5}}-2\times 7\times\sqrt{7}+10\times 2\times\sqrt{7}\\\\&=&10\sqrt{5}+\dfrac{3}{2}\times\dfrac{3\times\sqrt{5}}{5}-14\sqrt{7}+20\sqrt{7}\\\\&=&10\sqrt{5}+\dfrac{9\sqrt{5}}{10}+6\sqrt{7}\\\\&=&\dfrac{100\sqrt{5}}{10}+\dfrac{9\sqrt{5}}{10}+6\sqrt{7}\\\\&=&\dfrac{109\sqrt{5}}{10}+6\sqrt{7}\end{array}$
Donc, $\boxed{C=\dfrac{109}{10}\sqrt{5}+6\sqrt{7}}$
Exercice 2
Calculons les expressions suivantes tout en rendant rationnel le dénominateur :
$\begin{array}{rcl} X&=&\dfrac{3\sqrt{2}-4\sqrt{5}}{\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{2}}{3}}\\\\&=&\dfrac{3\sqrt{2}-4\sqrt{5}}{\dfrac{3\sqrt{3}}{6}-\dfrac{2\sqrt{2}}{6}}\\\\&=&\dfrac{3\sqrt{2}-4\sqrt{5}}{\dfrac{3\sqrt{3}-2\sqrt{2}}{6}}\\\\&=&\dfrac{6\times(3\sqrt{2}-4\sqrt{5})}{3\sqrt{3}-2\sqrt{2}}\\\\&=&\dfrac{6\times(3\sqrt{2}-4\sqrt{5})\times(3\sqrt{3}+2\sqrt{2})}{(3\sqrt{3}-2\sqrt{2})(3\sqrt{3}+2\sqrt{2})}\\\\&=&\dfrac{6\times[(3\sqrt{2})\times(3\sqrt{3})+(3\sqrt{2})\times(2\sqrt{2})-(4\sqrt{5})\times(3\sqrt{3})-(4\sqrt{5})\times(2\sqrt{2})]}{(3\sqrt{3})^{2}-(2\sqrt{2})^{2}}\\\\&=&\dfrac{6\times[(9\sqrt{2}\times\sqrt{3})+(6\sqrt{2}\times\sqrt{2})-(12\sqrt{5}\times\sqrt{3})-(8\sqrt{5}\times\sqrt{2})]}{(9\times 3)-(4\times 2)}\\\\&=&\dfrac{6\times(9\sqrt{6}+12-12\sqrt{15}-8\sqrt{10})}{27-8}\\\\&=&\dfrac{6\times(9\sqrt{6}+12-12\sqrt{15}-8\sqrt{10})}{19}\\\\&=&\dfrac{54\sqrt{6}-72\sqrt{15}-48\sqrt{10}+72}{19}\end{array}$
Ainsi, $\boxed{X=\dfrac{54\sqrt{6}-72\sqrt{15}-48\sqrt{10}+72}{19}}$
$\begin{array}{rcl} Y&=&\dfrac{2\sqrt{3}+3\sqrt{2}}{-2\sqrt{3}-3\sqrt{2}}\\\\&=&\dfrac{2\sqrt{3}+3\sqrt{2}}{-(2\sqrt{3}+3\sqrt{2})}\\\\&=&-\dfrac{2\sqrt{3}+3\sqrt{2}}{2\sqrt{3}+3\sqrt{2}}\\\\&=&-1\end{array}$
D'où, $\boxed{Y=-1}$
$\begin{array}{rcl} Z&=&\dfrac{\sqrt{7}-\sqrt{5}}{\sqrt{\dfrac{2}{3}}}\\\\&=&\dfrac{\sqrt{7}-\sqrt{5}}{\dfrac{\sqrt{2}}{\sqrt{3}}}\\\\&=&\dfrac{(\sqrt{7}-\sqrt{5})\times\sqrt{3}}{\sqrt{2}}\\\\&=&\dfrac{(\sqrt{7}-\sqrt{5})\times\sqrt{3}\times\sqrt{2}}{\sqrt{2}\times\sqrt{2}}\\\\&=&\dfrac{(\sqrt{7}-\sqrt{5})\times\sqrt{6}}{2}\\\\&=&\dfrac{\sqrt{6}(\sqrt{7}-\sqrt{5})}{2}\end{array}$
D'où, $\boxed{Z=\dfrac{\sqrt{6}(\sqrt{7}-\sqrt{5})}{2}}$
$\begin{array}{rcl} T&=&\dfrac{\dfrac{2\sqrt{5}-3\sqrt{11}}{4\sqrt{3}+\sqrt{7}}}{\sqrt{\dfrac{3}{2}}}\\\\&=&\dfrac{\dfrac{2\sqrt{5}-3\sqrt{11}}{4\sqrt{3}+\sqrt{7}}}{\dfrac{\sqrt{3}}{\sqrt{2}}}\\\\&=&\dfrac{2\sqrt{5}-3\sqrt{11}}{4\sqrt{3}+\sqrt{7}}\times\dfrac{\sqrt{2}}{\sqrt{3}}\\\\&=&\dfrac{(2\sqrt{5}-3\sqrt{11})\times\sqrt{2}}{(4\sqrt{3}+\sqrt{7})\times\sqrt{3}}\\\\&=&\dfrac{2\sqrt{5}\times\sqrt{2}-3\sqrt{11}\times\sqrt{2}}{4\sqrt{3}\times\sqrt{3}+\sqrt{7}\times\sqrt{3}}\\\\&=&\dfrac{2\sqrt{10}-3\sqrt{22}}{12+\sqrt{21}}\\\\&=&\dfrac{(2\sqrt{10}-3\sqrt{22})(12-\sqrt{21})}{(12+\sqrt{21})(12-\sqrt{21})}\\\\&=&\dfrac{24\sqrt{10}-36\sqrt{22}-2\sqrt{10}\times\sqrt{21}+3\sqrt{22}\times\sqrt{21}}{(12)^{2}-(\sqrt{21})^{2}}\\\\&=&\dfrac{24\sqrt{10}-36\sqrt{22}-2\sqrt{210}+3\sqrt{462}}{144-21}\\\\&=&\dfrac{24\sqrt{10}-36\sqrt{22}-2\sqrt{210}+3\sqrt{462}}{123}\end{array}$
Ainsi, $\boxed{T=\dfrac{24\sqrt{10}-36\sqrt{22}-2\sqrt{210}+3\sqrt{462}}{123}}$
Exercice 3
Soit un réel $a\ $ tel que : $a=1+\sqrt{\dfrac{1}{2}}$ et soit $b$ son expression conjuguée.
1) Déterminer $b$
Comme $b$ est l'expression conjuguée de $a$ alors, on a :
$$b=1-\sqrt{\dfrac{1}{2}}=1-\dfrac{\sqrt{2}}{2}$$
Calculons $(a+b)^{2}$
On a :
$\begin{array}{rcl} (a+b)^{2}&=&\left(1+\sqrt{\dfrac{1}{2}}+1-\sqrt{\dfrac{1}{2}}\right)^{2}\\\\&=&(2)^{2}\\\\&=&4\end{array}$
Ainsi, $\boxed{(a+b)^{2}=4}$
2) Montrons que $2ab=1$
En calculant $a\times b$, on obtient :
$\begin{array}{rcl} a\times b&=&\left(1+\sqrt{\dfrac{1}{2}}\right)\left(1-\sqrt{\dfrac{1}{2}}\right)\\\\&=&(1)^{2}-\left(\sqrt{\dfrac{1}{2}}\right)^{2}\\\\&=&1-\dfrac{1}{2}\\\\&=&\dfrac{1}{2}\end{array}$
Par suite $2ab=2\times\dfrac{1}{2}=1$
D'où, $\boxed{2ab=1}$
Déduisons alors l'expression de $a^{2}+b^{2}$
On sait que : $(a+b)^{2}=a^{2}+b^{2}+2ab$
Donc, $a^{2}+b^{2}=(a+b)^{2}-2ab$
Ce qui donne : $a^{2}+b^{2}=4-1=3$
Ainsi, $\boxed{a^{2}+b^{2}=3}$
Exercice 4
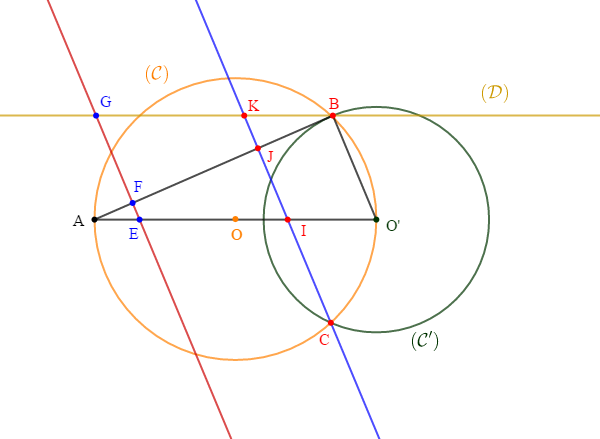
On considère deux cercle $\mathcal{C}(O\;,\ 2.5)\ $ et $\ \mathcal{C}'(O'\;,\ 2)$ sécantes en $B\ $ et $\ C.$
Soit $\mathcal{(D)}$ la droite passant par $B$ et parallèle à $(AO).$
La droite passant par $C$ et parallèle à la droite $(O'B)$ coupe $(OA)$ en $I\;,\ (AB)$ en $J$ et $(\mathcal{D})$ en $K.$ On donne $O'I=1.6$

1) Calculons $AB\;;\ BK\ $ et $\ BJ$
$-\ $ Calcul de $AB$
Le triangle $ABO'$ est inscrit sur le cercle $(\mathcal{C})$ tel que $[AO']$ est un diamètre de $(\mathcal{C}).$
Alors, $ABO'$ est un triangle rectangle en $B.$
Donc, en appliquant le théorème de Pythagore, on a :
$$AO'^{2}=AB^{2}+O'B^{2}$$
Par suite, $AB^{2}=AO'^{2}-O'B^{2}$ avec $AO'=2\times 2.5=5\;cm$
Comme $B\in(\mathcal{C}')$ alors, $O'B=2\;cm$
Ainsi,
$\begin{array}{rcl} AB&=&\sqrt{AO'^{2}-O'B^{2}}\\\\&=&\sqrt{5^{2}-2^{2}}\\\\&=&\sqrt{25-4}\\\\&=&\sqrt{21}\end{array}$
D'où, $\boxed{AB=\sqrt{21}\;cm}$
$-\ $ Calcul de $BK$
On a : $(IK)$ parallèle à $(O'B)\ $ et $\ (BK)$ parallèle à $(O'I)$ alors, $IO'BK$ est un parallélogramme.
D'où, $BK=O'I$
Par conséquent, $\boxed{BK=1.6\;cm}$
$-\ $ Calcul de $BJ$
Comme les droites $(IJ)\ $ et $\ (O'B)$ sont parallèles alors, les triangles $ABO'\ $ et $\ AIJ$ sont en position de Thalès.
Donc, en appliquant une conséquence du théorème de Thalès, on obtient :
$$\dfrac{BJ}{AB}=\dfrac{O'I}{AO'}$$
Par suite,
$\begin{array}{rcl} BJ&=&\dfrac{O'I}{AO'}\times AB\\\\&=&\dfrac{1.6}{5}\times\sqrt{21}\\\\&=&\dfrac{1.6\sqrt{21}}{5}\end{array}$
D'où, $\boxed{BJ=\dfrac{1.6\sqrt{21}}{5}\;cm}$
2) Soit $E\in[AO]\ $ et $\ F\in[AJ]$ tels que :
$$AE=x\quad\text{et}\quad AF=\dfrac{x\sqrt{21}}{5}$$
La droite passant par $E\ $ et $\ F$ coupe $(\mathcal{D})$ en $G$
Montrons que $(EG)$ est parallèle à $(O'B)$
D'une part, $A\;;\ F\;;\ B$ sont trois points alignés dans cet ordre et d'autre part, $A\;;\ E\;;\ O'$ sont trois points alignés dans cet ordre.
Alors, on a :
$\begin{array}{rcl}\dfrac{AF}{AB}&=&\dfrac{\dfrac{x\sqrt{21}}{5}}{\sqrt{21}}\\\\&=&\dfrac{x\sqrt{21}}{5}\times\dfrac{1}{\sqrt{21}}\\\\&=&\dfrac{x}{5}\end{array}$
Donc, $\boxed{\dfrac{AF}{AB}=\dfrac{x}{5}}$
Aussi, on a : $\boxed{\dfrac{AE}{AO'}=\dfrac{x}{5}}$
Ainsi, on constate que :
$$\dfrac{AF}{AB}=\dfrac{AE}{AO'}=\dfrac{x}{5}$$
Par suite, d'après la réciproque du théorème de Thalès, les droites $(EF)\ $ et $\ (O'B)$ sont parallèles.
D'où, $(EG)$ est parallèle à $(O'B)$
3) En déduisons que $(EG)$ est parallèle à $(IJ)$
On a : $(IJ)$ parallèle à $(O'B)\ $ et $\ (EG)$ parallèle à $(O'B)$
Or, si deux droites sont parallèles alors, toute droite parallèle à l'une est aussi parallèle à l'autre.
Donc, $(EG)$ est bien parallèle à $(IJ).$
Auteur:
Diny Faye

Commentaires
Anonyme (non vérifié)
sam, 11/13/2021 - 17:34
Permalien
Merci beaucoup
Anonyme (non vérifié)
dim, 12/18/2022 - 23:30
Permalien
je vous remercie merci
Abdou salam Diane (non vérifié)
lun, 10/16/2023 - 23:11
Permalien
BFM
Abdou salam Diane (non vérifié)
lun, 10/16/2023 - 23:11
Permalien
BFM
Oumy Faye ❤ (non vérifié)
ven, 10/18/2024 - 18:41
Permalien
Je veux réussir mes examens
Anonyme (non vérifié)
mer, 10/18/2023 - 17:40
Permalien
Merci de votre fidélité et
Mame Adama dieng (non vérifié)
mar, 11/07/2023 - 22:05
Permalien
Merci infiniment
Dieynaba (non vérifié)
sam, 11/11/2023 - 01:40
Permalien
J’ai pas compris car vos
Oumy Faye ❤ (non vérifié)
ven, 10/18/2024 - 18:40
Permalien
Je veux apprendre dans cette
Mame Diarra Ndiaye (non vérifié)
dim, 11/03/2024 - 18:52
Permalien
Je vous remercie
Serigne cheikh (non vérifié)
ven, 10/31/2025 - 22:03
Permalien
Le correction des exercices
Ajouter un commentaire