Corrigé devoir n° 2 maths - 5e
Classe:
Cinquième
Exercice 1
On considère la figure ci-dessous où le triangle $KLM$ est rectangle isocèle en $M.$
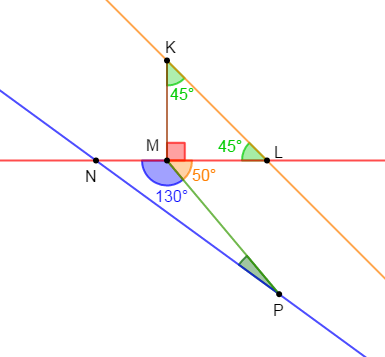
1) Déterminons par mesure $\widehat{NMP}$
Avec un rapporteur, on mesure l'angle $\widehat{NMP}.$
Ce qui donne : $\boxed{\widehat{NMP}=130^{\circ}}$
2) $(KL)\ $ et $\ (MP)$ ne sont pas parallèles.
Justifions notre réponse
En effet, $(KL)\ $ et $\ (MP)$ sont deux droites coupées par la sécante $(ML)$ donc, les angles $\widehat{KLM}\ $ et $\ \widehat{LMP}$ sont alternes internes.
Or, $KLM$ est rectangle isocèle en $M.$
Donc, $\widehat{KLM}=45^{\circ}$
Aussi, $\widehat{NMP}\ $ et $\ \widehat{LMP}$ sont adjacents supplémentaires donc, $\widehat{NMP}+\widehat{LMP}=180^{\circ}.$
Par suite,
$\begin{array}{rcl}\widehat{LMP}&=&180^{\circ}-\widehat{NMP}\\\\&=&180^{\circ}-130^{\circ}\\\\&=&50^{\circ}\end{array}$
Donc, $\widehat{LMP}=50^{\circ}$
Ainsi, on constate que les angles $\widehat{KLM}\ $ et $\ \widehat{LMP}$ alternes internes n'ont pas la même mesure.
Par conséquent, les droites $(KL)\ $ et $\ (MP)$ ne sont pas parallèles.
Exercice 2
On donne un segment $[AM].$
1) Construisons le triangle $ABC$ tel que
$$\widehat{ABC}=74^{\circ} \ \text{ et }\ \widehat{ACB}=58^{\circ}$$
$B\ $ et $\ C$ distincts de $M.$
2) Plaçons le point $O$ milieu du segment $[AM].$
3) Construisons les points $N\ $ et $\ P$ symétriques respectifs des points $B\ $ et $\ C$ par rapport au point $O.$
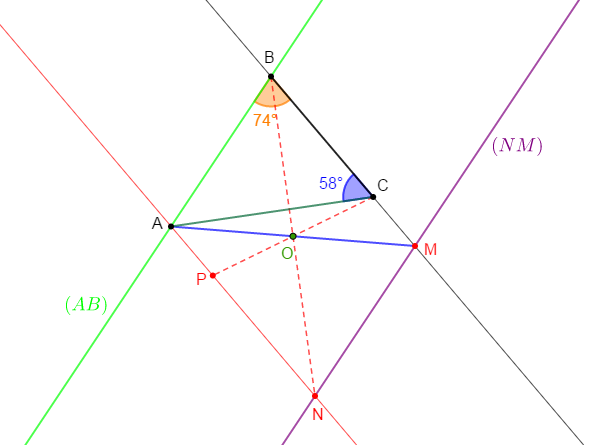
4) Justifions que $M$ est le symétrique du point $A$ par rapport à $O.$
Comme $O$ est le milieu de $[AM]$ alors, les distances $OA\ $ et $\ OM$ sont égales.
D'où, $M$ est le symétrique de $A$ par rapport à $O.$
Remarque :
$A$ est aussi le symétrique de $M$ par rapport à $O.$
On dit que : $M\ $ et $\ A$ sont symétriques par rapport à $O.$
5) Les droites $(AB)\ $ et $\ (NM)$ sont parallèles.
En effet, $S_{_{O}}[A]=M\ $ et $\ S_{_{O}}[B]=N.$
Donc, $(NM)\ $ est le symétrique de $(AB)$ par rapport à $O.$
Or, le symétrique d'une droite par rapport à un point est une droite qui lui est parallèle.
D'où, $(AB)\ $ et $\ (NM)$ sont parallèles.
6) Les points $A\;,\ P\ $ et $\ N$ sont alignés.
Justifions notre réponse.
En effet, on constate que les points $M\;,\ C\ $ et $\ B$ sont alignés.
Or, les symétriques de trois points alignés par rapport à un point sont aussi trois points alignés.
Donc, $A\;,\ P\ $ et $\ N$ symétriques respectifs de $M\;,\ C\ $ et $\ B$ par rapport à $O$ sont alignés.
Exercice 3
1) Calculons en respectant les règles de la prioritaire
$\begin{array}{rcl} A&=&32.5-3\times(4-3)^{3}+3\times(18\div 2-5)\\\\&=&32.5-3\times 1^{3}+3\times(9-5)\\\\&=&32.5-3\times 1+3\times 4\\\\&=&32.5-3+12\\\\&=&41.5\end{array}$
D'où, $\boxed{A=41.5}$
$\begin{array}{rcl} B&=&10.5\times[17-3\times(14-2^{3})]\times 2\\\\&=&10.5\times[17-3\times(14-8)]\times 2\\\\&=&10.5\times[17-3\times 6]\times 2\\\\&=&10.5\times[17-18]\times 2\\\\&=&10.5\times[-1]\times 2\\\\&=&-10.5\times 2\\\\&=&-21\end{array}$
Ainsi, $\boxed{B=-21}$
2) Montrons que
$$8a^{3}\times 27b^{3}=(6ab)^{3}$$
On sait que :
$8=2\times 2\times 2=2^{3}$
$27=3\times 3\times 3=3^{3}$
Donc,
$\begin{array}{rcl} 8a^{3}\times 27b^{3}&=&2^{3}\times a^{3}\times 3^{3}\times b^{3}\\\\&=&(2\times a\times 3\times b)^{3}\\\\&=&(2\times 3\times a\times b)^{3}\\\\&=&(6\times a\times b)^{3}\end{array}$
D'où, $\boxed{8a^{3}\times 27b^{3}=(6ab)^{3}}$
$8a^{3}\times 27b^{3}=2^{3}\times a^{3}\times 3^{3}\times b^{3}$
3) Calculons :
a) $PPCM(180\;;\ 210)$
Décomposons $180\ $ et $\ 210$ en produits de facteurs premiers.
On a :
$\begin{array}{r|l} 180&2\\90&2\\45&3\\15&3\\5&5\\1&\end{array}$ donc, $180=2^{2}\times 3^{2}\times 5$
$\begin{array}{r|l} 210&2\\105&5\\21&3\\7&7\\1&\end{array}$ alors, $210=2\times 3\times 5\times 7$
Par suite,
$\begin{array}{rcl} PPCM(180\;;\ 210)&=&2^{2}\times 3^{2}\times 5\times 7\\\\&=&1\,260\end{array}$
D'où, $\boxed{PPCM(180\;;\ 210)=1\,260}$
b) $PPCM(104\;;\ 240)$
En décomposant $104\ $ et $\ 240$ en produits de facteurs premiers, on obtient :
$\begin{array}{r|l} 104&2\\52&2\\26&2\\13&13\\1&\end{array}$ donc, $104=2^{3}\times 13$
$\begin{array}{r|l} 240&2\\120&2\\60&2\\30&2\\15&3\\5&5\\1&\end{array}$ alors, $240=2^{4}\times 3\times 5$
Par suite,
$\begin{array}{rcl} PPCM(104\;;\ 240)&=&2^{4}\times 3\times 5\times 13\\\\&=&3\,120\end{array}$
Ainsi, $\boxed{PPCM(104\;;\ 240)=3\,120}$
c) $PGCD(225\;;\ 360)$
En décomposant $225\ $ et $\ 360$ en produits de facteurs premiers, on obtient :
$\begin{array}{r|l} 225&5\\45&5\\9&3\\3&3\\1&\end{array}$ alors, $225=3^{2}\times 5^{2}$
$\begin{array}{r|l} 360&2\\180&2\\90&2\\45&3\\15&3\\5&5\\1&\end{array}$ donc, $360=2^{3}\times 3^{2}\times 5$
Par suite,
$\begin{array}{rcl} PGCD(225\;;\ 360)&=&3^{2}\times 5\\\\&=&45\end{array}$
D'où, $\boxed{PGCD(225\;;\ 360)=45}$
Auteur:
Diny Faye

Commentaires
Madame Amina sy (non vérifié)
jeu, 11/14/2024 - 01:23
Permalien
Enseignement
Anonyme (non vérifié)
mar, 11/26/2024 - 14:31
Permalien
Calculer en respectant les règles de priorités
Ajouter un commentaire