Corrigé devoir n° 3 maths - 2nd s

 

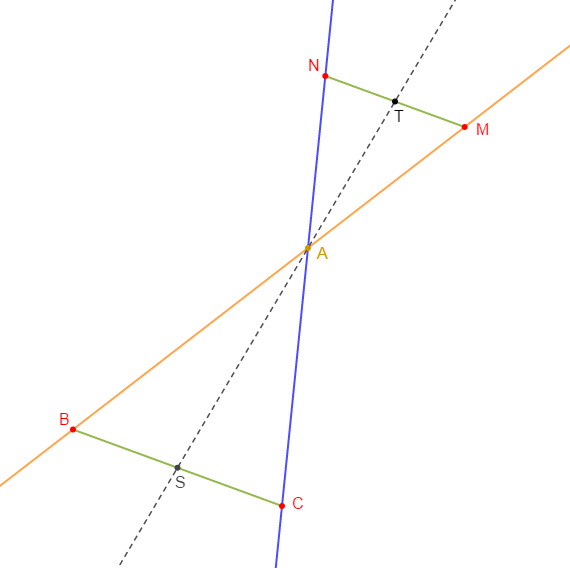
Soit $ABC$ un triangle quelconque.

 

1) Construisons les points $M\ $ et $\ N$ tels que :

 

$$\overrightarrow{AM}=-\dfrac{2}{3}\overrightarrow{AB}\ \text{ et }\ \overrightarrow{AN}=-\dfrac{2}{3}\overrightarrow{AC}$$

 

2) Démontrons que $(MN)\ $ et $\ (BC)$ sont parallèles.

 

D'une part, $M\;;\ A\;;\ B$ sont trois points alignés dans cet ordre et d'autre part, $N\;;\ A\;;\ C$ sont trois points alignés dans cet ordre.

 

De plus, $\dfrac{\|\overrightarrow{AM}\|}{\|\overrightarrow{AB}\|}=\dfrac{2}{3}\ $ et $\ \dfrac{\|\overrightarrow{AN}\|}{\|\overrightarrow{AC}\|}=\dfrac{2}{3}$

 

Par ailleurs, on a :

 

$\begin{array}{rcl} \overrightarrow{AN}-\overrightarrow{AM}=\overrightarrow{MN}&=&-\dfrac{2}{3}\overrightarrow{AC}+\dfrac{2}{3}\overrightarrow{AB}\\\\&=&-\dfrac{2}{3}\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\\\\&=&-\dfrac{2}{3}\left(\overrightarrow{AC}+\overrightarrow{BA}\right)\\\\&=&-\dfrac{2}{3}\overrightarrow{BC}\end{array}$

 

Alors, $\overrightarrow{MN}=-\dfrac{2}{3}\overrightarrow{BC}$

 

Par suite, $\dfrac{\|\overrightarrow{MN}\|}{\|\overrightarrow{BC}\|}=\dfrac{2}{3}$

 

Ainsi,

$$\dfrac{\|\overrightarrow{AM}\|}{\|\overrightarrow{AB}\|}=\dfrac{\|\overrightarrow{AN}\|}{\|\overrightarrow{AC}\|}=\dfrac{\|\overrightarrow{MN}\|}{\|\overrightarrow{BC}\|}$$

Par conséquent, d'après la réciproque du théorème de Thalès, les droites $(MN)\ $ et $\ (BC)$ sont parallèles.

 

3) Soient $S\ $ et $\ T$ les milieux respectifs de $[BC]\ $ et $\ [MN].$ Démontrons que les points $A\;,\ S\ $ et $\ T$ sont alignés.

 

Pour cela, il suffit de montrer que les vecteurs $\overrightarrow{AS}$ et $\overrightarrow{AT}$ sont colinéaires.

 

On a : $\overrightarrow{AM}+\overrightarrow{AN}=-\dfrac{2}{3}\overrightarrow{AB}-\dfrac{2}{3}\overrightarrow{AC}$

 

Alors, en appliquant la relation de Chasles, on obtient :

$$\overrightarrow{AT}+\overrightarrow{TM}+\overrightarrow{AT}+\overrightarrow{TN}=-\dfrac{2}{3}\left(\overrightarrow{AS}+\overrightarrow{SB}\right)-\dfrac{2}{3}\left(\overrightarrow{AS}+\overrightarrow{SC}\right)$$

Ce qui donne : $2\overrightarrow{AT}+\overrightarrow{TM}+\overrightarrow{TN}=-\dfrac{4}{3}\overrightarrow{AS}-\dfrac{2}{3}\left(\overrightarrow{SB}+\overrightarrow{SC}\right)$

 

Or, $S\ $ et $\ T$ milieux respectifs de $[BC]\ $ et $\ [MN]$ donc,

 

$$\overrightarrow{TM}+\overrightarrow{TN}=\vec{0}\ \text{ et }\ \overrightarrow{SB}+\overrightarrow{SC}=\vec{0}$$

 

Par suite, $2\overrightarrow{AS}=-\dfrac{4}{3}\overrightarrow{AT}$

 

D'où, $\boxed{\overrightarrow{AS}=-\dfrac{2}{3}\overrightarrow{AT}}$

 

Ce qui prouve que les points $A\;,\ S\ $ et $\ T$ sont alignés.

 

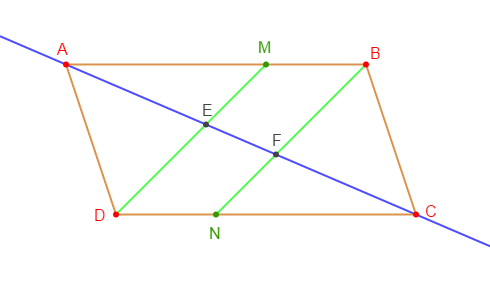
On considère un parallélogramme $ABCD$. Les points $M$ et $N$ sont tels que :

 

$$\overrightarrow{AM}=\dfrac{2}{3}\overrightarrow{AB}\ \text{ et }\ \overrightarrow{CN}=\dfrac{2}{3}\overrightarrow{CD}$$

 

1) Faisons une figure.

 

2) Montrons que $BMDN$ est un parallélogramme.

 

On a :

 

$\begin{array}{rcl}\overrightarrow{AM}+\overrightarrow{CN}&=&\dfrac{2}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{CD}\\\\&=&\dfrac{2}{3}\left(\overrightarrow{AB}+\overrightarrow{CD}\right)\end{array}$

 

Or, $ABCD$ parallélogramme donc, $\overrightarrow{AB}=-\overrightarrow{CD}\ \Rightarrow\ \overrightarrow{AB}+\overrightarrow{CD}=\vec{0}$

 

Par suite,

 

$\begin{array}{rcl}\overrightarrow{AM}+\overrightarrow{CN}=\vec{0}&\Rightarrow&\overrightarrow{AB}+\overrightarrow{BM}+\overrightarrow{CD}+\overrightarrow{DN}=\vec{0}\\\\&\Rightarrow&\underbrace{\overrightarrow{AB}+\overrightarrow{CD}}_{=\vec{0}}+\overrightarrow{BM}+\overrightarrow{DN}=\vec{0}\\\\&\Rightarrow&\overrightarrow{BM}+\overrightarrow{DN}=\vec{0}\\\\&\Rightarrow&\overrightarrow{BM}=\overrightarrow{ND}\end{array}$

 

Ainsi, $\boxed{\overrightarrow{BM}=\overrightarrow{ND}}$

 

Ce qui montre que $BMDN$ est un parallélogramme.

 

3) Soit $E$ le point commun aux droites $(DM)\ $ et $\ (AC).$

 

Soit $F$ le point commun aux droites $(BN)\ $ et $\ (AC).$

 

Déterminons les réels $a\ $ et $\ b$ tels que :

$$\overrightarrow{AE}=a\overrightarrow{AC}\ \text{ et }\ \overrightarrow{AF}=b\overrightarrow{AC}$$

$A\;;\ E\;;\ F\;;\ C$ sont quatre points alignés dans cet ordre.

 

D'après la relation de Chasles, on a :

$$\overrightarrow{AE}+\overrightarrow{EF}+\overrightarrow{FC}=\overrightarrow{AC}$$

Or, les triangles $AFB\ $ et $\ AEM$ étant en position de Thalès alors, d'après le théorème de Thalès, on a :

 

$\begin{array}{rcl}\dfrac{\|\overrightarrow{AF}\|}{\|\overrightarrow{AE}\|}=\dfrac{\|\overrightarrow{AB}\|}{\|\overrightarrow{AM}\|}&\Rightarrow&\dfrac{\|\overrightarrow{AE}\|+\|\overrightarrow{EF}\|}{\|\overrightarrow{AE}\|}=\dfrac{3}{2}\\\\&\Rightarrow&1+\dfrac{\|\overrightarrow{EF}\|}{\|\overrightarrow{AE}\|}=\dfrac{3}{2}\\\\&\Rightarrow&\dfrac{\|\overrightarrow{EF}\|}{\|\overrightarrow{AE}\|}=\dfrac{3}{2}-1\\\\&\Rightarrow&\dfrac{\|\overrightarrow{EF}\|}{\|\overrightarrow{AE}\|}=\dfrac{1}{2}\\\\&\Rightarrow&\|\overrightarrow{EF}\|=\dfrac{1}{2}\|\overrightarrow{AE}\|\end{array}$

 

D'où, $\boxed{\overrightarrow{EF}=\dfrac{1}{2}\overrightarrow{AE}}$

 

De la même manière, en considérant les triangles $CED\ $ et $\ CFN$ qui sont en position de Thalès, on obtient :

 

$\begin{array}{rcl}\dfrac{\|\overrightarrow{EC}\|}{\|\overrightarrow{FC}\|}=\dfrac{\|\overrightarrow{DC}\|}{\|\overrightarrow{NC}\|}&\Rightarrow&\dfrac{\|\overrightarrow{EF}\|+\|\overrightarrow{FC}\|}{\|\overrightarrow{FC}\|}=\dfrac{3}{2}\\\\&\Rightarrow&\dfrac{\|\overrightarrow{EF}\|}{\|\overrightarrow{FC}\|}+1=\dfrac{3}{2}\\\\&\Rightarrow&\dfrac{\|\overrightarrow{EF}\|}{\|\overrightarrow{FC}\|}=\dfrac{3}{2}-1\\\\&\Rightarrow&\dfrac{\|\overrightarrow{EF}\|}{\|\overrightarrow{FC}\|}=\dfrac{1}{2}\\\\&\Rightarrow&\|\overrightarrow{EF}\|=\dfrac{1}{2}\|\overrightarrow{FC}\|\end{array}$

 

Donc, $\boxed{\overrightarrow{EF}=\dfrac{1}{2}\overrightarrow{FC}}$

$$\left\lbrace\begin{array}{rcl}\overrightarrow{EF}&=&\dfrac{1}{2}\overrightarrow{AE}\\\\\overrightarrow{EF}&=&\dfrac{1}{2}\overrightarrow{FC}\end{array}\right.\ \Rightarrow\ \overrightarrow{AE}=\overrightarrow{FC}$$

Ainsi,

 

$\begin{array}{rcl}\overrightarrow{AE}+\overrightarrow{EF}+\overrightarrow{FC}=\overrightarrow{AC}&\Rightarrow&\overrightarrow{AE}+\dfrac{1}{2}\overrightarrow{AE}+\overrightarrow{AE}=\overrightarrow{AC}\\\\&\Rightarrow&\left(1+\dfrac{1}{2}+1\right)\overrightarrow{AE}=\overrightarrow{AC}\\\\&\Rightarrow&\dfrac{5}{2}\overrightarrow{AE}=\overrightarrow{AC}\\\\&\Rightarrow&\overrightarrow{AE}=\dfrac{2}{5}\overrightarrow{AC}\end{array}$

 

D'où, $\boxed{\overrightarrow{AE}=\dfrac{2}{5}\overrightarrow{AC}}$

 

Par ailleurs, d'après Thalès, on a : $\overrightarrow{AE}=\dfrac{2}{3}\overrightarrow{AF}$

 

Donc,

 

$\begin{array}{rcl}\overrightarrow{AF}&=&\dfrac{3}{2}\overrightarrow{AE}\\\\&=&\dfrac{3}{2}\times\dfrac{2}{5}\overrightarrow{AC}\\\\&=&\dfrac{3}{5}\overrightarrow{AC}\end{array}$

 

D'où, $\boxed{\overrightarrow{AF}=\dfrac{3}{5}\overrightarrow{AC}}$

 

On peut aussi utiliser la relation de Chasles :

 

$\begin{array}{rcl}\overrightarrow{AF}&=&\overrightarrow{AE}+\overrightarrow{EF}\\\\&=&\overrightarrow{AE}+\dfrac{1}{2}\overrightarrow{AE}\\\\&=&\dfrac{3}{2}\overrightarrow{AE}\\\\&=&\dfrac{3}{2}\times\dfrac{2}{5}\overrightarrow{AC}\\\\&=&\dfrac{3}{5}\overrightarrow{AC}\end{array}$

 

Ainsi, $\boxed{\overrightarrow{AF}=\dfrac{3}{5}\overrightarrow{AC}}$

 

Soit $ABC$ un triangle et un nombre $x.$ A chaque valeur de $x$, on associe les points $E$ et $F$ tels que :

 

$$\overrightarrow{AE}=\dfrac{1}{3}\overrightarrow{AB}+x\overrightarrow{AC}\ \text{ et }\ \overrightarrow{AF}=x\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}$$

 

1) Faisons une figure lorsque $x=-\dfrac{1}{2}.$

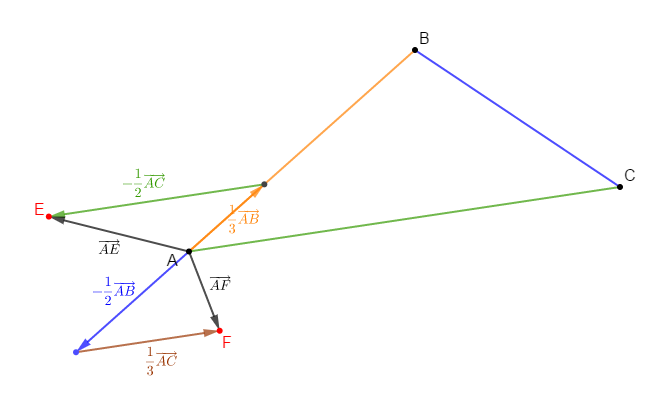
En effet, pour $x=-\dfrac{1}{2}$, on a :

$$\overrightarrow{AE}=\dfrac{1}{3}\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AC}\ \text{ et }\ \overrightarrow{AF}=-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}$$

Donc, en considérant le repère $(A\;;\ \overrightarrow{AB}\;;\ \overrightarrow{AC})$, on place les points $E\ $ et $\ F.$

 

2) Démontrons que, quel que soit le nombre $x$, les vecteurs $\overrightarrow{EF}\ $ et $\ \overrightarrow{BC}$ sont colinéaires.

 

En effet, d'après la relation de Chasles, on a :

 

$\begin{array}{rcl}\overrightarrow{EF}&=&\overrightarrow{EA}+\overrightarrow{AF}\\\\&=&-\dfrac{1}{3}\overrightarrow{AB}-x\overrightarrow{AC}+x\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\\\\&=&\dfrac{1}{3}\left(\overrightarrow{AC}-\overrightarrow{AB}\right)+x\left(\overrightarrow{AB}-\overrightarrow{AC}\right)\\\\&=&\dfrac{1}{3}\left(\overrightarrow{AC}+\overrightarrow{BA}\right)+x\left(\overrightarrow{AB}+\overrightarrow{CA}\right)\\\\&=&\dfrac{1}{3}\overrightarrow{BC}+x\overrightarrow{CB}\\\\&=&\dfrac{1}{3}\overrightarrow{BC}-x\overrightarrow{BC}\\\\&=&\left(\dfrac{1}{3}-x\right)\overrightarrow{BC}\end{array}$

 

D'où, $\boxed{\overrightarrow{EF}=\left(\dfrac{1}{3}-x\right)\overrightarrow{BC}}$

 

Ce qui prouve que, quel que soit le nombre $x$, les vecteurs $\overrightarrow{EF}\ $ et $\ \overrightarrow{BC}$ sont colinéaires.

 

3) Déterminons les valeurs de $x$ pour que :

 

$\centerdot\ E\ $ et $\ F$ confondus

 

$\begin{array}{rcl} E\ \text{ et }\ F\ \text{ sont confondus}&\Leftrightarrow&\overrightarrow{EF}=\vec{0}\\\\&\Leftrightarrow&\left(\dfrac{1}{3}-x\right)\overrightarrow{BC}=\vec{0}\quad \text{or, }\ \overrightarrow{BC}\neq\vec{0}\\\\&\Leftrightarrow&\dfrac{1}{3}-x=0\\\\&\Leftrightarrow&x=\dfrac{1}{3}\end{array}$

 

Donc, $E\ $ et $\ F$ sont confondus lorsque $x=\dfrac{1}{3}$

 

$\centerdot\ BCFE$ un parallélogramme

 

$\begin{array}{rcl} BCFE\ \text{ est un parallélogramme}&\Leftrightarrow&\overrightarrow{EF}=\overrightarrow{BC}\\\\&\Leftrightarrow&\left(\dfrac{1}{3}-x\right)\overrightarrow{BC}=\overrightarrow{BC}\\\\&\Leftrightarrow&\left(\dfrac{1}{3}-x\right)\overrightarrow{BC}-\overrightarrow{BC}=\vec{0}\\\\&\Leftrightarrow&\left(\dfrac{1}{3}-x-1\right)\overrightarrow{BC}=\vec{0}\quad \text{or, }\ \overrightarrow{BC}\neq\vec{0}\\\\&\Leftrightarrow&\dfrac{1}{3}-x-1=0\\\\&\Leftrightarrow&x=\dfrac{1}{3}-1\\\\&\Leftrightarrow&x=-\dfrac{2}{3}\end{array}$

 

D'où, $BCFE$ est un parallélogramme lorsque $x=-\dfrac{2}{3}$

Résolvons dans $\mathbb{R}$ les équations et inéquations suivantes :

 

a) $|7-5x|>3$

 

$\begin{array}{rcl}|7-5x|>3&\Leftrightarrow&7-5x>3\  \text{ ou }\  7-5x<-3\\\\&\Leftrightarrow&-5x>3-7\  \text{ ou }\  -5x<-3-7\\\\&\Leftrightarrow&-5x>-4\  \text{ ou }\  -5x<-10\\\\&\Leftrightarrow&x<\dfrac{4}{5}\  \text{ ou }\  x>\dfrac{10}{5}=2\\\\&\Leftrightarrow&x\in\;\left]-\infty\;;\ \dfrac{4}{5}\right[\cup]2\;;\ +\infty[ \end{array}$

 

Ainsi, $\boxed{S=\left]-\infty\;;\ \dfrac{4}{5}\right[\cup\left]2\;;\ +\infty\right[}$

 

b) $|2x-3|\leq\dfrac{5}{2}$

 

$\begin{array}{rcl}|2x-3|\leq\dfrac{5}{2}&\Leftrightarrow&-\dfrac{5}{2}\leq 2x-3\leq\dfrac{5}{2}\\\\&\Leftrightarrow&-\dfrac{5}{2}+3\leq 2x\leq\dfrac{5}{2}+3\\\\&\Leftrightarrow&\dfrac{1}{2}\leq 2x\leq\dfrac{11}{2}\\\\&\Leftrightarrow&\dfrac{1}{2}\times\dfrac{1}{2}\leq x\leq\dfrac{11}{2}\times\dfrac{1}{2}\\\\&\Leftrightarrow&\dfrac{1}{4}\leq x\leq\dfrac{11}{4}\\\\&\Leftrightarrow& x\in\;\left[\dfrac{1}{4}\;;\ \dfrac{11}{4}\right]\end{array}$

 

D'où, $\boxed{S=\left[\dfrac{1}{4}\;;\ \dfrac{11}{4}\right]}$

 

c) $\left|3-\dfrac{x}{2}\right|=\dfrac{x}{3}+6$

 

$\begin{array}{rcl}\left|3-\dfrac{x}{2}\right|=\dfrac{x}{3}+6&\Leftrightarrow&3-\dfrac{x}{2}=\dfrac{x}{3}+6\  \text{ ou }\  3-\dfrac{x}{2}=-\dfrac{x}{3}-6\\\\&\Leftrightarrow&-\dfrac{x}{2}-\dfrac{x}{3}=6-3\  \text{ ou }\  -\dfrac{x}{2}+\dfrac{x}{3}=-6-3\\\\&\Leftrightarrow&-\dfrac{5x}{6}=3\  \text{ ou }\  -\dfrac{x}{6}=-9\\\\&\Leftrightarrow&-5x=18\  \text{ ou }\  -x=-54\\\\&\Leftrightarrow&x=-\dfrac{18}{5}\  \text{ ou }\  x=54\\\\&\Leftrightarrow&x\in\;\left\{-\dfrac{18}{5}\;;\ 54\right\}\end{array}$

 

Ainsi, $\boxed{S=\left\{-\dfrac{18}{5}\;;\ 54\right\}}$

 

d) $|x-3|\leq -2x+1$

 

$-\ $ si $-2x+1<0$ alors, l'inéquation n'admet pas de solutions et donc, $S=\emptyset$

 

On a :

 

$\begin{array}{rcl} -2x+1<0&\Leftrightarrow&-2x<-1\\\\&\Leftrightarrow&x>\dfrac{1}{2}\end{array}$

 

Ainsi, lorsque $x\in\left]\dfrac{1}{2}\;;\ +\infty\right[\;,\ S=\emptyset$

 

$-\ $ si $-2x+1>0$ alors, $x\in\left]-\infty\;;\ \dfrac{1}{2}\right[$

 

On a :

 

$\begin{array}{rcl} |x-3|\leq -2x+1&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x-3&\leq&-2x+1\\\\2x-1&\leq&x-3\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x+2x&\leq&1+3\\\\2x-x&\leq&-3+1\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} 3x&\leq&4\\\\x&\leq&-2\end{array}\right.\\\\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x&\leq&\dfrac{4}{3}\\\\x&\leq&-2\end{array}\right.\end{array}$

 

Donc, $x\in\left]-\infty\;;\ \dfrac{1}{2}\right[\cap\left]-\infty\;;\ \dfrac{4}{3}\right[\cap\left]-\infty\;;\ -2\right[$

 

D'où, $\boxed{S=\left]-\infty\;;\ -2\right[}$

1) a) Vérifions que pour tous réels strictement positifs $a\ $ et $\ x$ tels que : $a>x$, on a l'égalité :

 

$$\dfrac{x}{\sqrt{a+x}-\sqrt{a-x}}=\dfrac{\sqrt{a+x}+\sqrt{a-x}}{2}$$

 

En rendant rationnel le dénominateur du premier membre de cette égalité, on obtient :

 

$\begin{array}{rcl}\dfrac{x}{\sqrt{a+x}-\sqrt{a-x}}&=&\dfrac{x(\sqrt{a+x}+\sqrt{a-x})}{(\sqrt{a+x}-\sqrt{a-x})(\sqrt{a+x}+\sqrt{a-x})}\\\\&=&\dfrac{x(\sqrt{a+x}+\sqrt{a-x})}{(\sqrt{a+x})^{2}-(\sqrt{a-x})^{2}}\\\\&=&\dfrac{x(\sqrt{a+x}+\sqrt{a-x})}{a+x-a+x}\\\\&=&\dfrac{x(\sqrt{a+x}+\sqrt{a-x})}{2x}\\\\&=&\dfrac{\sqrt{a+x}+\sqrt{a-x}}{2}\end{array}$

 

Ainsi, $\boxed{\dfrac{x}{\sqrt{a+x}-\sqrt{a-x}}=\dfrac{\sqrt{a+x}+\sqrt{a-x}}{2}}$

 

b) En déduisons que pour tous réels strictement positifs $a\;,\ m\ $ et $\ p$ tels que : $a>m>p$, on a :

 

$$\dfrac{m}{\sqrt{a+m}-\sqrt{a-m}}<\dfrac{p}{\sqrt{a+p}-\sqrt{a-p}}$$

 

En appliquant les résultats de la question a) à chaque membre de l'inégalité, on obtient :

 

$\dfrac{m}{\sqrt{a+m}-\sqrt{a-m}}=\dfrac{\sqrt{a+m}+\sqrt{a-m}}{2}$

 

$\dfrac{p}{\sqrt{a+p}-\sqrt{a-p}}=\dfrac{\sqrt{a+p}+\sqrt{a-p}}{2}$

 

Donc,

 

$\begin{array}{rcl}\dfrac{m}{\sqrt{a+m}-\sqrt{a-m}}<\dfrac{p}{\sqrt{a+p}-\sqrt{a-p}}&\Leftrightarrow&\dfrac{\sqrt{a+m}+\sqrt{a-m}}{2}<\dfrac{\sqrt{a+p}+\sqrt{a-p}}{2}\\\\&\Leftrightarrow&\left(\dfrac{\sqrt{a+m}+\sqrt{a-m}}{2}\right)^{2}<\left(\dfrac{\sqrt{a+p}+\sqrt{a-p}}{2}\right)^{2}\\\\&\Leftrightarrow&\dfrac{1}{4}\left(\sqrt{a+m}+\sqrt{a-m}\right)^{2}<\dfrac{1}{4}\left(\sqrt{a+p}+\sqrt{a-p}\right)^{2}\\\\&\Leftrightarrow&\left(\sqrt{a+m}+\sqrt{a-m}\right)^{2}<\left(\sqrt{a+p}+\sqrt{a-p}\right)^{2}\end{array}$

 

On a :

 

$\begin{array}{rcl}\left(\sqrt{a+m}+\sqrt{a-m}\right)^{2}&=&(\sqrt{a+m})^{2}+(\sqrt{a-m})^{2}+2\sqrt{a+m}\sqrt{a-m}\\\\&=&a+m+a-m+2\sqrt{(a+m)(a-m)}\\\\&=&2a+2\sqrt{a^{2}-m^{2}}\end{array}$

 

Aussi,

 

$\begin{array}{rcl}\left(\sqrt{a+p}+\sqrt{a-p}\right)^{2}&=&(\sqrt{a+p})^{2}+(\sqrt{a-p})^{2}+2\sqrt{a+p}\sqrt{a-p}\\\\&=&a+p+a-p+2\sqrt{(a+p)(a-p)}\\\\&=&2a+2\sqrt{a^{2}-p^{2}}\end{array}$

 

Ainsi, en faisant la différence de ces deux termes, on obtient :

 

$\begin{array}{rcl}\left(\sqrt{a+m}+\sqrt{a-m}\right)^{2}-\left(\sqrt{a+p}+\sqrt{a-p}\right)^{2}&=&2a+2\sqrt{a^{2}-m^{2}}-2a-2\sqrt{a^{2}-p^{2}}\\\\&=&2(\sqrt{a^{2}-m^{2}}-\sqrt{a^{2}-p^{2}})\end{array}$

 

Par ailleurs, on a :

 

$(\sqrt{a^{2}-m^{2}})^{2}=a^{2}-m^{2}$

 

$(\sqrt{a^{2}-p^{2}})^{2}=a^{2}-p^{2}$

 

Par suite, la différence de ces termes donne :

 

$\begin{array}{rcl}(\sqrt{a^{2}-m^{2}})^{2}-(\sqrt{a^{2}-p^{2}})^{2}&=&a^{2}-m^{2}-a^{2}+p^{2}\\\\&=&-m^{2}+p^{2}\\\\&=&-(m^{2}-p^{2})\\\\&=&-(m-p)(m+p)<0\end{array}$

 

D'où, $\sqrt{a^{2}-m^{2}}-\sqrt{a^{2}-p^{2}}<0$

 

Par conséquent,

 

$$\dfrac{m}{\sqrt{a+m}-\sqrt{a-m}}<\dfrac{p}{\sqrt{a+p}-\sqrt{a-p}}$$

 

2) Simplifions l'expression :

$$\dfrac{1}{(a+b)^{2}}\left(\dfrac{1}{a^{2}}+\dfrac{1}{b^{2}}\right)+\dfrac{2}{(a+b)^{3}}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)$$

Soit :

 

$\begin{array}{rcl}\dfrac{1}{(a+b)^{2}}\left(\dfrac{1}{a^{2}}+\dfrac{1}{b^{2}}\right)+\dfrac{2}{(a+b)^{3}}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)&=&\dfrac{a^{2}+b^{2}}{(a+b)^{2}a^{2}b^{2}}+\dfrac{2(a+b)}{ab(a+b)^{3}}\\\\&=&\dfrac{1}{ab(a+b)^{2}}\left(\dfrac{a^{2}+b^{2}}{ab}+\dfrac{2(a+b)}{(a+b)}\right)\\\\&=&\dfrac{1}{ab(a+b)^{2}}\left(\dfrac{a^{2}+b^{2}}{ab}+2\right)\\\\&=&\dfrac{1}{ab(a+b)^{2}}\left(\dfrac{a^{2}+b^{2}+2ab}{ab}\right)\\\\&=&\dfrac{1}{ab(a+b)^{2}}\left(\dfrac{(a+b)^{2}}{ab}\right)\\\\&=&\dfrac{(a+b)^{2}}{a^{2}b^{2}(a+b)^{2}}\\\\&=&\dfrac{1}{a^{2}b^{2}}\end{array}$

 

D'où, $\boxed{\dfrac{1}{(a+b)^{2}}\left(\dfrac{1}{a^{2}}+\dfrac{1}{b^{2}}\right)+\dfrac{2}{(a+b)^{3}}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)=\dfrac{1}{(ab)^{2}}}$