Corrigé devoir n° 3 maths - 6e

 

On Considère deux points $O\ $ et $\ A$ tels que $OA=5\;cm$ et soit $I$ le milieu du segment $[OA].$

 

Soit $\mathcal{C}_{1}(O\;,\ 2.5)$ le cercle de centre $O$ et de rayon égal à $2.5\;cm$

 

1) Montrons que le point $I$ appartient au cercle $(\mathcal{C}_{1})$

 

Comme $I$ est milieu de $[OA]$ alors, on a :

 

$\begin{array}{rcl} OI&=&\dfrac{OA}{2}\\\\&=&\dfrac{5}{2}\\\\&=&2.5\end{array}$

 

Donc, $OI=2.5\;cm$

 

Alors, on constate que la longueur du segment $[OI]$ est égale au rayon du cercle $(\mathcal{C}_{1}).$

 

De plus, le point $O$, l'une des extrémités de ce segment est le centre du cercle $(\mathcal{C}_{1}).$

 

Par conséquent, le point $I$ appartient au cercle $(\mathcal{C}_{1}).$

 

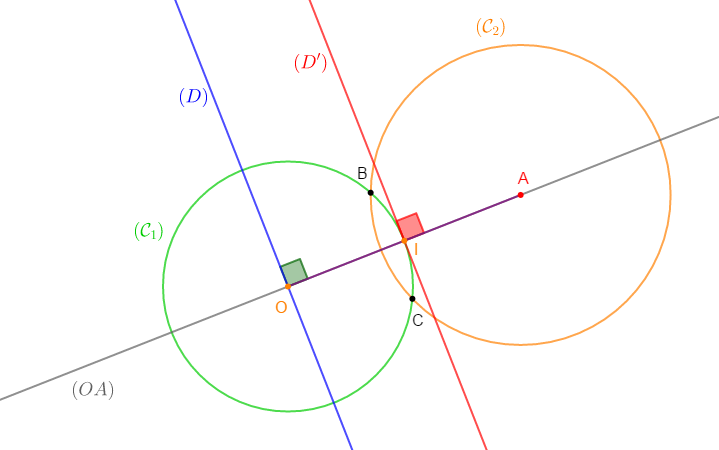
2) Traçons la droite $(D)$ passant par $O$ et perpendiculaire à la droite $(OA)$

 

3) Traçons la droite $(D')$ médiatrice du segment $[OA].$

 

On peut dire que les droites $(D)\ $ et $\ (D')$ sont parallèles.

 

En effet, on a : $(D')$ médiatrice du segment $[OA]$ alors, $(D')$ est perpendiculaire à $(OA).$

 

Ainsi, les droites $(D)\ $ et $\ (D')$ sont perpendiculaires à la même droite $(OA).$

 

Or, deux droites perpendiculaires à une même droite sont parallèles.

 

Donc, les droites $(D)\ $ et $\ (D')$ sont parallèles.

 

4) Traçons $\mathcal{C}_{2}(A\;,\ 3)$, le cercle de centre $A$ et de rayon égal à $3\;cm$

 

5) Donnons la position relative des deux cercles $(\mathcal{C}_{1})\ $ et $\ (\mathcal{C}_{2})$ puis déterminons $(\mathcal{C}_{1})\cap(\mathcal{C}_{2})$

 

On constate que les deux cercles $(\mathcal{C}_{1})\ $ et $\ (\mathcal{C}_{2})$ ont deux points en commun donc, ces deux cercles sont sécants.

 

Soit, $B\ $ et $\ C$ leurs points communs.

 

Alors, on a : $(\mathcal{C}_{1})\cap(\mathcal{C}_{2})=\{B\;;\ C\}$

 

6) Calculons le périmètre et l'aire des cercles $(\mathcal{C}_{1})\ $ et $\ (\mathcal{C}_{2})$

 

On donne : $\pi=3.14$

 

Soit : $\mathcal{P}_{1}$ le périmètre du cercle $(\mathcal{C}_{1})\ $ et $\ \mathcal{P}_{2}$ le périmètre du cercle $(\mathcal{C}_{2})$ alors, on a :

 

$\begin{array}{rcl} \mathcal{P}_{1}&=&2\times r_{1}\times\pi\\\\&=&2\times 2.5\times 3.14\\\\&=&15.7\end{array}$

 

Donc, $\boxed{\mathcal{P}_{1}=15.7\;cm}$

 

$\begin{array}{rcl} \mathcal{P}_{2}&=&2\times r_{2}\times\pi\\\\&=&2\times 3\times 3.14\\\\&=&18.84\end{array}$

 

Ainsi, $\boxed{\mathcal{P}_{2}=18.84\;cm}$

 

Soit : $\mathcal{A}_{1}$ l'aire du cercle $(\mathcal{C}_{1})\ $ et $\ \mathcal{A}_{2}$ l'aire du cercle $(\mathcal{C}_{2})$ alors, on a :

 

$\begin{array}{rcl} \mathcal{A}_{1}&=&r_{1}\times r_{1}\times\pi\\\\&=&2.5\times 2.5\times 3.14\\\\&=&19.625\end{array}$

 

Donc, $\boxed{\mathcal{A}_{1}=19.625\;cm^{2}}$

 

$\begin{array}{rcl} \mathcal{A}_{2}&=&r_{2}\times r_{2}\times\pi\\\\&=&3\times 3\times 3.14\\\\&=&28.26\end{array}$

 

D'où, $\boxed{\mathcal{A}_{2}=28.26\;cm^{2}}$

1) Écrivons en lettres les nombres décimaux suivants :

$$A=6.032\;;\quad B=0.0258\;;\quad C=6.036\;;\quad D=0.0259\;;\quad E=6.03$$

$6.032\;=\;$ Six unités et trente deux millièmes

 

$0.0258\;=\;$ Deux cent cinquante huit dix-millièmes

 

$6.036\;=\;$ Six unités et trente six millièmes

 

$0.0259\;=\;$ Deux cent cinquante neuf dix-millièmes

 

$6.03\;=\;$ Six unités et trois centièmes

 

2) Donnons la correspondance de chacun des chiffres, pour les nombres $A\ $ et $\ B$

 

On a :

 

$A=\underbrace{6}_{\text{unité}}.\underbrace{0}_{\text{dixième }}\underbrace{3}_{\text{ centième }}\underbrace{2}_{\text{ millième}}$

 

$B=\underbrace{0}_{\text{unité}}.\underbrace{0}_{\text{dixième }}\underbrace{2}_{\text{ centième }}\underbrace{5}_{\text{ millième }}\underbrace{8}_{\text{ dix-millième}}$

 

3) Indiquons la partie entière et la partie décimale, pour $C\;,\ D\ $ et $\ E$ 

 

On a :

 

$C=6.036\left\lbrace\begin{array}{rcl} 6&=&\text{partie entière}\\ 0.036&=&\text{partie décimale}\end{array}\right.$

 

$D=0.0259\left\lbrace\begin{array}{rcl} 0&=&\text{partie entière}\\ 0.0259&=&\text{partie décimale} \end{array}\right.$

 

$E=6.03\left\lbrace\begin{array}{rcl} 6&=&\text{partie entière}\\ 0.03&=&\text{partie décimale}\end{array}\right.$

 

4) Rangeons les nombres $A\;,\ B\;,\ C\;,\ D\ $ et $\ E$ dans un ordre décroissant puis dans un ordre croissant.

 

On sait que : $6.036$ est supérieur à $6.032$ qui est supérieur à $6.03$

 

De plus, $6.03$ est supérieur à $0.0259$ qui est supérieur à $0.0258$

 

Ce qui donne alors : $C>A>E>D>B$

 

Ainsi,

 

$-\ $ dans l'ordre croissant, on a :

$$0.0258\;;\ 0.0259\;;\ 6.03\;;\ 6.032\;;\ 6.036$$

$-\ $ dans l'ordre décroissant, on obtient :

$$6.036\;;\ 6.032\;;\ 6.03\;;\ 0.0259\;;\ 0.0258$$

On considère le nombre suivant : $F=101.032$

 

1) Encadrons $F$ par deux entiers naturels consécutifs

 

On a : $101<101.032<102$

 

De plus, $101\ $ et $\ 102$ sont deux entiers naturels consécutifs.

 

Donc, un encadrement de $F$ par deux entiers naturels consécutifs est :

$$101<F<102$$

2) Encadrons $F$ par deux nombres décimaux à un chiffre après la virgule

 

On sait que : $100.9<101.032<101.1$

 

Ainsi, un encadrement de $F$ par deux nombres décimaux à un chiffre après la virgule est donné par :

$$100.9<F<101.1$$

2) Donnons un encadrement du nombre $F$ à $0.01$ près

 

On a : $101.03<101.032<101.04$

 

De plus, $101.04-101.03=0.01$

 

Par suite, un encadrement $F$ à $0.01$ près est donné par :

$$101.03<F<101.04$$