Courbes paramétrées - T S1

On appelle courbe paramétrée $\mathcal{C}$ l'ensemble des points $M(t)$ de coordonnées $x(t)=f(t)$ et $y(t)=g(t)$, $\ t\in\mathbf{I}\subset\mathbb{R}$.

$M(t)$ est appelé le point paramètre $t$

$\overrightarrow{OM}(t)=x(t)\vec{i}+y(t)\vec{j}$

$(\mathcal{C})$ a pour équation paramétrique $\left\lbrace\begin{array}{lcr} x(t) &=& f(t) \\ y(t)= &=& g(t)\end{array}\right.\quad t\in\mathbb{R}$

Cercle, Ellipse, Parabole, Hyperbole

 

$(C)\ \left\lbrace\begin{array}{lcr} x(t) &=& R\sin t \\ y(t) &=& R\cos t\end{array}\right.\quad t\in[0\;,\ 2\pi]$

 

$(\mathcal{E})\ \left\lbrace\begin{array}{lcr} x(t) &=& a\sin t \\ y(t) &=& b\cos t\end{array}\right.\quad t\in[0\;,\ 2\pi]$

 

$(\mathcal{H})\ \left\lbrace\begin{array}{lcr} x(t) &=& \dfrac{a}{\cos t} \\ \\ y(t) &=& b\tan t\end{array}\right.\quad t\in\left]-\dfrac{\pi}{2}\;,\ \dfrac{\pi}{2}\right[\cup\left]\dfrac{\pi}{2}\;,\ \dfrac{3\pi}{2}\right[$

 

$(\mathcal{P})\ \left\lbrace\begin{array}{lcr} x(t) &=& \dfrac{t^{2}}{2p} \\ \\ y(t) &=& t\end{array}\right.\quad t\in\mathbb{R}$

$-\ $ si $t$ décrit $\mathbf{I}$, la position des points $M(t)$ est appelée la trajectoire

$-\ $ le vecteur dérivé $\vec{v}(t)=\dfrac{d(\overrightarrow{OM})}{dt}=x'(t)\vec{i}+y'(t)\vec{j}$

$-\ $ soit $M(t_{0})$ de coordonnées $(x_{0}\;,\ y_{0})$

$\cdot\ $ si $(x'(t)\;,\ y'(t))\neq(0\;,\ 0)$ alors le vecteur $\vec{v}(t_{0})$ est un vecteur directeur de la tangente en $M(t_{0})$

$\cdot\ $ si $(x'(t)\;,\ y'(t))=(0,\ 0)$ alors, $\lim_{t\to t_{0}}\dfrac{y(t)-y(t_{0})}{t-t_{0}}$ détermine la tangente en $M(t_{0})$

Du point de vue cinématique $M(t)$ détermine la position du mobile à l'instant $t$ ; $M(t_{0})$ position initiale.

$\dfrac{d(\overrightarrow{OM})}{dt}$ est le vecteur vitesse.

$\vec{a}(t)=\dfrac{d^{2}(\overrightarrow{OM})}{dt^{2}}=(x''(t)\;,\ y''(t))$ est le vecteur accélération.

Soit la fonction $g : t\longrightarrow ||\vec{v}(t)||$ alors

$-\ $ si $g(t)$ est constante sur $\mathbf{I}$, le mouvement est uniforme

$-\ $ si $g(t)$ est croissante sur $\mathbf{I}$, le mouvement est accéléré

$-\ $ si $g(t)$ est décroissante sur $\mathbf{I}$, le mouvement est retardé

$-\ $ si $\vec{a}(t)\cdot\vec{v}(t)=0$, on dira que le mouvement est uniforme

$-\ $ si $\vec{a}(t)\cdot\vec{v}(t)>0$, on dira que le mouvement est accéléré

$-\ $ si $\vec{a}(t)\cdot\vec{v}(t)<0$, on dira que le mouvement est retardé

Soit la courbe paramétrée $\left\lbrace\begin{array}{lcl}
x(t) &=& f(t)\\
y(t) &=& g(t)
\end{array}
\right.$

Pour étudier une courbe paramétrée on cherche d'abord son ensemble de définition $\mathbf{D}.$

 

Ensuite se ramener à une équation cartésienne si possible.

 

Dans d'autres cas on doit déterminer la parité, la périodicité et les éléments de symétrie pour restreindre le domaine d'étude.

 

Enfin on réalise l'étude dans le domaine restreint

$-\ $ les éléments de symétrie sont :

$\cdot$ si $\left\lbrace\begin{array}{lcl}
x(-t) &=& x(t)\\
y(-t) &=& y(t)
\end{array}
\right.$ alors $M(-t)=M(t)$ $\Longrightarrow \: \mathcal{C}_{]-\infty;\ 0]\bigcap\mathbf{D}}=\mathcal{C}_{[0;\ +\infty[\bigcap\mathbf{D}}$

$M(-t)\ $ et $\ M(t)$ sont symétriques par rapport à la droite d'équation : $y=x$

$\cdot\ $ si $\left\lbrace\begin{array}{lcl}
x(-t) &=& -x(t)\\
y(-t) &=& y(t)
\end{array}
\right.$ alors, $M(-t)\ $ et $\ M(t)$ sont symétriques par rapport à $(y'Oy)$.

$\mathcal{C}_{]-\infty;\ 0]\bigcap\mathbf{D}}$ est l'image de $\mathcal{C}_{[0;\ +\infty[\bigcap\mathbf{D}}$ par la symétrie axiale d'axe $(y'Oy)$

$\cdot\ $ si $\left\lbrace\begin{array}{lcl}
x(-t) &=& x(t)\\
y(-t) &=& -y(t)
\end{array}
\right.$ alors, $M(-t)$ et $M(t)$ sont symétriques par rapport à $(x'Ox)$.

$\mathcal{C}_{]-\infty;\ 0]\bigcap\mathbf{D}}$ est l'image de $\mathcal{C}_{[0;\ +\infty[\bigcap\mathbf{D}}$ par la symétrie axiale d'axe $(x'Ox)$

$\cdot\ $ si $\left\lbrace\begin{array}{lcl}
x(-t) &=& -x(t)\\
y(-t) &=& -y(t)
\end{array}
\right.$ alors, $M(-t)\ $ et $\ M(t)$ sont symétriques par rapport à $O$.

$\mathcal{C}_{]-\infty;\ 0]\bigcap\mathbf{D}}$ est l'image de $\mathcal{C}_{[0;\ +\infty[\bigcap\mathbf{D}}$ par la symétrie centrale de centre $O$

$\cdot$ soit $t+T\in\mathbf{D}$,  si $\left\lbrace\begin{array}{lcl}
x(t+T) &=& x(t)\\
y(t+T) &=& y(t)
\end{array}
\right.$ alors, $M(t+T)=M(t)$.

On étudie $\mathcal{C}$ sur $\mathbf{D}\bigcap[0,\ T]$ ; $\ \left[-\frac{T}{2};\ \frac{T}{2}\right]\bigcap\mathbf{D}$

Si en plus $M(-t)$ est symétrique à $M(t)$ par rapport à un axe ou à $O$, on prendra $\mathbf{D}_{E}=\left[0;\ \frac{T}{2}\right]\bigcap\mathbf{D}$

Soit à étudier la courbe paramétrée suivante :

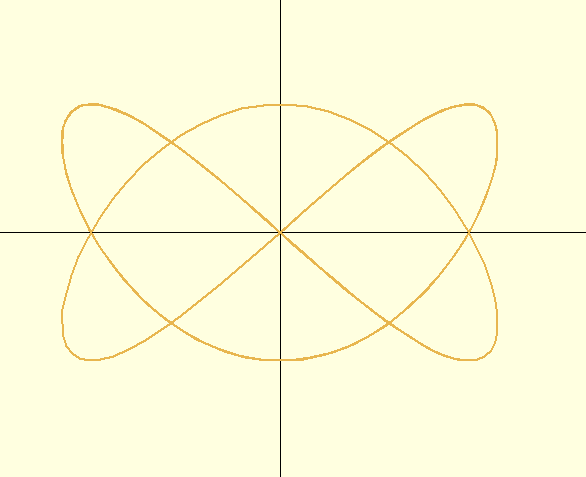
$$\left\lbrace\begin{array}{lcl} x(t) &=& \sin 2t\\ y(t) &=& \sin 3t \end{array}\right.\quad t\in\mathbb{R}$$

Comme $x(t)$ est périodique de période $\pi$ et $y(t)$ périodique de période $\dfrac{2\pi}{3}$ alors, pour la courbe paramétrée, on obtient une période $T=2\pi.$

 

Donc l'étude peut se faire sur un intervalle $\mathbf{I}$ de longueur $2\pi.$

 

Aussi, on a : $\left\lbrace\begin{array}{lcl} x(-t) &=& \sin -2t\\ y(-t) &=& \sin -3t \end{array}\right.\;\Rightarrow\;\left\lbrace\begin{array}{lcl} x(-t) &=& -\sin 2t\;=\;-x(t)\\ y(-t) &=& -\sin 3\;t=\;-y(t) \end{array}\right.$

 

donc $M(t)\ $ et $\ M(-t)$ sont symétrique par rapport à $O$ , origine du repère.

 

Ainsi, on peut restreindre le domaine d'étude $\mathbf{D}_{E}.$ 

 

Soit $\mathbf{D}_{E}=[0\;,\ \pi]$

 

On a : $$\left\lbrace\begin{array}{lcl} x'(t) &=& 2\cos 2t\\ y'(t) &=& 3\cos 3t \end{array}\right.$$

$\begin{array}{rcl} x'(t)\geq 0 &\Leftrightarrow & \cos 2t\geq 0 \\ \\ &\Leftrightarrow & 2t\in\left[-\dfrac{\pi}{2}\;,\ \dfrac{\pi}{2}\right]\;[2\pi] \\ \\ &\Leftrightarrow & k\pi-\dfrac{\pi}{4}\leq t\leq\dfrac{\pi}{4}+k\pi \end{array}$

 

$\begin{array}{rcl} y'(t)\geq 0 &\Leftrightarrow & \cos 3t\geq 0 \\ \\ &\Leftrightarrow & 3t\in\left[-\dfrac{\pi}{2}\;,\ \dfrac{\pi}{2}\right]\;[2\pi] \\ \\ &\Leftrightarrow & \dfrac{2k\pi}{3}-\dfrac{\pi}{6}\leq t\leq\dfrac{\pi}{6}+\dfrac{2k\pi}{3} \end{array}$

 

$$\begin{array}{|c|lclclclclclcr|} \hline t  & 0 &  & \pi/6 &  & \pi/4 & & \pi/2 &  & 3\pi/4 &  & 5\pi/6 &  & \pi \\ \hline x'(t) &  & + &  & + & 0 & - &  & - & 0 & +  &  & + & \\ \hline &  &  &  &  & 1 &  &  &  &  &  &  &  & 0   \\ &  &  &  &\nearrow &  &\searrow &  & & & & & \nearrow & \\ x(t) &  &  & \sqrt{2}/2 &  &  &  & 0 &  &  &  & -\sqrt{3}/2 &  &  \\ &  & \nearrow &  &  &  &  &  &\searrow &  & \nearrow &  &  &  \\ & 0 &  &  &  &  &  &  &  & -1 &  &  &  &   \\ \hline &  &  & 1 &  &  &  &  &  &  &  & 1 &  &   \\ &  &  &  & \searrow &  &  &  &  &  & \nearrow &  &  &   \\ y(t) &  & \nearrow &  &  & \sqrt{3}/2 &  &  &  & \sqrt{2}/2 &  &  & \searrow &   \\ &  &  &  &  &  & \searrow &  & \nearrow &  &  &  &  &   \\ & 0 &  &  &  &  &  & -1 &  &  &  &  &  & 0  \\ \hline y'(t) &  & + & 0 & - &  & - & 0 & + &  & +  & 0 & - & \\ \hline\end{array}$$