Dénombrement - T S

Le cardinal d'un ensemble $E$ est le nombre d'éléments de l'ensemble $E$ et on note : $Card\;E$

 

Exemple :

 

$E=\{a\;,\ b\;,\ c\;,\ x\;,\ y\;,\ z\;,\ t\}\;;\quad Card\;E=7$

 

Remarque :

 

Le cardinal de l'ensemble vide $\emptyset$ est égal à 0. On note $Card\;\emptyset=0$

Soit $A$ et $B$ deux ensembles finis on a :

 

$\centerdot\ \ A\cup B=\{x\;;\;x\in A\;\text{ ou }\;x\in B\}$

 

$\centerdot\ \ A\cap B=\{x\;;\;x\in A\;\text{ et }\;x\in B\}$

 

$\centerdot\ \ A\setminus B=\{x\;;\;x\in A\;\text{ et }\;x\notin B\}$

 

$\centerdot\ \ B\setminus A=\{x\;;\;x\in B\;\text{ et }\;x\notin A\}$

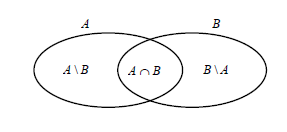
$-\ A$ et $B$ sont dits disjoints si $$A\cap B=\emptyset$$

 

$-\ $ Si deux ensembles $E$ et $F$ sont disjoints, alors $$Card\;E\cup F=Card\;E+Card\;F$$

 

On a $Card\;A\cup B=Card(A\cup(B\setminus A))=Card\;A+Card(B\setminus A)$

 

Or, $B=(B\setminus A)\cup(A\cap B)$

 

Donc, $Card\;B=Card(B\setminus A)+Card\;A\cap B$

 

Ainsi, $Card(B\setminus A)=Card\;B-Card\;A\cap B$

 

D'où, $$\boxed{Card\;A\cup B=Card\;A+Card\;B-Card\;A\cap B}$$

 

$\centerdot\ \ $ Soit $\Omega$ un ensemble et $E$ une partie non vide de $\Omega\;;\ E\subset\Omega.$ 

 

Le complémentaire de $E$ dans $\Omega$ est l'ensemble des éléments de $\Omega$ n'appartenant pas à $E$ noté $\overline{E}=\{x\in\Omega\;;\ x\notin E\}.$

 

On dira que deux ensembles $A$ et $B$ sont complémentaires dans $\Omega$ si $$\left\lbrace\begin{array}{rcl} A\cap B &=& \emptyset \\ A\cup B &=& \Omega\end{array}\right.$$

 

$\centerdot\ \ $ Soit $\Omega$ un ensemble, on dira que, $n$ parties non vides de $\Omega\;;\ $ $A_{1}\;,\ A_{2}\;,\ \ldots\;,\ A_{n}\;,$ forment une partition de $\Omega$ si

$$\left\lbrace\begin{array}{rcr} A_{i}\cap A_{j} &=& \emptyset\quad\text{ si }\;i\neq j \\ \\ A_{1}\cup A_{2}\cup\ldots\cup A_{n} &=& \bigcup_{i=1}^{n} A_{i}\;=\;\Omega\end{array}\right.$$

Dans une classe de 35 élèves, 20 élèves pratiquent le Basket-ball, 15 élèves pratiquent le Foot-ball. Sachant qu'il y a 2 élèves qui ne pratiquent aucun de ces deux sports, déterminer :

 

1) le nombre d'élèves qui pratiquent le Basket et le Foot à la fois 

 

2) le nombre d'élèves qui pratiquent exactement 1 sport.

Soit $E$ l'ensemble des élèves de la classe, $F$ l'ensemble des élèves qui pratiquent le Foot et $B$ l'ensemble des élèves qui pratiquent le Basket.

 

Alors, $E\setminus(F\cup B)$ constitue l'ensemble des élèves qui ne pratiquent aucun sport.

 

Donc, $Card\;E=35\;,\ Card(E\setminus(F\cup B))=2\;,\ Card\;F=15$ et $Card\;B=20$

 

1) On a :

 

$\begin{array}{rcl} Card(E\setminus(F\cup B)) &=& Card\;E-Card(F\cup B)=2 \\ \\ &=& Card\;E-Card\;F-Card\;B+Card\;F\cap B=2 \\ \\ &=& 35-15-20+Card\;F\cap B=2 \\ \\ \Rightarrow\;Card\;F\cap B &=& 2 \end{array}$

 

il y a donc 2 élèves qui pratiquent à la fois le Basket et le Foot.

 

2) On a :

 

$\begin{array}{rcl} Card((F\setminus B)\cup(B\setminus F)) &=& Card\;F-Card\;F\cap B+Card\;B-Card\;F\cap B \\ \\ &=& Card\;F+Card\;B-2\;Card\;F\cap B \\ \\ &=& 15+20-4 \\ \\ &=& 31 \end{array}$

 

Donc, 31 élèves pratiquent exactement 1 sport.

Le produit cartésien de deux ensembles $A$ et $B$ est l'ensemble des couples d'éléments $(a\;,\ b)$ tels que $a\in A$ et $b\in B.$

 

On note $A\times B=\{(a\;,\ b)\;;\;a\in A\;\text{ et }\;b\in B\}$

 

Soient $A=\{a_{1}\;,\ a_{2}\;,\ \ldots\;,\ a_{n}\}\;;\ Card\;A=n$ et $B=\{b_{1}\;,\ b_{2}\;,\ \ldots\;,\ b_{p}\}\;;\ Card\;B=p$ deux ensembles finis.

 

Notons $E_{i}=\{(a_{i}\;,\ b_{j})\;;\ 1\leq j\leq p\}$

 

Alors, $E_{1}=\{(a_{1}\;,\ b_{1})\;,\ (a_{2}\;,\ b_{2})\;,\ \ldots\;,\ (a_{1}\;,\ b_{p})\}\;;\ Card\;E_{1}=p$

 

Ainsi, $Card\;E_{i}=p\;;\ \forall\;i$

 

Le produit cartésien de $A$ et $B$ est donc donné par $$A\times B=\bigcup_{i=1}^{n}E_{i}$$

Donc,

 

$\begin{array}{rcl} Card(A\times B) &=& \sum_{i=1}^{n} Card\;E_{i}\\ \\ &=& \sum_{i=1}^{n}p \\ \\ &=& n\times p \\ \\ &=& Card\;A\times Card\;B \end{array}$

 

Par suite, si $A_{1}\;,\ A_{2}\;,\ \ldots\;,\ A_{n}$ sont $n$ ensembles de cardinal fini, alors : $$Card(A_{1}\times A_{2}\times\ldots\times A_{n})=Card\left(\times_{i=1}^{n}A_{i}\right)=\prod_{i=1}^{n}Card\;A_{i}$$

 

D'où : $$\boxed{Card(A_{1}\times A_{2}\times\ldots\times A_{n})=\prod_{i=1}^{n}Card\;A_{i}}$$

Un élève se présente à l'examen oral avec 12 leçons d'histoire étudiées dont 9 sont sues, 10 leçons de géographie étudiées dont 7 sont sues. Il doit tirer une leçon d'histoire et une leçon de géographie et traiter les deux sujets à la fois.

 

1) Déterminer le nombre de choix possibles.

 

2) Déterminer le nombre de choix dans chacun des cas suivants :

 

$A=$ "l'élève sait traiter les deux sujets"

 

$B=$ "l'élève sait traiter exactement 1 sujet"

 

$C=$ "l'élève ne sait traiter aucun sujet"

 

$D=$ "l'élève sait traiter au moins 1 sujet"

 

$E=$ "l'élève sait traiter au plus 1 sujet" 

Soit $H$ l'ensemble des leçons d'histoire ;  $Card\;H=12$

 

$G$ l'ensemble des leçons de géographie ; $Card\;G=10$

 

L'ensemble de toutes les possibilités appelé univers est $\Omega=H\times G=\{(h\;,\ g)\;;\ h\in H\;,\ g\in G\}$

 

1)

 

$\begin{array}{rcl} Card\;\Omega &=& Card(H\times G) \\\\ &=& Card\;H\times Card\;G \\\\ &=& 12\times 10 \\\\ &=& 120 \end{array}$

 

Donc on dispose de $120$ possibilités.

 

2) Soit $H_{s}$ l'ensemble des leçons d'histoire sues ; $Card\;H_{s}=9\ $ et $\ Card\;\overline{H}_{s}=3$

 

$G_{s}$ l'ensemble des leçons de géographie sues ; $Card\;G_{s}=7\ $ et $\ Card\;\overline{G}_{s}=3$

 

$\centerdot\ \ A=$ "l'élève sait traiter les deux sujets"

 

On a : $A=H_{s}\times G_{s}$

 

Donc,

 

$\begin{array}{rcl} Card\;A &=& Card(H_{s}\times G_{s}) \\\\ &=& Card\;H_{s}\times Card\;G_{s} \\\\ &=& 7\times 9 \\\\ &=& 63 \end{array}$

 

D'où, $Card\;A=63$

 

$\centerdot\ \ B=$ "l'élève sait traiter exactement 1 sujet"

 

Soit $B=(H_{s}\times \overline{G}_{s})\cup(\overline{H}_{s}\times G_{s})$ avec $(H_{s}\times \overline{G}_{s})\cap(\overline{H}_{s}\times G_{s})=\emptyset$

 

Donc,

 

$\begin{array}{rcl} Card\;B &=& Card((H_{s}\times \overline{G}_{s})\cup(\overline{H}_{s}\times G_{s})) \\\\ &=&  Card(H_{s}\times \overline{G}_{s})+Card(\overline{H}_{s}\times G_{s}) \\\\ &=& Card\;H_{s}\times Card\;\overline{G}_{s}+Card\;\overline{H}_{s}\times Card\;G_{s} \\\\ &=& 9\times 3+3\times 7 \\\\ &=& 27+21=48 \end{array}$

 

D'où, $Card\;B=48$

 

$\centerdot\ \ C=$ "l'élève ne sait traiter aucun sujet"

 

On a : $C=(\overline{H}_{s}\times \overline{G}_{s})$

 

Donc,

 

$\begin{array}{rcl} Card\;C &=& Card(\overline{H}_{s}\times \overline{G}_{s}) \\\\ &=& Card\;\overline{H}_{s}\times Card\;\overline{G}_{s} \\\\ &=& 3\times 3=9\end{array}$

 

D'où, $Card\;C=9$

 

Remarque : $C\ $ et $\ D$ sont contraires.

 

$\centerdot\ \ D=$ "l'élève sait traiter au moins 1 sujet"

 

Alors,

 

$\begin{array}{rcl} Card\;D &=& Card\;A+Card\;B \\\\ &=& 63+48=111\end{array}$

 

D'où, $Card\;D=111$

 

$\centerdot\ \ $ E = "l'élève sait traiter au plus 1 sujet"

 

Alors,

 

$\begin{array}{rcl} Card\;E &=& Card\;B+Card\;C \\\\ &=& 48+9=57 \end{array}$

 

D'où, $Card\;E=57$

Soient $n\in\mathbb{N}^{*}\ $ et $\ E$ un ensemble fini à $n$ éléments. $E=\{e_{1}\;,\ e_{2}\;,\ \ldots\;,\ e_{n}\}\;;\ Card\;E=n$

 

Une p-listes de $E$ est une suite ordonnée de $p$ éléments appartenant à $E.$

 

Exemple :

 

une 2-listes = couples $(e_{1}\;,\ e_{2})\;;\ (e_{2}\;,\ e_{7})\;;\ (e_{3}\;,\ e_{4})\;;\ \ldots$

 

une 3-listes = triplets $(e_{1}\;,\ e_{1}\;,\ e_{2})\;;\ (e_{2}\;,\ e_{3}\;,\ e_{7})\;;\ (e_{2}\;,\ e_{2}\;,\ e_{2})\;;\ \ldots$

 

une 4-listes = quadruplets

 

$\vdots$

 

une p-listes = p-uplets (des groupes de $p$ éléments)

Soit $E$ un ensemble fini tel que $Card\;E=n$, alors

 

le nombre de 2-listes = $n\times n=n^{2}$

 

le nombre de 3-listes = $n\times n\times n=n^{3}$

 

$\vdots$

 

le nombre de p-listes = $\underbrace{n\times n \ldots\times n}_{p\ \mathrm{fois}}=n^{p}$

 

Donc, le nombre de p-listes d'un ensemble à $n$ éléments est égal à $n^{p}.$

Soit $E$ un ensemble fini de cardinal $n.$ Un arrangement à $p$ éléments de $E$ est une p-listes de $E$ où les éléments sont deux à deux distincts.

 

Exemple : arrangement de 2 éléments $(e_{1}\;,\ e_{3})\;;\ (e_{i}\;,\ e_{j})_{i\neq j}$

 

Le nombre d'arrangements à $p$ éléments dans un ensemble à $n$ éléments est égal à $$n(n-1)(n-2)\times\ldots\times(n-p+1)=A_{n}^{p}$$

$$A_{n}^{p}=\dfrac{n!}{(n-p)!}=n\times(n-1)\times(n-2)\times\ldots\ldots\times(n-p+1)$$

Soit $E$ un ensemble fini à $n$ éléments. Une permutation de $E$ est un arrangement à $n$ éléments dans un ensemble à $n$ éléments.

 

Le nombre de permutations d'un ensemble à $n$ éléments est égal à $n!=A_{n}^{n}.$

 

Remarque : $0!=1$

Une urne contient $6$ boules rouges numérotées de $1$ à $6\;;\ 5$ noires numérotées de $1$ à $5\;;\ 2$ vertes numérotées $1$ et $2\;;\ 3$ jaunes numérotées $1\;;\ 2\ $ et $\ 3.$

 

1) On tire successivement trois $(3)$ boules de l'urne en remettant les boules tirées dans l'urne après chaque tirage.

 

a) Déterminer le nombre de tirages possibles.

 

b) Déterminer le nombre de tirages possibles dans chacun des cas suivants :

 

i) les $3$ boules tirées sont de même couleur

 

ii) les $3$ boules tirées portent le même numéro

 

iii) les $3$ boules tirées sont de couleurs différentes

 

iv) on a tiré exactement une boule noire

 

v) on a tiré au moins $2$ boules rouges

 

2) On tire successivement trois $(3)$ boules de l'urne sans remettre les boules tirées dans l'urne.

 

a) Déterminer le nombre de tirages possibles.

 

b) Déterminer le nombre de tirages possibles dans chacun des cas suivants :

 

i) les $3$ boules tirées sont de même couleur

 

ii) les $3$ boules tirées portent le même numéro

Soit $Card\;U$ le nombre total de boules dans l'urne.

 

On a : $Card\;U=16$

 

L'ensemble des possibilités appelé univers $\Omega$, est l'ensemble des $3-$listes pris dans un ensemble à $16$ éléments.

 

1) tirage avec remise

 

a) on a $Card\;\Omega=16^{3}=4\,096$

 

b) nombre de tirages possibles dans les cas suivants :

 

i) soit $A=$"les $3$ boules tirées sont de même couleur" ; soit $3R\ $ ou $\ 3N\ $ ou $\ 3V\ $ ou $\ 3J$

 

Donc on a : $Card\;A=6^{3}+2^{3}+5^{3}+3^{3}=376$

 

ii) $B=$"les $3$ boules tirées portent le même numéro" ; soit $3(1)\ $ ou $\ 3(2)\ $ ou $\ 3(3)\ $ ou $\ 3(4)\ $ ou $\ 3(5)\ $ ou $\ 3(6)$

 

Donc, $Card\;B=4^{3}+4^{3}+3^{3}+2^{3}+2^{3}+1^{3}=172$

 

iii) $C=$"les 3 boules tirées sont de couleurs différentes" ; soit $RNV\ $ ou $\ RNJ\ $ ou $\ NJV\ $ ou $\ RVJ$

 

Ainsi, $Card\;C=(6\times 5\times 2)\times 6+(6\times 5\times 3)\times 6+(5\times 2\times 3)\times 6+(6\times 2\times 3)\times 6=1\,296$

 

iv) $D=$"on a tiré exactement une boule noire" ; soit $1N\ $ et $\ 2(VJR)$

 

On a : $Card\;D=5\times 11^{2}\times 3=1\,815$

 

v) $E=$"on a tiré au moins 2 boules rouges" ; soit $2R\ $ et $\ 1(NVJ)\ $ ou $\ 3R$

 

Donc on a : $Card\;E=(6^{2}\times 10)\times 3+6^{3}=1\,296$

 

2) cas d'un tirage sans remise

 

a) alors on a $Card\;\Omega=A_{16}^{3}=3\,360$

 

b) nombre de tirages possibles dans les cas suivants :

 

i) soit $A=$"les $3$ boules tirées sont de même couleur" ; soit $3R\ $ ou $\ 3N\ $ ou $\ 3J$

 

Ainsi, $Card\;A=A_{6}^{3}+A_{5}^{3}+A_{3}^{3}=186$

 

ii) $B=$"les $3$ boules tirées portent le même numéro" ; soit $3(1)\ $ ou $\ 3(2)\ $ ou $\ 3(3)$

 

Donc, $Card\;B=A_{4}^{3}+A_{4}^{3}+A_{3}^{3}=54$

Soit $E$ un ensemble tel que $Card\;E=n\;;\ n\in\mathbb{N}$

 

Une partie ou combinaison à $p$ éléments dans un ensemble à $n$ éléments est un sous-ensemble de $E$ à $p$ éléments $(p\leq n).$

Le nombre de parties ou combinaisons à $p$ éléments dans un ensemble à $n$ éléments est égal à $$\dfrac{A_{n}^{p}}{p!}=C_{n}^{p}=\dfrac{n!}{p!(n-p)!}$$

 

Exemple :

 

une urne contient 10 boules numérotées de 0 à 9. On en tire simultanément trois (3). Combien de tirages différents peut-on obtenir ?

 

L'ensemble des possibilités appelé univers $\Omega$, est l'ensemble des combinaisons à 3 éléments dans un ensemble à 10 éléments.

$\centerdot\ \ C_{n}^{n}=1$

 

$\centerdot\ \ C_{n}^{n-1}=n$

 

$\centerdot\ \ C_{n}^{p}=C_{n}^{n-p}$

 

$\centerdot\ \ C_{n}^{1}=n$

 

On a : $C_{n}^{p}=\dfrac{n!}{p!(n-p)!}$

 

Donc,

 

$\begin{array}{rcl} C_{n}^{n-p} &=& \dfrac{n!}{p!(n-p)!} \\ \\ &=& \dfrac{n!}{(n-p)!(n-(n-p))!} \\ \\ &=& \dfrac{n!}{(n-p)!p!} \\ \\ &=& C_{n}^{p} \end{array}$

 

$\centerdot\ \ C_{n}^{p}+C_{n}^{p-1}=C_{n+1}^{p}$

 

On a :

 

$\begin{array}{rcl} C_{n}^{p}+C_{n}^{p-1} &=& \dfrac{n!}{p!(n-p)!}+\dfrac{n!}{p!(n-p)!} \\ \\ &=& n!\left[\dfrac{n+1-p+p}{p!(n+1-p)!}\right] \\ \\ &=& n!\times\dfrac{(n+1)}{p!(n+1-p)!} \\ \\ &=& \dfrac{n!\times(n+1)}{p!(n+1-p)!} \\ \\ &=& \dfrac{(n+1)!}{p!(n+1-p)!} \\ \\ &=& C_{n+1}^{p}  \end{array}$

 

$\centerdot\ \ $ Formule du binôme de Newton

 

Pour tous nombres complexes $a$ et $b$ et tout entier naturel $n$ non nul on a :

 

$$(a+b)^{n}=\sum_{k=0}^{n}C_{n}^{k}a^{k}b^{n-k}$$

 

Exemple :

 

$\begin{array}{rcl} (a+b)^{2} &=& \sum_{k=0}^{2}C_{2}^{k}a^{k}b^{2-k} \\ \\ &=& C_{2}^{0}a^{0}b^{2}+C_{2}^{1}a^{1}b^{1}+C_{2}^{2}a^{2}b^{0} \\ \\ &=& b^{2}+2ab+a^{2}  \end{array}$

 

$\begin{array}{rcl} (a+b)^{3} &=& \sum_{k=0}^{3}C_{3}^{k}a^{k}b^{3-k} \\ \\ &=& C_{3}^{0}a^{0}b^{3}+C_{3}^{1}a^{1}b^{2}+C_{3}^{2}a^{2}b^{1}+C_{3}^{3}a^{3}b^{0} \\ \\ &=& b^{3}+3ab^{2}+3a^{2}b+a^{3}  \end{array}$

 

$\centerdot\ \ $ Triangle de Pascal

 

La relation de Pascal permet de calculer les coefficient binomiaux de la façon suivante : pour trouver un certain coefficient, on additionne dans le tableau suivant les coefficients situés "juste au dessus" et "juste au dessus à gauche" entre eux :

 

$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|} \hline n\backslash p & 0 & 1 & 2 & 3 & 4 & \ldots & p-1 & p &\ldots & n-1 & n \\ \hline 0 & 1 &  &  &  &  &  &  &  & &  &  \\ \hline 1 & 1 & 1 &  &  &  &  &  &  & &  &  \\ \hline 2 & 1 & 2 & 1 &  &  &  &  &  & &  &  \\ \hline 3 & 1 & 3 & 3 & 1 &  &  &  &  & &  &  \\ \hline 4 & 1 & 4 & 6 & 4 & 1 &  &  &  & &  &  \\ \hline\ldots & \ldots & \ldots & \ldots & \ldots & \ldots & \ldots & \ldots & \ldots & \ldots & \ldots & \ldots \\ \hline n-1 & 1 & n-1 &  &  &  & \ldots & \boxed{C_{n-1}^{p-1}} &  \boxed{C_{n-1}^{p}} & \ldots & 1 &  \\ \hline n & 1 & n &  &  &  & \ldots & \boxed{C_{n}^{p-1}} &  \boxed{C_{n}^{p}} & \ldots & n & 1 \\ \hline\end{array}$$

 

Ainsi, pour $0\leq p\leq 10$ et $0\leq n\leq 10$ on obtient le tableau des coefficients suivant :

 

$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|} \hline n\backslash p & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ \hline 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \hline 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \hline 2 & 1 & 2 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \hline 3 & 1 & 3 & 3 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \hline 4 & 1 & 4 & 6 & 4 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ \hline 5 & 1 & 5 & 10 & 10 & 5 & 1 & 0 & 0 & 0 & 0 & 0 \\ \hline 6 & 1 & 6 & 15 & 20 & 15 & 6 & 1 & 0 & 0 & 0 & 0 \\ \hline 7 & 1 & 7 & 21 & 35 & 35 & 21 & 7 & 1 & 0 & 0 & 0 \\ \hline 8 & 1 & 8 & 28 & 56 & 70 & 56 & 28 & 8 & 1 & 0 & 0 \\ \hline 9 & 1 & 9 & 36 & 84 & 126 & 126 & 84 & 36 & 9 & 1 & 0 \\ \hline 10 & 1 & 10 & 45 & 120 & 210 & 252 & 210 & 120 & 45 & 10 & 1 \\ \hline\end{array}$$