Devoir n° 2 - TL

Classe: 
Terminale
 

Exercice 1

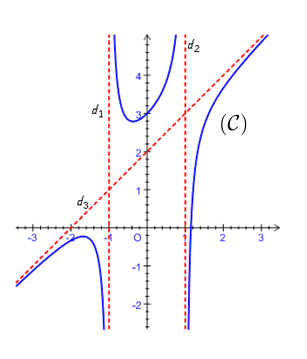
On donne ci-dessous la courbe $(\mathcal{C})$ représentative d'une fonction $f$ et les droites $d_{1}\;,\ d_{2}\ $ et $\ d_{3}$ d'équations respectives :
 
$d_{1}\ :\ x=-1$
 
$d_{2}\ :\ x=1$
 
$d_{3}\ :\ y=x+2$
 
1) En utilisant le graphique, traduire en termes de limites chacune des donnés suivantes :
 
$d_{1}$ est asymptote à $(\mathcal{C})$
 
$d_{2}$ est asymptote à $(\mathcal{C})$
 
$d_{3}$ est asymptote à $(\mathcal{C})$
 
2) Donner, en utilisant le graphique le signe de $f(x)-(x+2)$

 

 
 

Exercice 2

La fonction $f$ a pour tableau de variation :
$$\begin{array}{|r|lcrclcccr|}\hline x&-\infty&&&-1&&&0&&+\infty\\ \hline&&&+\infty&||&+\infty&&&&7\\ f&&\nearrow&&||&&\searrow&&\nearrow&\\&-\infty&&&||&&&3&&\\ \hline\end{array}$$
 
1) Donner dans chacun des cas le nombre de solutions de l'équation (pour cette question et uniquement celle-ci, aucune justification n'est demandée)
$$f(x)=10\;;\ f(x)=5\;;\ f(x)=0\;;\ f(x)=-1$$
2) Comparer si c'est possible $f\left(-\dfrac{1}{2}\right)\ $ et $\ f(0)\;;\quad f(2)\ $ et $\ f(3)$
 
3) Déterminer :
$$\lim_{\substack{x \to 0 \\ x>0}}f\left(\dfrac{1}{x}\right)\;;\ \lim_{x\rightarrow +\infty}f\left(\dfrac{1}{x}\right)\;;\ \lim_{x\rightarrow -\infty}f\left(\dfrac{x+1}{3-x}\right)\;;\ \lim_{x\rightarrow +\infty}f(1-x^{2})$$
 

Exercice 3

On considère la fonction $f$ définie par :
$$f(x)=\dfrac{-2x^{2}+3x-9}{1-x}$$
On note $(\mathcal{C})$ la courbe représentative de $f$ dans le plan rapporté à un repère orthogonal. On prendra comme unités graphiques $1\;cm$ sur l'axe des abscisses et $0.5\;cm$ sur l'axe des ordonnées.
 
1) Déterminer l'ensemble de définition $D$ de la fonction $f.$
 
2) Montrer que pour tout réel $x$ de $D$, on a :
$$f(x)=2x-1-\dfrac{8}{1-x}$$
3) Déterminer les limites de $f$ aux bornes de $D.$
 
4) Montrer que $(\mathcal{C})$ a une asymptote verticale $\mathfrak{D}_{1}$ et une asymptote oblique $\mathfrak{D}_{2}$ dont on donnera les équations. Étudier la position de $(\mathcal{C})$ par rapport à $\mathfrak{D}_{2}.$
 
5) Calculer la dérivée de $f$ et étudier son signe.
 
6) Dresser le tableau des variations de $f.$
 
7) Reproduire et compléter le tableau de valeurs suivants. (les valeurs de $f(x)$ seront données à $10^{-1}$ près)
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|}\hline x&-10&-8&-6&-4&-2&0&2&4&6&8&10\\ \hline f(x)&&&&&&&&&&&\\ \hline \end{array}$$
8) Justifier que l'équation $f(x)=10$ a, sur l'intervalle $]3\;;\ +\infty[$, une solution unique $\alpha$ dont on donnera une valeur approchée à $10^{-2}$ près.
 
9) Tracer la courbe $(\mathcal{C})$ et ses deux asymptotes $\mathfrak{D}_{1}\ $ et $\ \mathfrak{D}_{2}.$
 
10) Déterminer l'équation de la tangente $T$ à la courbe $(\mathcal{C})$ au point d'abscisse $2.$ Tracer $T$ sur le dessin précédent.
 
Quelles sont les coordonnées du point d'intersection de $T$ avec l'axe des abscisse ?
 
11) Résoudre l'équation $f(x)=10$ et vérifier la valeur approchée de $\alpha$ trouvée au 8)
 
12) Résoudre l'inéquation $f(x)\leq 10$ et vérifier graphiquement le résultat obtenu.
 
 
 
$$\text{Durée 3 heures}$$
Auteur: 
Abdoulaye Diagne

Commentaires

Anonyme (non vérifié)

lun, 01/18/2021 - 13:36

Pdf

EDGARD MARTIAL ... (non vérifié)

mer, 11/10/2021 - 06:54

Important site pour améliorer ces capacités,, s'entraîner surtout. Merci pour votre soutien

EDGARD MARTIAL ... (non vérifié)

mer, 11/10/2021 - 06:55

Important site pour améliorer ces capacités,, s'entraîner surtout. Merci pour votre soutien

Ajouter un commentaire