Devoir n° 28 1e S2
Classe:
Première
Exercice 1
Déterminer l'ensemble de définition des fonctions suivantes :
1) f : x↦√x(1−x2)
2) g : x↦√1−x2x2+2x
3) h : x↦√1−x+√1x
4) h : x↦x2|2x+1|−2
Exercice 2
Étudier la parité de la fonction f lorsque :
a) f(x)=x3+3x−3
b) f(x)=x25x2−3
c) f(x)=8x3−2x4x5
d) f(x)=x4x2−3
e) f(x)=x√x3+3x
Exercice 3
Étudier le sens de variation des fonctions suivantes :
a) f : x↦(2x+3)2
b) f : x↦−1x
c) f : x↦√x+2
d) f : x↦−5x+3
e) f : x↦1(x−1)2
f) f : x↦|x−1|
Exercice 4
Soit f une fonction périodique, de période 1, telle que :
{si x∈[0;12]:f(x)=xsi x∈[12; 1]:f(x)=−x+1
Faire la représentation graphique de f pour x∈[−4; 5].
Exercice 5
Soit la fonction f représentée graphiquement ci-dessous :
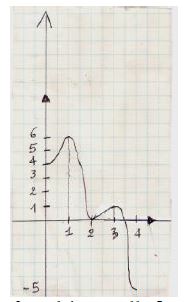
1) Dresser le tableau de variation de f sur l'intervalle [0; 4].
2) Déterminer les extremums relatifs de f.
3) f est-elle monotone sur [0; 2] ? Justifier.
4) Résoudre graphiquement l'équation : f(x)=0.
5) Résoudre graphiquement les inéquations :
a) f(x)≤4b) f(x)≥0
Exercice 6
Soit f et g les fonctions définies par :
f(x)=2x+1x−3 et g(x)=3x+1x−2.
1) Préciser le domaine de définition des fonctions :
f∘g; g∘f; f∘f et g∘g.
2) Calculer :
(f∘g)(x); (g∘f)(x); (f∘f)(x); (g∘g)(x).
Exercice 7
On considère le polynôme Q(x) suivant :
Q(x)=(m3−m2−6m)x3−(m2+m−2)x2+(m−1)x+2m−1.
Déterminer m pour que :
a) deg(Q)=3b) deg(Q)=2c) deg(Q)=1.
Exercice 8
1) Déterminer un polynôme P de degré 3 vérifiant la relation :
P(x)−P(x−1)=x2+x
2) En déduire l'expression en fonction de n de la somme :
S=(1×2)+(2×3)+(3×4)+⋯n(n+1)
Exercice 9
Soit P(x)=x4+2x3−16x2−2x+15
1) Montrer que 1 et -1 sont racines de P(x) puis donner une factorisation de P(x).
2) Résoudre l'équation P(x)=0 et l'inéquation P(x)≤0.
Conseil : Ne pas passer plus de 20 minutes sur un seul exercice.
Durée 3h
Commentaires
Anonyme (non vérifié)
ven, 11/19/2021 - 23:55
Permalien
Téléchargement
Anonyme (non vérifié)
ven, 11/19/2021 - 23:55
Permalien
Téléchargement
Ajouter un commentaire